La sezione aurea La sezione aurea A C



























































- Slides: 75

La sezione aurea


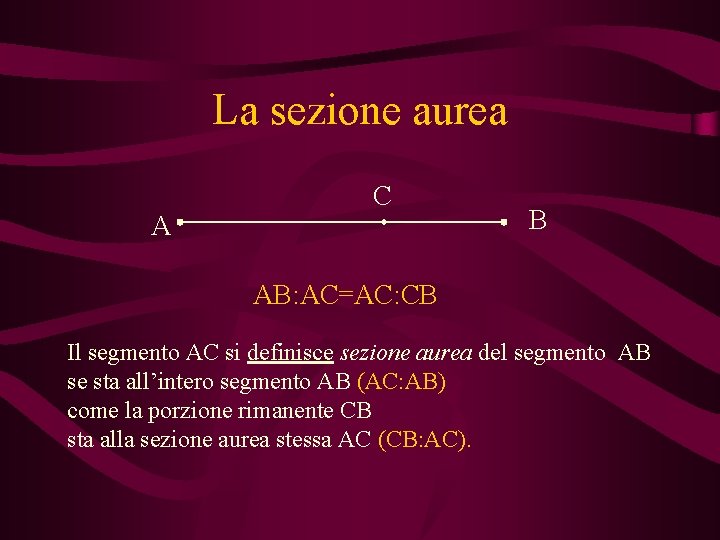
La sezione aurea A C B AB: AC=AC: CB Il segmento AC si definisce sezione aurea del segmento AB se sta all’intero segmento AB (AC: AB) come la porzione rimanente CB sta alla sezione aurea stessa AC (CB: AC).


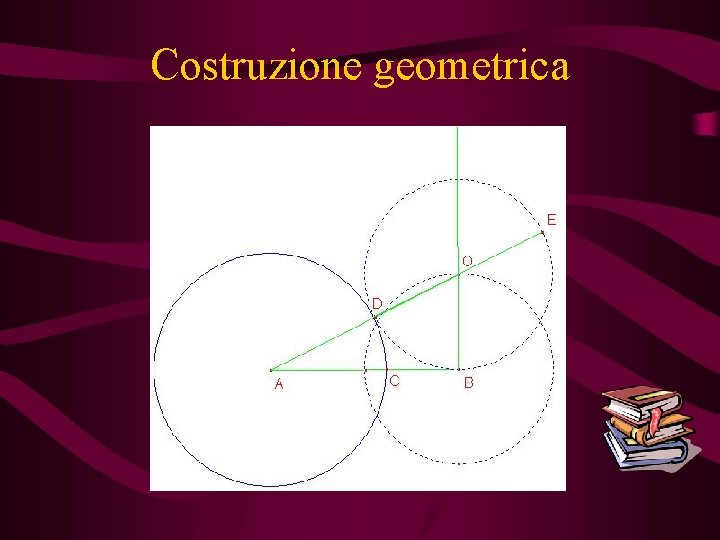
Costruzione geometrica

Dimostrazione della costruzione geometrica Per il teorema della secante e della tangente si ha: AB : AD = AE : AB Da cui scomponendo si ottiene: (AB – AD) : AD = (AE – AB) : AB Dato che: AB – AD = AB - AC = CB AE – AB = AE – CD =AD Perciò l’ultima proporzione diventa: CB : AD = AD : AB Da cui : AB : AC = AC : CB

Misura della sezione aurea a A A B C x a-x B

Misura della sezione aurea Una sola radice è positiva: x=a*0, 618…. OSSERVAZIONI: La lunghezza del segmento e la sua sezione aurea sono incommensurabili.

Rapporto aureo AB/AC

F con 454 cifre decimali 1. 618033 9887498 9484820 4586834 3656381 1772030 9179805 7628621 3544862 2705260 4628189 0244970 7207204 1893911 3748475 4088075 3868917 5212663 3862223 5369317 9318006 0766726 3544333 8908659 5939582 9056383 2266131 9928290 2678806 7520876 6892501 7116962 0703222 1043216 2695486 2629631 3614438 1497587 0122034 0805887 9544547 4924618 5695364 8644492 4104432 0771344 9470495 6584678 8509874 3394422 1254487 7066478 0915884 6074998 8712400 7652170 5751797 8834166 2562494 0758906 9704000 2812104 2762177 1117778 0531531

Alcune osservazioni

Altri modi di vedere il rapporto aureo

Come frazione continua…. .


La successione di Fibonacci Il matematico pisano Leonardo Fibonacci viene ricordato soprattutto per via della sua sequenza divenuta ormai celeberrima. (La sequenza di Fibonacci risale all’anno 1202. ) Essa si compone di una successione di numeri nella quale ognuno di essi è la somma dei due numeri precedenti 0 0+1= 1+1= 2+3= 3+5= 1 1 2 3 5 8 5+8= 13 8+13= 21 13+21= 34 21+34= 55 34+55= 89 55+89= 144 …

La successione di Fibonacci Johannes Kepler notò che facendo il rapporto fra due numeri di Fibonacci consecutivi, esso si avvicinava sempre più a 1, 61803, valore noto anche con il nome di rapporto aureo. 2/1=2 3/2=1, 5 5/3=1, 666 8/5=1, 6 13/8=1, 625

Il rettangolo aureo Esiste uno speciale rettangolo le cui dimensioni corrispondono alla lunghezza di un segmento ed alla sua sezione aurea. Il suo nome è rettangolo aureo.

Il rettangolo aureo Anche il rettangolo CBDF è un rettangolo aureo Così come lo è il rettangolo FDGH…

Rettangolo aureo e Fibonacci


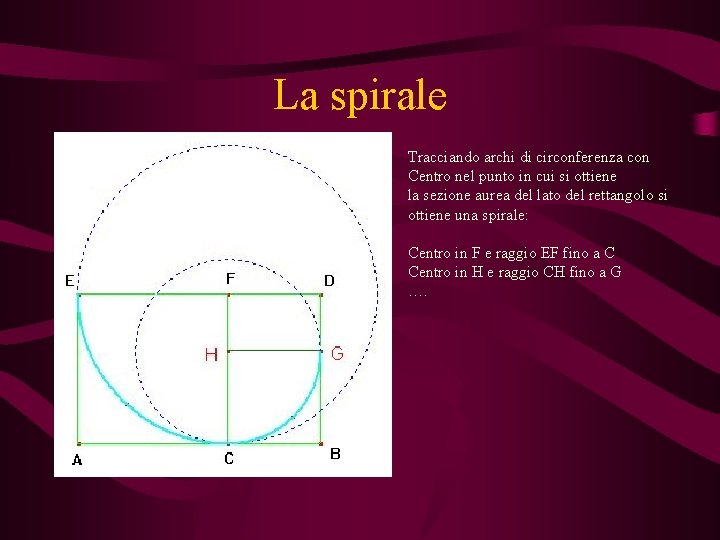
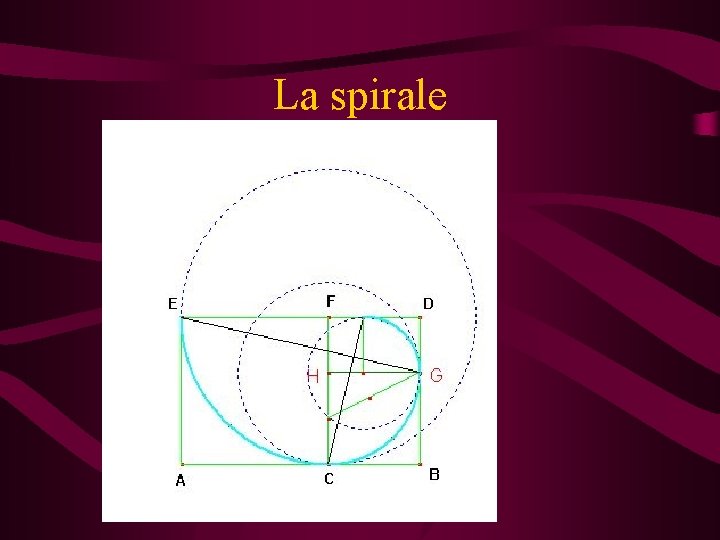
La spirale Tracciando archi di circonferenza con Centro nel punto in cui si ottiene la sezione aurea del lato del rettangolo si ottiene una spirale: Centro in F e raggio EF fino a C Centro in H e raggio CH fino a G ….

La spirale

Spirale aurea Di quali proprietà gode questa spirale?

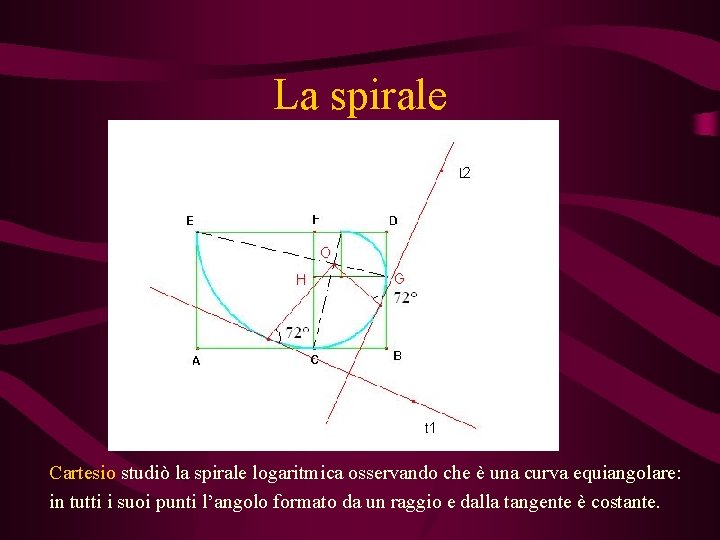
La spirale Cartesio studiò la spirale logaritmica osservando che è una curva equiangolare: in tutti i suoi punti l’angolo formato da un raggio e dalla tangente è costante.


Sulla testa di un girasole il numero delle spirali rientra spesso in questo schema: 89 spirali che si irradiano ripide in senso orario, 55 che si muovono in senso antiorario e 34 che si muovono in senso orario ma meno ripido. Il più grande girasole mai visto aveva 144, 89 e 55 spirali.


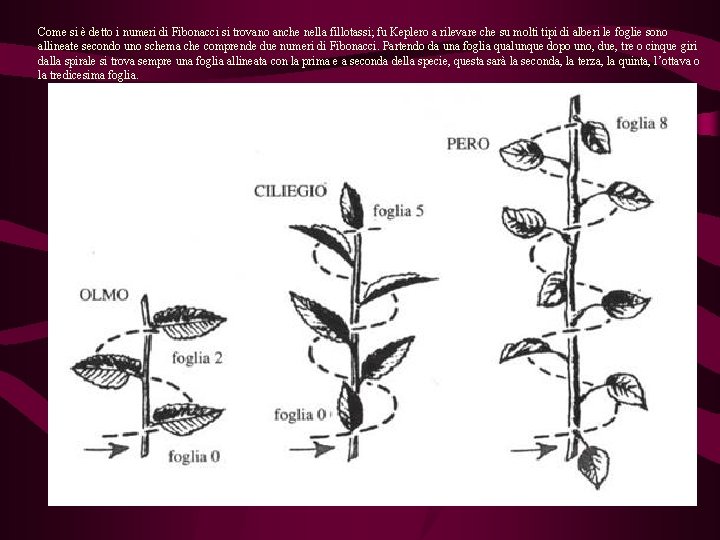
Come si è detto i numeri di Fibonacci si trovano anche nella fillotassi; fu Keplero a rilevare che su molti tipi di alberi le foglie sono allineate secondo uno schema che comprende due numeri di Fibonacci. Partendo da una foglia qualunque dopo uno, due, tre o cinque giri dalla spirale si trova sempre una foglia allineata con la prima e a seconda della specie, questa sarà la seconda, la terza, la quinta, l’ottava o la tredicesima foglia.








LA GENESI DELLE GALASSIE A SPIRALE Le prime teorie consideravano i bracci di spirale alla stregua di strutture connesse al disco centrale: eiezioni di materia del nucleo galattico, aventi differente luminosità ed estensione. Ogni galassia spirale ha un movimento rotatorio non uniforme : le regioni centrali, infatti, hanno una velocità di rotazione più alta delle periferiche. Il fenomeno della rotazione differenziale, nella quale le zone esterne hanno una velocità angolare più lenta rispetto a quelle interne, fece sorgere tra gli scienziati il dubbio che nel tempo i bracci più vicini al disco nel tempo si sarebbero avvolti su se stessi, scomparendo definitivamente. A tal risoluzione, nel 1941 fu proposta una teoria che scinde i bracci di spirale dalla cinematica della galassia: è la teoria delle onde di densità, comparabili ad onde di compressione, come le onde sonore che si propagano nell’atmosfera terrestre. Essa prevede che i bracci a spirale si formino dall’interazione tra onde di densità e materia galattica. Qual è il meccanismo che interessa il fenomeno? Si tenga presente che la materia del disco galattico si muove in rotazione differenziale, mentre l’onda di densità si muove a velocità angolare costante, nello stesso senso della materia del disco. Quando la materia del disco, più veloce dell’onda, raggiunge l’onda stessa, essa altera la propria velocità, rallentando comprimendosi. Successivamente la materia abbandona l’onda, riacquistando velocità e densità. Con l’alternarsi d’interazioni successive, il raggio di curvatura va dunque continuamente aumentando: una linea ipotetica che parte dall’origine diminuisce gradualmente il suo profilo arcuato mano che si allontana da centro. Si delinea così la caratteristica struttura a girandola delle spirali galattiche. L’onda d’urto, che investe il gas interstellare, provoca la formazione di nuove stelle: le più massicce e luminose vivono il tempo necessario per attraversare il braccio a spirale (circa 10 milioni d’anni) rendendolo quindi luminoso.

Un po’ di storia… Ippaso da Metaponto (V sec a. C. ) Euclide (III sec. a. C. ) Tolomeo (100 -179 d. C. ) Luca Pacioli (1496) Keplero (1571 -1630)

La sezione aurea Keplero affermava che: “La geometria possiede due grandi tesori: uno è il teorema di Pitagora; l’altro la divisione di una linea secondo il rapporto estremo e medio. Possiamo paragonare il primo a una certa quantità d’oro, e definire il secondo una pietra preziosa”.

La spirale logaritmica • Torricelli calcolò la lunghezza di tale curva. • Bernouilli dimostrò parecchie proprietà della spirale: l’evoluta di una spirale logaritmica è una spirale logaritmica stessa (simillima filia matri). (Volle che sulla sua tomba fosse incisa una spirale log) • La curva ottenuta con l’operazione di inversione è una spirale uguale a quella di partenza. • Problema dei quattro cani: la curva pur avendo lunghezza finita (pari al lato del quadrato) è illimitata – i cani per raggiungersi devono compiere infiniti giri – simile al paradosso di Zenone su Achille e la tartaruga. • L’equazione in coordinate polari è : r=aet cota con a l’angolo costante formato dalla tangente e dal raggio.

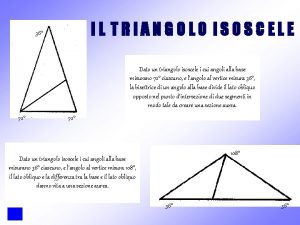
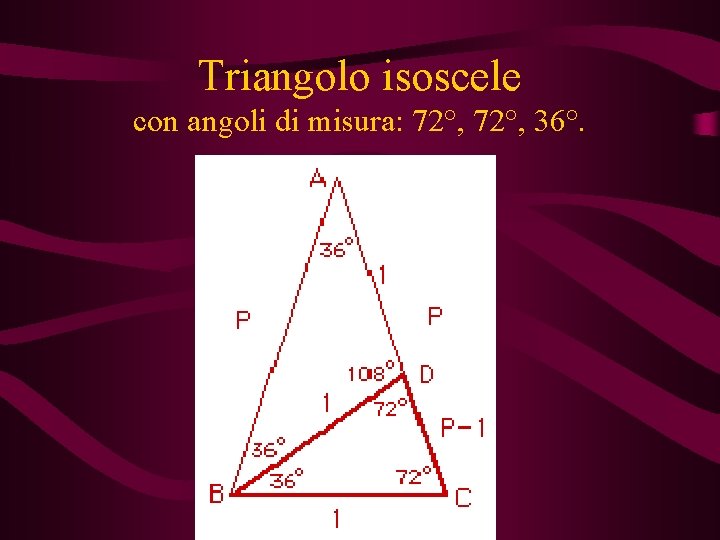
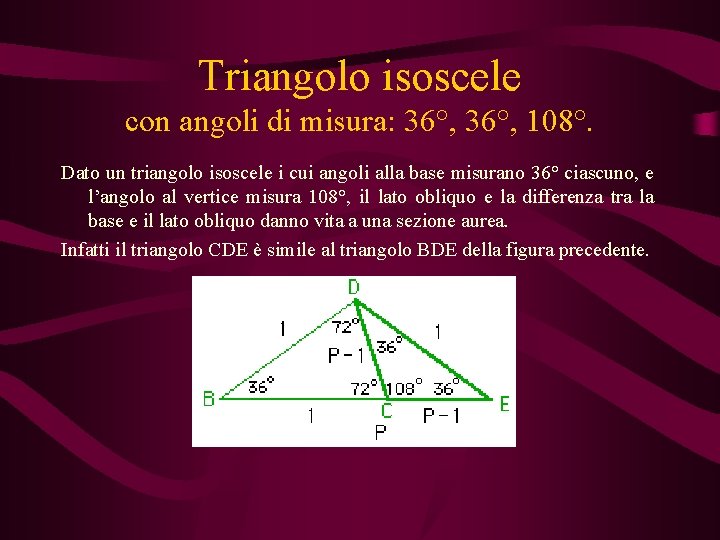
Triangolo isoscele con angoli di misura: 72°, 36°.

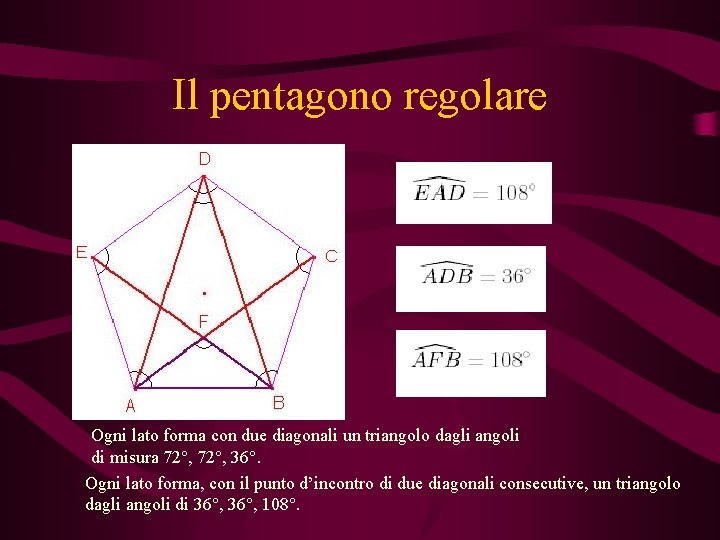
Il pentagono regolare Ogni lato forma con due diagonali un triangolo dagli angoli di misura 72°, 36°. Ogni lato forma, con il punto d’incontro di due diagonali consecutive, un triangolo dagli angoli di 36°, 108°.

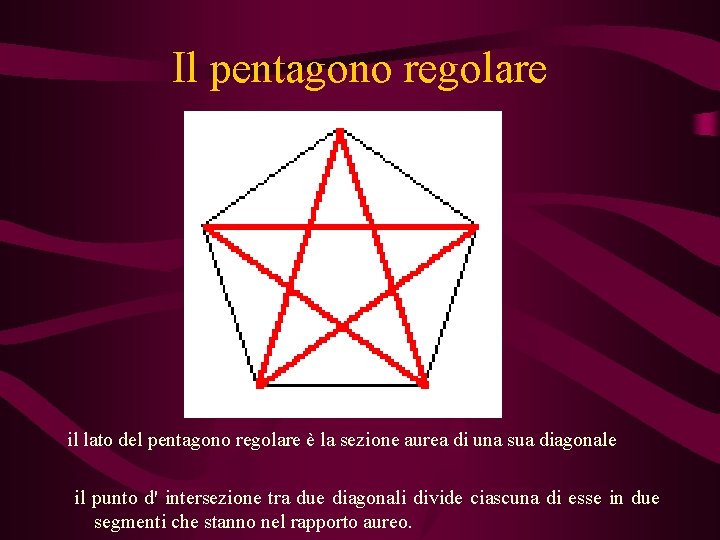
Il pentagono regolare il lato del pentagono regolare è la sezione aurea di una sua diagonale il punto d' intersezione tra due diagonali divide ciascuna di esse in due segmenti che stanno nel rapporto aureo.

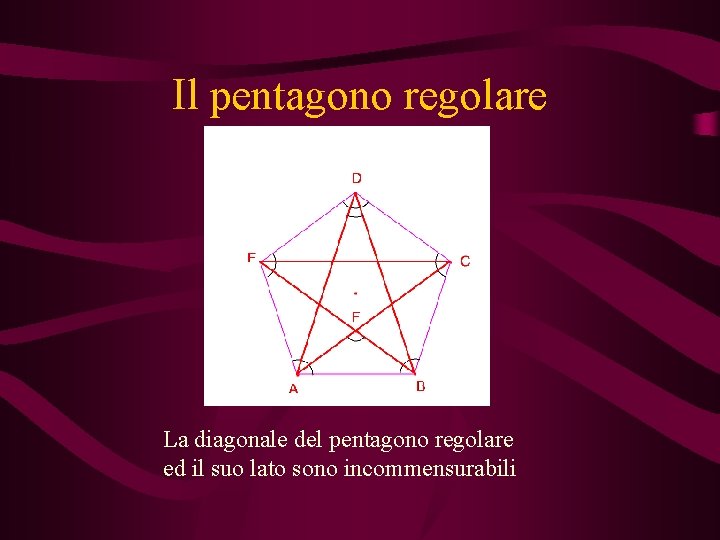
Il pentagono regolare La diagonale del pentagono regolare ed il suo lato sono incommensurabili

Triangolo isoscele con angoli di misura: 36°, 108°. Dato un triangolo isoscele i cui angoli alla base misurano 36° ciascuno, e l’angolo al vertice misura 108°, il lato obliquo e la differenza tra la base e il lato obliquo danno vita a una sezione aurea. Infatti il triangolo CDE è simile al triangolo BDE della figura precedente.

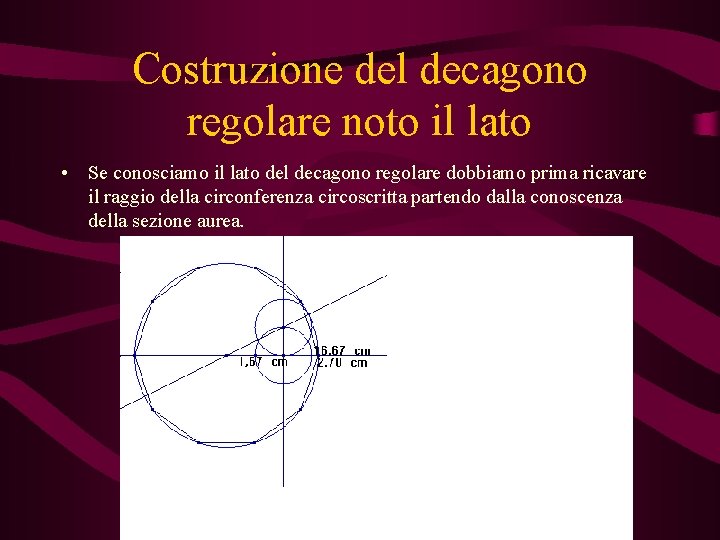
Costruzione del decagono regolare Il lato del decagono regolare è pari alla sezione aurea del raggio della circonferenza circoscritta:

Costruzione del decagono regolare noto il lato • Se conosciamo il lato del decagono regolare dobbiamo prima ricavare il raggio della circonferenza circoscritta partendo dalla conoscenza della sezione aurea.



La sezione aurea e l’aritmetica b) Aritmetica In questa sezione si verifica la relazione tra la successione di Fibonacci e il rapporto aureo e si presentano alcune applicazioni in campi diversi dell'aritmetica. c) Botanica e Zoologia In questa sezione si presentano alcuni esempi di come in natura si ritrovi la successione di Fibonacci.

Somma di numeri di Fibonacci Consideriamo la serie di Fibonacci A, B, C, D, E, G. . . Se si sommano due o più numeri consecutivi di tale serie, sempre a partire da A, e si aggiunge ulteriormente "1", si ottiene sempre un altro numero di Fibonacci che nella sequenza segue di due posti l'ultimo termine della somma ( A+B+C+1 = E ) • Esempi: 1+1+2+3+5+1 = 13 In questo caso si sono sommati i primi cinque numeri di Fibonacci, si è aggiunto uno e si è ottenuto il settimo numero della sequenza. 1+1+2+3+5+8+13+21+34+55+89+1=233 In questo caso invece si sono sommati i primi undici numeri di Fibonacci, si è aggiunto uno e si è ottenuto il tredicesimo numero della sequenza. Inoltre se si prendono due numeri di Fibonacci consecutivi e se ne fa il quadrato, la somma fra i quadrati è un altro numero di Fibonacci che nella sequenza occupa il posto risultante dalla somma delle posizioni dei due termini di partenza. • Esempi: 32+52=34 In questo caso si sono presi il quarto e il quinto numero della sequenza, se ne è fatto il quadrato e la somma fra i quadrati è risultata essere il nono numero di Fibonacci. 82+132= 233 In questo caso si sono presi il sesto e il settimo numero della sequenza e la somma fra i loro quadrati ha dato il tredicesimo numero di Fibonacci.

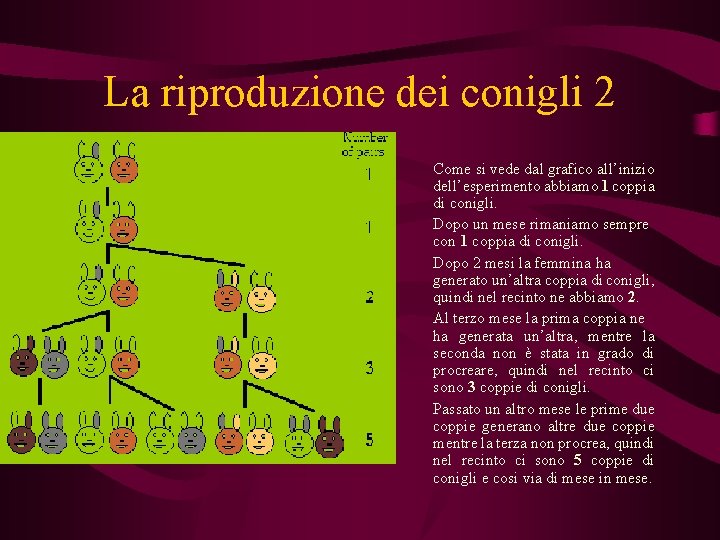
Zoologia: la riproduzione dei conigli In condizioni ideali una coppia di conigli è in grado di riprodursi già da un mese dopo la nascita. La femmina è in grado di generare una seconda coppia di conigli già un mese dopo l’accoppiamento con il maschio. Prendiamo una coppia di conigli e mettiamola in un recinto. Supponiamo che i nostri conigli non muoiano mai.

La riproduzione dei conigli 2 Come si vede dal grafico all’inizio dell’esperimento abbiamo 1 coppia di conigli. Dopo un mese rimaniamo sempre con 1 coppia di conigli. Dopo 2 mesi la femmina ha generato un’altra coppia di conigli, quindi nel recinto ne abbiamo 2. Al terzo mese la prima coppia ne ha generata un’altra, mentre la seconda non è stata in grado di procreare, quindi nel recinto ci sono 3 coppie di conigli. Passato un altro mese le prime due coppie generano altre due coppie mentre la terza non procrea, quindi nel recinto ci sono 5 coppie di conigli e cosi via di mese in mese.

La riproduzione dei conigli 3 Schema della crescita delle famiglie di conigli Botanica

Zoologia: l’albero genealogico dei fuchi • • L'albero genealogico di un fuco presenta chiaramente la sequenza di Fibonacci. Bisogna innanzitutto dire che in uno sciame non tutte le api sono uguali: ci sono innanzitutto le api (femmine) e i fuchi (maschi). Le femmine sono tutte generate dall’unione dell’ape regina con un fuco e si dividono in operaie e regine. Le api regine sono api operaie nutrite con pappa reale ma, diversamente dalle operaie, sono in grado di produrre uova. I maschi nascono dalle uova dell ape regina. Quindi possiamo dire che le femmine hanno 2 genitori: l’ape regina e un fuco, mentre i fuchi hanno un solo genitore: l’ape regina. Prendiamo in esame l’albero genealogico di un fuco. 1 fuco ha 1 genitore che ha sua volta ha 2 genitori che a loro volta hanno 3 genitori che a loro volta hanno 5 genitori e così via.

Zoologia: le spirali delle conchiglie In natura molte conchiglie hanno una forma a spirale logaritmica. Ne è un esempio il nautilus di figura

Ancora una spirale logaritmica

Botanica La sequenza di Fibonacci si trova in molte piante e fiori. Ne è un esempio l’Achillea ptarmica. La crescita di questa pianta segue questo schema qui sopra disegnato. Ogni ramo impiega un mese prima di potersi biforcare. Al primo mese quindi abbiamo 1 ramo, al secondo ne abbiamo 2, al terzo 3, al quarto 5 e così via.

La sezione aurea e l’arte Architettura Antica e Rinascimentale In questa sezione si presentano esempi nell'architettura egiziana, greca, romana e rinascimentale in cui si utilizza il modulo del rettangolo aureo. Scultura In questa sezione si presentano alcuni esempi nella scultura egizia e greca in cui si utilizza il modulo del rettangolo aureo. Pittura In questa sezione si presentano esempi di utilizzo del rapporto aureo e del rettangolo aureo nella pittura rinascimentale e moderna. Musica In questa sezione si presentano esempi di brani che presentano l’uso della sezione aurea per la suddivisione degli intervalli e l’analogia tra la coclea dell’orecchio umano e la spirale logaritmica.

Architettura classica: Il Partenone di Atene Torna al rettangolo aureo

Il portale di Castel del Monte Torna al pentagono

La piramide di Giza

L’uomo vitruviano

La pittura: la sezione aurea e l’arte moderna L’ultima cena (Salvator Dalì)

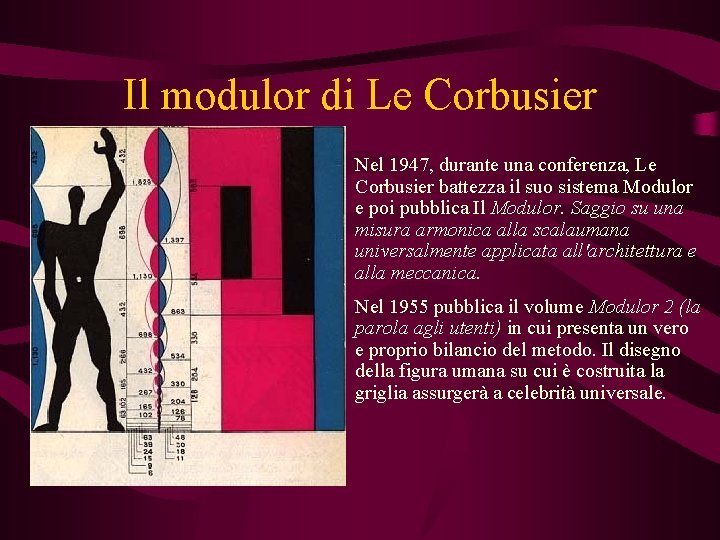
Le Corbusier Nel 1943 Le Corbusier elabora una griglia di misure armoniche per stabilire una serie di grandezze articolate fra loro dalla "sezione aurea" o "numero aureo". Ma, come sempre attento al rapporto con la società , Le Corbusier non aveva costruito una griglia astratta su base puramente matematica, come la serie di numeri armonici stilata da Fibonacci nel XIII secolo: aveva invece ripreso i principi su cui aveva lavorato Matila Ghyka intorno al 1930, e aveva definito la griglia relativamente alle dimensioni principali del corpo umano.

Il modulor di Le Corbusier Nel 1947, durante una conferenza, Le Corbusier battezza il suo sistema Modulor e poi pubblica Il Modulor. Saggio su una misura armonica alla scalaumana universalmente applicata all'architettura e alla meccanica. Nel 1955 pubblica il volume Modulor 2 (la parola agli utenti) in cui presenta un vero e proprio bilancio del metodo. Il disegno della figura umana su cui è costruita la griglia assurgerà a celebrità universale.

Le Corbusier Dopo aver messo a punto il sistema, Le Corbusier regolerà su di esso le misure di tutti gli elementi costitutivi dei suoi progetti. La "grandezza conforme" dell'Unità di abitazione di Marsiglia discende proprio da questo schema di misure proporzionali. Le Corbusier usa infatti il Modulor per definire le misure degli ambienti e degli utensili; a lato, studio del Modulor per diverse azioni comuni.

La musica: I primi elementi della successione di Fibonacci sono: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, … A partire da tale successione, se ne forma una di tipo frazionario, dalla quale emergono i seguenti rapporti: 1/1; 2/1; 3/2; 5/3; 8/5; 13/8; 21/13; 34/21; 55/34, 89/55; 144/89 ecc. i cui valori decimali approssimati sono: 1; 2; 1, 5; 1, 666; 1, 625; 1, 619; 1, 617; 1, 6181; 1, 6180 ecc.

Gli intervalli musicali che corrispondono agli intervalli musicali: unisono=1 ottava=2 quinta=1, 5 sesta maggiore=1, 666 sesta minore=1, 6 in cui gli ultimi sono complementari degli intervalli di terza minore e maggiore. se poi applichiamo la serie di Fibonacci alle sovrarmoniche e alle sottoarmoniche di un suono di riferimento(ad es. il DO) avremo che i numeri in successione aurea 3, 5, e 8 superiori al suono dato corrispondono ai suoni MI, SOL e Do acuto e i numeri 3, 5 e 8 inferiori allo stesso suono corrispondono al LAb, FA e DO grave. Abbiamo quindi l'armonia maggiore e minore. (***)

Gli intervalli musicali 2 • Le distanze do-re, re-mi, fa-sol, sol-la, la-si sono ognuna un tono, mentre le distanze mi-fa e si-do sono un semitono. Raggruppando il numero di vibrazioni dei dodici semitoni che si susseguono ricaviamo una proporzione continua: T 1: T 2=T 2: T 3=T 3: T 4 eccetera Possiamo arrivare a dire che il numero delle variazioni che si differenziano per otto semitoni si comporta quindi come la sezione aurea: T 1: T 9=T 9: T 17=1: 1, 618

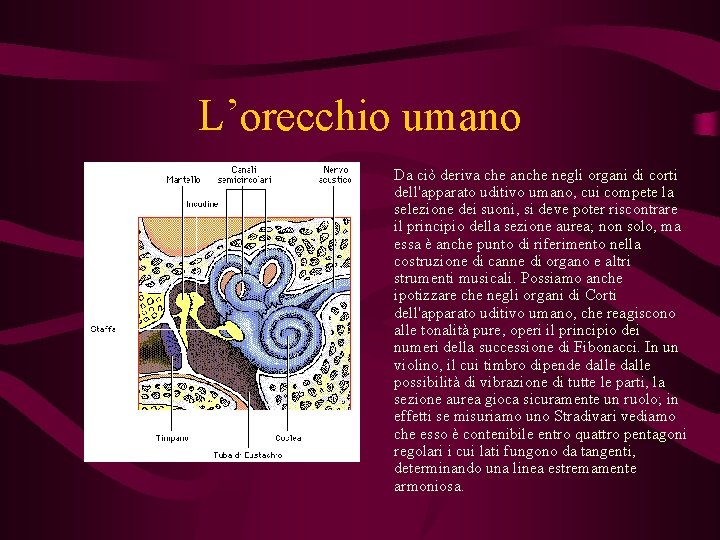
L’orecchio umano Da ciò deriva che anche negli organi di corti dell'apparato uditivo umano, cui compete la selezione dei suoni, si deve poter riscontrare il principio della sezione aurea; non solo, ma essa è anche punto di riferimento nella costruzione di canne di organo e altri strumenti musicali. Possiamo anche ipotizzare che negli organi di Corti dell'apparato uditivo umano, che reagiscono alle tonalità pure, operi il principio dei numeri della successione di Fibonacci. In un violino, il cui timbro dipende dalle possibilità di vibrazione di tutte le parti, la sezione aurea gioca sicuramente un ruolo; in effetti se misuriamo uno Stradivari vediamo che esso è contenibile entro quattro pentagoni regolari i cui lati fungono da tangenti, determinando una linea estremamente armoniosa.

Biografia di Fibonacci • Leonardo Fibonacci, figlio di Guglielmo Bonacci, nacque a Pisa intorno al 1170. Suo padre era segretario della Repubblica di Pisa e responsabile a partire dal 1192 del commercio pisano presso la colonia di Bugia, in Algeria. Alcuni anni dopo il 1192, Bonacci portò suo figlio con lui a Bugia. Il padre voleva che Leonardo divenisse un mercante e così provvedette alla sua istruzione nelle tecniche del calcolo, specialmente quelle che riguardavano le cifre indo-arabiche, che non erano ancora state introdotte in Europa. In seguito Bonacci si assicurò l’aiuto di suo figlio per portare avanti il commercio della repubblica pisana e lo mandò in viaggio in Egitto, Siria, Grecia, Sicilia e Provenza. Leonardo colse l’opportunità offertagli dai suoi viaggi all’estero per studiare e imparare le tecniche matematiche impiegate in queste regioni. Intorno al 1200, Fibonacci tornò a Pisa dove per i seguenti 25 anni lavorò alle sue personali composizioni matematiche.

Biografia di Fibonacci 2 In tutta la sua produzione l’opera più importante è il "Liber abaci", comparso attorno al 1228: è un lavoro contenente quasi tutte le conoscenze aritmetiche e algebriche ed ha avuto una funzione fondamentale nello sviluppo della matematica dell’Europa occidentale. In particolare la numerazione indo-arabica, che prese il posto di quella latina semplificando notevolmente i commerci extraeuropei, fu conosciuta in Europa tramite questo libro. In tale sistema di numerazione, il valore delle cifre dipende dal posto che occupano: pertanto egli fu costretto ad introdurre un nuovo simbolo, corrispondente allo zero "0", per indicare le posizioni vacanti. La reputazione di Leonardo come matematico divenne così grande che l’imperatore Federico II gli chiese un’udienza mentre era Pisa nel 1225. Dopo il 1228 non si sa in sostanza niente della vita di Leonardo tranne il decreto della Repubblica di Pisa che gli conferì il titolo di "Discretus et sapiens magister Leonardo Bigollo" a riconoscimento dei grandi progressi che apportò alla matematica. Fibonacci morì qualche tempo dopo il 1240, presumibilmente a Pisa. Anche al giorno d’oggi la fama di Leonardo è tale che esiste un’intera pubblicazione dedicata a questi argomenti: il "Fibonacci Quarterly", periodico matematico dedicato interamente all’aritmetica connessa alla sequenza di Fibonacci.

Conclusioni • Sono rimasti alcuni problemi aperti, che ci auguriamo possano essere di stimolo per ulteriori approfondimenti. • I numeri di Fibonacci si ritrovano in natura: come mai la natura sceglie il rapporto aureo? • Il rapporto aureo sembra dare alla visione dello spettatore una sensazione di geometrica armonia. Ciò avviene perché lo spettatore è condizionato da canoni estetici e da modelli culturali o c’è qualcosa di più profondo nell’inconscio che ci porta inevitabilmente a preferire certi rapporti? In proposito si può osservare che il rapporto aureo si ritrova anche in civiltà lontane, certamente non condizionate dai modelli culturali occidentali, come per esempio la piramide di Teotiuacan in Messico.

Bibliografia Fare Matematica, Fascicolo n. 1, Geometria e Arte, ed. BCM Maurizio Bonicatti, Enciclopedia di tutte le arti di tutti i popoli in tutti i tempi, vol. II, pp. 41 -51, Fratelli Fabbri Editori, Milano 1974 G. Brigola, Annali della fabbrica del Duomo, Milano 1877, vol I, pp. 209– 211 Giorgio Cricco, Francesco P. Di Teodoro, Itinerario dell’arte, Vol. 1, ed. Zanichelli M. Gaffo, Numeri e cifre (tratto da "Focus" n. 79, Maggio 1999), ed. Mondadori Hans M. Enzensberger, Il mago dei numeri, Einaudi Martin Kemp, La scienza dell’Arte, ed. Giunti Hamilton Luske, Donald in Math. Magic land, Walt Disney Productions, 1987 Carl Schefold, Collana il Marco Polo (vol. Grecia classica, pp. 131 -181) E. Vorobyou, I numeri di Fibonacci, Le Monnier J. Wasserman, Leonardo da Vinci, ed. Garzanti Jonathan D. Kramer, The Time of Music: New Meanings, New Temporalities, New Listening Strategies, Schirmer Books, New York, 1988. Roy Howat, Debussy in proportion: a musical analysis, Cambridge University Press, 1983 (cfr. anche: Review-article: Bartók, Lendvai and the principles of proportional analysis, in «Music Analysis» , 2: 1/1983, pp. 69 -95). Roger Herz-Fischler, A Mathematical History of the Golden Number, Dover, N. Y. 1998. Helmut Reis, Der Goldene Schnitt und seine Bedeutung für die Harmonik, ORPHEUS - Schriftenreihe zu Grundfragen der Musik, herausgegeben von Martin Vogel, Bd. 54, Verlag für systematische Musikwissenschaft Gmb. H, Bonn 1990. Giuseppina Masotti Biggiogero, Luca Pacioli e la sua “Divina proportione”, in: «Istituto Lombardo (Rend. Sc. )» , A 94, 1960, pp. 3 -30.

La sezione aurea e la geometria In questa sezione si presentano la definizione di sezione aurea e alcune costruzioni geometriche significative della relazione tra la sezione aurea e i poligoni regolari.
 Sequenza fibonacci
Sequenza fibonacci Spirale aurea costruzione
Spirale aurea costruzione Spirale di fibonacci
Spirale di fibonacci Annunciazione leonardo sezione aurea
Annunciazione leonardo sezione aurea Partenone sezione aurea
Partenone sezione aurea Sezione aurea terapeutica
Sezione aurea terapeutica Immagini di un triangolo isoscele
Immagini di un triangolo isoscele Fotosintesi clorofilliana formula
Fotosintesi clorofilliana formula Disegni pezzi meccanici
Disegni pezzi meccanici Diffusione thomson
Diffusione thomson Sezione durto
Sezione durto Sezione di gola
Sezione di gola Cos'è il sarcomero
Cos'è il sarcomero Struttura longitudinale della nave
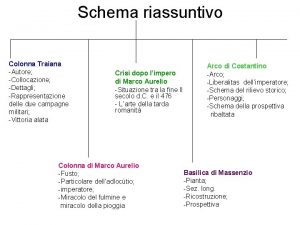
Struttura longitudinale della nave Colonna aureliana e traiana
Colonna aureliana e traiana Ossatura nave
Ossatura nave Evoluta metacentrica
Evoluta metacentrica Tecnica parker kerr
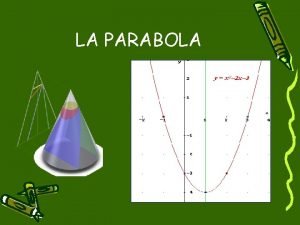
Tecnica parker kerr Sezione conica
Sezione conica Sezioni tronco encefalico
Sezioni tronco encefalico Cai sezione di castelli te
Cai sezione di castelli te Sezione polizia stradale ancona
Sezione polizia stradale ancona Anthyllis aurea
Anthyllis aurea Arcadismo fugere urbem
Arcadismo fugere urbem Clathrina aurea
Clathrina aurea Selection pressure
Selection pressure El partenon proporcion aurea
El partenon proporcion aurea Mai fare agli altri ciò che non vorresti fosse fatto te
Mai fare agli altri ciò che non vorresti fosse fatto te Proporcion aurea partenon
Proporcion aurea partenon Statua di nerone
Statua di nerone 1,61803
1,61803 Domus romana palazzo valentini
Domus romana palazzo valentini Stabilizing selection
Stabilizing selection Chopos definicion
Chopos definicion Partenon proporcion aurea
Partenon proporcion aurea Tratta gli altri come vorresti essere trattato
Tratta gli altri come vorresti essere trattato Propiedades generales de la materia
Propiedades generales de la materia Taphrina kruchii
Taphrina kruchii