La Regla de la Cadena Tomado de UNIMET








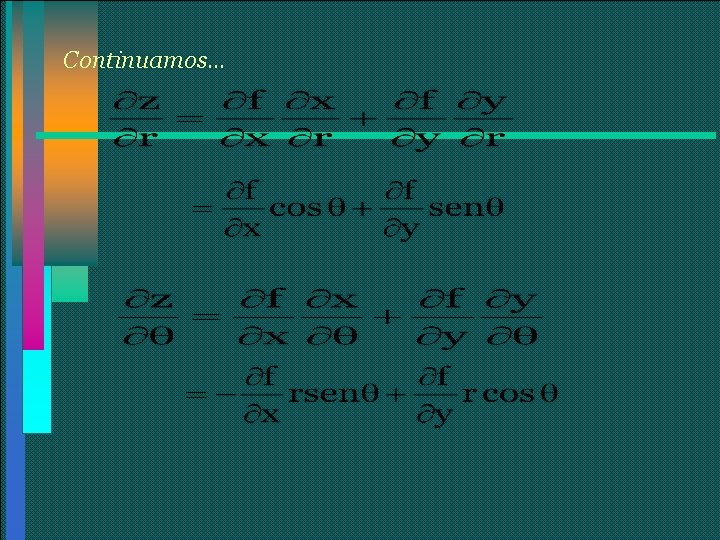
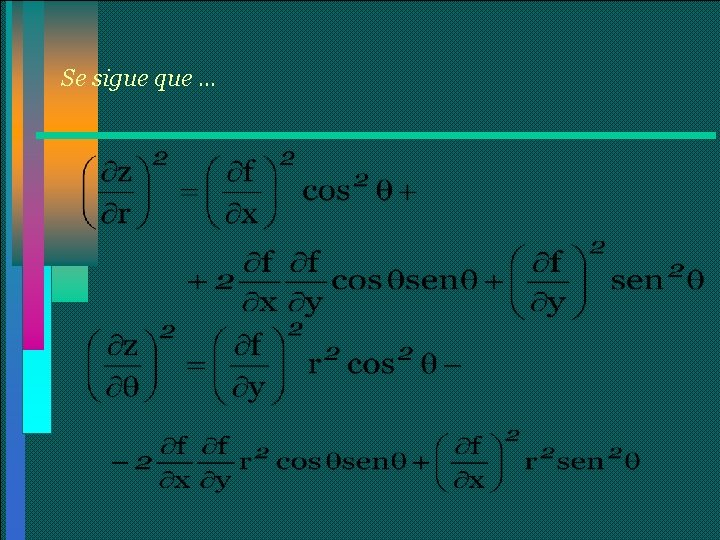




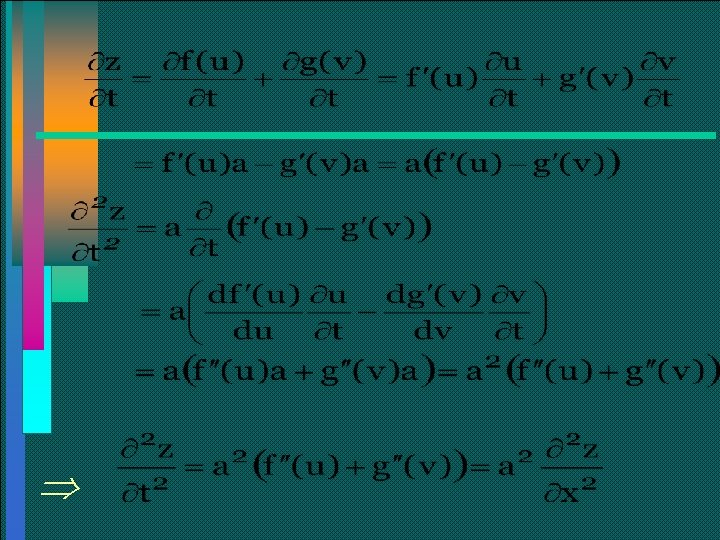














- Slides: 35

La Regla de la Cadena Tomado de UNIMET Prof. Antonio Syers

Introducción Recordemos que la regla de la cadena para una función y = f(x) ; y x = g(t), ambas funciones derivables, entonces y es una función derivable con respecto a t y se cumple: Para funciones de varias variables, la regla de la cadena tiene varias versiones:

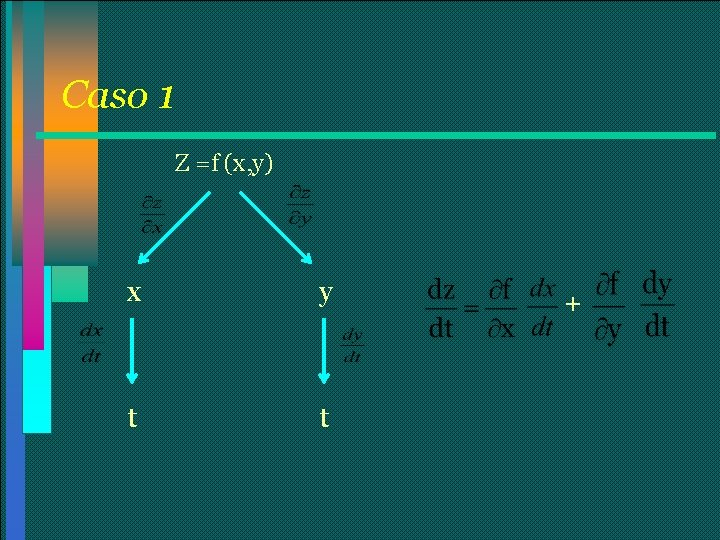
Caso 1 Supongamos que z = f(x, y) es una función diferenciable de x y de y, donde x=g(t) y y=h(t) son funciones derivables de t ; entonces z es una función derivable de t y se cumple que: Veamos esta fórmula de manera gráfica:

Caso 1 Z =f (x, y) x y t t +

Ejemplo Si en el punto (x, y) y representa la temperatura Son las ecuaciones paramétricas de una curva C , calcule la razón de cambio de la temperatura T a lo largo de la curva x t y t T +

Continuamos… Si queremos saber cual es la razón de cambio de T cuando t = 0, entonces

Caso 1 ( General) Suponga que z es una función derivable de las n variables x 1 , x 2 , x 3 , …, xn , en donde cada xj es una función de t. Por consiguiente z es una función derivable de t y se cumple:

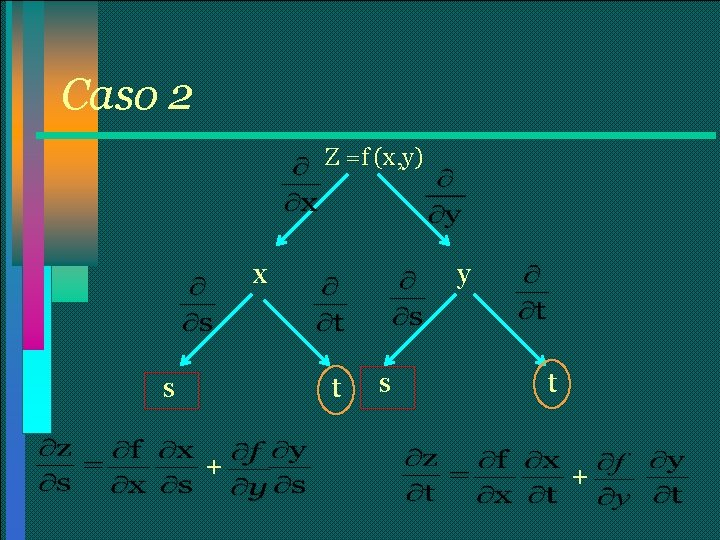
Caso 2 Supongamos que z = f(x, y) es una función derivable de x y de y, donde x = g(s, t), y =h(s, t) y las derivadas parciales de g y h existen. Entonces:

Caso 2 Z =f (x, y) x s y t + s t +

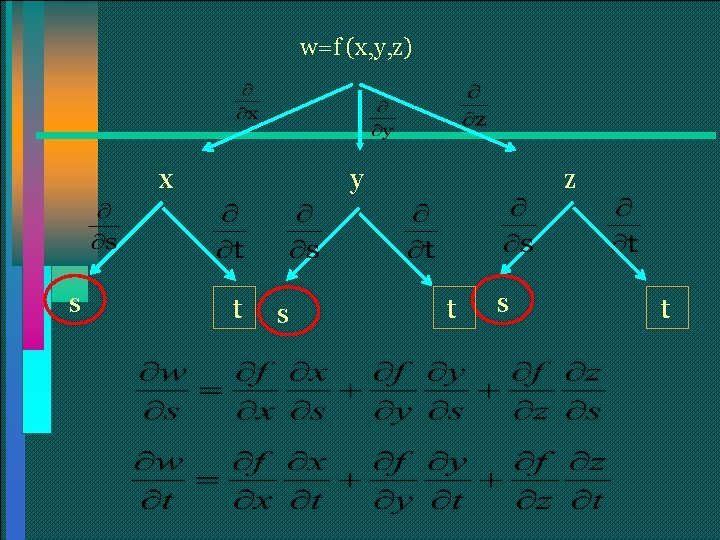
Supongamos que w = f(x, y, z) es una función derivable de x, y , z, donde x = g(s, t), y =h(s, t), z =k(s, t) y las derivadas parciales de g, h, k existen. Entonces

w=f (x, y, z) x s y t s z t s t

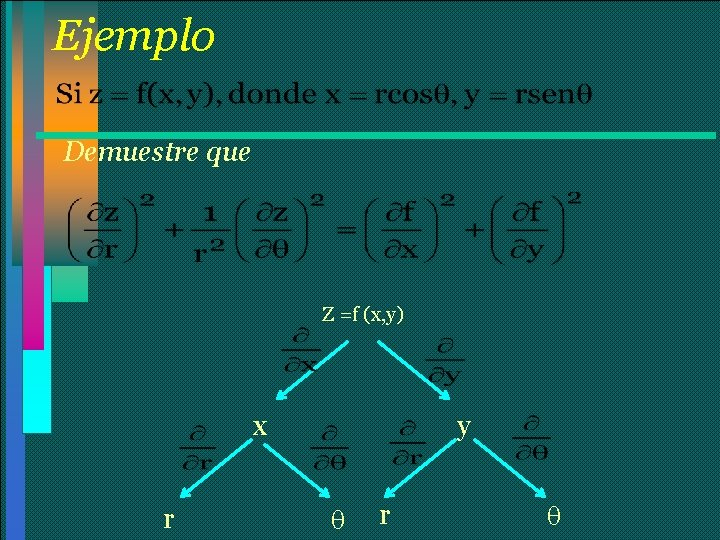
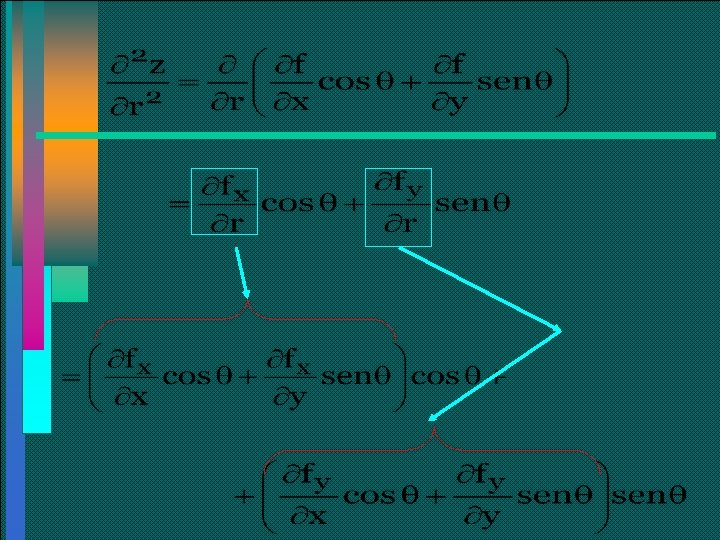
Ejemplo Demuestre que Z =f (x, y) x r y r
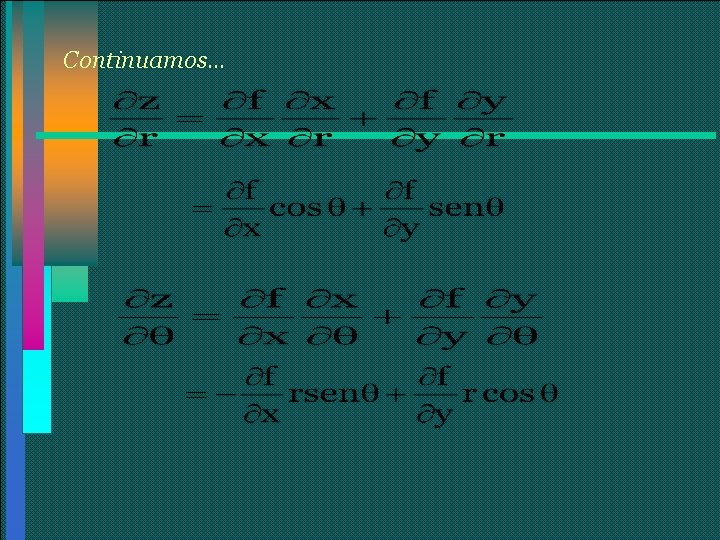
Continuamos…
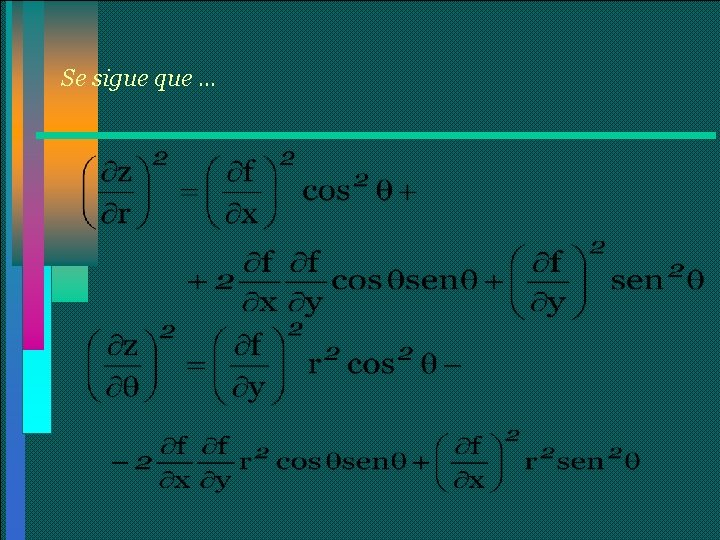
Se sigue que …

Por lo tanto

Segunda derivada La segunda derivada de una función es análoga a la primera, es decir, depende de las mismas variables que depende la función original. Por ejemplo, supongamos que z = f(x, y) es una función derivable de x y de y, donde x = g(s, t), y=h(s, t). Entonces la función derivada fx(x, y) también depende de x y de y, y además x, y dependen de s y t ( esto también se cumple para fy(x, y)). Veamos el siguiente ejemplo:

Ejemplo… Muestre que cualquier función de la forma Donde a es una constante, cumple con la ecuación: Solución: Sea u = x + at, v = x – at, ; entonces

Calculemos ahora
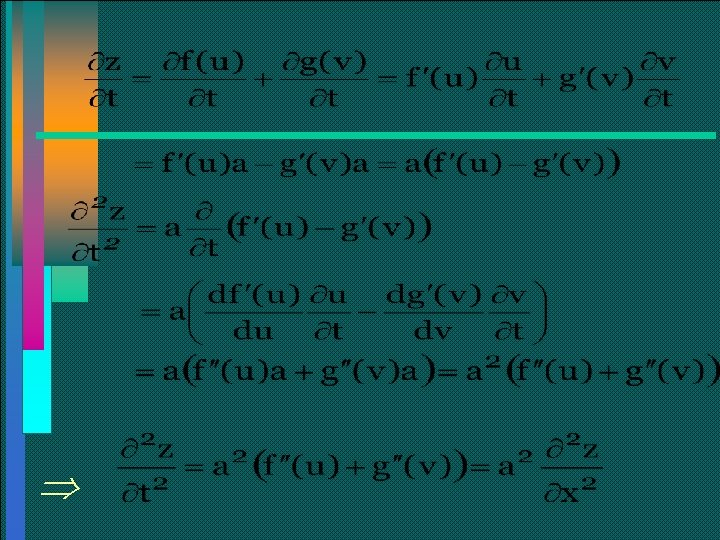

Ejemplo Demuestre que: Solución: Del ejemplo anterior, tenemos que


Por otra parte,


Simplificando resulta, Así, COMPRUEBELO!!

Ecuación de Laplace Definición: Sea f una función, f: IRn IR, diferenciable, se define el Laplaciano de f Y se denomina la ecuación de Laplace a:

Ejemplo Supongamos f(x, y) satisface la ecuación de laplace, esto es, Demuestre que la función z= f(x – 2 y, 2 x + y), también satisface la ecuación de laplace. Demostración: Lo queremos probar es que:

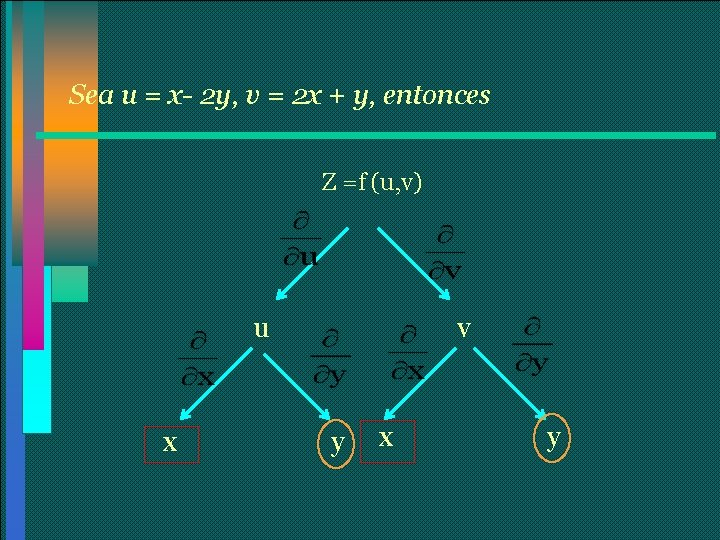
Sea u = x- 2 y, v = 2 x + y, entonces Z =f (u, v) u x v y x y



Entonces, Ecuación de Laplace para f

Derivación Implícita Supongamos que una ecuación de la forma F(x, y) = 0 define a y de manera implícita como una función de x, esto es y = f(x), para todo x en el dominio de f(x). Si F es diferenciable podemos calcular dy/dx. En efecto: Tenemos la ecuación

Supongamos que una ecuación de la forma F(x, y, z) = 0 define a z de manera implícita como una función de x y de y, entonces si F es diferenciable podemos calcular z/ x, z/ y.

Supongamos queremos calcular z/ x

Ejercicio: Supongamos que una ecuación de la forma F(x, y, z) = 0 define a z de manera implícita como una función de x y de y. Demuestre que:

Ejemplo Supongamos que una ecuación de la forma F(xy, z/y) = 0 define a z de manera implícita como una función de x y de y, esto es z=f(x, y). Calcular z/ x. Solución: Sean u=xy , v = z/y
 Regla de la cadena en varias variables
Regla de la cadena en varias variables Qual frase abaixo não apresenta ambiguidade:
Qual frase abaixo não apresenta ambiguidade: Chac mool recursos literarios
Chac mool recursos literarios Casa tomado
Casa tomado Trama alimentaria
Trama alimentaria La cadena de abastecimiento
La cadena de abastecimiento Tasa de prevalencia fórmula
Tasa de prevalencia fórmula Alquinos de cadena abierta
Alquinos de cadena abierta Relacion entre seres vivos
Relacion entre seres vivos Componentes de la cadena epidemiológica
Componentes de la cadena epidemiológica Cadena de valor de la yerba mate
Cadena de valor de la yerba mate Generacion de valor publico
Generacion de valor publico Isomeros de cadena
Isomeros de cadena Los ciclos biogeoquimicos
Los ciclos biogeoquimicos Cadena de aminoácidos
Cadena de aminoácidos Plano monadico
Plano monadico Reacción en cadena de la polimerasa
Reacción en cadena de la polimerasa Ley de logaritmos
Ley de logaritmos Característica del signo lingüístico
Característica del signo lingüístico Rosental cadena dar
Rosental cadena dar Concepto de isomeria
Concepto de isomeria Cadena de sonrisas cuento
Cadena de sonrisas cuento Cadena respiratoria ciclo de krebs
Cadena respiratoria ciclo de krebs Cadena productiva del pan
Cadena productiva del pan Nombre los siguientes alquenos
Nombre los siguientes alquenos Cadena trofica de la taiga
Cadena trofica de la taiga Modelo de la historia natural de la enfermedad
Modelo de la historia natural de la enfermedad Olga lucia giraldo
Olga lucia giraldo Modelo de servucción ejemplos
Modelo de servucción ejemplos Cadena de abastecimiento
Cadena de abastecimiento Cadena alimenticia
Cadena alimenticia Cadena epidemiologica de la brucelosis
Cadena epidemiologica de la brucelosis Q
Q Cadena de valor de la yerba mate
Cadena de valor de la yerba mate Lanzaderas malato aspartato y glicerol 3 fosfato
Lanzaderas malato aspartato y glicerol 3 fosfato Cadena epidemiologica de la fiebre amarilla
Cadena epidemiologica de la fiebre amarilla