La programmation dynamique Le chemin optimal Notations Dsignons

La programmation dynamique

Le chemin optimal • Notations : – Désignons par V ( x ) l’ensemble des taches à accomplir dans un projet, – Soit C ( x , y ) le cout nécessaire pour réaliser une tache et passer à la deuxième, y V( x ) – Soit f ( x ) le chemin optimal pour réaliser toutes les taches entre x et F. • f ( x ) = min C ( x , y ) + f ( y ) et f ( F ) = 0 f( D ) = 11 + f ( F ) f( E ) = 38 + f ( F ) f( B ) = min{ 9 + f ( D ) , 15 + f ( E ) } f( C ) = min{ 37 + f ( D ) , 12 + f ( E ) } f( A ) = min{ 40 + f ( B ) , 13 + f ( C ) } 40 9 B D 11 15 A F 37 13 C 38 12 E

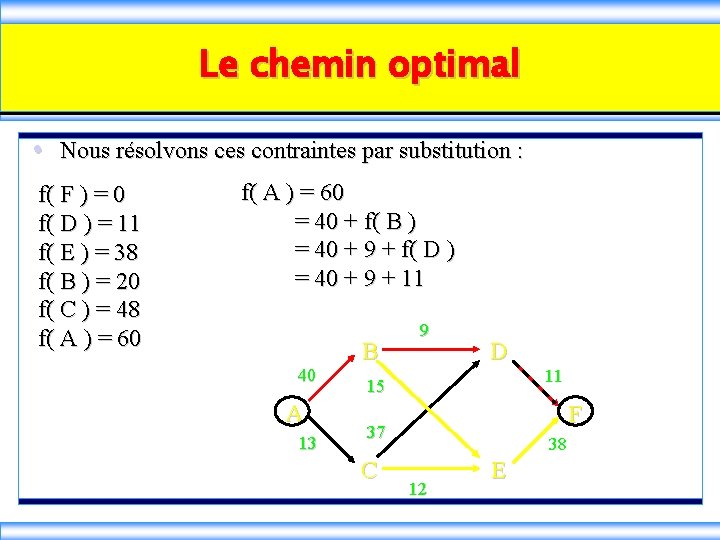
Le chemin optimal • Nous résolvons ces contraintes par substitution : f( F ) = 0 f( D ) = 11 f( E ) = 38 f( B ) = 20 f( C ) = 48 f( A ) = 60 = 40 + f( B ) = 40 + 9 + f( D ) = 40 + 9 + 11 40 A 13 B 9 D 11 15 F 37 C 38 12 E

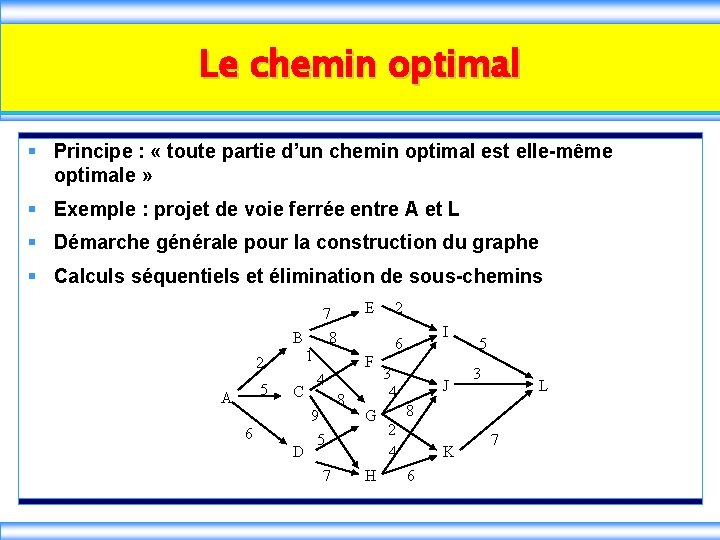
Le chemin optimal § Principe : « toute partie d’un chemin optimal est elle-même optimale » § Exemple : projet de voie ferrée entre A et L § Démarche générale pour la construction du graphe § Calculs séquentiels et élimination de sous-chemins 7 8 B 1 2 5 A C 6 D E 4 9 5 7 I 6 F 8 2 G H 3 4 J 5 3 L 8 2 4 K 6 7

L’optimisation des coûts par le moyen de la méthode hongroise

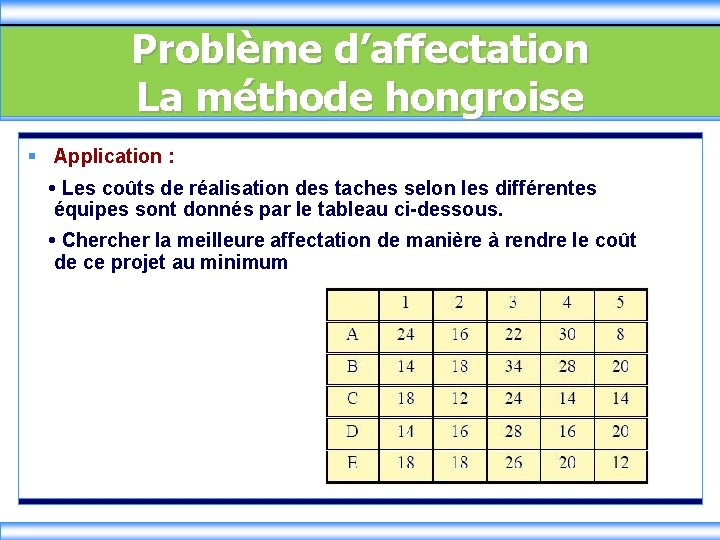
Problème d’affectation La méthode hongroise § Application : • Les coûts de réalisation des taches selon les différentes équipes sont donnés par le tableau ci-dessous. • Chercher la meilleure affectation de manière à rendre le coût de ce projet au minimum

Problème d’affectation La méthode hongroise § Etape 1: Obtention des zéros Créer une nouvelle matrice des coûts en choisissant le coût minimal dans chaque colonne et en le soustrayant de chaque coût dans la colonne ( Idem pour les lignes ).

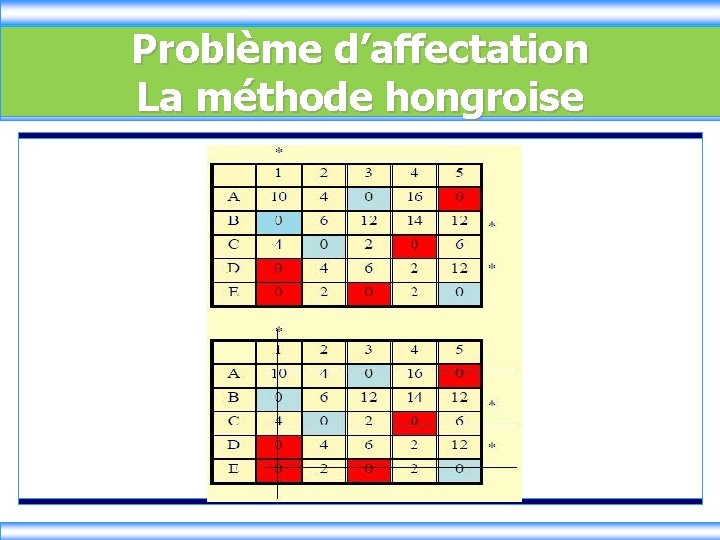
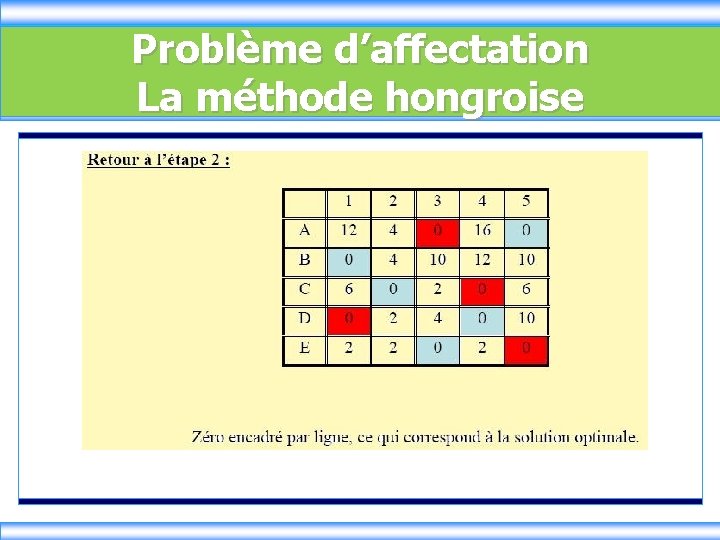
Problème d’affectation La méthode hongroise § Etape 2: Recherche d’une solution optimale - On cherche la ligne ou des lignes comptant le moins de zéro. - On encadre un des zéros de cette ligne, puis on barre les zéros qui se trouvent sur la même ligne et dans la même colonne que les zéros encadrés. - On répète le processus pour les lignes restantes. Un zéro encadré par ligne ⇒ Solution optimale

Problème d’affectation La méthode hongroise § La ligne 4 ne contient pas un zéro encadré donc on va appliquer l’étape 3 et 4 de l’algorithme.

Problème d’affectation La méthode hongroise § Etape 3: Recherche des rangées en nombre minimal contenant tous les zéros: a. On marque d’une croix toute ligne ne contenant aucun zéro encadré. b. On marque toute colonne qui a un zéro barré sur une ou plusieurs lignes marquées. c. On marque toute ligne qui a un zéro encadré sur une ou plusieurs colonnes marquées. d. On répète b) et c) jusqu’à ce qu’il n’y ait plus de colonne ou de ligne à marquer. On trace un trait sur toute colonne marquée. On trace un trait sur toute ligne non marquée.

Problème d’affectation La méthode hongroise

Problème d’affectation La méthode hongroise § Etape 4: Déplacement de certains zéros: -Tableau partiel : éléments traversés par aucun trait. - Le plus petit élément du tableau partiel est ajouté aux éléments rayés deux fois et retranché des éléments du tableau. - Retour à la phase 2.

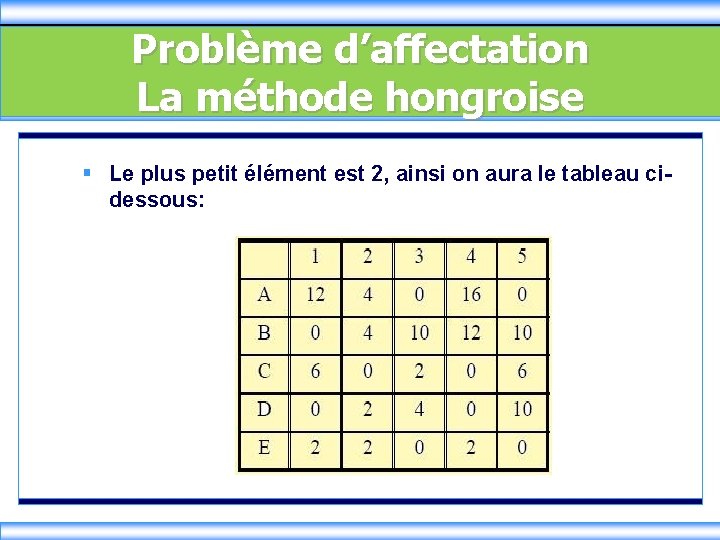
Problème d’affectation La méthode hongroise § Le plus petit élément est 2, ainsi on aura le tableau cidessous:

Problème d’affectation La méthode hongroise

Problème d’affectation La méthode hongroise