LA PARABOLA PREREQUISITI DISTANZA TRA DUE PUNTI Si

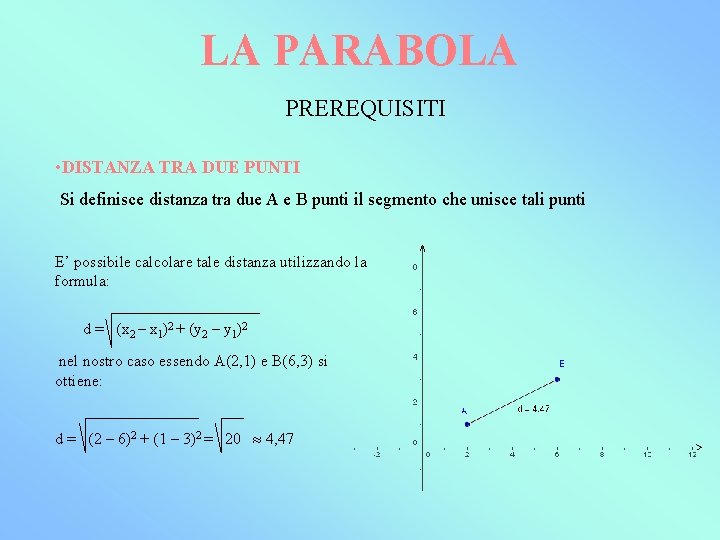
LA PARABOLA PREREQUISITI • DISTANZA TRA DUE PUNTI Si definisce distanza tra due A e B punti il segmento che unisce tali punti E’ possibile calcolare tale distanza utilizzando la formula: d = (x 2 – x 1)2 + (y 2 – y 1)2 nel nostro caso essendo A(2, 1) e B(6, 3) si ottiene: d = (2 – 6)2 + (1 – 3)2 = 20 4, 47

• RETTA Una retta generica nel piano cartesiano ha equazione y = mx + q (forma esplicita) ax + by + c = 0 (forma implicita) Ricordiamo che: m rappresenta il coefficiente angolare della retta ed esprime l’inclinazione della retta rispetto al semiasse positivo delle x q rappresenta l’ordinata all’origine ossia l’ordinata del punto d’intersezione della retta con l’asse y Nella retta in figura si ha m=2 e q=1 Vai al file Geogebra

• DISTANZA PUNTO RETTA La distanza tra una retta r ed un punto A del piano cartesiano è il tratto d di perpendicolare che va dal punto alla retta. Se il punto è A(xo, yo) e la retta ha equazione y = mx+q è possibile calcolare tale distanza utilizzando la formula: d= | yo – (mxo + q) | 1 + m 2 nel nostro caso essendo A(1, 7) e r: y = x-2 si ha: |7 - (1 -2)| 8 d= 5, 66 = 1 + 12 Vai al file Geogebra 2

• LUOGO GEOMETRICO Si definisce luogo geometrico l’insieme di tutti e soli i punti del piano che godono di una particolare proprietà. Ad esempio la circonferenza è il luogo geometrico dei punti del piano equidistanti da un punto fisso detto centro. Un altro luogo geometrico è l’asse di un segmento ossia la retta passante per il punto medio di un segmento e perpendicoalre ad esso. Si dimostra che tutti i suoi punti sono equidistanti dagli estremi del segmento.

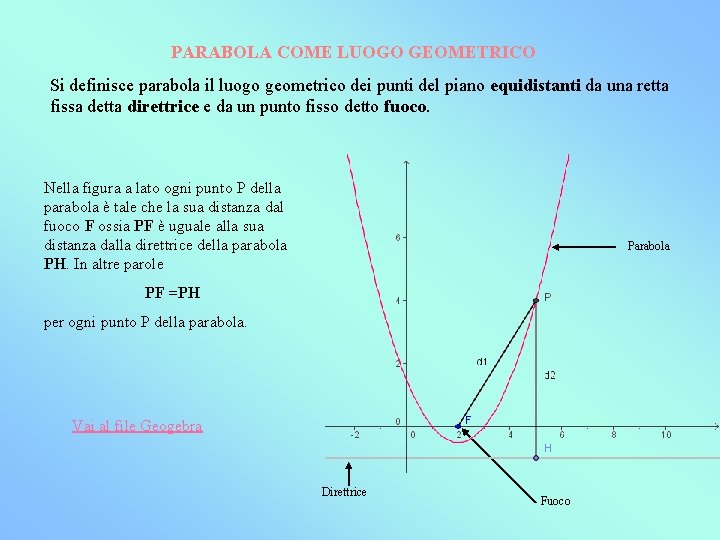
PARABOLA COME LUOGO GEOMETRICO Si definisce parabola il luogo geometrico dei punti del piano equidistanti da una retta fissa detta direttrice e da un punto fisso detto fuoco. Nella figura a lato ogni punto P della parabola è tale che la sua distanza dal fuoco F ossia PF è uguale alla sua distanza dalla direttrice della parabola PH. In altre parole Parabola PF =PH per ogni punto P della parabola. Vai al file Geogebra Direttrice Fuoco

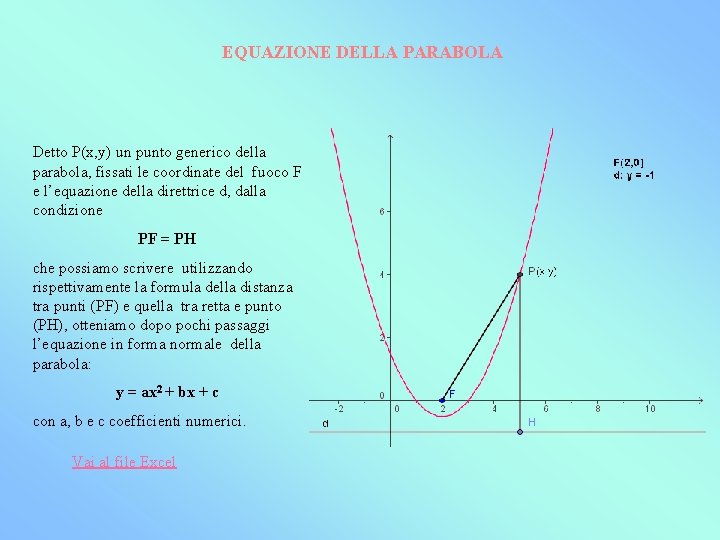
EQUAZIONE DELLA PARABOLA Detto P(x, y) un punto generico della parabola, fissati le coordinate del fuoco F e l’equazione della direttrice d, dalla condizione PF = PH che possiamo scrivere utilizzando rispettivamente la formula della distanza tra punti (PF) e quella tra retta e punto (PH), otteniamo dopo pochi passaggi l’equazione in forma normale della parabola: y = ax 2 + bx + c con a, b e c coefficienti numerici. Vai al file Excel

RAPPRESENTAZIONE GRAFICA DELLA PARABOLA Data l’equazione di una parabola y = ax 2 + bx + c per poterla rappresentare graficamente osserviamo che: 1) Se a > 0 la parabola volge la concavità verso l’alto 2) 3) Se a < 0 la parabola volge la concavità verso il basso 4) 2) V Il punto più in baso della parabola o più in alto V 3) vertice della parabola e le sue coordinate sono V[-b/2 a; -(b 2 -4 ac)/4 a] prende il nome di

RAPPRESENTAZIONE GRAFICA DELLA PARABOLA 3) L’asse della parabola è la retta verticale passante per il vertice ed è asse di simmetria della parabola stessa ossia ribaltando uno dei due rami della parabola rispetto a tale retta verrà esso a coincidere esattamente con l’altro ramo. La sua equazione sarà: x= -b/2 a 4) L’intersezione della parabola con l’asse y si ottiene risolvendo il sistema y = ax 2 + bx + c (Parabola) x=0 P (Asse y) ottenendo il punto P(0; c) 5) L’intersezione della parabola con l’asse x si ottiene invece risolvendo il sistema y = ax 2 + bx + c (Parabola) y=0 (Asse x) Da cui si perviene all’equazione di 2° grado ax 2 + bx + c = 0 Vai al file Excel

SIGNIFICATO GEOMETRICO DI UN’EQUAZIONE DI 2° GRADO Come abbiamo visto dunque, risolvere un’equazione di 2° grado ax 2 + bx + c = 0 è equivalente a trovare le intersezioni della parabola y = ax 2 + bx + c con l’asse x. Ricordando che con = b 2 -4 ac abbiamo indicato il discriminante dell’equazione generica di 2° grado e con x 1 e x 2 le soluzioni, possiamo classificare le parabole con lo schema seguente a>0 <0 a>0 =0 a>0 >0 x 1 x 2 a<0 <0 a<0 =0 x 1 x 2 x 1 a<0 >0 x 1 x 2