La mthode dEuler Objectif rsoudre une quation diffrentielle

La méthode d’Euler Objectif : résoudre une équation différentielle de façon numérique Applications en physique (en Terminale S): -Résoudre une équation différentielle du premier ordre (radioactivité, charge-décharge condensateur, chute avec frottement, etc. ) -… mais on peut résoudre aussi des équations différentielles d’ordre supérieur (voir TP Mercure) Intérêt : trouver une solution numérique quand la solution analytique est compliquée ou inaccessible

La méthode d’Euler : l’idée A partir de la connaissance de la valeur de la fonction pour une valeur de la variable - ex : pour xi, on connaît yi = f(xi) – on calcule la valeur suivante en utilisant la valeur de la dérivée . . il faut donc connaître un point (x 0, y 0) et la dérivée

La méthode d’Euler pas à pas Au départ, il y a : - une équation différentielle du premier ordre* y’(t) = d(y(t))/dt = fonction de y(t) qu’on ne sait pas nécessairement résoudre. . . - une condition initiale : c’est à dire une valeur que l’on connaît : Par exemple : y(0) = y 0 * Mais ça marche aussi pour un ordre plus élevé !

Un peu de math. . . Par définition, y’(t) = lim. Dt-->0 ([y(t+Dt) - y(t)]/Dt) En physique, pour un intervalle de temps Dt suffisamment petit (mais fini et défini) : y’(t) [y(t+Dt) - y(t)]/Dt d ’où y(t+Dt) y(t) + y’(t). Dt on note Dy(t) = y(t +Dt) - y(t) Dy(t) y’(t). Dt

Attention : quand le mathématicien écrit le physicien écrit = mais il ne faut pas perdre de vue que le résultat est approché ! Soit donc : Dy(t) = y(t +Dt) - y(t) Dy(t) = y’(t). Dt y(t +Dt) = y(t) + Dy(t) Tout cela à chaque instant t. . .

Rappel : on connaît une équation différentielle du premier degré (caractéristique du phénomène physique étudié) donc. . . y’(t) = fonction de y(t) Dy(t) = y’(t). Dt y(t +Dt) = y(t) + Dy(t) On connaît aussi a priori une valeur de y(t) : c’est la condition initiale : y(0) = y 0

Condition initiale y(0) y’(t) = fonction de y(t) Dy(t) = y’(t). Dt On connait y(0) => calcul de y’(0) Soit Dt ( « petit » ): le pas On a calculé y’(0), => calcul de Dy(0) y(t +Dt) = y(t) + Dy(t) On a calculé y(0) et Dy(0)=>calcul y(0+Dt) On a ainsi y(t 1) avec t 1 = 0 + Dt

On répète les opérations :

y(ti) Dy(ti) y’(ti) y(ti +Dt) A partir de xi, y’i = f’(xi) on calcule y(ti+1) avec ti+1 = ti +Dt Et ainsi de suite … c’est une méthode itérative

Le mieux est encore d’utiliser un exemple concret La décharge d’un condensateur chargé

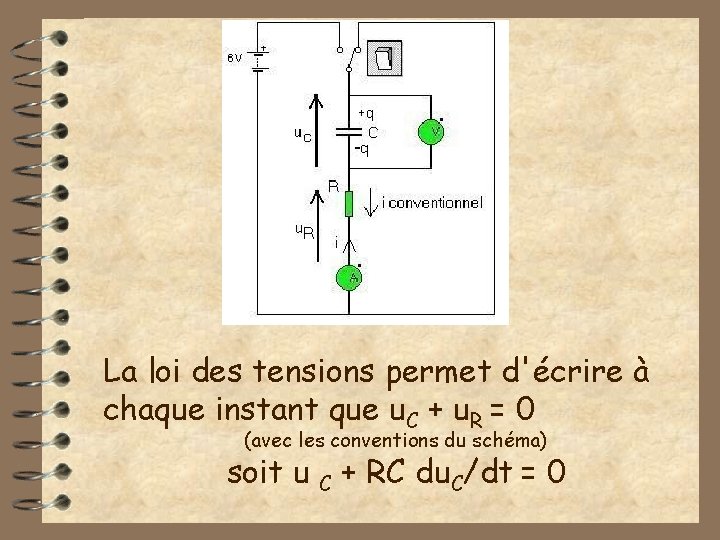
La loi des tensions permet d'écrire à chaque instant que u. C + u. R = 0 (avec les conventions du schéma) soit u C + RC du. C/dt = 0

Condition initiale u. C(0) u. C’(t) = - (1/RC). u. C(t) pas « petit » par rapport à quoi ? u. C’(0)= - (1/RC). u. C(0) Du. C(t) = u. C’(t). Dt Pas : Dt ( « petit » ) Du. C(0) = - (1/RC). u. C(0). Dt y(t +Dt) = y(t) + Dy(t) u. C(0+Dt) = u. C(0) - (1/RC). u. C(0). Dt t 1 = 0 + Dt u. C(t 1) est connu

Exigences du baccalauréat : Savoir appliquer la méthode d’Euler dans différents contextes - Dans un tableur - Savoir calculer (avec calculette) quelques étapes de la méthode Epreuve expérimentale (E. C. E) Epreuve écrite