La fonction quadratique Rvision k Sh k parabole

La fonction quadratique Révision

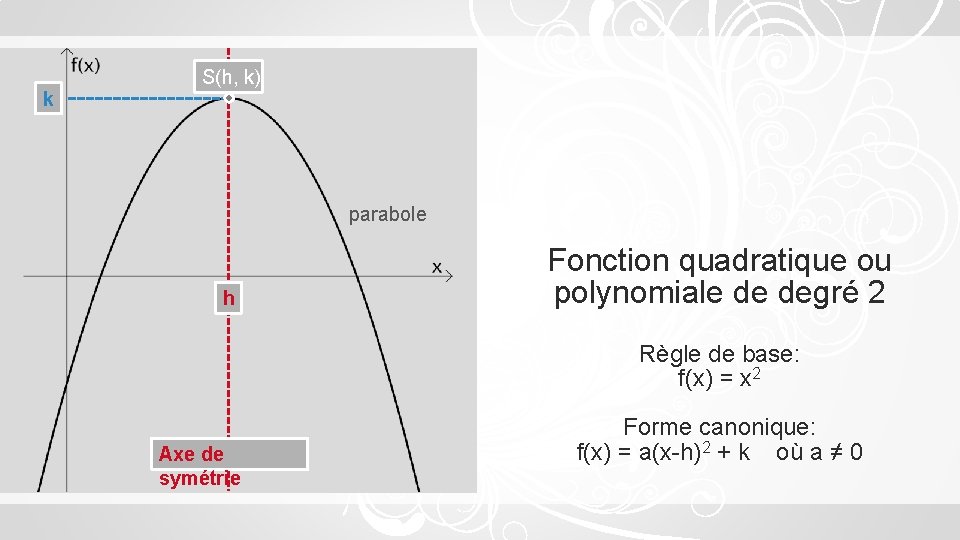
k S(h, k) parabole h Fonction quadratique ou polynomiale de degré 2 Règle de base: f(x) = x 2 Axe de symétrie Forme canonique: f(x) = a(x-h)2 + k où a ≠ 0

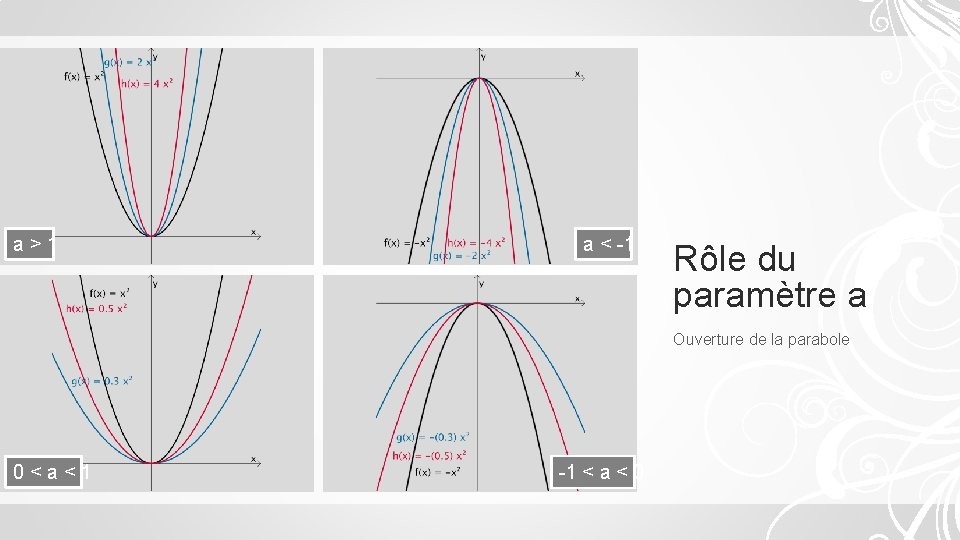
a>1 a < -1 Rôle du paramètre a Ouverture de la parabole 0<a<1 -1 < a < 0

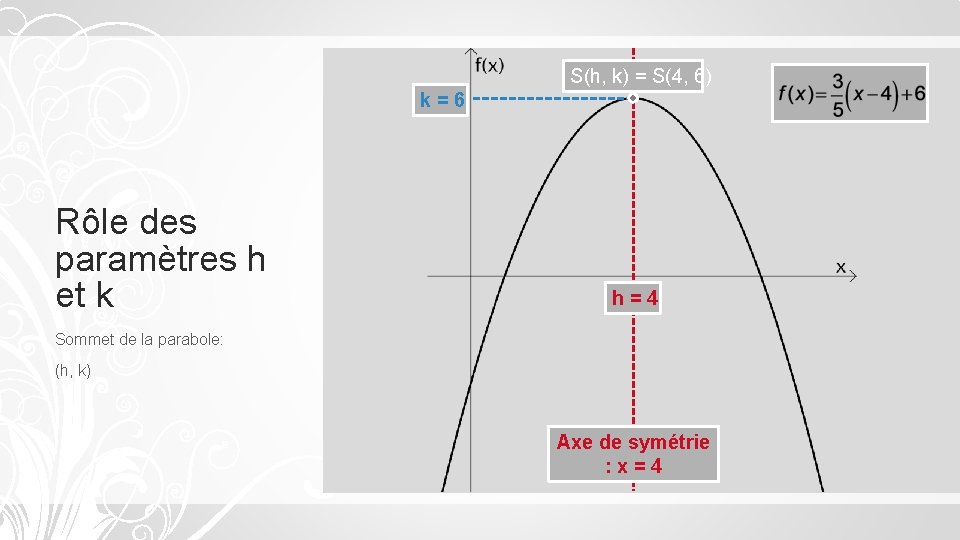
S(h, k) = S(4, 6) k=6 Rôle des paramètres h et k h=4 Sommet de la parabole: (h, k) Axe de symétrie : x=4

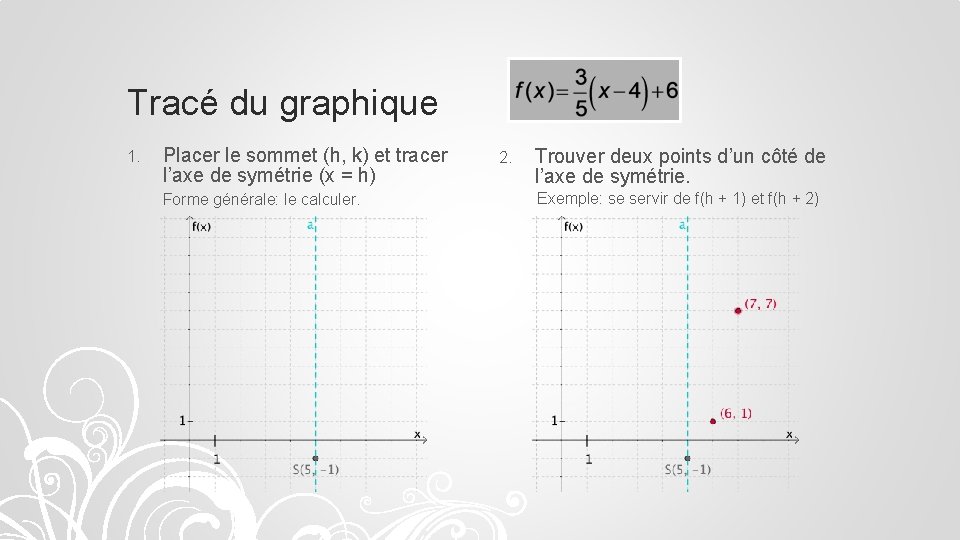
Tracé du graphique 1. Placer le sommet (h, k) et tracer l’axe de symétrie (x = h) Forme générale: le calculer. 2. Trouver deux points d’un côté de l’axe de symétrie. Exemple: se servir de f(h + 1) et f(h + 2)

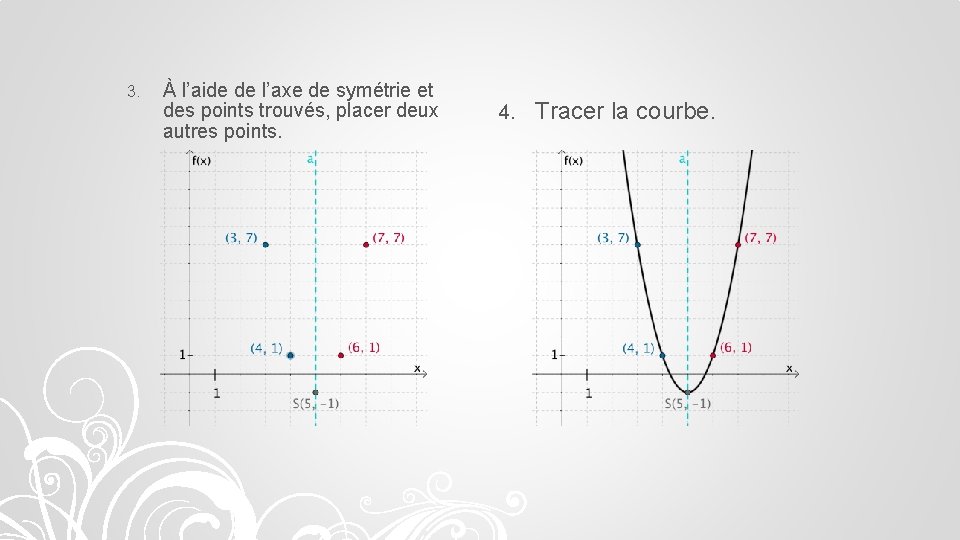
3. À l’aide de l’axe de symétrie et des points trouvés, placer deux autres points. 4. Tracer la courbe.

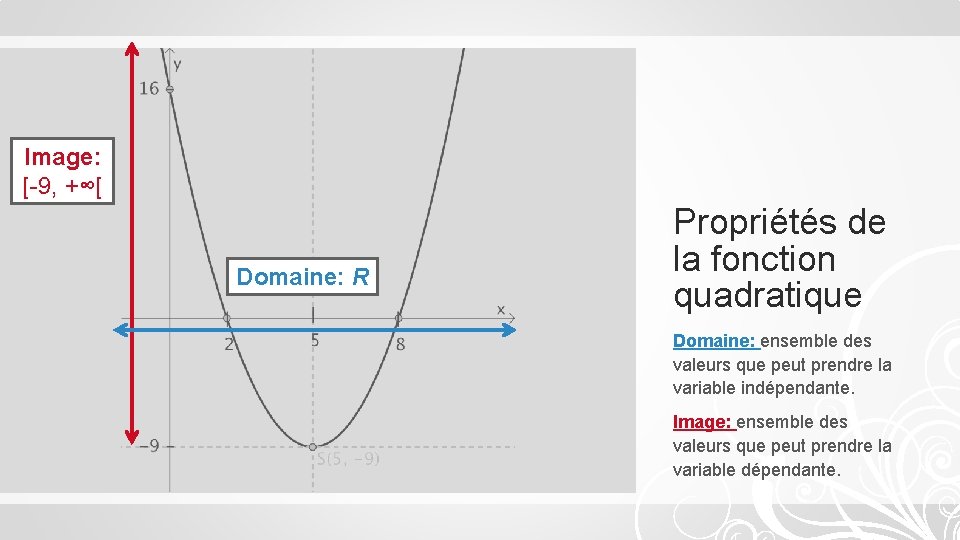
Image: [-9, +∞[ Domaine: R Propriétés de la fonction quadratique Domaine: ensemble des valeurs que peut prendre la variable indépendante. Image: ensemble des valeurs que peut prendre la variable dépendante.

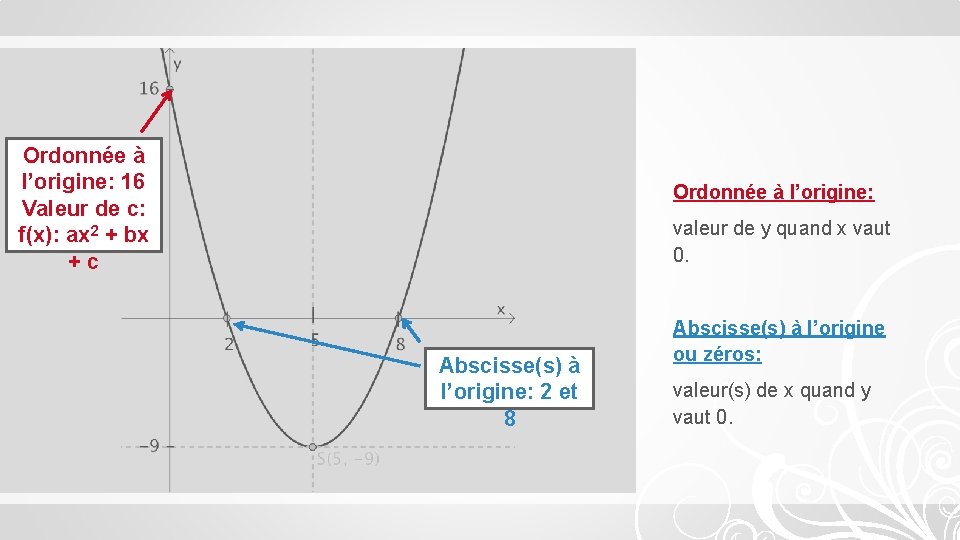
Ordonnée à l’origine: 16 Valeur de c: f(x): ax 2 + bx +c Ordonnée à l’origine: valeur de y quand x vaut 0. Abscisse(s) à l’origine: 2 et 8 Abscisse(s) à l’origine ou zéros: valeur(s) de x quand y vaut 0.

Décroissante : x ]-∞, 5] Croissante: x [5, +∞[ Variation Croissante: valeurs de x pour lesquelles la valeur de y augmente. Décroissante: valeurs de x pour lesquelles la valeur de y diminue.

Positive: x ]-∞, 2] [8, +∞[ Signe Négative: x [2, 8] Positive: valeurs de x pour lesquelles la valeur de y est positive. Négative: valeurs de x pour lesquelles la valeur de y est négative.

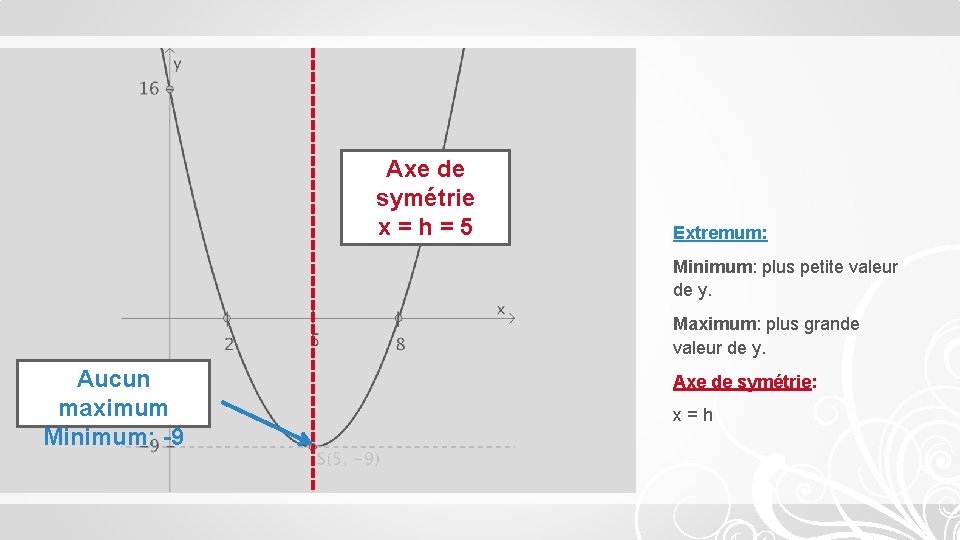
Axe de symétrie x=h=5 Extremum: Minimum: plus petite valeur de y. Maximum: plus grande valeur de y. Aucun maximum Minimum: -9 Axe de symétrie: x=h

• Forme canonique: Exemple: Résolution d’une équation Isoler x, puis effectuer la racine carrée de chacun des membres de l’équation.

• Forme générale: Exemple: Résolution d’une inéquation: 1. Remplacer le symbole d’inégalité par un symbole d’égalité. 2. Résoudre l’équation. 3. Esquisser la parabole et interpréter le graphique. Résolution d’une équation Transformer l’équation pour l’amener sous la forme 0 = ax 2 + bx + c et utiliser la formule :

Passage d’une forme à une autre * a est le même d’une forme à l’autre. Sommet Zéro(s) Ordonnée à l’origine Forme canonique: f(x) = a(x - h)2 + k (h, k) f(x) = 0 Isoler x. f(0) X 1 et x 2 f(0) f(x) = 0 Isoler x. f(0) = c Forme factorisée: f(x) = a(x – x 1)(x – x 2) k = f(h) Forme générale: f(x) = ax 2 + bx + c k = f(h)