La fonction Parabole Quadratique polynomiale de degr 2

La fonction Parabole Quadratique polynomiale de degré 2

Fonction quadratique ou parabole

Forme canonique

Forme factorisée

Forme générale

Remarque importante n. Le paramètre « a » est le même peu importe la forme de la fonction quadratique.

Paramètre « a »

Avantages de chacune des formes n Forme canonique : on connaît les coordonnées du sommet. n Forme générale : on connaît l’ordonnée à l’origine. n Forme factorisée : on connaît les coordonnées des zéros.

Générale à canonique

Canonique à générale

Générale à factorisée

Factorisée à générale

À partir du sommet et d’un point. n On doit utiliser la forme canonique.

À partir des zéros et d’un point. n On doit utiliser la forme factorisée.

À partir des zéros et d’un point. n On peut aussi utiliser la formule :

À partir d’une table de valeurs. On recherche les zéros ou le sommet dans notre table de valeurs. n Puisqu’une parabole possède un axe de symétrie vertical, on essaie de repérer les points qui possèdent la même ordonnée. Le sommet se trouve au centre de ces points. n

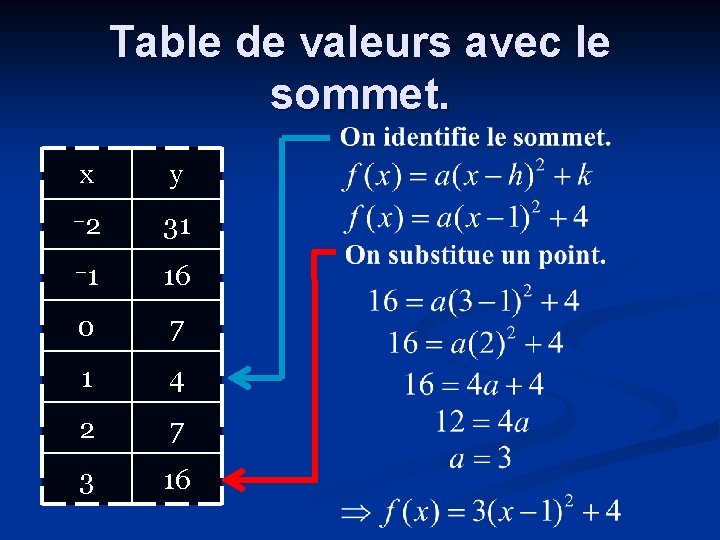
Table de valeurs avec le sommet. x y – 2 31 – 1 16 0 7 1 4 2 7 3 16

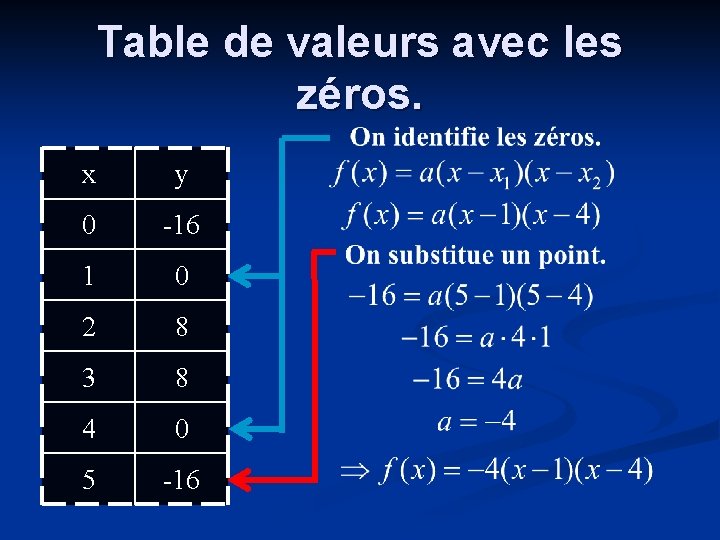
Table de valeurs avec les zéros. x y 0 -16 1 0 2 8 3 8 4 0 5 -16

Acroissements Les accroissements de la variable dépendante (y) sont constants pour des accroissements constants de la variable indépendante (x). n En d’autres termes, les acroissements de 2 e niveau de la variable dépendante sont constants. n

Reconnaître une quadratique dans une table de valeurs X Y -5 12, 5 0 0 5 12, 5 10 50 15 112, 5 20 200

Symétrie… n On peut parfois reconnaître une fonction quadratique dans une table de valeurs grâce à la symétrie de cette fonction. n X -6 -3 0 Y 180 45 0 3 45 6 180 On doit quand même vérifier les acroissements…

Autre formule… n À partir de la forme canonique, on peut trouver les zéros de la parabole à partir de la formule suivante :

Exemple

Trouver l’équation à partir des zéros et d’un point (méthode somme/produit) n Lorsque nous connaissons les zéros de la parabole, il est possible de trouver l’équation de la fonction avec :

Exemple n Trouver la règle de la fonction quadratique dont les zéros sont (-3, 0) et (5, 0) et qui passe par le point (2, -15).