La classification Plan n n n Dfinition et

La classification

Plan n n n Définition et Objectifs Analyse discriminante Régression logistique Arbres de décision Réseaux bayésiens Exemple

Définition et Objectifs Prévoir l’appartenance à une « classe » non observée à partir de variables observées n n Rappel sur la terminologie (Stat/Marketing) Applications typiques n Scoring de risque n n Connaissant les caractéristiques individuelles d’un emprunteur, quel est le risque qu’il ne rembourse pas son crédit ? Scoring marketing n A qui envoyer le mailing de lancement d’un nouveau produit ?

Caractérisation n n Un problème supervisé (par opposition à la segmentation ou à l’association) Deux utilisations : n n n Utilisation descriptive n n Descriptive : Déterminer les “règles” de séparation Décisionnelle : Attribuer un nouvelle individu à une classe. Problème de type géométrique Utilisation décisionnelle n Problème de type probabiliste. La nature fondamentale du problème est un calcul de probabilité conditionnelle : n n P(Incident|Caractéristiques) P(Réponse. Mailing|…)

Caractérisation (suite) n n Les variables observées peuvent être Qualitatives ou quantitatives La variable à prévoir est binaire (Oui/Non) ou discrète Le modèle est mis au point sur un ensemble de données où toutes les variables sont observées (y compris la classe) Exemple : Score de crédit n n n Données : Historique de dossiers de crédit Variables explicatives : CSP, Age, Revenus, Situation Familiale, etc. Variable à prévoir : Incident de remboursement

Techniques disponibles n n n Analyse factorielle discriminante Modèle logit/probit Arbres de décision Réseaux bayésiens Réseaux neuronaux

Analyse factorielle discriminante

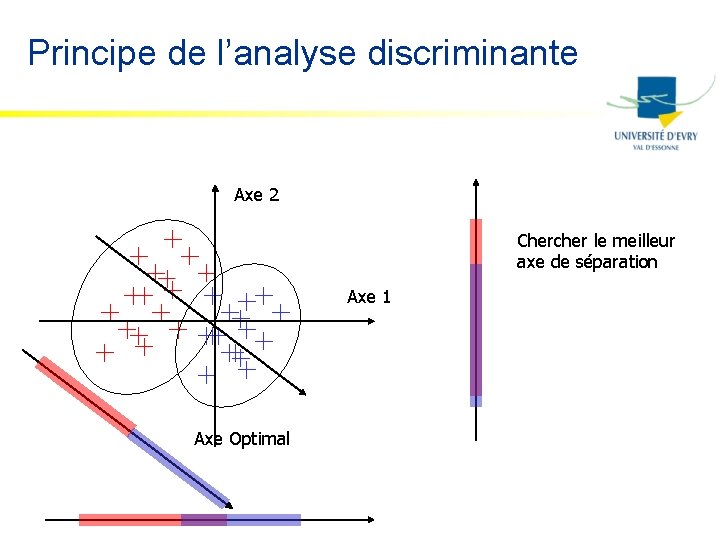
Analyse discriminante n n n Méthode géométrique (descriptive) Basée uniquement sur une notion de distance Maximisation du rapport Inertie Interclasse / Inertie totale

Principe de l’analyse discriminante Axe 2 Chercher le meilleur axe de séparation Axe 1 Axe Optimal

Régression logistique

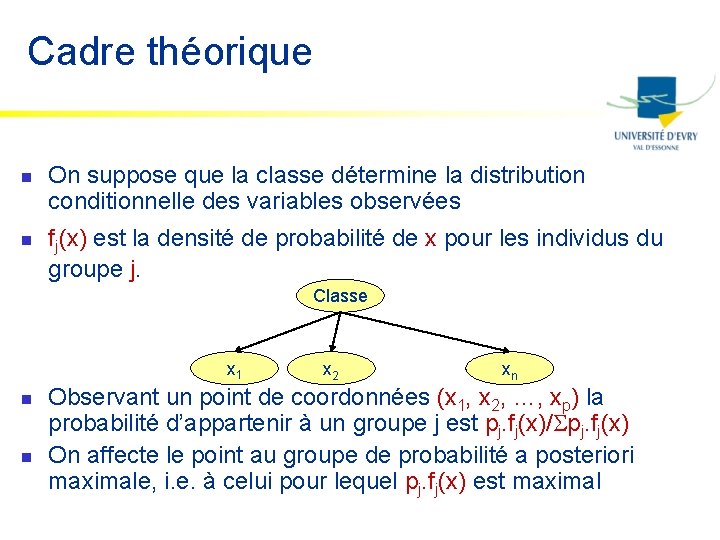
Cadre théorique n n On suppose que la classe détermine la distribution conditionnelle des variables observées fj(x) est la densité de probabilité de x pour les individus du groupe j. Classe x 1 n n x 2 xn Observant un point de coordonnées (x 1, x 2, …, xp) la probabilité d’appartenir à un groupe j est pj. fj(x)/ pj. fj(x) On affecte le point au groupe de probabilité a posteriori maximale, i. e. à celui pour lequel pj. fj(x) est maximal

Méthodes de résolution n Méthodes paramétriques n n n On choisit une famille paramétrée de lois de probabilité pour fj(x) Les observations permettent d’estimer les paramètres Méthodes non paramétriques n Variantes de la méthode du noyau

Cas simple n Hypothèses n n n On considère deux classes, et f 1(x) et f 2(x) suivent une loi normale Les matrices de variance/covariance sont identiques pour les deux classes Résultat n n On peut calculer un score s(x) fonction linéaire des variables x. La probabilité d’appartenance au groupe 1 est alors p=1/(1+exp(-s(x)))

La régression logistique n n On part de la forme obtenue précédemment p=1/(1+exp(-s(x))) Qui se transforme en : s(x)=ln(p/1 -p) s(x) est une combinaison linéaire des xi s(x)= 0+ 1. x 1+ 1. x 2+…+ 1. xn Ses coefficients i sont estimés par le MV L=∏i C 1 f 1(xi) ∏i C 2 f 2(xi)

Arbres de décision

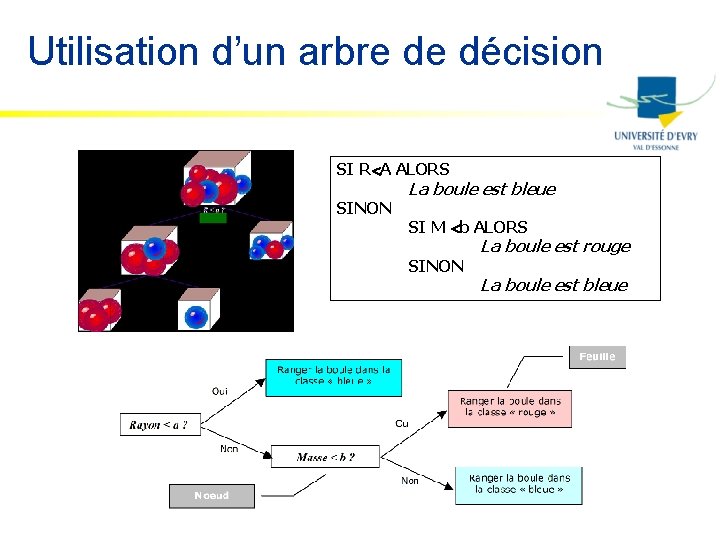
Arbres de décision n Une méthode de régression n n Basée sur la théorie de l’information Fonctionnant pour des variables continues ou discrètes Recherche itérative de variables discriminantes Produisant des modèles faciles à interpréter (sous forme de règles SI … ALORS … SINON)

Principe n n Un arbre de décision est construit récursivement En recherchant à chaque fois le critère qui fait gagner le plus d’ « ordre »

Utilisation d’un arbre de décision SI R A ALORS SINON La boule est bleue SI M b ALORS SINON La boule est rouge La boule est bleue

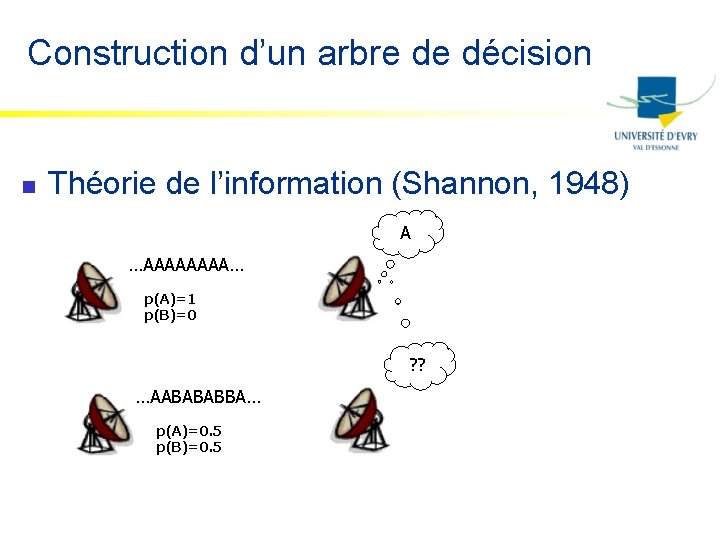
Construction d’un arbre de décision n Théorie de l’information (Shannon, 1948) A …AAAA… p(A)=1 p(B)=0 ? ? …AABABABBA… p(A)=0. 5 p(B)=0. 5

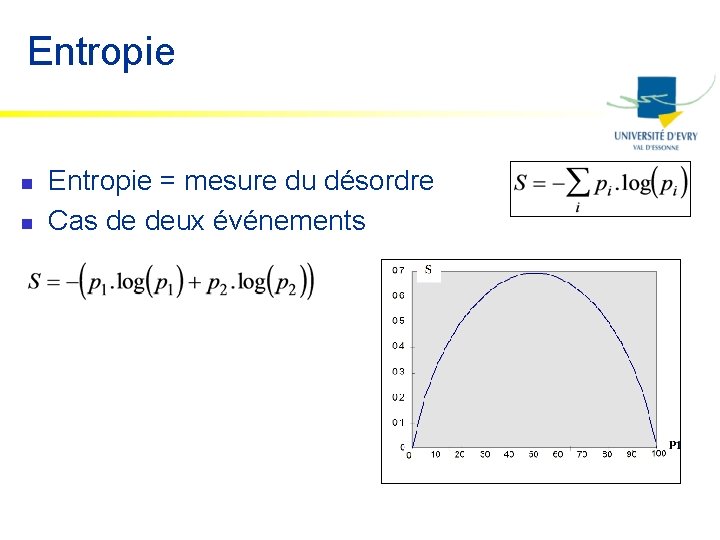
Entropie n n Entropie = mesure du désordre Cas de deux événements

Algorithme C 4. 5 Si E ne contient que des éléments de la même classe Terminer Sinon Trouver le test T qui fasse gagner le plus d’entropie T sépare E en E 1 et E 2 : Appliquer C 4. 5 à E 1 et E 2

Exemple d’arbre obtenu Si Ancienneté Bancaire = 0 Risque Elevé Sinon (Ancienneté Bancaire > 0) Si Revenus <=4 Si Allocations <=2 Si Date. Embauche. Conjoint = 0 Si Date. Embauche <= 3 Risque Elevé Sinon (Date. Embauche > 3) Risque Faible Sinon (Date. Embauche. Conjoint > 0) Risque Faible Si Allocations >2 Risque Elevé Sinon (Revenus > 4) Risque Faible

Réseaux bayésiens

Les réseaux bayésiens q Introduction q L’inférence ou le calcul de P(X|e) q L’apprentissage ou le calcul de P q Applications des réseaux bayésiens q Conclusion

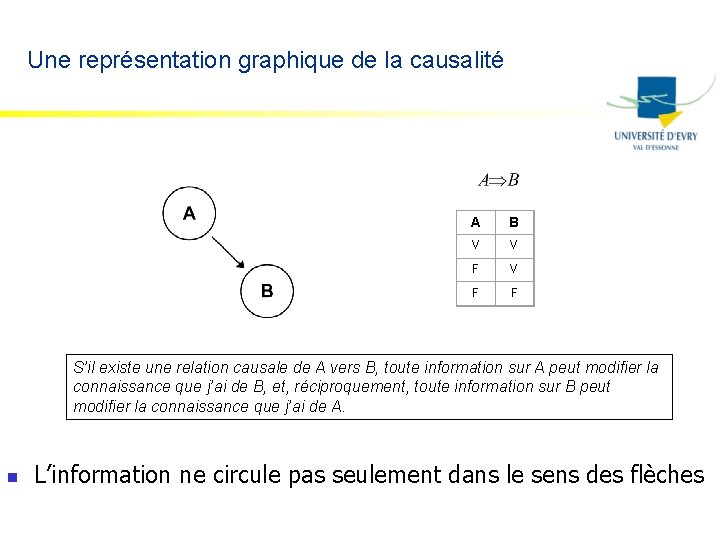
Une représentation graphique de la causalité A B V V F F S’il existe une relation causale de A vers B, toute information sur A peut modifier la connaissance que j’ai de B, et, réciproquement, toute information sur B peut modifier la connaissance que j’ai de A. n L’information ne circule pas seulement dans le sens des flèches

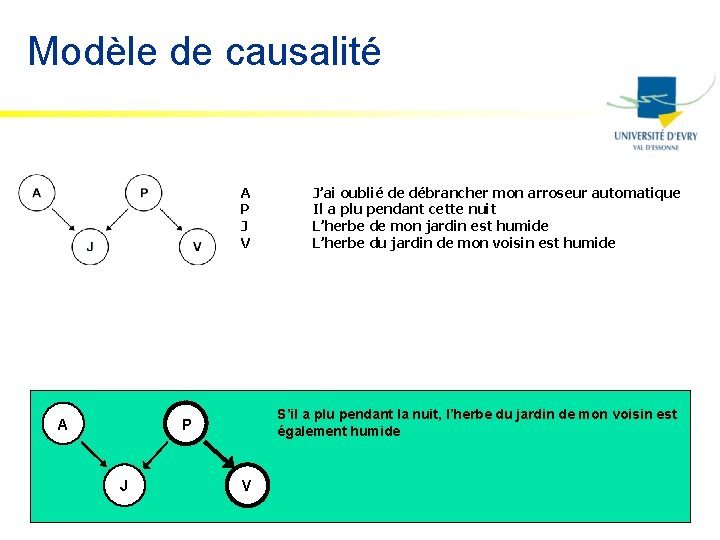
Sherlock Holmes & Thomas Bayes Ce matin-là, alors que le temps est clair et sec, M. Holmes sort de sa maison. Il s’aperçoit que la pelouse de son jardin est humide. Il se demande alors s’il a plu pendant la nuit, ou s’il a simplement oublié de débrancher son arroseur automatique. Il jette alors un coup d’œil à la pelouse de son voisin, M. Watson, et s’aperçoit qu’elle est également humide. Il en déduit alors qu’il a probablement plu, et il décide de partir au travail sans vérifier son arroseur automatique

Modèle de causalité A P J V A a plu pendant la nuit, l’herbe du jardin de mon voisin S’il Si a plu j’ai pendant oublié deladébrancher nuit, l’herbe mon de mon arroseur jardinautomatique, est humide. est également humide l’herbe de mon jardin est humide P J J’ai oublié de débrancher mon arroseur automatique Il a plu pendant cette nuit L’herbe de mon jardin est humide L’herbe du jardin de mon voisin est humide V

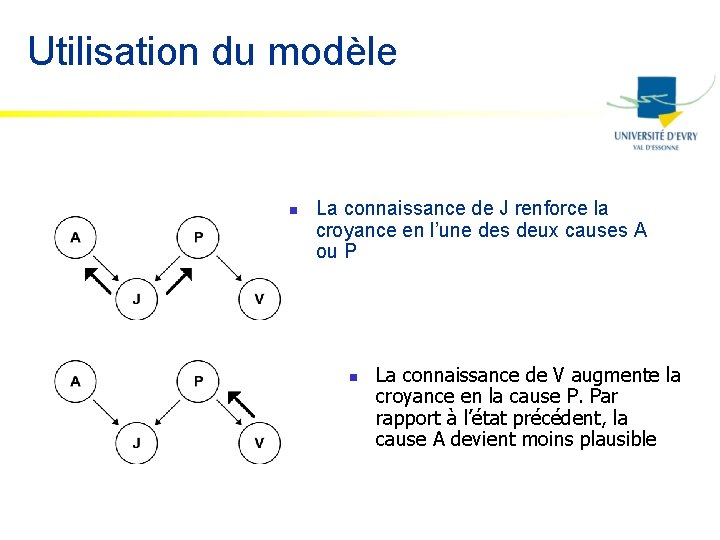
Utilisation du modèle n La connaissance de J renforce la croyance en l’une des deux causes A ou P n La connaissance de V augmente la croyance en la cause P. Par rapport à l’état précédent, la cause A devient moins plausible

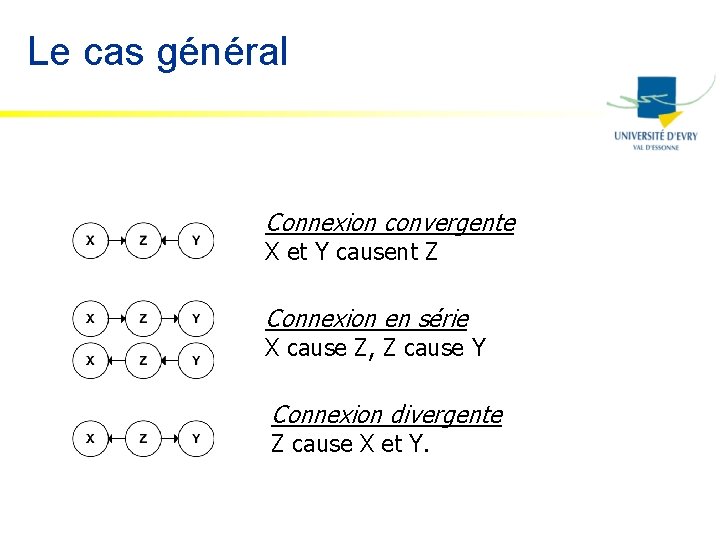
Le cas général Connexion convergente X et Y causent Z Connexion en série X cause Z, Z cause Y Connexion divergente Z cause X et Y.

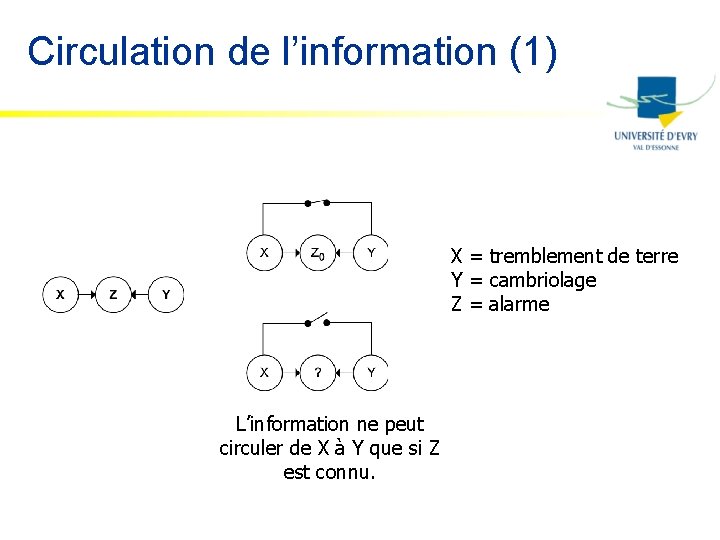
Circulation de l’information (1) X = tremblement de terre Y = cambriolage Z = alarme L’information ne peut circuler de X à Y que si Z est connu.

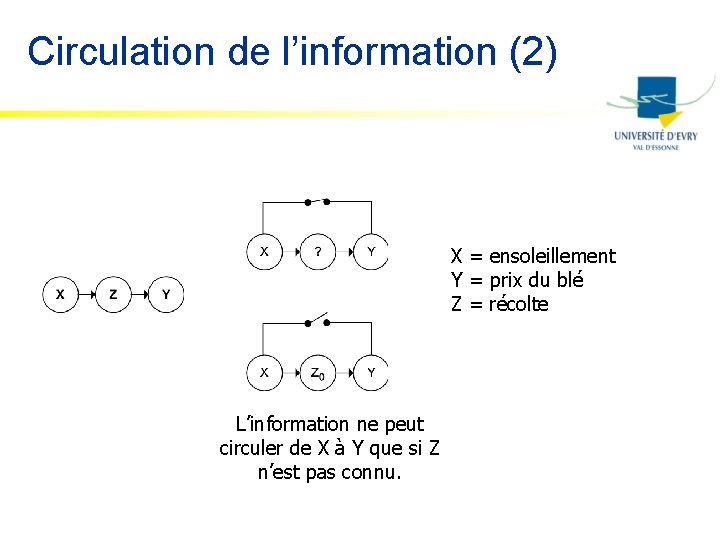
Circulation de l’information (2) X = ensoleillement Y = prix du blé Z = récolte L’information ne peut circuler de X à Y que si Z n’est pas connu.

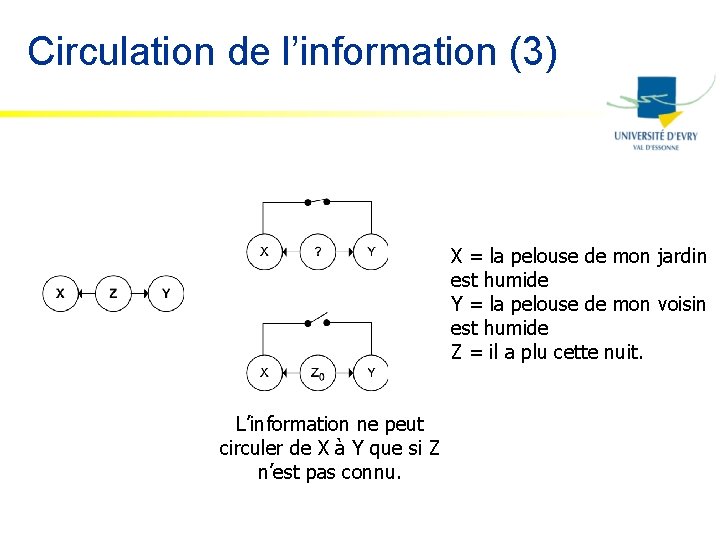
Circulation de l’information (3) X = la pelouse de mon jardin est humide Y = la pelouse de mon voisin est humide Z = il a plu cette nuit. L’information ne peut circuler de X à Y que si Z n’est pas connu.

d-séparation (blocage) On dira que X et Y sont d-séparés par Z si pour tous les chemins entre X et Y, l’une au moins deux conditions suivantes est vérifiée : · Le chemin converge en un nœud W, tel que W Z, et W n’est pas une cause directe de Z. · Le chemin passe par Z, et est soit divergent, soit en série au nœud Z. On notera X|Z|Y

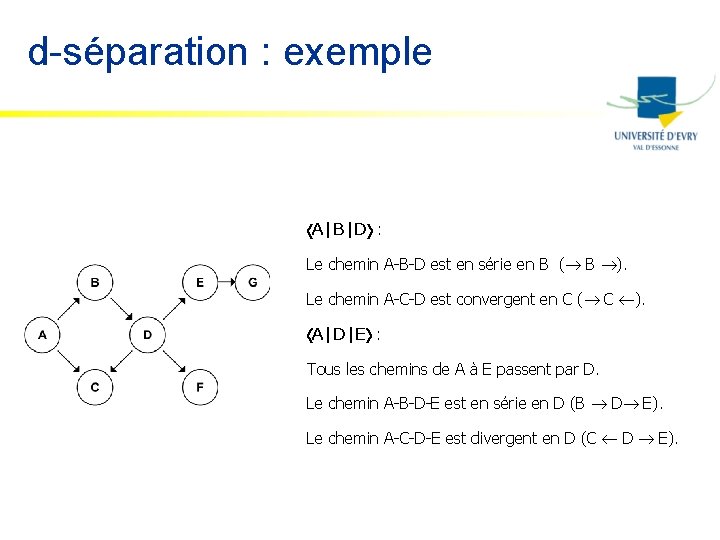
d-séparation : exemple A|B|D : Le chemin A-B-D est en série en B ( B ). Le chemin A-C-D est convergent en C ( C ). A|D|E : Tous les chemins de A à E passent par D. Le chemin A-B-D-E est en série en D (B D E). Le chemin A-C-D-E est divergent en D (C D E).

Une représentation probabiliste associée • • Un nœud = une variable aléatoire Si A n’a aucune cause directe, nous devrons définir p(A), c’est-à-dire les deux nombres p(A=Vrai) et p(A=Faux). Si B a une seule cause directe A, nous devrons définir p(B|A), c’est-à -dire les quatre nombres p(B=V|A=V), , etc. Si C a deux causes directes A et B nous devrons définir p(C|A, B), c’est-à-dire les huit nombres p(C=V|A=V, B=V) , etc.

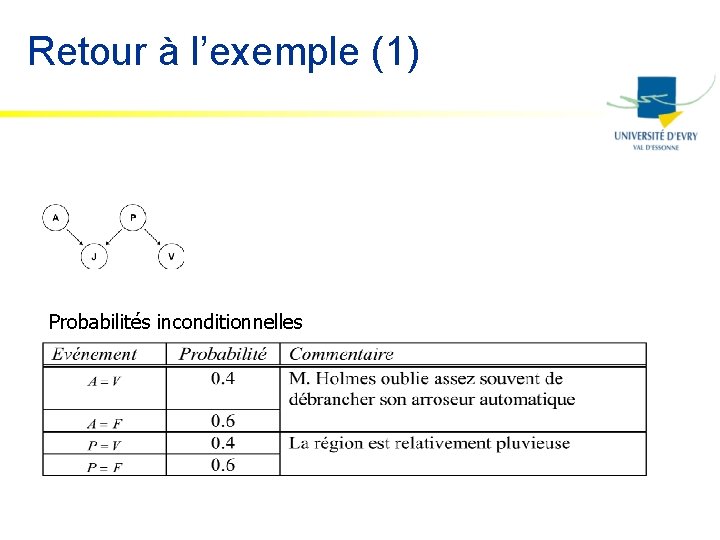
Retour à l’exemple (1) Probabilités inconditionnelles

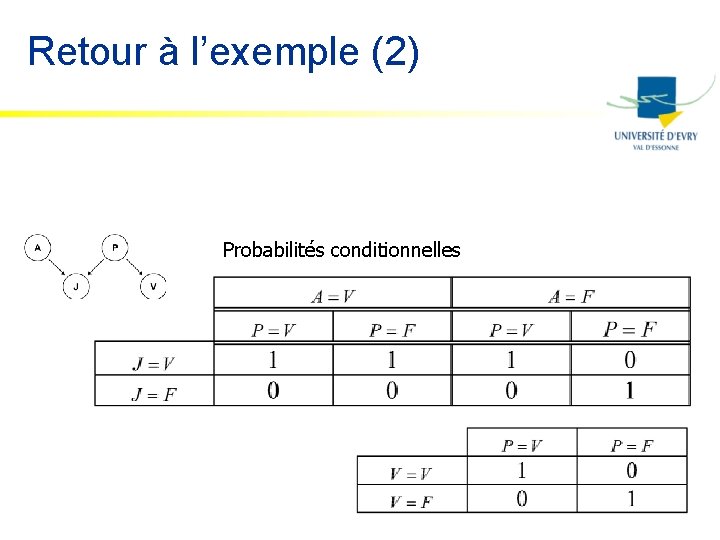
Retour à l’exemple (2) Probabilités conditionnelles

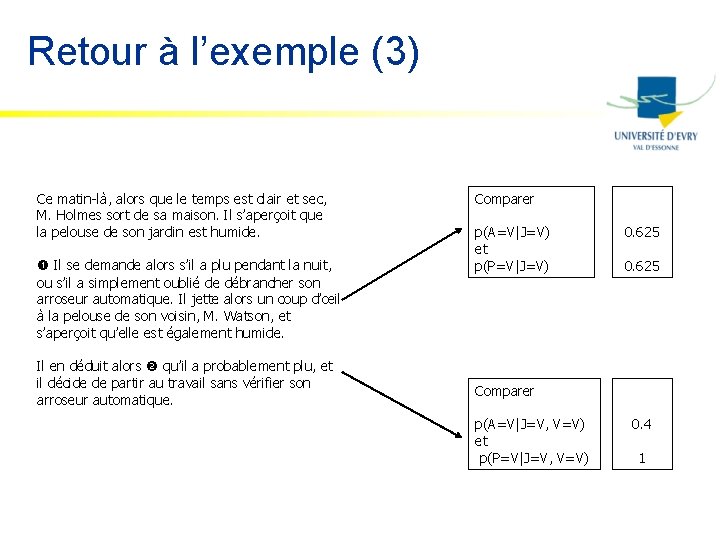
Retour à l’exemple (3) Ce matin-là, alors que le temps est clair et sec, M. Holmes sort de sa maison. Il s’aperçoit que la pelouse de son jardin est humide. Il se demande alors s’il a plu pendant la nuit, ou s’il a simplement oublié de débrancher son arroseur automatique. Il jette alors un coup d’œil à la pelouse de son voisin, M. Watson, et s’aperçoit qu’elle est également humide. Il en déduit alors qu’il a probablement plu, et il décide de partir au travail sans vérifier son arroseur automatique. Comparer p(A=V|J=V) et p(P=V|J=V) 0. 625 Comparer p(A=V|J=V, V=V) et p(P=V|J=V, V=V) 0. 4 1

Retour à l’exemple (4) n n A et P sont d-séparés Si J est connu, l’information peut circuler de A à P (A J P est une connexion convergente) n n n A et P sont indépendants P(A=F et P=F|J=V) = 0 P(A=F|J=V) = 0. 375 P(P=F|J=V) = 0. 375 A et P ne sont pas indépendants conditionnellement à J

Résumé n n La transposition d’un graphe causal en espace probabilisé conduit à des résultats conformes au raisonnement intuitif que l’on peut mener directement sur ce graphe Ces résultats sont quantitatifs Les calculs mis en œuvre, même sur des cas très simples, sont lourds Les propriétés graphiques (d-séparation) peuvent être mises en correspondance avec les propriétés d’indépendance de l’espace probabilisé associé.

Réseaux bayésiens : définition n Un réseau bayésien est défini par n n n un graphe acyclique orienté G = (V, E) , où V est l’ensemble des nœuds de G, et E l’ensemble des arcs de G un espace probabilisé fini (W, Z, P) un ensemble de variables aléatoires correspondant aux nœuds du graphe, telles que

Théorème fondamental n n n Soit B=(G, P) un réseau bayésien Si X, Y, Z sont des ensembles de nœuds tels que X et Y sont d-séparés dans G par Z, alors X et Y sont indépendants conditionnellement à Z

Inférence dans les réseaux bayésiens n n n Inférence = Révision des probabilités Calculer P(X|e) La complexité dépend de la complexité du réseau

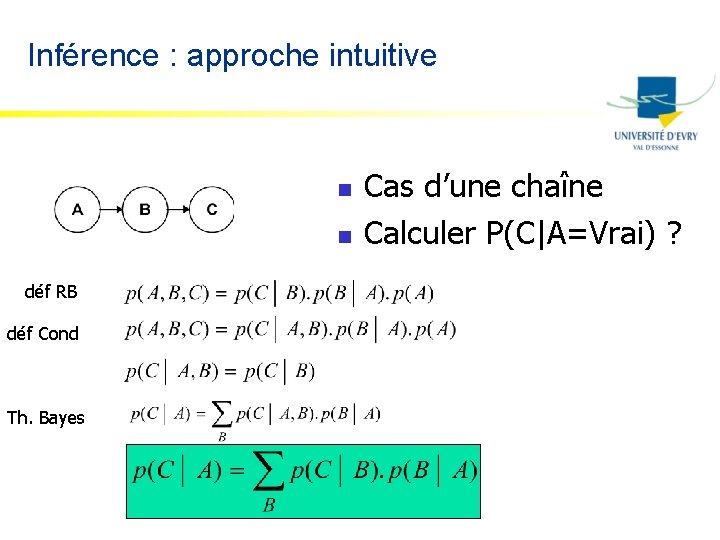
Inférence : approche intuitive n n déf RB déf Cond Th. Bayes Cas d’une chaîne Calculer P(C|A=Vrai) ?

Inférence : approche intuitive (suite) n Calculer P(E|A=Faux) ?

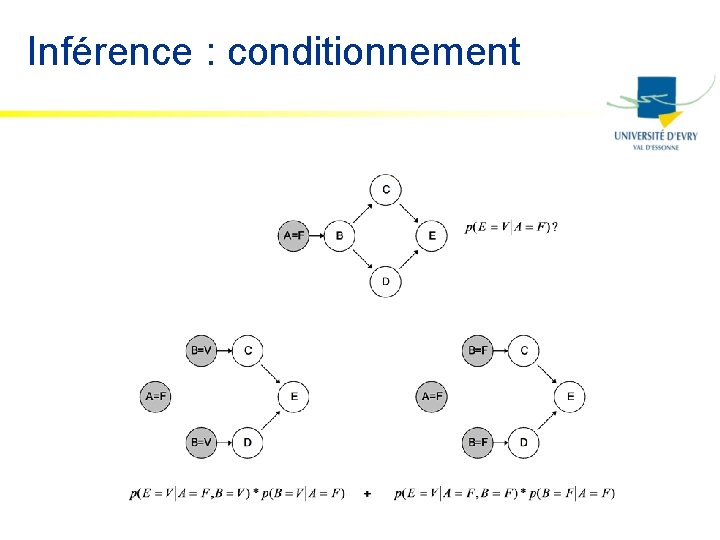
Inférence : conditionnement

Inférence : aspects théoriques n n Problème NP-complet dans le cas général Méthodes simples (réseaux sans boucles) Méthodes « graphiques » (réseaux avec boucles) Méthodes approchées (réseaux de grande taille)

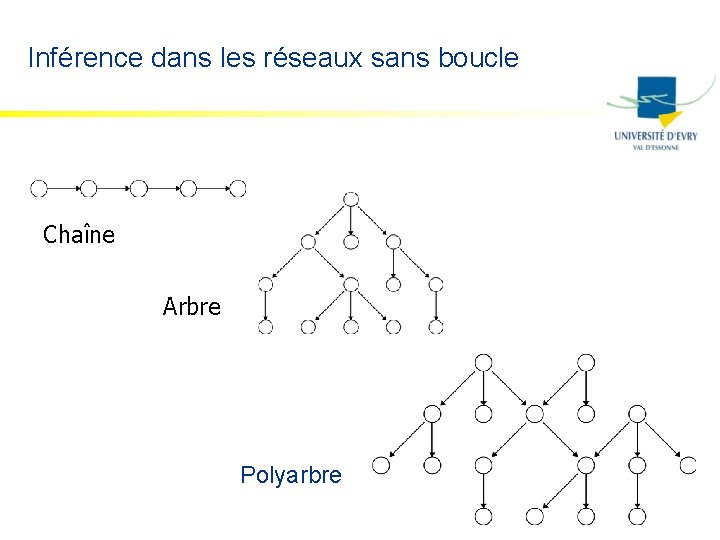
Inférence dans les réseaux sans boucle Chaîne Arbre Polyarbre

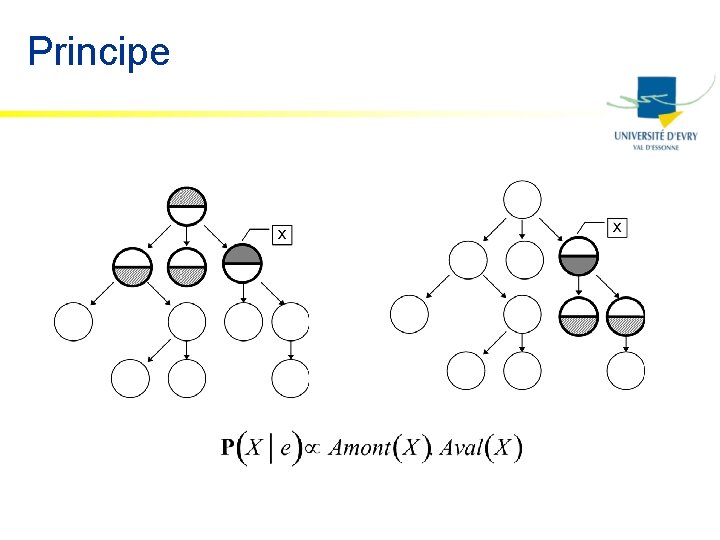
Principe

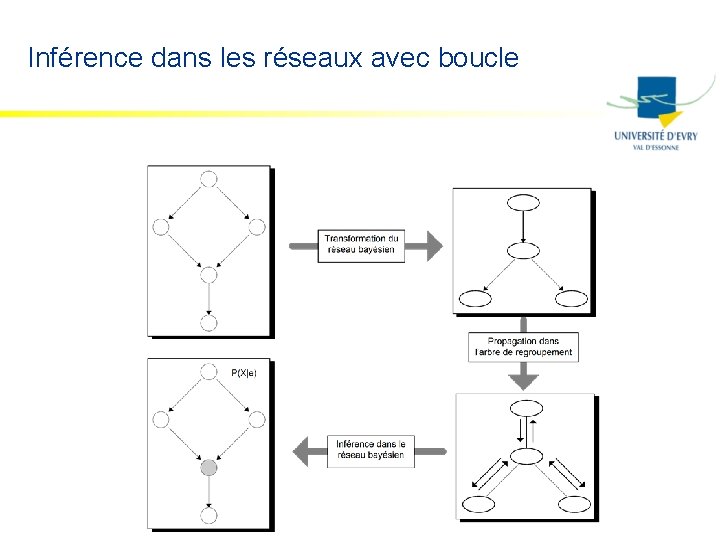
Inférence dans les réseaux avec boucle

A quoi sert un réseau bayésien ? n n Inférence = raisonnement à partir de données partielles Exemple d’application = diagnostic n n Médical Autre : évaluation de risque, scoring, etc.

Questions 1. D’où viennent les probabilités ? 2. D’où vient le graphe

Réponses 1. Apprentissage de paramètres n n La structure étant supposée connue, Utiliser une base de cas pour déterminer les tables de probabilités 2. Apprentissage de structure n Utiliser une base de cas pour déterminer les arcs du réseau

Approches n Trois possibilités n Demander aux experts du domaine: n n Approche statistique n n Surtout valable pour le graphe Calcul du maximum de vraisemblance Approche bayésienne n Distribution des paramètres ou de la structure postérieurement à l’observation des données

Exemple Comment estimer la probabilité q ? Fréquence Bayes

Apprentissage de paramètres n Ø La structure est donnée Le jeu de paramètres à estimer s’en déduit

Apprentissage statistique de paramètres n Approche Maximum de vraisemblance n Résultat : fréquences n

Apprentissage bayésien de paramètres n Formule générale A Posteriori = Vraisemblance. A Priori n Résultat n n dépend de la probabilité a priori cas de Dirichlet

Apprentissage statistique de structure n n n Contraindre la structure Cas général : ? Cas de l’arbre n n Théorème de Chow et Liu Arbre couvrant de poids maximal

Apprentissage bayésien de structure n Même principe général n Problème n n n Distribution des structures Calcul de P(M|D) Recherche (4. 1018 structures possibles pour dix variables)

Algorithme K 2

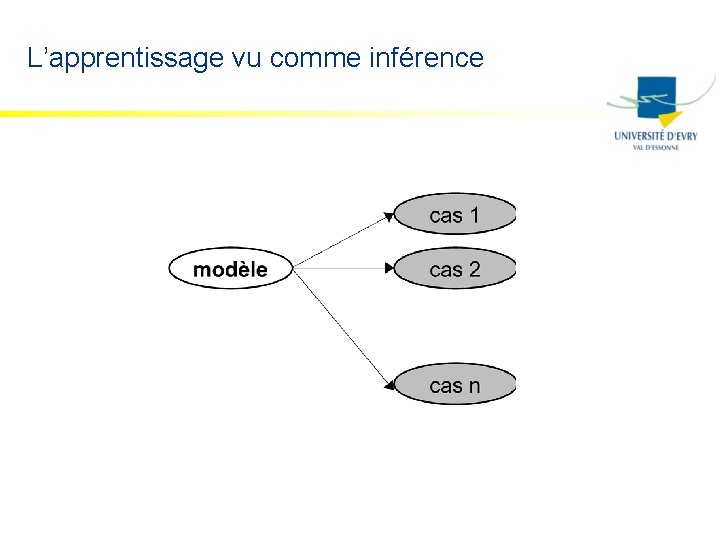
L’apprentissage vu comme inférence

Conclusions n Avantages n n n Formalisme unifié Apprentissage et apprentissage incrémental Données incomplètes Requêtes d’inférence multiples Limites n n n Complexité : inférence et apprentissage sont NP-complets ! Lisibilité Probabilités ?

Exemple Questionnaire adaptatif (Crédit en ligne) n Vendre sur Internet n n Vente de crédit n n n Risque de déconnexion Accélérer le processus de vente Risque d’impayé Obtenir des informations sur le client Compromis à trouver Variable-clé = longueur du questionnaire

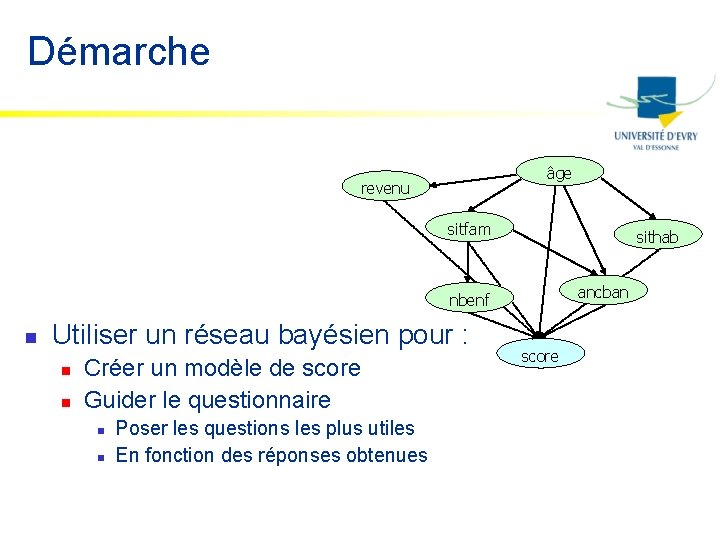
Démarche âge revenu sitfam sithab ancban nbenf n Utiliser un réseau bayésien pour : n n Créer un modèle de score Guider le questionnaire n n Poser les questions les plus utiles En fonction des réponses obtenues score

Questionnaire adaptatif n Principe n n n Un score d'acceptation (proba MP) définitif est fixé (S 1), par exemple 0. 06 Un score de rejet définitif est fixé (S 2), par exemple 0. 20 Le questionnaire adaptatif fonctionne comme suit : Tant. Que la proba MP est comprise entre S 1 et S 2, Faire Parmi les questions non encore posées, déterminer celle apportant le plus d'information Poser la question Calculer la nouvelle proba MP Fin Tant. Que

Résultats n n Nombre moyen de questions posées : 9 Questionnaires complets = 35% Nombre moyen de questions (incomplets) = 7 Erreurs = 4% n n Erreur BP = 4% Erreur MP = 4%