l l 2 Sampling Distribution Central Limit Theorem

綱要 l l 2 樣品統計量之分布(Sampling Distribution) 中央極限定理(Central Limit Theorem) 點估計(Point Estimation) 區間估計(Interval Estimation) 2020/11/22 Jen-pei Liu, Ph. D

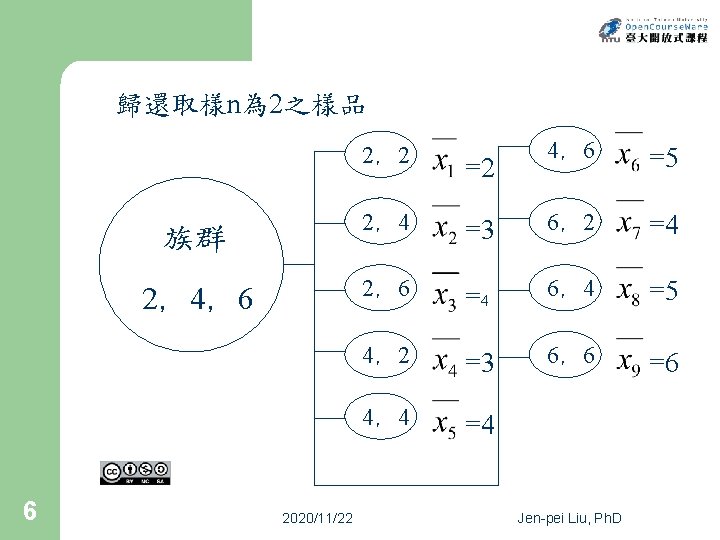
歸還取樣n為 2之樣品 族群 2，4，6 6 2020/11/22 4，6 =5 =3 6，2 =4 2，6 =4 6，4 =5 4，2 =3 6，6 =6 4，4 =4 2，2 =2 2，4 Jen-pei Liu, Ph. D

樣品 平均 7 1 2 3 4 5 6 7 8 9 2 2 2 4 4 4 6 6 6 2 4 6 2 3 4 5 4 5 6 2020/11/22 Jen-pei Liu, Ph. D

族群分佈 2 9 4 樣品平均值分佈 6 2 2020/11/22 3 4 5 6 Jen-pei Liu, Ph. D

族群變方 觀測值 11 機率 2 1/3 4 4/3 4 1/3 0 0/3 6 1/3 4 4/3 8/3= 2020/11/22 Jen-pei Liu, Ph. D

X = 70 n = 650 P = 0. 1 = np = (650)(0. 1) = 65 = npq = (650)(0. 1)(0. 9) = 58. 5 標準化值 � P(X > 70) = P(Z > 0. 65) = 1－P(Z < 0. 65) = 1－0. 7422 = 0. 2578 =25. 78% 16 2020/11/22 Jen-pei Liu, Ph. D

令X為二項分佈隨機變數 求 18 n=15 P=0. 4 （表 2值 0. 2121） 2020/11/22 Jen-pei Liu, Ph. D

20 2020/11/22 Jen-pei Liu, Ph. D

點估計值(Point Estimates) 族群 樣品 取樣 未知 21 推論(估計) 2020/11/22 Jen-pei Liu, Ph. D

下限： 29 上限： 2020/11/22 Jen-pei Liu, Ph. D

� 20 -30歲成人血液中尿酸濃度 31 2020/11/22 Jen-pei Liu, Ph. D

習題： l P. 130: 8 l P. 142： 2, 3, 5 36 2020/11/22 Jen-pei Liu, Ph. D