L I To solve scaling problems using measures

L. I. To solve scaling problems using measures Which words in the question are important? What would the question look like as a bar model?

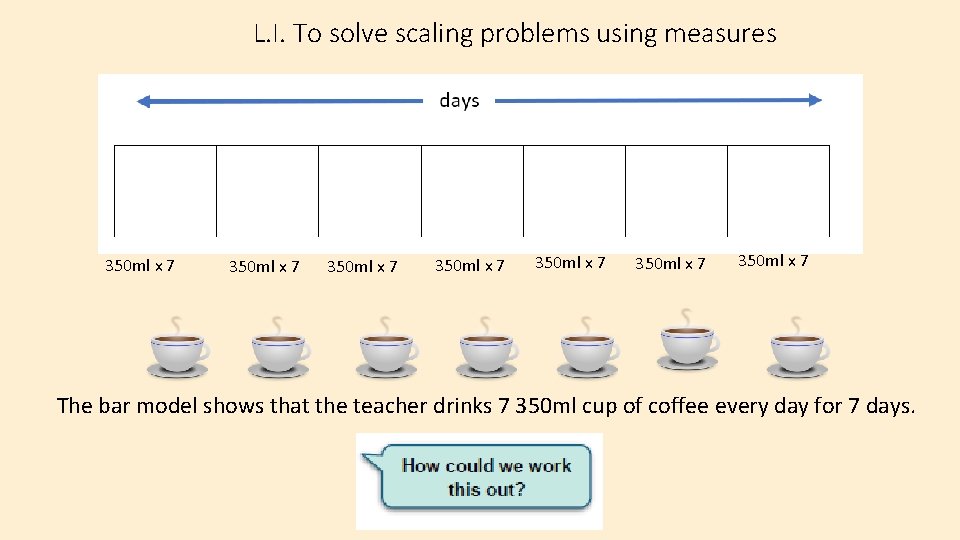
L. I. To solve scaling problems using measures 350 ml x 7 350 ml x 7 The bar model shows that the teacher drinks 7 350 ml cup of coffee every day for 7 days.

L. I. To solve scaling problems using measures Possible strategies…. 1) You could calculate how many ml of coffee the teacher drank in one day and then convert the answer to litres. Then multiply the answer by 7 (to work out how much they drank in 7 days) 2) You could start by converting 350 ml into litres and then multiply the answer by 49 (7 cups x 7 days) Which strategy do you prefer? Let’s see what both of these strategies look like…

L. I. To solve scaling problems using measures Possible strategies…. 1) You could calculate how many ml of coffee the teacher drank in one day and then convert the answer to litres. Then multiply the answer by 7 (to work out how much they drank in 7 days) 3 In one day: 350 x 7 = X 2, 450 ml = 2. 45 L 3 2. 4 1 7. 1 5 7 5 The reason for converting from ml to litres is that it made the last multiplication sum easier because the numbers were smaller.

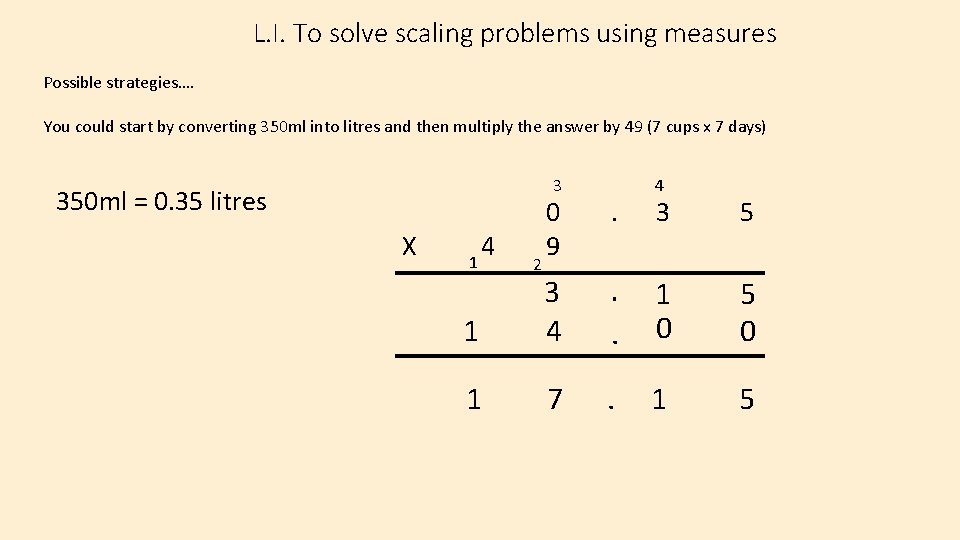
L. I. To solve scaling problems using measures Possible strategies…. You could start by converting 350 ml into litres and then multiply the answer by 49 (7 cups x 7 days) 3 350 ml = 0. 35 litres X 4 0 9 . 3 5 1 3 4 . 1. 0 5 0 1 7 . 1 5 1 4 2

L. I. To solve scaling problems using measures Give this a go. Hint: I would convert 5000 ml into litres first. The heart pumps about 5000 ml of blood in a minute. How much blood would it pump in 1 hour?

L. I. To solve scaling problems using measures The heart pumps about 5000 ml of blood in a minute. How much blood would it pump in 1 hour? Step one I converted 5000 ml into 5 litres because 5 is a smaller number and therefore easier to multiply with. 5000 ml = 5 litres Step two I converted 1 hour into 60 minutes Step three I knew that I had to multiply 5 litres by 60 minutes. I used my times table facts (5 x 6 = 30) to help me. I remembered that I needed to multiply the answer by 10 because 60 is 10 x bigger than 6. 5 x 60 = (5 x 6) x 10 = 300 litres of blood an hour

L. I. To solve scaling problems using measures How would you solve this problem? Hint: you are going to need to convert from metres to kilometres at some point because the question is asking you how many kilometres she travelled. Give this question a go. On the next slides, I will model different approaches to the problem but I would like you to attempt it first.

L. I. To solve scaling problems using measures Method #1 First I will work out how many metres she travelled in 1 hop. Then I will work out how many metres she travelled in 125 hops. I’ll convert my answer to kilometres at the end.

L. I. To solve scaling problems using measures Method #1 40 hops = 10 metres 1 hop = 0. 25 metres I divided 40 hops by 40 to get 1 hop. I divided 10 metres by 40 to get 0. 25 metres. (To do this, I knew that 10 ÷ 4 = 2. 5 therefore 10 ÷ 40 = 0. 25)

L. I. To solve scaling problems using measures Method #1 125 x 0. 25 m = 31. 25 m When we multiply by whole number by a decimal, the answer is going to be smaller than the number we started on because we are multiplying by a number that is smaller than one (the decimal) A handy tricky/hack is to use your knowledge of fraction/decimal equivalents. 0. 25 = ¼ so when we multiply by 0. 25, we are basically just finding ¼ of the whole number. 125 divided by 4 = 31. 25 Or 125 divided by 2 = 62. 5; 62. 5 divided by 2 = 31. 25

L. I. To solve scaling problems using measures Method #1 31. 25 m = 0. 03125 km

L. I. To solve scaling problems using measures Method #2 We know that at some point we are going to need to convert from metres to kilometres because the question is asking how many kilometres she travelled, not metres. Looking at the numbers in the question, I’m going to choose to not convert 10 m into kilometres because working with the number 10 is easy. Using my 4 x times table facts, I know that 4 x 3 = 12; therefore, 40 x 3 = 120. I can use this to work out how many metres she travels after 120 hops. Draw a bar model to represent how many metres she travels in 120 hops.

L. I. To solve scaling problems using measures 10 m 10 m 40 hops 30 m 120 hops So we now know that Val travelled 30 m after 120 hops; however, the question asked us how far she travelled after 125 hops. How can we use what we already know to work out how many metres she travelled in 5 hops?

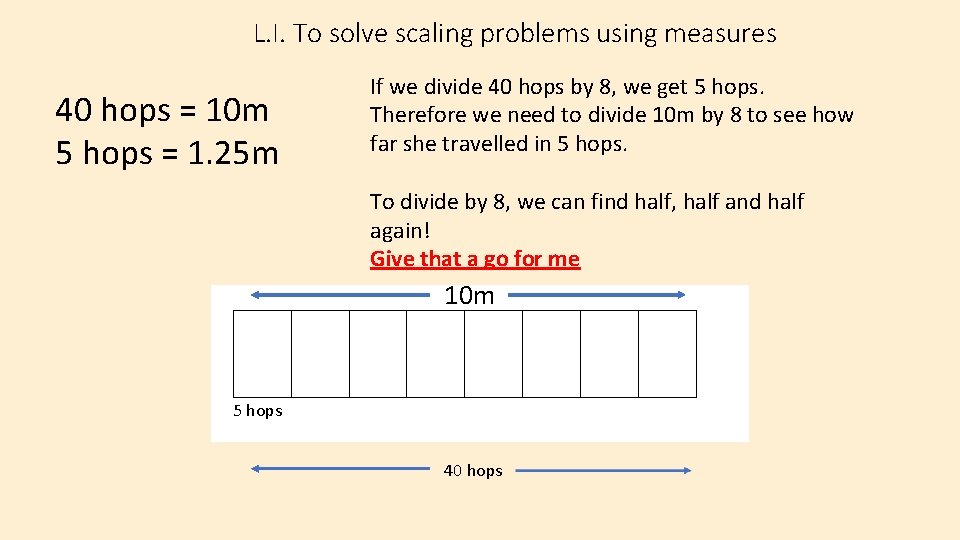
L. I. To solve scaling problems using measures 40 hops = 10 m 5 hops = 1. 25 m If we divide 40 hops by 8, we get 5 hops. Therefore we need to divide 10 m by 8 to see how far she travelled in 5 hops. To divide by 8, we can find half, half and half again! Give that a go for me 10 m 5 hops 40 hops

L. I. To solve scaling problems using measures ½ of 10 = 5 ½ of 0. 5 = 2. 5 ½ of 0. 25 = 1. 25 An easy way to do this is to follow the same pattern but starting with 100: ½ of 100 = 50 ½ of 50 = 25 ½ of 25 = 12. 5 Just remember to divide the answer by 10!

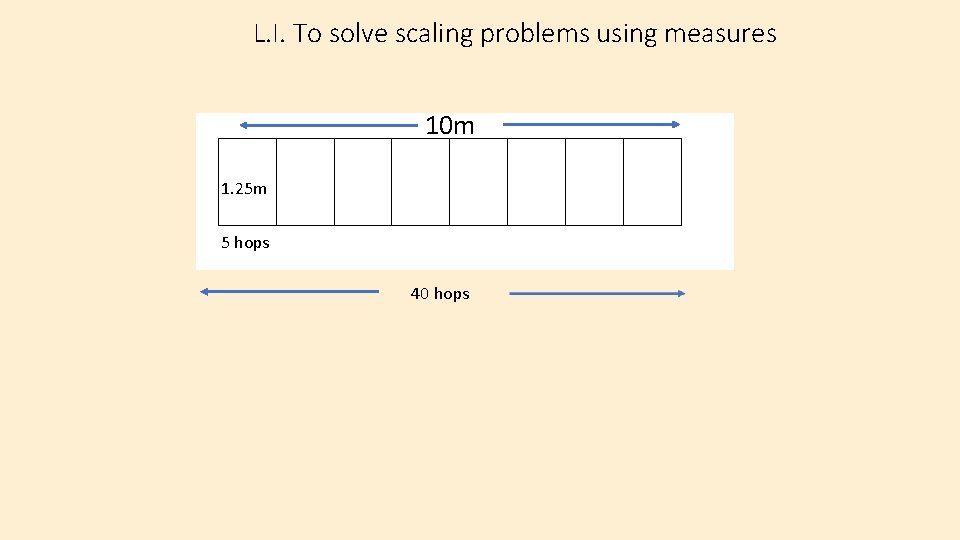
L. I. To solve scaling problems using measures 10 m 1. 25 m 5 hops 40 hops

L. I. To solve scaling problems using measures 10 m 40 hops Now add up the number of metres. Then convert metres to kilometres. 10 m 40 hops 1. 25 m 5 hops 31. 25 m = 0. 03125 km

L. I. To solve scaling problems using measures Ultimately it doesn’t matter which strategy you use; the best strategy is the one that makes the most sense to you and is as efficient as possible. Give this question a go for me. Look at the numbers carefully to decide whether you will convert the units of measure at the beginning or the end of your strategy. Draw a bar model but only if it helps! Answer is on the next page. Greater depth Explain your reasoning for when you chose to convert from centimetres to metres.

L. I. To solve scaling problems using measures Greater depth Explain your reasoning for when you chose to convert from centimetres to metres. 0. 72 m 6 copies = 7. 2 cm 60 is 10 x than 6. 7. 2 x 10 = 72 cm = 0. 72 m If I converted 7. 2 cm to metres, I would have to divide it by 100. 7. 2 ÷ 100 = 0. 072. This is a difficult number to multiply. It was easier to convert from cm to m at the end of this problem because the number was a whole number rather than a decimal.

L. I. To solve scaling problems using measures.