L 23 Adder Architectures Adders o Carry Lookahead
















- Slides: 21

L 23 – Adder Architectures

Adders o Carry Lookahead adder Carry select adder (staged) Carry Multiplexed Adder o Ref: text Unit 15 o o 9/2/2012 – ECE 3561 Lect 9 Copyright 2012 - Joanne De. Groat, ECE, OSU 2

The carry lookahead adder o The generation of all outputs is a direct function of the inputs. n n o The carry out is a function of all inputs. The msb sum output is also a function of all inputs. Time of addition is the shortest. 9/2/2012 – ECE 3561 Lect 9 Copyright 2012 - Joanne De. Groat, ECE, OSU 3

The equations o o o Create two signals called propagate and generate, Pi and Gi Pi (A, B) = Ai + Bi or Ai Å Bi Gi (A, B) = Ai· Bi G is the generate function – when both A and B are a 1, there is a carry generated P is the propagate function – when a 1 it will propagate the carry in. n When both inputs are 1, the G function generates a carry so either form of the P function works. 9/2/2012 – ECE 3561 Lect 9 Copyright 2012 - Joanne De. Groat, ECE, OSU 4

The equations o o o o C 1 = G 0 + P 0 C 2 = G 1 + P 1 C 2 = G 1 + G 0 P 1 + C 0 P 1 C 3 = G 2 + P 2 C 3 = G 2 + G 1 P 2 + G 0 P 1 P 2 + C 0 P 1 P 2 C 4 = G 3 + P 3 C 4 = G 3 + G 2 P 3 + G 1 P 2 P 3 + G 0 P 1 P 2 P 3 + C 0 P 1 P 2 P 3 9/2/2012 – ECE 3561 Lect 9 Copyright 2012 - Joanne De. Groat, ECE, OSU 5

And the sum output o o o The sum is the conventional equation Sum (i) = A(i) Å B(i) Å C(i) If the XOR form of propagate is used Sum (i) = P(i) Å C(i) Note on CLA – the logic required to implement it exponentially increases with the number of bits to be added. 9/2/2012 – ECE 3561 Lect 9 Copyright 2012 - Joanne De. Groat, ECE, OSU 6

The VHDL – 4 -bit carry lookahead o ENTITY cla IS PORT (a, b : IN bit_vector (3 downto 0); cin : IN bit; sum : OUT bit_vector (3 downto 0); cout : OUT bit); END cla; ARCHITECTURE one OF cla IS SIGNAL P, G : bit_vector (3 downto 0); SIGNAL C : bit_vector (4 downto 0); BEGIN P <= A OR B; G <= A AND B; C(0) <= cin; C(1) <= G(0) OR (P(0) AND C(0)); C(2) <= G(1) OR (G(0) AND P(1)) OR (C(0) AND P(1)); C(3) <= G(2) OR (G(1) AND P(2)) OR (G(0) AND P(1) AND P(2)) OR (C(0) AND P(1) AND P(2)); C(4) <= G(3) OR (G(2) AND P(3)) OR (G(1) AND P(2) AND P(3)) OR (G(0) AND P(1) AND P(2) AND P(3)) OR (C(0) AND P(1) AND P(2) AND P(3)); sum <= P XOR C(3 downto 0); END one; 9/2/2012 – ECE 3561 Lect 9 Copyright 2012 - Joanne De. Groat, ECE, OSU 7

And the synthesis o Resources used n n Combinational LUTs – 8 Pins - 14 9/2/2012 – ECE 3561 Lect 9 Copyright 2012 - Joanne De. Groat, ECE, OSU 8

Growth of LUTs o For a 6 bit unit n n n n C 5 = G 4 + P 4 C 5 = G 4 + G 3 P 4 + G 2 P 3 P 4 + G 1 P 2 P 3 P 4 + G 0 P 1 P 2 P 3 P 4 + C 0 P 1 P 2 P 3 P 4 C 6 = G 5 + P 5 C 6 = G 5 + G 4 P 5 + G 3 P 4 P 5 + G 2 P 3 P 4 P 5 + G 1 P 2 P 3 P 4 P 5 + G 0 P 1 P 2 P 3 P 4 P 5 + C 0 P 1 P 2 P 3 P 4 P 5 9/2/2012 – ECE 3561 Lect 9 Copyright 2012 - Joanne De. Groat, ECE, OSU 9

When done for a 5 -bit adder o Resources n n LUTs – 12 Pins - 71 9/2/2012 – ECE 3561 Lect 9 Copyright 2012 - Joanne De. Groat, ECE, OSU 10

And for a 6 -bit CLA o Resources n n LUTs – 17 Pins – 20 9/2/2012 – ECE 3561 Lect 9 Copyright 2012 - Joanne De. Groat, ECE, OSU 11

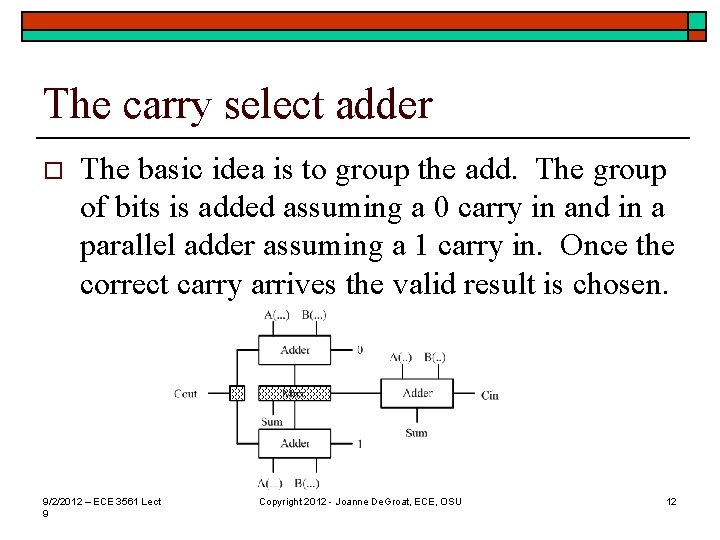
The carry select adder o The basic idea is to group the add. The group of bits is added assuming a 0 carry in and in a parallel adder assuming a 1 carry in. Once the correct carry arrives the valid result is chosen. 9/2/2012 – ECE 3561 Lect 9 Copyright 2012 - Joanne De. Groat, ECE, OSU 12

Carry select metrics o o o Speed is better than ripple carry adder but only by the staging factor. Area growth is linear and a constant factor more than ripple. Will see this at end of lecture. 9/2/2012 – ECE 3561 Lect 9 Copyright 2012 - Joanne De. Groat, ECE, OSU 13

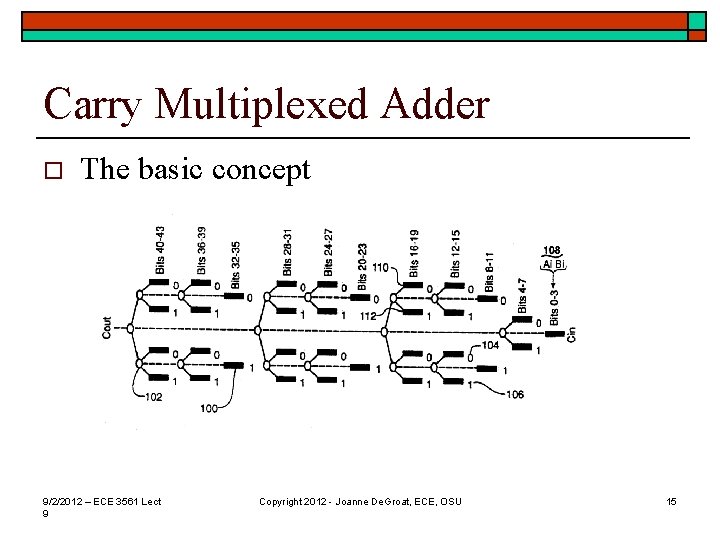
The Carry Multiplexed adder o An extension of the Carry select n n n Speed is on the order of full carry lookahead # gates used is linear growth and ~3 x that of a ripple adder of the same bit with. As speed is about as fast as the add can be completed and growth is linear this area has the best area time metric of all adders. This is the adder architecture used in all modern computer architectures. 24 patents exist for CMA architectures. 9/2/2012 – ECE 3561 Lect 9 Copyright 2012 - Joanne De. Groat, ECE, OSU 14

Carry Multiplexed Adder o The basic concept 9/2/2012 – ECE 3561 Lect 9 Copyright 2012 - Joanne De. Groat, ECE, OSU 15

Goals in the CMA o No redundant operations. 9/2/2012 – ECE 3561 Lect 9 Copyright 2012 - Joanne De. Groat, ECE, OSU 16

Moving to higher order o Still just add twice – presumed 0 and 1 9/2/2012 – ECE 3561 Lect 9 Copyright 2012 - Joanne De. Groat, ECE, OSU 17

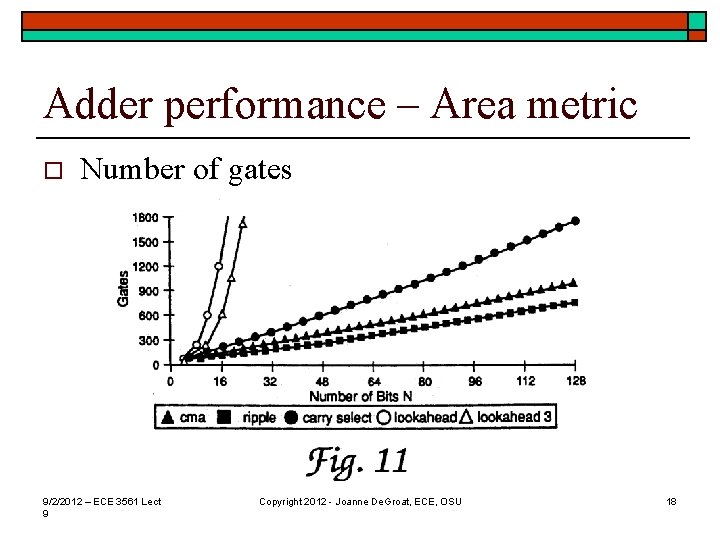
Adder performance – Area metric o Number of gates 9/2/2012 – ECE 3561 Lect 9 Copyright 2012 - Joanne De. Groat, ECE, OSU 18

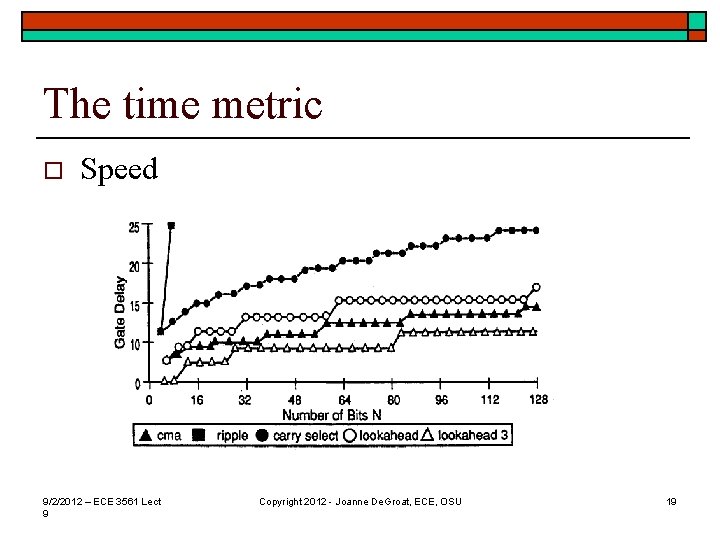
The time metric o Speed 9/2/2012 – ECE 3561 Lect 9 Copyright 2012 - Joanne De. Groat, ECE, OSU 19

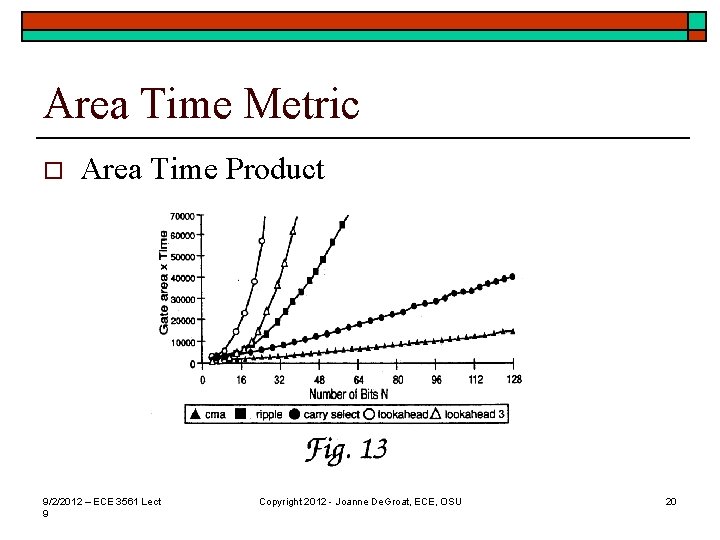
Area Time Metric o Area Time Product 9/2/2012 – ECE 3561 Lect 9 Copyright 2012 - Joanne De. Groat, ECE, OSU 20

Lecture summary o The adder was a simple ripple carry adder. o Other Architectures n n n Carry Lookahead Carry select Carry multiplexed 9/2/2012 – ECE 3561 Lect 9 Copyright 2012 - Joanne De. Groat, ECE, OSU 21