L 2 STE 1 Plan Intervalles de confiance

L 2 STE 1

Plan Intervalles de confiance & tests statistiques • Echantillonnage, rappels • Intervalle de confiance Moyenne Variance et écart type Médiane Pourcentage • Tests usuels Principe (rappels) Théorie de la statistique de décision (rappels) Comparaison de deux moyennes expérimentales (grands et petits échantillons) Comparaison de moyennes de deux échantillons appariés Comparaison de deux fréquences expérimentales Comparaison de deux variances expérimentales • Tests non-paramétriques Conditions d’utilisation Utilisation des rangs Test de signe Test U de Mann-Whitney Test de Wilcoxon Test de Kolmogorov-Smirnov 11/2/2020 Statistiques 2

Echantillonnage – Estimation d’un paramètre Extraction de n échantillons d’une population P Si l’on extrait plusieurs échantillons représentatifs de taille n fixée, les différences observées entre les résultats obtenus sont dues à des fluctuations d’échantillonnage. A partir d’un échantillon, on n’a donc pas de certitudes mais des estimations de paramètres. L'estimation d'un paramètre peut être faite - par un seul nombre: estimation ponctuelle - par 2 nombres entre lesquels le paramètre peut se trouver: estimation par intervalle 3

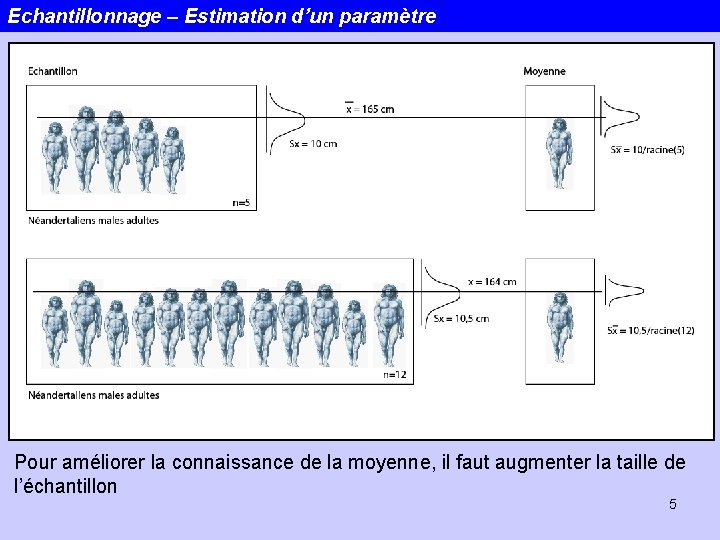
Echantillonnage – Estimation d’un paramètre Estimation ponctuelle d’une moyenne x barre Estimateur sans biais Ecart type de la moyenne 4

Echantillonnage – Estimation d’un paramètre Pour améliorer la connaissance de la moyenne, il faut augmenter la taille de l’échantillon 5

Echantillonnage – Estimation d’un paramètre Intervalle de confiance de la moyenne Cas des grands échantillons (variance connue): Soit une population obéissant à une loi normale de moyenne m et d’écart type s. 6

Echantillonnage – Estimation d’un paramètre Exemple: 45 hommes de Neandertal males adultes à 95% de confiance 7

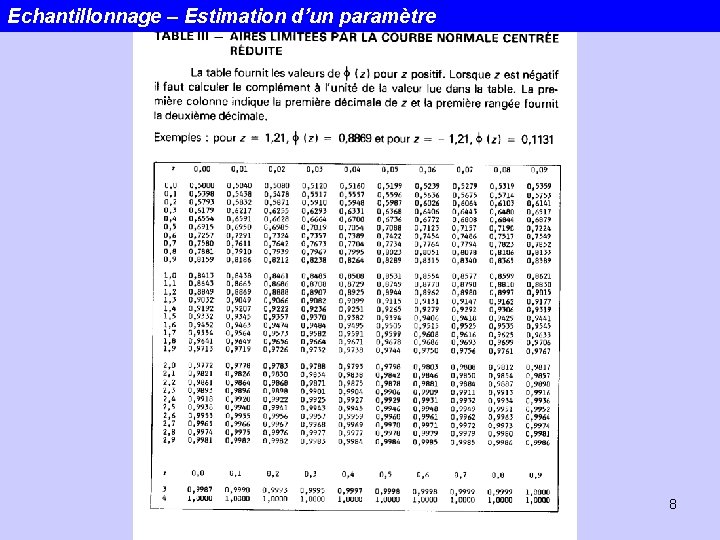
Echantillonnage – Estimation d’un paramètre 8

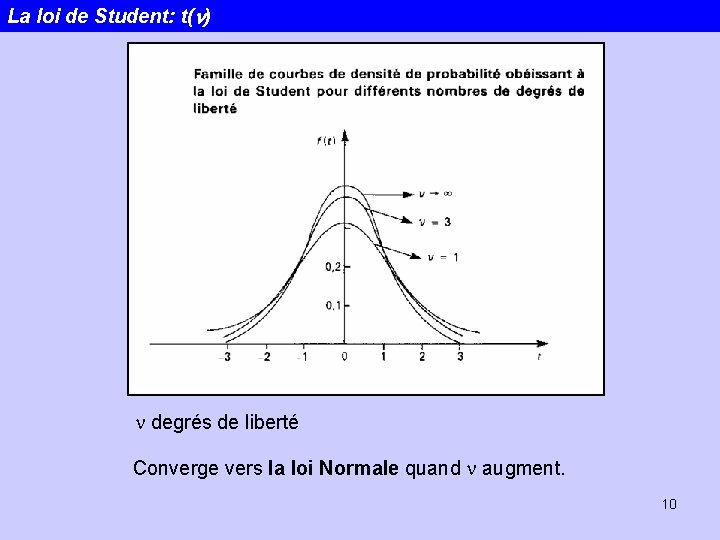
Echantillonnage – Estimation d’un paramètre Intervalle de confiance de la moyenne Cas des petits échantillons: Quand n<30 ou quand la variance est inconnue, on prend la loi de Student. Pour n = n-1 degrés de liberté Finalement on peut toujours utiliser la loi de Student puisque t tend vers la loi normale quand n est grand… 9

La loi de Student: t(n) n degrés de liberté Converge vers la loi Normale quand n augment. 10

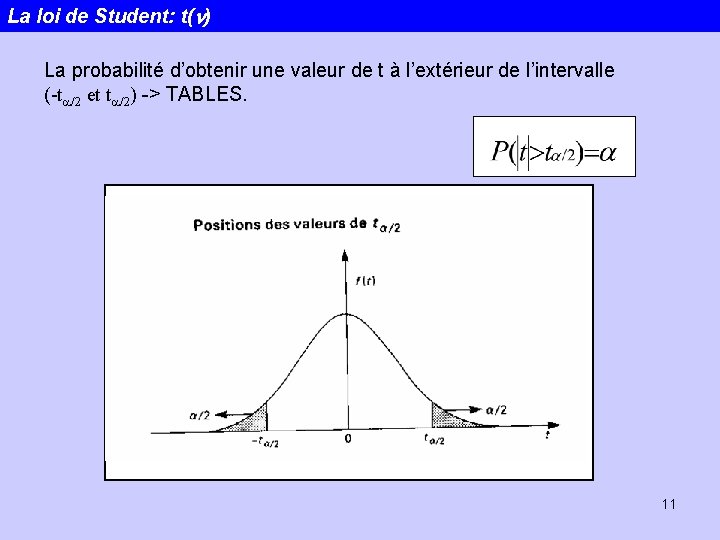
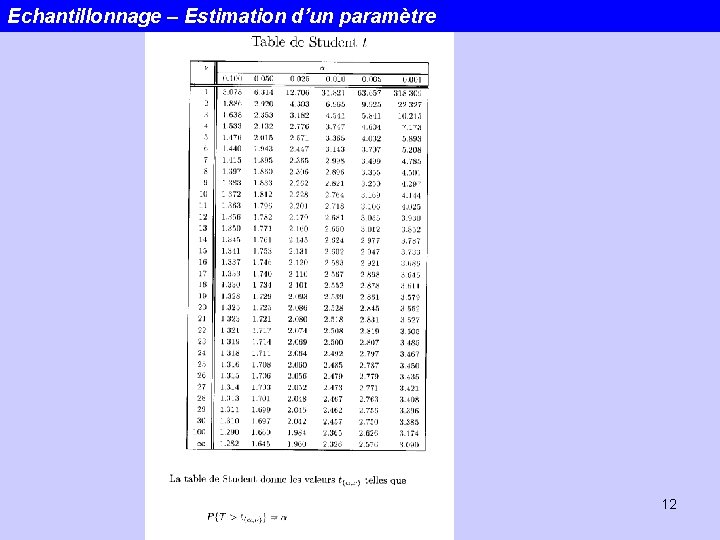
La loi de Student: t(n) La probabilité d’obtenir une valeur de t à l’extérieur de l’intervalle (-ta/2 et ta/2) -> TABLES. 11

Echantillonnage – Estimation d’un paramètre 12

Echantillonnage – Estimation d’un paramètre Exemple: 6 hommes de Neandertal males adultes à 95% de confiance Finalement on peut toujours utiliser la loi de Student puisque t tend vers la loi normale quand n est grand… 13

Echantillonnage – Estimation d’un paramètre Intervalle de confiance de la variance Soit une population obéissant à une loi normale de moyenne m (inconnue) et d’écart type s (inconnu). Pour n = n-1 degrés de liberté 14

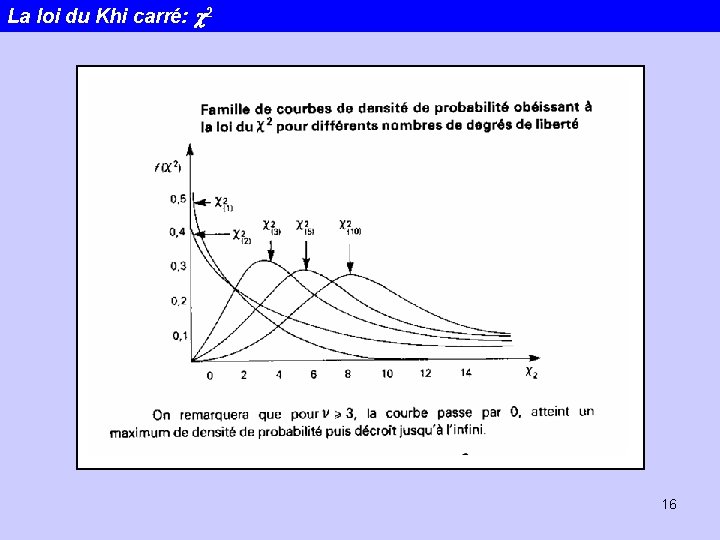
La loi du Khi carré: c 2 Si Z 1, Z 2, Zn sont des variables aléatoires normales centrées réduites et indépendantes entres elles, la somme des carrées de ces varaibles aléatoires obéit à la loi du c 2 à n degrés de libertés 15

La loi du Khi carré: c 2 16

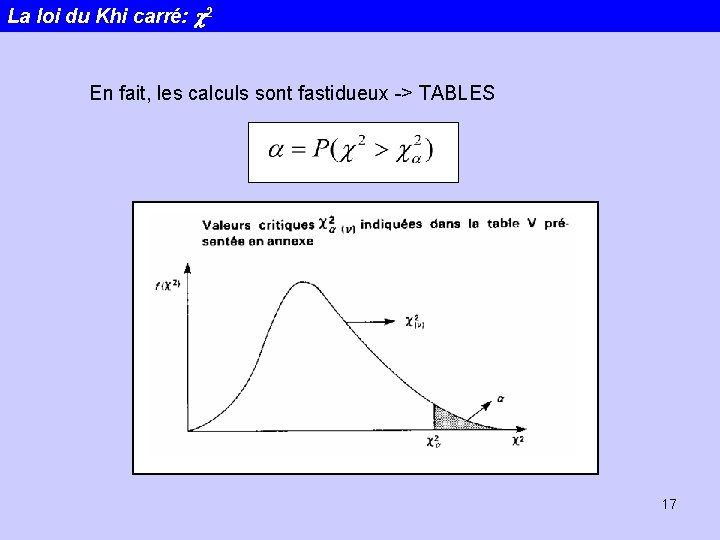
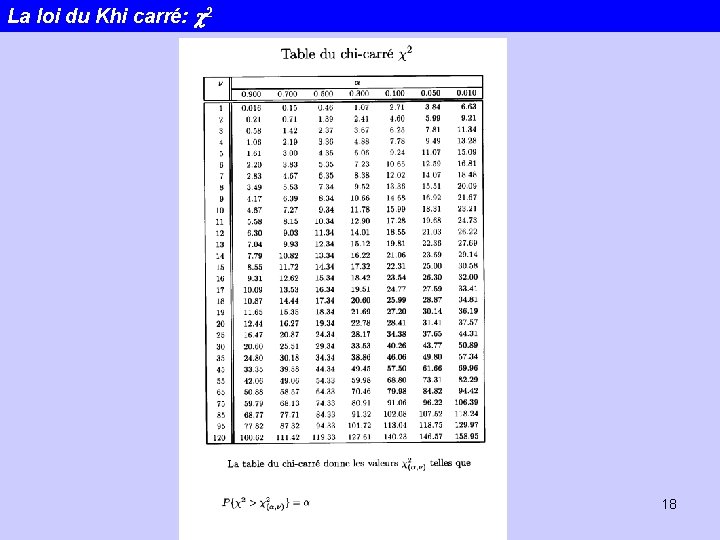
La loi du Khi carré: c 2 En fait, les calculs sont fastidueux -> TABLES 17

La loi du Khi carré: c 2 18

Echantillonnage – Estimation d’un paramètre Intervalle de confiance de l’écart type (idem) Soit une population obéissant à une loi normale de moyenne m et d’écart type s. Pour n = n-1 degrés de liberté 19

Echantillonnage – Estimation d’un paramètre Intervalle de confiance de la médiane Si un échantillon est extrait d’une population approximativement normale, et si son effectif est relativement grand (n>60), la distribution d’échantillonnage de la médiane s’approche de la loi normale. 20

Echantillonnage – Estimation d’un paramètre Estimation ponctuelle d’un pourcentage La population est formée d’individus ayant ou non un caractère A. Soit p la probabilité pour qu’un individu pris au hasard dans la population présente le caractère A. Quand on dispose d’un seul échantillon de taille n, la meilleure estimation ponctuelle de P est donc la fréquence p observée sur l’échantillon. 21

Echantillonnage – Estimation d’un paramètre Intervalle de confiance d’un pourcentage Grands échantillons (n>30), p ni voisin de 0, ni voisin de 1, (np>5, n(1 p)>5) La variable fréquence obéit à une loi normale centrée réduite 22

Echantillonnage – Estimation d’un paramètre Un problème très fréquent! Un quotidien publie tous les mois la cote du chef du gouvernement à partir d'un sondage réalisé sur un échantillon représentatif de 1000 personnes. En janvier, la cote publiée était de 38% d'opinions favorables, en février de 36%. Un journaliste commente alors ces valeurs par "Le chef du gouvernement perd 2 points !!" En fait: On construit un intervalle de confiance autour des proportions. Avec un seuil de 95%, on obtient respectivement [35; 41] et [33; 39] pour les valeurs 38% et 36%. Les deux intervalles ayant une intersection non vide, on ne peut pas conclure qu'il y ait eu baisse ou augmentation de la cote du chef de gouvernement. 23

L 2 STE 24

Théorie de la statistique de décision Quel est le problème…? On sait qu’un homme de Neandertal mesure en moyenne 165 cm. Sur un site on trouve 16 hommes avec une moyenne de 167 et un écart type de 8 cm (e. t. échantillon). Comparaison de la moyenne avec la valeur théorique de 165 cm Possibilités: Moyenne très élevée: Nous pourrons être amenés à croire que ces hommes ont des tailles différentes de 165 cm Moyenne faiblement plus élevée: on ne pourra pas conclure si c’est significativement supérieur à la norme ou si c’est l’effet du hasard. 25

Théorie de la statistique de décision Question: à partir de quelle limite pouvons nous raisonnablement conclure à une différence? H 0: m=165 (il n’y pas de différence) H 1: m≠ 165 Calcul de Sur la table la probabilité pour que la moyenne d’échantillonnage soit différente celle de la population de plus 2, 131 de écart-type est de 5%. 26

Théorie de la statistique de décision Les deux risques d’erreur dans un test. Erreur de 2 nde espèce (compliquée) 1 -a 1 -b Erreur de 1 ere espèce A priori on ne sait pas à quel type d’erreur on sera confronté: Le résultat de l’échantillon a révélé 167 cm probablement par pur hasard. On conclue que la moyenne pourrait être 165 cm alors qu’en fait elle est mesurée à 167 cm. 27

Théorie de la statistique de décision H 0 : hypothèse nulle ou principale Ex: Les haches de type A présentent les mêmes teneurs en Sn que les haches de type B. H 1 : hypothèse alternative ou contraire … Soumission à une épreuve de vérité! Conclusion : différence attribuable aux fluctuations d’échantillonnage? ? ? 28

Théorie de la statistique de décision Niveau de signification : un peu arbitraire… significatif : 0. 05 hautement significatif : 0. 01 très hautement significatif : 0. 001. Test bilatéral / unilatéral : bilatéral : différence sans se préoccuper du sens. Unilatéral : > ou <. Zone de rejet d’un seul coté de la distribution de probabilité de référence. Echantillons indépendants ou appariés: Indépendants : aucune influence du 1 er ech sur le 2 nd. Appariés : prélèvements par paires. Ex : fumeurs H + F. 29

Comparaison de deux moyennes expérimentales–grands échantillons Comparaison des moyennes de 2 grands échantillons indépendants (n 1 et n 2 >30): Deux échantillons qui suivent des lois normales: m 1, s 21; m 2, s 22 H 0 : m 1 = m 2 Si H 0 est vraie, Zc suit une loi normale N(0, 1) 30

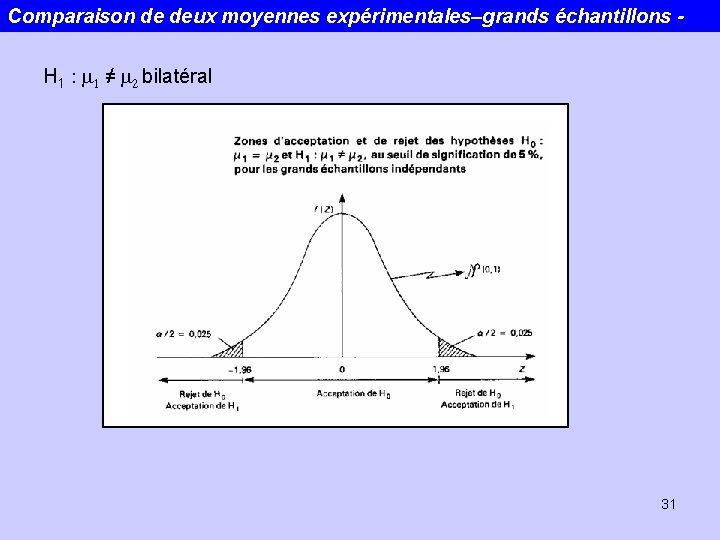
Comparaison de deux moyennes expérimentales–grands échantillons H 1 : m 1 ≠ m 2 bilatéral 31

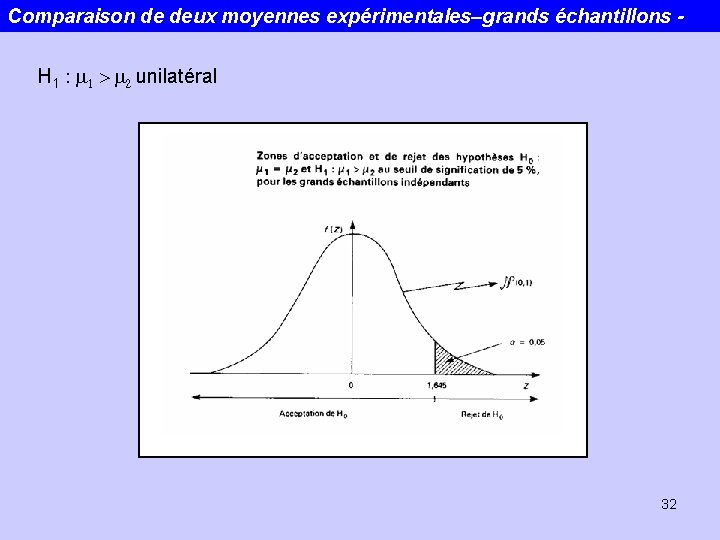
Comparaison de deux moyennes expérimentales–grands échantillons H 1 : m 1 > m 2 unilatéral 32

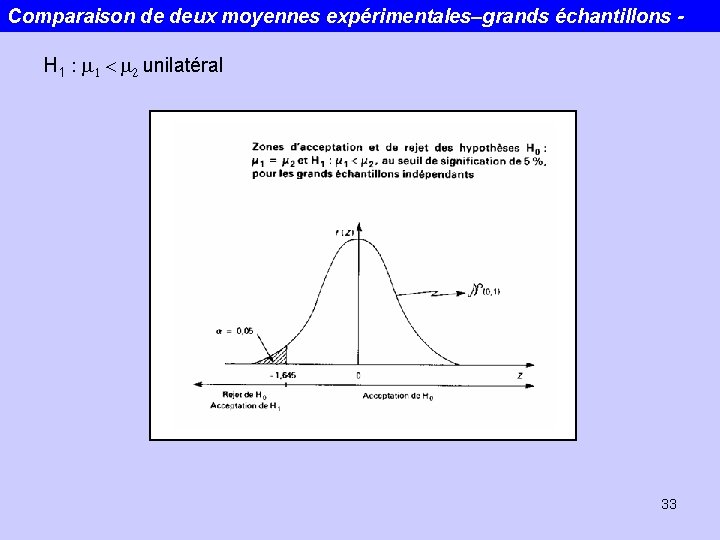
Comparaison de deux moyennes expérimentales–grands échantillons H 1 : m 1 < m 2 unilatéral 33

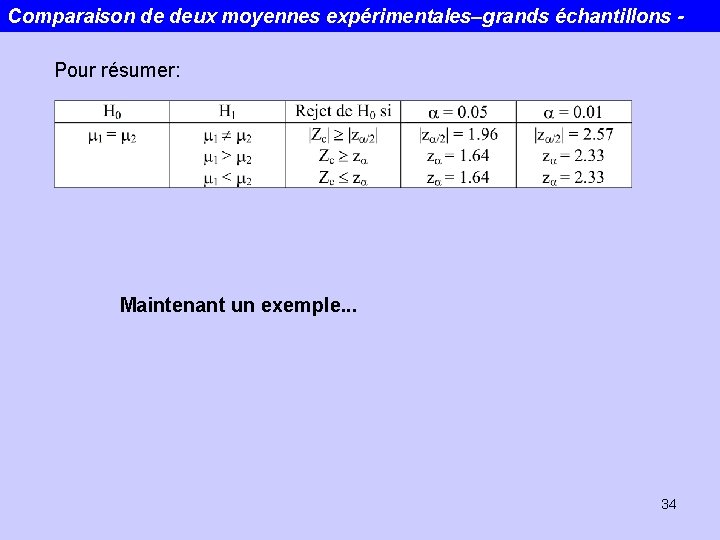
Comparaison de deux moyennes expérimentales–grands échantillons Pour résumer: Maintenant un exemple. . . 34

Comparaison de deux moyennes expérimentales–grands échantillons Taille des silex sur deux sites Les moyennes de ces deux échantillons prélevés indépendamment l’un de l’autre diffèrent-elles d’une façon hautement significative? 35

Comparaison de deux moyennes expérimentales–grands échantillons - n 1 et n 2 grands -> test sur la loi normale H 0 : ma = mb H 1 : ma mb (bilatéral) a = 0. 01, Za/2 = 2. 57 36

Comparaison de deux moyennes expérimentales–grands échantillons - H 0 rejetée au seuil de signification de 1% 37

Comparaison d’une moyenne empirique à une moyenne théorique Même principe que précédemment (quand n est grand): H 0: m=m 0 que l’on teste sur la loi normale N(0, 1) 38

Comparaison de deux moyennes expérimentales– petits échantillons Cas des petits échantillons: Test t Deux populations normales m 1 et m 2 de même variance (au moins approximativement) s 2. Si n 1 et n 2 sont petits, s 2 x 1 et s 2 x 2 sont des estimateurs peu précis de s 2. Dans ce cas, la variable différence centrée réduite n’obéit plus à une loi normale mais à une loi de Student à n=n 1+n 2 -2 degrés de liberté. 39

Comparaison de deux moyennes expérimentales– petits échantillons La variance de la distribution des différences de moyennes estimées par s 2 D avec 40

Comparaison de deux moyennes expérimentales– petits échantillons Ce qui donne… H 0 : ma = mb Avec n = n 1 + n 2 - 2 41

Comparaison de deux moyennes expérimentales– petits échantillons Si les variances s’avèrent inégales alors test t modifié. avec 42

Comparaison d’une moyenne empirique à une moyenne théorique Même principe que précédemment. Suivant si n est petit ou grand, on calcule les variables auxiliaires suivantes: H 0: m=m 0 que l’on teste sur la loi de Student ou loi normale N(0, 1) 43

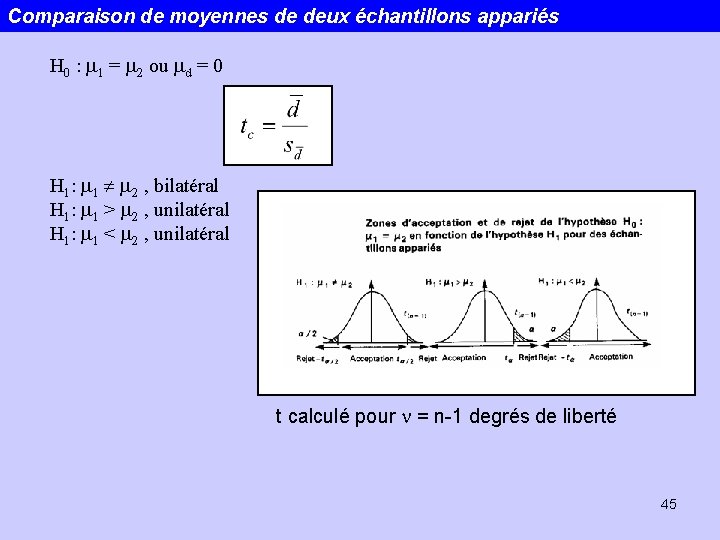
Comparaison de moyennes de deux échantillons appariés Fondée sur les différences de chaque paire d’éléments On imagine que la différence obéit à une loi normale, mais en général on utilise une loi de Student à n-1 degrés de liberté: 44

Comparaison de moyennes de deux échantillons appariés H 0 : m 1 = m 2 ou md = 0 H 1: m 1 m 2 , bilatéral H 1: m 1 > m 2 , unilatéral H 1: m 1 < m 2 , unilatéral t calculé pour n = n-1 degrés de liberté 45

Comparaison de deux fréquences expérimentales Comparaison des fréquences de 2 grands échantillons indépendants. Deux échantillons : f 1, n 1; f 2, n 2 On approxime la loi binomiale par la loi normale mais: n 1>30, n 2>30, n 1 f 1>5, n 2 f 2>5, n 1(1 -f 1)>5, n 2(1 -f 2)>5 H 0 : p 1 = p 2 = p 46

Comparaison de deux fréquences expérimentales Sous H 0 on peut réunir les deux échantillons, et on est conduit à l’estimation de p Zc devient H 1: p 1≠p 2 H 1: p 1>p 2 H 1: p 1<p 2 Test sur la loi normale N(0, 1) 47

Comparaison d’une fréquence empirique et d’une fréquence théorique La différence entre f (mesuré) et p (théorique) est-elle seulement explicable par les aléas dus à l’échantillonnage? On approxime la loi binomiale par la loi normale mais: n>30, np>5 et nq>5 H 0 : f = p H 1: f≠p H 1: f>p H 1: f<p Test sur la loi normale N(0, 1) 48

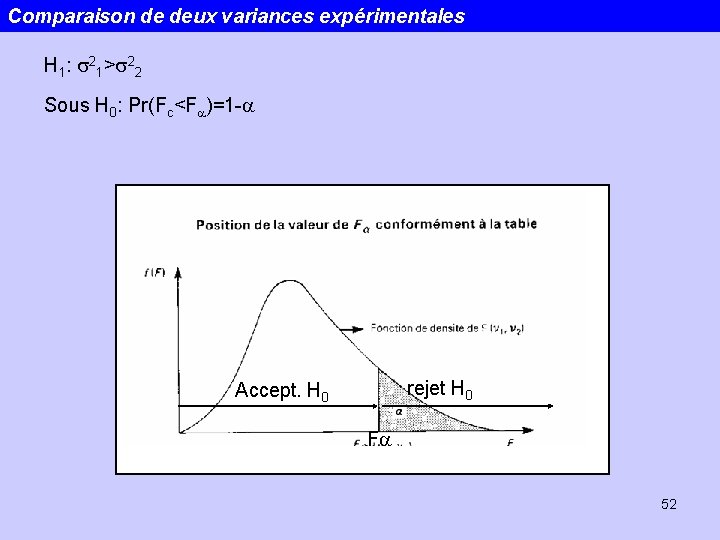
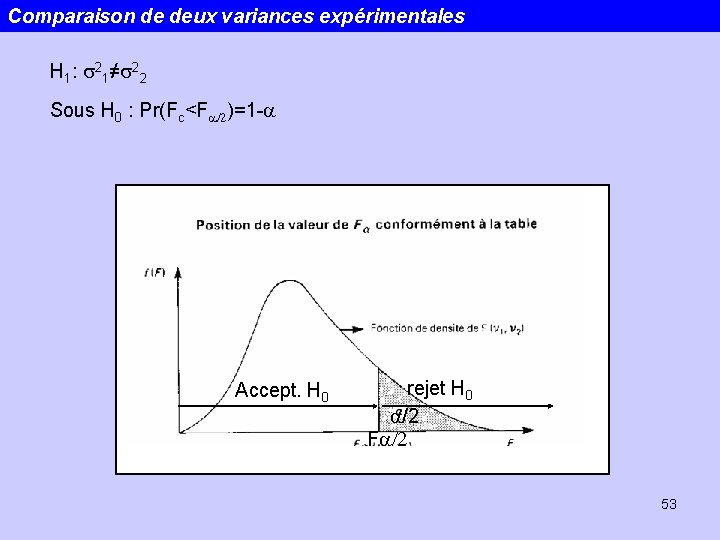
Comparaison de deux variances expérimentales Deux échantillons qui suivent des lois normales: m 1, s 21; m 2, s 22 Plus grande variance H 0: s 21=s 22 calcul de : >1 Plus petite variance Si H 0 est vraie, Fc suit une loi de Fisher-Snedecor avec n 1=n 1 -1 et n 2=n 2 -1 49

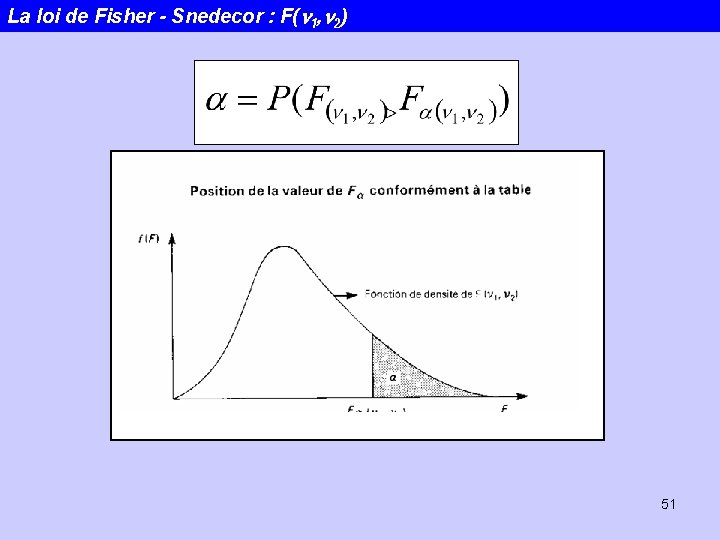
La loi de Fisher - Snedecor : F(n 1, n 2) Soit c 21 et c 22, un couple de variables aléatoires indépendantes suivant respectivement des lois du c 2 à n 1 et n 2 degrés de libertés. Utile pour les tests de variance et de covariance 50

La loi de Fisher - Snedecor : F(n 1, n 2) 51

Comparaison de deux variances expérimentales H 1: s 21>s 22 Sous H 0: Pr(Fc<Fa)=1 -a rejet H 0 Accept. H 0 Fa 52

Comparaison de deux variances expérimentales H 1: s 21≠s 22 Sous H 0 : Pr(Fc<Fa/2)=1 -a Accept. H 0 rejet H 0 a/2 Fa/2 53

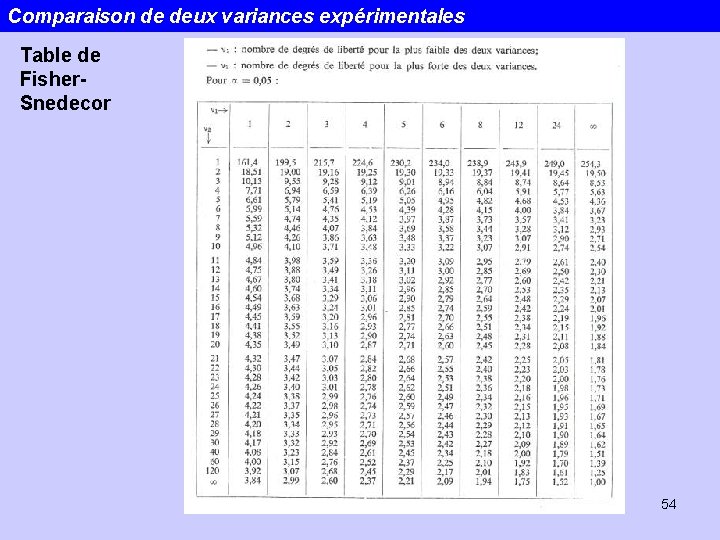
Comparaison de deux variances expérimentales Table de Fisher. Snedecor 54

11/2/2020 Statistiques 55

Plan 1. Généralités Conditions d’application Utilisation des rangs 2. Les tests: Le test de signes Le test U de Mann-Whitney Le test de Wilcoxon Le test de Kolmogorov Smirnov 11/2/2020 Statistiques 56

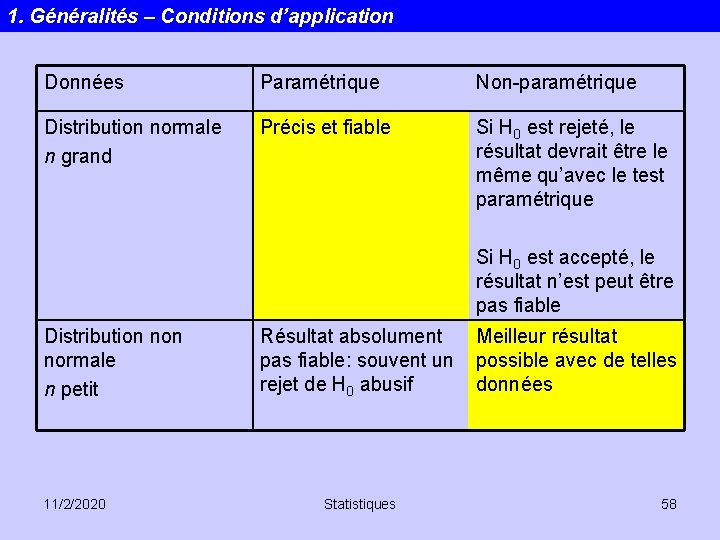
1. Généralités – Conditions d’application Pourquoi et quand utiliser des statistiques non-paramétriques? Les tests non paramétriques ne font aucune hypothèse sur la distribution sousjacente des données. On les qualifie souvent de tests distribution free. L’étape préalable consistant à estimer les paramètres distributions (p. e. moyenne et écart type) avant de procéder au test d’hypothèse proprement dit n’est plus nécessaire. Quand? : 1. L’échelle des données est ordinale plutôt que sous forme d’intervalles ou de rapports. Dans ce cas les opérations arithmétiques n’ont pas de sens! 2. Les mesures sont sur des échelles d’intervalles ou de rapports mais les distributions de fréquences observées sont très éloignées de la distribution normale. 11/2/2020 Statistiques 57

1. Généralités – Conditions d’application Données Paramétrique Non-paramétrique Distribution normale n grand Précis et fiable Si H 0 est rejeté, le résultat devrait être le même qu’avec le test paramétrique Si H 0 est accepté, le résultat n’est peut être pas fiable Distribution normale n petit 11/2/2020 Résultat absolument pas fiable: souvent un rejet de H 0 abusif Statistiques Meilleur résultat possible avec de telles données 58

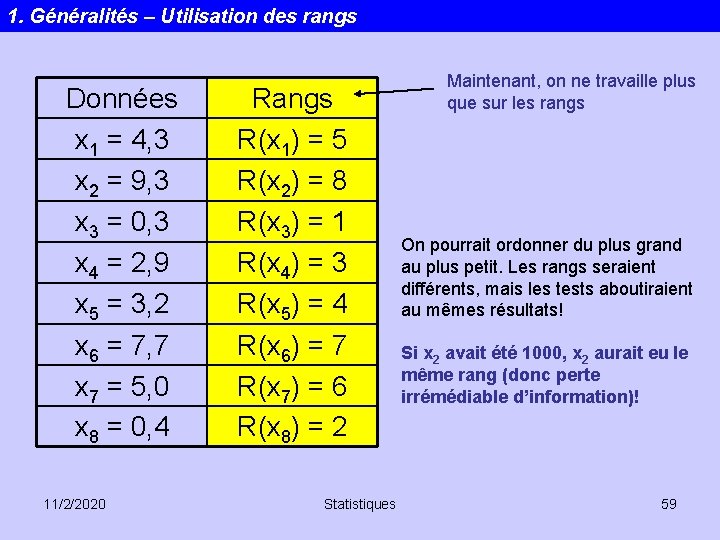
1. Généralités – Utilisation des rangs Données x 1 = 4, 3 x 2 = 9, 3 x 3 = 0, 3 x 4 = 2, 9 x 5 = 3, 2 x 6 = 7, 7 x 7 = 5, 0 x 8 = 0, 4 11/2/2020 Rangs R(x 1) = 5 R(x 2) = 8 R(x 3) = 1 R(x 4) = 3 R(x 5) = 4 R(x 6) = 7 R(x 7) = 6 R(x 8) = 2 Statistiques Maintenant, on ne travaille plus que sur les rangs On pourrait ordonner du plus grand au plus petit. Les rangs seraient différents, mais les tests aboutiraient au mêmes résultats! Si x 2 avait été 1000, x 2 aurait eu le même rang (donc perte irrémédiable d’information)! 59

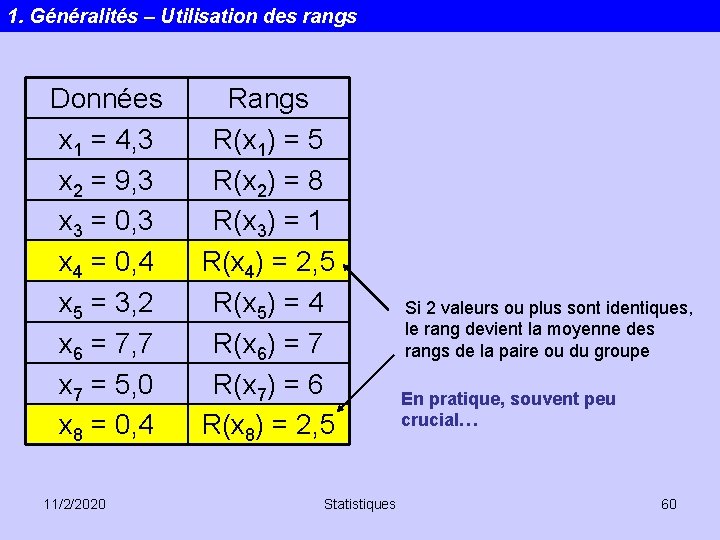
1. Généralités – Utilisation des rangs Données x 1 = 4, 3 x 2 = 9, 3 x 3 = 0, 3 x 4 = 0, 4 x 5 = 3, 2 x 6 = 7, 7 x 7 = 5, 0 x 8 = 0, 4 11/2/2020 Rangs R(x 1) = 5 R(x 2) = 8 R(x 3) = 1 R(x 4) = 2, 5 R(x 5) = 4 R(x 6) = 7 R(x 7) = 6 R(x 8) = 2, 5 Statistiques Si 2 valeurs ou plus sont identiques, le rang devient la moyenne des rangs de la paire ou du groupe En pratique, souvent peu crucial… 60

1. Généralités – Rappels sur la médiane Si n est impair: médiane = valeur du point avec le rang (n+1)/2 Si n est pair: médiane entre les valeurs des points qui ont les rangs n/2 et (n+2)/2 Valeur pour laquelle la fréquence cumulée est égale à 0. 50 ou point qui partage la distribution en 2 parties égales. Pour n impair 11/2/2020 Pour n pair Statistiques 61

2. Les tests – Le test des signes (petits échantillons) Alternative non-paramétrique au test t Cas d’un petit échantillon Voyons un exemple: ces mesures de mercure dans les sols sont-elles issues d’une population dont la médiane serait 40 ppm? Hg ppm 56 42 61 61 42 55 35 42 39 + + + - + - Signe 65 44 + + 51 32 82 41 + - + + Résultat : 3 (–) et 12 (+) Question: Est-ce significativement différent de 50% (-) et 50% (+)? Il semble qu’il y ait déséquilibre… à voir… 11/2/2020 Statistiques 62

2. Les tests – Le test des signes (petits échantillons) Imaginons que (+) soit un succès: p = 0, 5. On peut appliquer la distribution binomiale, avec x, le nombre d’apparitions, p, la probabilité de succès, n, le nombre de tentatives: Probabilité de 7 succès (ou 8) sur 15 essais = 0, 19638 Probabilité de 6 succès (ou 9) sur 15 essais = 0, 15274 Probabilité de 5 succès (ou 10) sur 15 essais = 0, 09164 Probabilité de 4 succès (ou 11) sur 15 essais = 0, 04166 La somme de ces probabilités = 0, 9648, donc plus de 95% de chances de se retrouver avec de 4 à 11 (+). 11/2/2020 Statistiques 63

2. Les tests – Le test des signes (petits échantillons) On pose les hypothèses: H 0: la médiane = 40 ppm Hg H 1: la médiane ≠ 40 ppm Hg Avec 12(+), on rejette H 0 car on a déjà plus de 96% de chances de se trouver entre 4 (+) et 11 (+) par le simple fait du hasard. On en conclue donc que la médiane de la population est significativement différente de 40 ppm de Hg. 11/2/2020 Statistiques 64

2. Les tests – Le test des signes (grands échantillons) Quand n est suffisamment grand (n>20), on peut utiliser l’approximation normale de la loi binomiale avec une correction de continuité Exemple: Durée de vie supposée d’un foret pétrolier > 250 h 271 253 264 230 216 295 198 262 211 275 288 252 282 236 294 225 291 243 284 253 272 219 224 268 + + + + + - + + + + 15(+), 9(-) H 0: médiane de la population = médiane hypothétique spécifiée H 1: médiane de la population > médiane hypothétique spécifiée Attention test unilatéral 11/2/2020 Statistiques 65

2. Les tests – Le test des signes (grands échantillons) Correction de continuité (puisque la loi binomiale est discrète alors que la loi normale est continue): Il faut retrancher 0. 5 à X si X>Np et ajouter 0. 5 à X si X<Np. Ici c’est un test unilatéral, Z 0, 05= 1, 645. Z<Z 0. 05, donc H 0 n’est pas rejetée. La publicité de la marque n’est pas justifiée!!! 11/2/2020 Statistiques 66

2. Les tests – Le test U de Mann-Whitney Alternative non-paramétrique du test t à deux échantillons. Probablement le test non-paramétrique le plus utilisé dans la littérature. Il teste l’hypothèse nulle d’égalité des médianes de populations à partir desquelles deux échantillons sont tirés. H 0: médiane de la population x = médiane de la population y H 1: médiane de la population x ≠ médiane de la population y 11/2/2020 Statistiques 67

2. Les tests – Le test U de Mann-Whitney (petits échantillons) Le plus simple: traiter un exemple Alliage A (n 1=8) Alliage B (n 2=10) 18. 3 16. 4 22. 7 17. 8 18. 9 25. 3 16. 1 24. 2 12. 6 14. 1 20. 5 10. 7 15. 9 19. 6 12. 9 15. 2 11. 8 14. 7 Etape 1: Transformation en rangs Plus petit effectif = n 1 Alliage A Alliage B 12 10 16 11 13 18 9 17 3 5 15 1 8 14 4 7 2 6 Etape 2 R 1: Somme rangs = 106 11/2/2020 R 2 : somme rangs = 65 Statistiques 68

2. Les tests – Le test U de Mann-Whitney (petits échantillons) Pour tester la différence entre les rangs, on utilise la statistique suivante. Calcul de U pour l’échantillon 1 & 2 U = min (U 1, U 2) Ici Donc U=10 11/2/2020 Statistiques 69

2. Les tests – Le test U de Mann-Whitney (petits échantillons) Si n 1 & n 2 < 20: Valeurs limites ma fournie par une table telle que sous H 0, P(U<ma)=a On rejette H 0 si U<ma Ici U<17, donc H 0 est rejeté. Il y a donc une différence significative entre les deux groupes 11/2/2020 Statistiques 70

2. Les tests – Le test U de Mann-Whitney (grands échantillons) Si n 1 & n 2 > 20, la distribution U peut être approchée par une distribution normale de telle sorte que avec Ceci se teste tout naturellement sur la loi normale… Accepter H 0 si –Za/2<Z<Za/2, sinon rejeter H 0 11/2/2020 Statistiques 71

2. Les tests – Le test de Wilcoxon Comparaison de deux échantillons appariés (chaque valeur d’un échantillon est associée à une valeur de l’autre échantillon, les deux ont la même taille). Question: Existe-t-il une différence entre les 2 échantillons? H 0: Pas de différence entre les deux groupes H 1: Une différence entre les deux groupes M 5 4 2 3 4 3 8 5 4 5 R 6 3 3 1 1 3 4 2 5 7 -1 2 3 0 4 3 -1 -2 Diff -1 1 Calcul de la différence n = nombre de différences non nulles = 9 11/2/2020 Statistiques 72

2. Les tests – Le test de Wilcoxon (petits échantillons) Test de Wilcoxon On classe ensuite les différences par ordre croissant de valeurs absolues Val. -1 Rg 1 -1 -1 2 -2 3 3 4 2. 5 5. 5 7. 5 9 On affecte à chaque différence son rang dans le classement w+ : somme des rangs des différences positives w- : somme des rangs des différences négatives w+ = 2. 5 + 5. 5 + 7. 5 + 9 = 32 w- = 2. 5 + 5. 5 = 13 w = min (w+, w-) = 13 11/2/2020 Statistiques 73

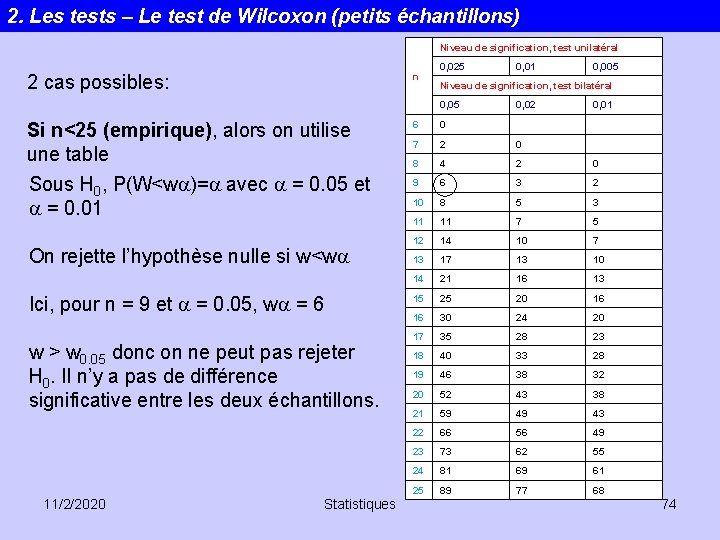
2. Les tests – Le test de Wilcoxon (petits échantillons) Niveau de signification, test unilatéral n 2 cas possibles: 0, 025 Sous H 0, P(W<wa)=a avec a = 0. 05 et a = 0. 01 On rejette l’hypothèse nulle si w<wa Ici, pour n = 9 et a = 0. 05, wa = 6 w > w 0. 05 donc on ne peut pas rejeter H 0. Il n’y a pas de différence significative entre les deux échantillons. 11/2/2020 Statistiques 0, 005 Niveau de signification, test bilatéral 0, 05 Si n<25 (empirique), alors on utilise une table 0, 01 0, 02 0, 01 6 0 7 2 0 8 4 2 0 9 6 3 2 10 8 5 3 11 11 7 5 12 14 10 7 13 10 14 21 16 13 15 25 20 16 16 30 24 20 17 35 28 23 18 40 33 28 19 46 38 32 20 52 43 38 21 59 49 43 22 66 56 49 23 73 62 55 24 81 69 61 25 89 77 68 74

2. Les tests – Le test de Wilcoxon (grands échantillons) Si n>25, lorsque H 0 est vraie, W suit approximativement une loi normale N(m, s) avec On calcule la valeur de la variable normale centrée réduite: La valeur est comparée à la valeur Za de la loi normale. Si –Za/2<Z<Za/2 on accepte H 0 11/2/2020 Statistiques 75

2. Les tests – Le test de Kolmogorov Smirnov Test non paramétrique de conformité de Kolmogorov Smirnov Il consiste à calculer les différences existants entre les distributions de fréquences relatives cumulées de deux échantillons et à vérifier si la plus grande différence peut être fortuite ou pas (Dobs). Pour au moins une valeur de xi Simple sur un exemple… 11/2/2020 Statistiques 76

2. Les tests – Le test de Kolmogorov Smirnov Domaine vital de l’ours noir (F & M) Sexe Domaine vital (km 2) Question: L’étendue du domaine vital des ours noirs males est-elle différente de celle du domaine des femelles? F F M M F F F 37 72 94 504 60 173 49 18 560 50 274 168 102 49 20 Hypothèses: Pour au moins une valeur de xi 11/2/2020 Statistiques 77

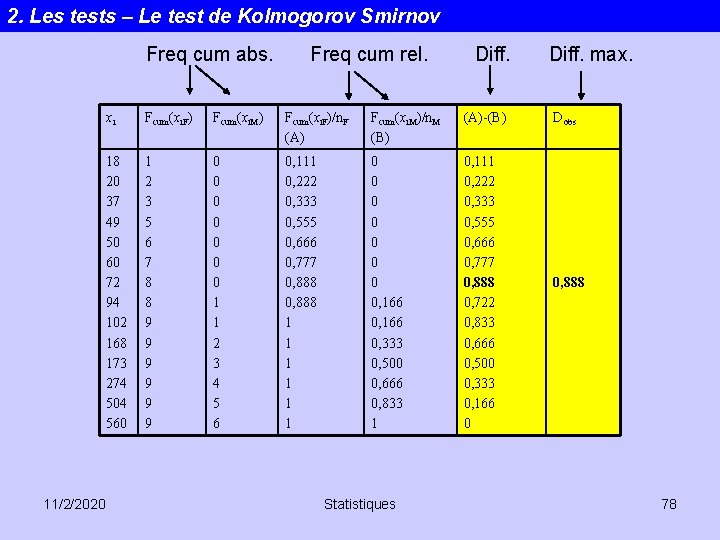
2. Les tests – Le test de Kolmogorov Smirnov Freq cum abs. 11/2/2020 Freq cum rel. Diff. xi Fcum(xi. F) Fcum(xi. M) Fcum(xi. F)/n. F (A) Fcum(xi. M)/n. M (B) (A)-(B) 18 20 37 49 50 60 72 94 102 168 173 274 504 560 1 2 3 5 6 7 8 8 9 9 9 0 0 0 0 1 1 2 3 4 5 6 0, 111 0, 222 0, 333 0, 555 0, 666 0, 777 0, 888 1 1 1 0 0 0 0, 166 0, 333 0, 500 0, 666 0, 833 1 0, 111 0, 222 0, 333 0, 555 0, 666 0, 777 0, 888 0, 722 0, 833 0, 666 0, 500 0, 333 0, 166 0 Statistiques Diff. max. Dobs 0, 888 78

2. Les tests – Le test de Kolmogorov Smirnov 11/2/2020 Statistiques 79

2. Les tests – Le test de Kolmogorov Smirnov Ici cas des petits échantillons n. F & n. M < 25 (en fait n. F=9 et n. M=6) On calcule une variable auxiliaire KS = n. F n. M Dobs = 9. 6. 0, 888 = 47, 952 = 48 Dans la table, la valeur critique s’élève à 39 pour a = 0, 05 Si KS>KSa, alors on rejete H 0 (rejet des valeurs trop grandes) Ici 48>39, donc on rejette H 0 Conclusion: L’étendue du domaine vital des mâles diffère significativement de l’étendue du domaine des femelles. 11/2/2020 Statistiques 80

2. Les tests – Le test de Kolmogorov Smirnov Si au contraire n 1 & n 2 sont supérieurs à 25 on calcule : Si Dobs > Da, l’hypothèse H 0 est refusée au profit de H 1 11/2/2020 Statistiques 81