L 2 Deterministic Finite Automata Representations 5 components

What are FAs? Finite automata are finite collections of states with transition rules that

Representing FA Graph representation of FAs Nodes = states. Arcs indicate state-to-state transitions. Labels

DFA accepting strings that contain “ing” We can get the next input character in

Rules for deterministic finite automata Not i or g Not i or n empty

Components of automata theory Alphabets: sets of symbols Strings: lists of symbols from an

Sets of Strings • The set of strings over alphabet Σ is a set

Languages • A language is a subset of strings for some alphabet • L=Σ*

Elements in the formal definition of a DFAs 1. Q = finite set of

The Transition Function • δ(q, a) = the state that the DFA goes to

Using graph to answer “Is this string in the language of DFA? ” Is

Is string in language by graph Is string 101 in the language of the

Transition function table: δ(q, a) is the element in row q of column a

Extended Transition Function, delta-hat u 16

Example: use the definition of delta-hat to test the acceptance of string 101 by

Formal proof of language content 0 A* B* C A A C 1 B

Questions about Assignment 2: Transition table Exercise 2. 2. 10: Text p 54 ->A

Slides: 32

Download presentation

L 2 Deterministic Finite Automata Representations 5 components that define a DFA Testing acceptance of a strings by DFA Induction on the length of a string 1

What are FAs? Finite automata are finite collections of states with transition rules that take you from one state to another. FAs process strings of instructions that may or may not lead to an accepting state. 2

Representing FA Graph representation of FAs Nodes = states. Arcs indicate state-to-state transitions. Labels on arcs tell input that caused the transition. Arrow denotes “start” state Double circles denote accepting (final) states 3

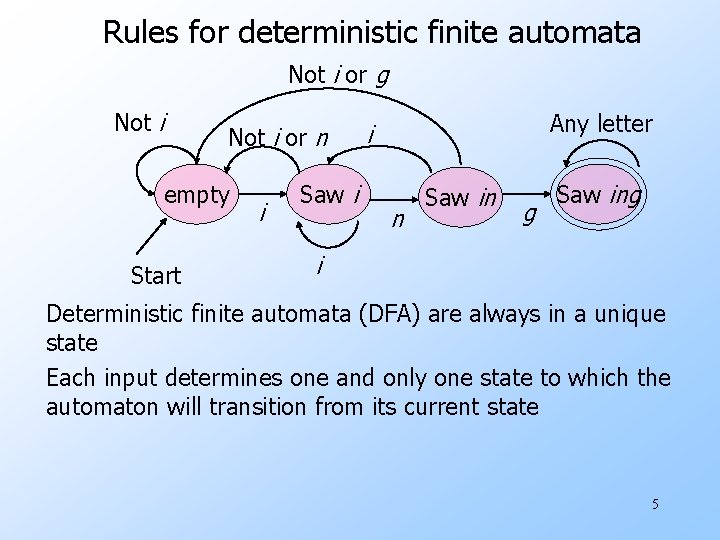
DFA accepting strings that contain “ing” We can get the next input character in any state Where we go depends on which character and which state Not i or g Not i or n empty Start i Saw i Any letter i n Saw in g Saw ing i String acceptance or rejection only determined after all input has been processed. 4

Rules for deterministic finite automata Not i or g Not i or n empty Start i Saw i Any letter i n Saw in g Saw ing i Deterministic finite automata (DFA) are always in a unique state Each input determines one and only one state to which the automaton will transition from its current state 5

Components of automata theory Alphabets: sets of symbols Strings: lists of symbols from an alphabet Languages: sets of strings from the same alphabet 6

Sets of Strings • The set of strings over alphabet Σ is a set of lists, each element of a list is a member of Σ • e denotes the empty string (length=0) • Σ* denotes the set of all strings over S including the empty string • Sk denotes strings of length k over a specified alphabet • S* = S 0 S 1 S 2 … • S 0={e} for any alphabet • S+ denotes non-empty strings • If x and y are strings, then xy is a string formed by 7 their concatenation

Languages • A language is a subset of strings for some alphabet • L=Σ* language of all strings from S • L can be empty • L={e} is not empty. Only contains the empty string • See text p 31 for examples from the binary alphabet {0, 1} 8

Elements in the formal definition of a DFAs 1. Q = finite set of states 2. Σ = input alphabet 3. δ = transition function 4. q 0 = start state in Q 5. F = set of final states ⊆ Q “Final” and “accepting” are synonyms. Set of strings accepted by DFA=(Q, S, d, q 0, F) is the language of the DFA 9

The Transition Function • δ(q, a) = the state that the DFA goes to when it is in state q and input a is processed. • In graph representation of a DFA, δ(q, a)=p is shown by arc from state q to state p labeled by a 10

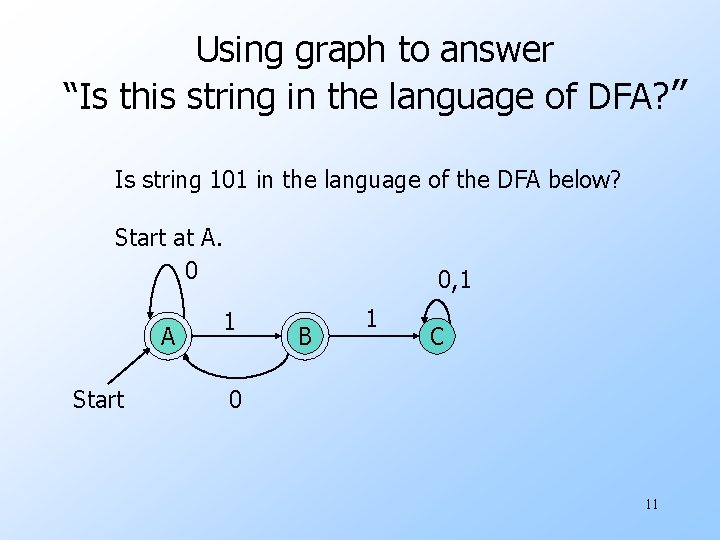
Using graph to answer “Is this string in the language of DFA? ” Is string 101 in the language of the DFA below? Start at A. 0 A Start 0, 1 1 B 1 C 0 11

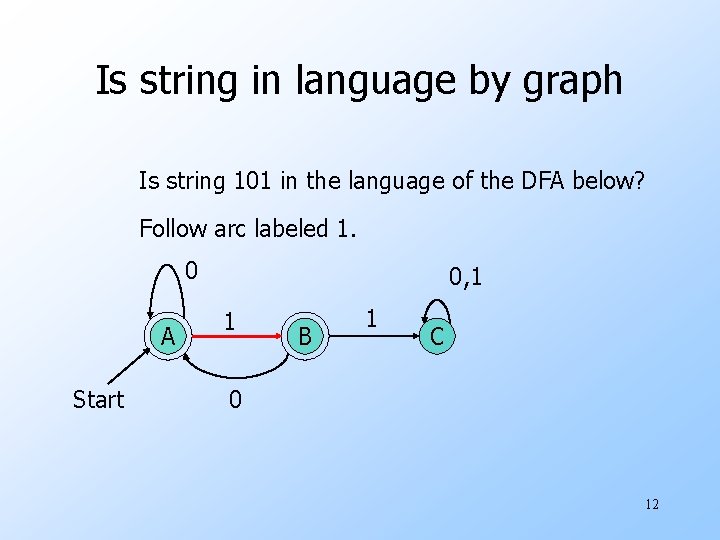
Is string in language by graph Is string 101 in the language of the DFA below? Follow arc labeled 1. 0 A Start 0, 1 1 B 1 C 0 12

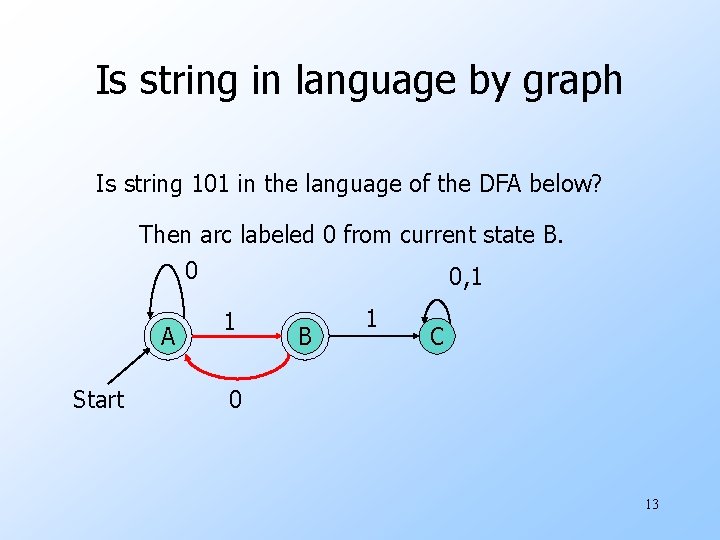
Is string in language by graph Is string 101 in the language of the DFA below? Then arc labeled 0 from current state B. 0 0, 1 A Start 1 B 1 C 0 13

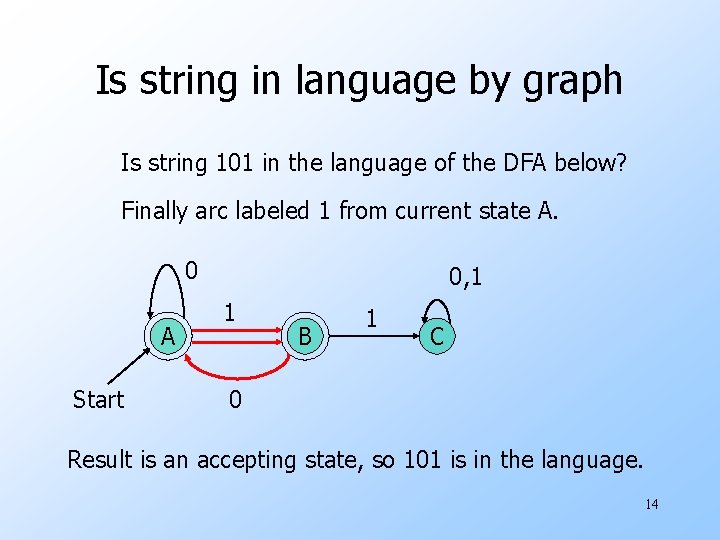
Is string in language by graph Is string 101 in the language of the DFA below? Finally arc labeled 1 from current state A. 0 A Start 0, 1 1 B 1 C 0 Result is an accepting state, so 101 is in the language. 14

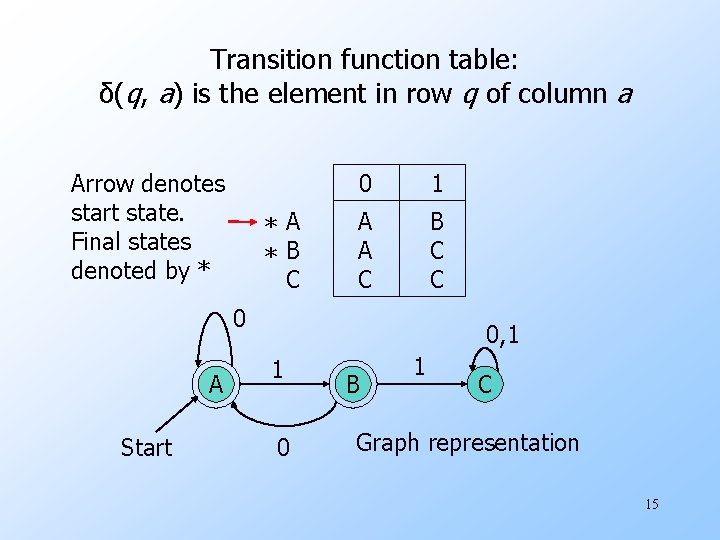
Transition function table: δ(q, a) is the element in row q of column a Arrow denotes start state. Final states denoted by * *A *B C 0 1 A A C B C C 0 A Start 0, 1 1 0 B 1 C Graph representation 15

Extended Transition Function, delta-hat u 16

Recursive definition of delta-hat u 17

Example: use the definition of delta-hat to test the acceptance of string 101 by the DFA defined by the transition function table A* B* C 0 A A C 1 B C C 18

A* B* C 0 A A C 1 B C C 19

Formal proof of language content 0 A* B* C A A C 1 B C C • Delta-hat and transition table make it easy to test if a particular string is in L(DFA) • Formal proof of language content is a problem in equality of sets that involves “induction on length of string” 20

Questions about Assignment 2: Transition table Exercise 2. 2. 10: Text p 54 ->A *B 0 A B 1 B A Draw the graph representation of this DFA Use “parity” to describe L(DFA) in words. L(DFA) is strings of 0 s and 1 s with an odd number of 1 s.