L 12 Chapter 4 Circuit Theorems From Chapter



















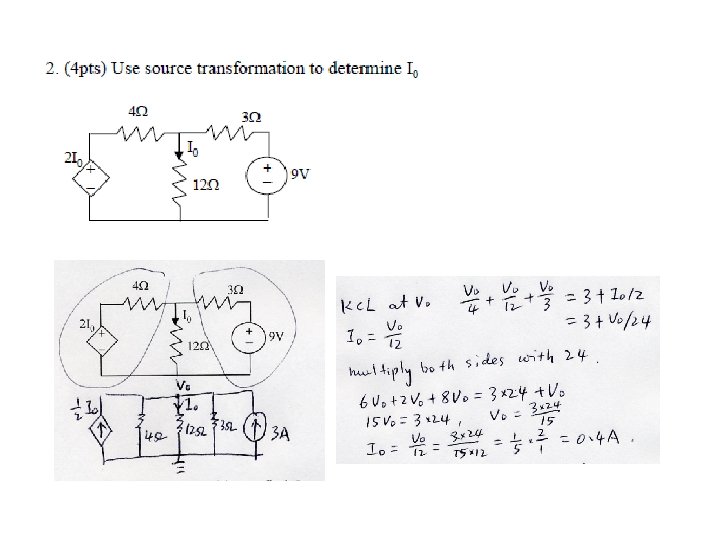

- Slides: 35

L 12 Chapter 4 Circuit Theorems From Chapter 2: Basic laws -- Foundations. From Chapter 3: Mesh analysis, Nodal analysis. Systematic tools, can be used for complex circuits. More useful tools to be learned in Chapter 4: 1. Linearity 2. Superposition 3. Source transformation 4. Thevenin’s Theorem 5. Norton’s Theorem 6. Maximum power transfer Could be more tricky than Chapters 2, 3. • There may exist several solutions to one problem • Need to develop insight to plan solutions ahead and identify the simplest solution

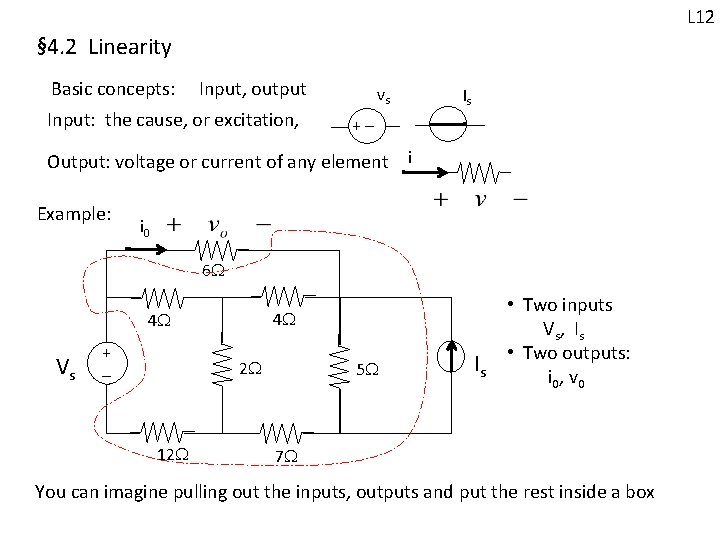
L 12 § 4. 2 Linearity Basic concepts: Input, output Input: the cause, or excitation, vs + - Output: voltage or current of any element Example: Is i i 0 6 4 4 Vs + - 2 12 5 Is • Two inputs Vs, Is • Two outputs: i 0, v 0 7 You can imagine pulling out the inputs, outputs and put the rest inside a box

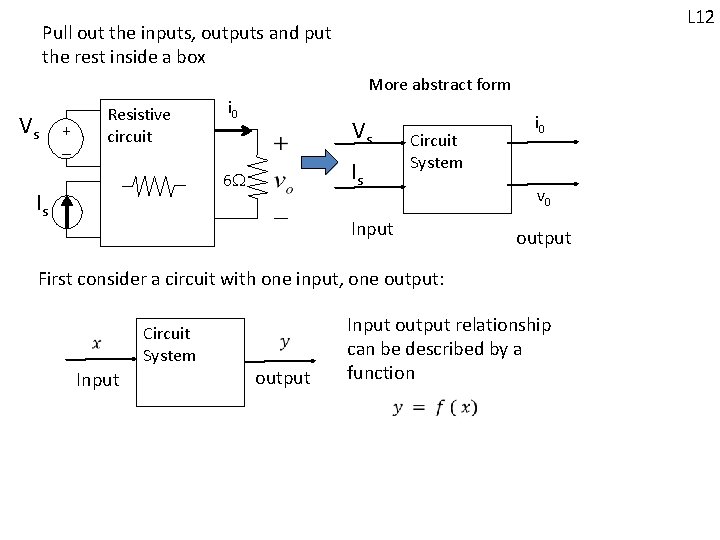
L 12 Pull out the inputs, outputs and put the rest inside a box More abstract form Vs Resistive circuit + - i 0 Vs Is 6 Is Circuit System i 0 v 0 Input output First consider a circuit with one input, one output: Input Circuit System output Input output relationship can be described by a function

L 12 Circuit System output Input Linearity: Two implications: Homogeneity: Additivity: Linearity = homogeneity + additivity If x 1 y 1, x 2 y 2, then ax 1 a y 1 then x 1+ x 2 y 1+ y 2

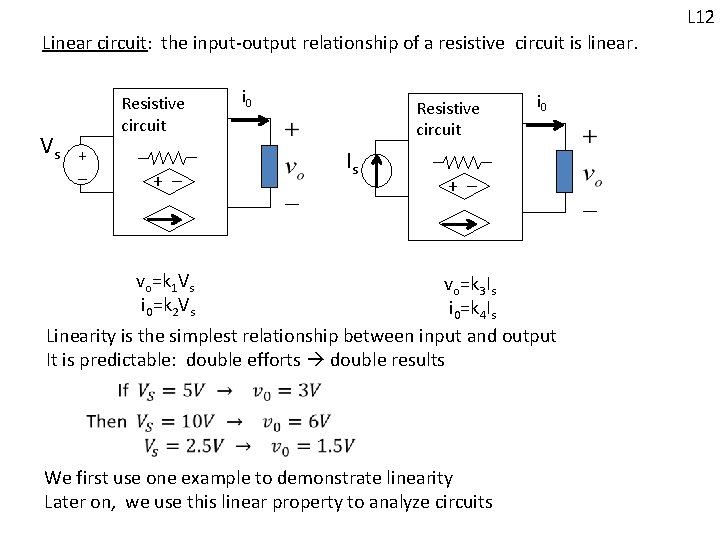
L 12 Linear circuit the input-output relationship of a resistive circuit is linear. : Vs Resistive circuit + - vo=k 1 Vs i 0=k 2 Vs i 0 Resistive circuit Is i 0 + - vo=k 3 Is i 0=k 4 Is Linearity is the simplest relationship between input and output It is predictable: double efforts double results We first use one example to demonstrate linearity Later on, we use this linear property to analyze circuits

L 12 Example: 2 8 4 i 1 Vs + - I 0 i 2 + - 6 4 Assign mesh currents i 1, i 2. 3 vx= 6 i 1 vx=2 i 1 I 0= i 2 KVL along mesh 1: KVL along mesh 2: Input: Vs Output: I 0 2 i 1+4(i 1 -i 2)+Vs+6 i 1=0 12 i 1 -4 i 2= -Vs (1) 8 i 2 - 3 vx+4 i 2 -Vs+4(i 2 -i 1) = 0 8 i 2 - 6 i 1 +4 i 2 -Vs+4(i 2 -i 1) = 0 -10 i 1+16 i 2 = Vs (2)

For this circuit, the input output relationship is derived by solving the output from the input The direct approach Given input find output, For some circuit, it is more convenient to find the input from the output. Given output find input, The backward approach In general, Input Linear Circuit output L 12

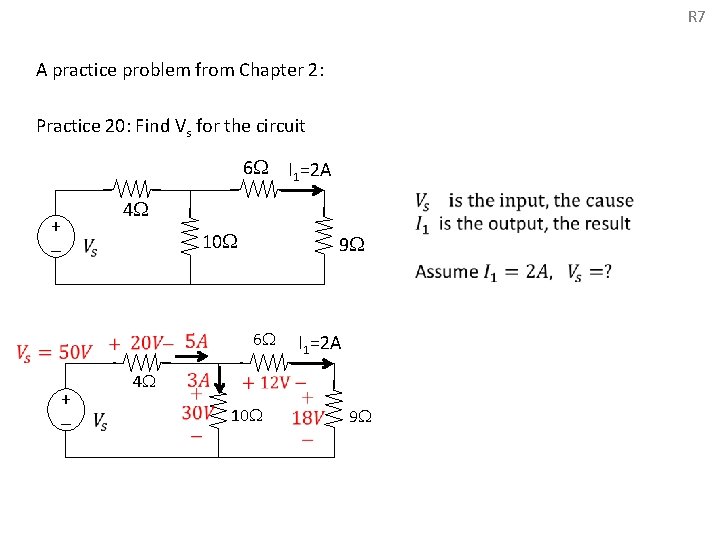
R 7 A practice problem from Chapter 2: Practice 20: Find Vs for the circuit 6 I 1=2 A + - 4 10 + - 9 4 6 I 1=2 A 10 9

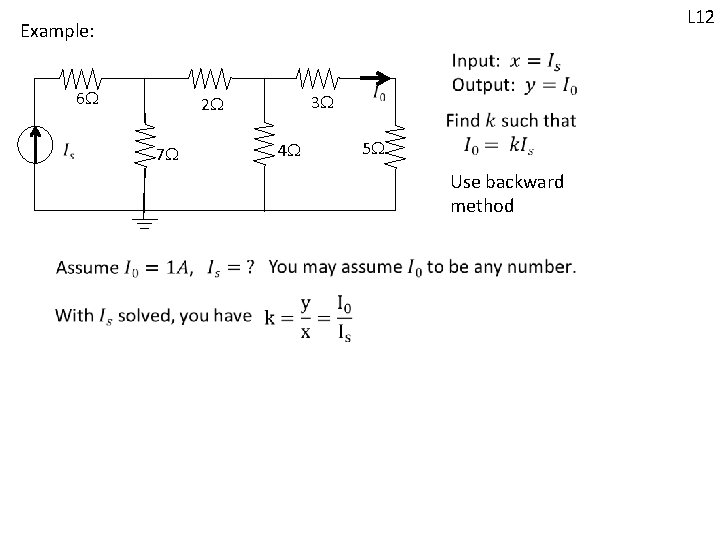
L 12 Example: 6 3 2 4 7 5 Use backward method

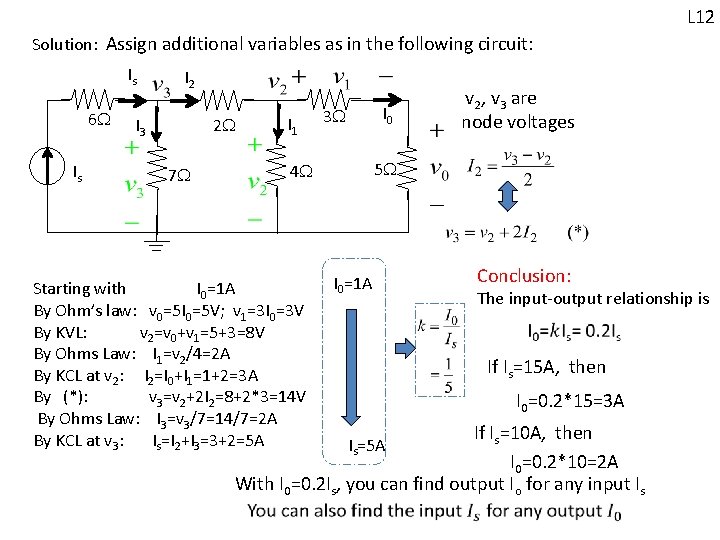
L 12 Solution: Assign additional variables as in the following circuit: Is 6 Is I 2 I 3 I 1 2 I 0 3 Starting with I 0=1 A By Ohm’s law: v 0=5 I 0=5 V; v 1=3 I 0=3 V By KVL: v 2=v 0+v 1=5+3=8 V By Ohms Law: I 1=v 2/4=2 A By KCL at v 2: I 2=I 0+I 1=1+2=3 A By (*): v 3=v 2+2 I 2=8+2*3=14 V By Ohms Law: I 3=v 3/7=14/7=2 A By KCL at v 3: Is=I 2+I 3=3+2=5 A node voltages 5 4 7 v 2, v 3 are I 0=1 A Conclusion: The input-output relationship is If Is=15 A, then I 0=0. 2*15=3 A If Is=10 A, then I 0=0. 2*10=2 A With I 0=0. 2 Is, you can find output Io for any input Is Is=5 A

L 12 A simple demonstration: 6 Is 3 2 7 4 5 6 Vs 7 2 3 4 5

L 12 § 4. 3 Superposition -- About the relationship between one output and several inputs the voltage across (or current through) an element in a Superposition principle: linear circuit, is the sum of voltage/current due to each independent source alone. Vs + i 0 Is v 0= v 1+v 2 i 0= i 1+ i 2 + - Is i 2 i 1 + - Vs + -

Key points: when you examine the effect due to one source, turn off the other sources • Turn off voltage source with short circuit • Turn of current source with open circuit L 12

Example : Find the output v. Step 1: Due to 6 V alone – turn off 3 A with open circuit 8Ω + - 6 V L 12 8Ω 4Ω 3 A v = v 1+v 2 = 2+8=10 V + - 6 V 4Ω By voltage division: Step 2: Due to 3 A – turn off 6 V with short circuit By equivalent resistance and ohm’s law 8Ω 4Ω 3 A Superposition breaks down a circuit into several circuits with only one independent source – typically can be solved with simple methods in Chapter 2.

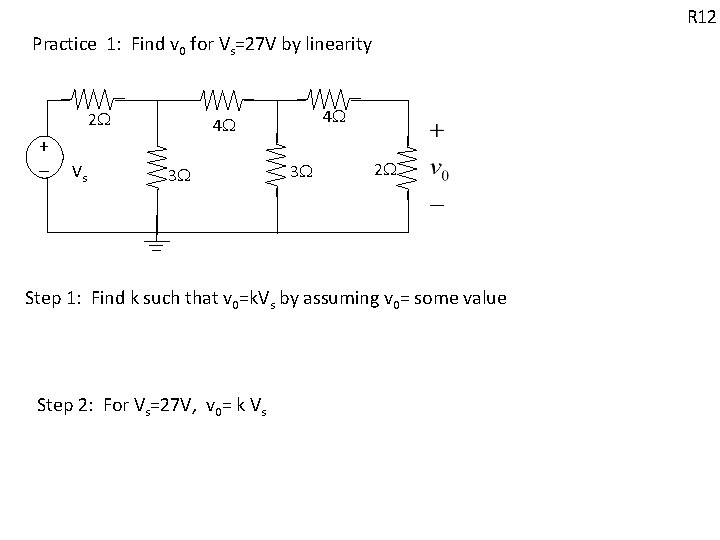
R 12 Practice 1: Find v 0 for Vs=27 V by linearity 2 + - Vs 4 4 3 3 2 Step 1: Find k such that v 0=k. Vs by assuming v 0= some value Step 2: For Vs=27 V, v 0= k Vs

R 12 Practice 2: Find i using linearity 8Ω 4Ω 4Ω i 3Ω 3 A

Practice 3: Find i using superposition. + - 24 V 4Ω + - 12 V 8Ω 4Ω i 3Ω 3 A R 12

Practice 4: Find i using superposition. + - 1Ω 6 A 24 V i 4Ω 3Ω 4Ω R 12

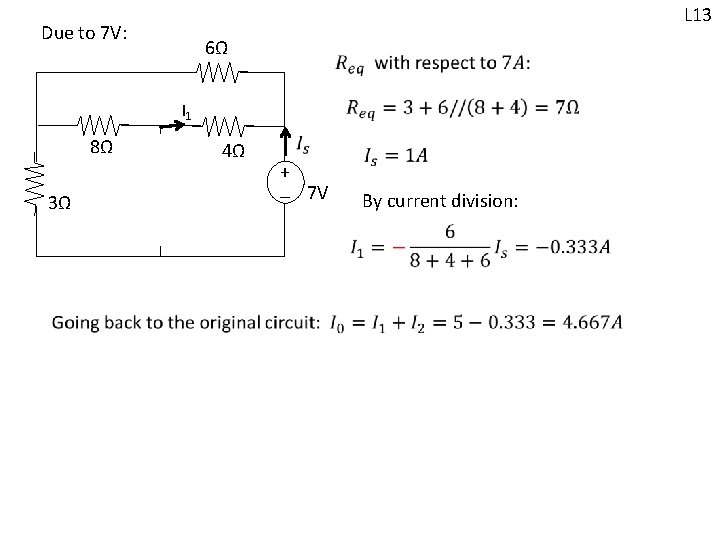
Example: Find I 0 using superposition. 6Ω I 0 4Ω 7 A Due to 7 A: 6Ω 8Ω + - 7 V 3Ω 8Ω 4Ω 7 A 4Ω + - 7 V Due to 7 V: replace 7 A with open circuit Due to 7 A: replace 7 V with short circuit I 2 3Ω 6Ω I 1 8Ω 3Ω L 13 Due to 7 V:

Due to 7 A: 6Ω I 2 4Ω 3Ω 3Ω 8Ω I 2 4Ω 7 A 6Ω 10Ω 3Ω I 2 7 A 4Ω 7 A 7 A 8Ω 3Ω I 2 8Ω 8Ω L 13 6Ω 4Ω 6Ω 7 A 4Ω

L 13 Due to 7 V: 6Ω I 1 8Ω 3Ω 4Ω + - 7 V By current division:

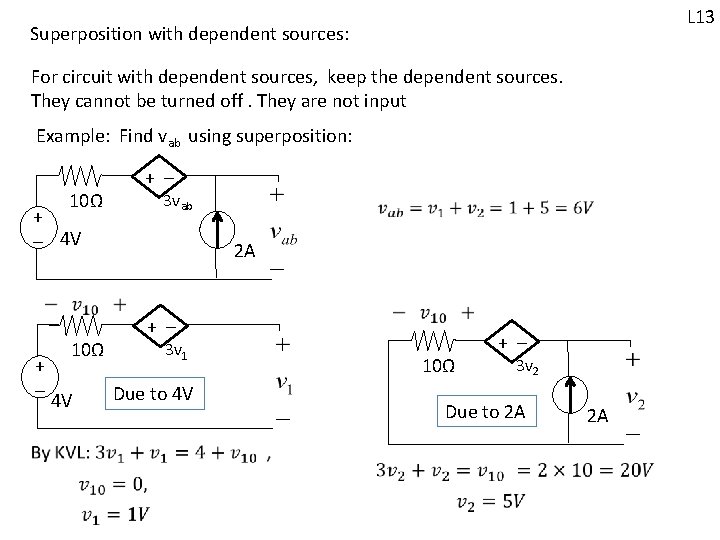
L 13 Superposition with dependent sources: For circuit with dependent sources, keep the dependent sources. They cannot be turned off. They are not input Example: Find vab using superposition: 10Ω + - 4 V + - 3 vab 2 A + - 10Ω + - 3 v 1 10Ω Due to 4 V 4 V + - 3 v 2 Due to 2 A

L 13 § 4. 4: Source transformation A general situation: you can separate a circuit as the connection of two parts. i Circuit A Circuit C You may need to make change to one part, But want to ensure this change does not affect the other part For circuit A, you can obtain a function v = f (i) If there is another circuit B, with the same v i relationship, You can replace Circuit A with Circuit B without affecting Circuit C i Circuit B Circuit C All variables in Circuit C are unchanged, But the variables in Circuit A may not exist in Circuit B. Sometimes you need to replace a complex circuit with a simpler one; as with Thevenin’s equivalent Sometimes with one which is more convenient for analysis as with source transformation

L 13 Compare the two connections: Circuit B: Circuit A: i + - R 1 i s i R vs By KVL, v = vs-v. R= vs-R 1 i v = vs-R 1 i To have the same v i relationship: By KCL, i. R= is-I v = R 2 i. R= R 2 is- R 2 i v = R 2 is- R 2 i R 1=R 2, Vs=R 2 is i R 2

L 13 Conclusion: The following two connections are equivalent i i + - R vs vs= Ris i R R If you replace one with another, the rest of the circuit will not be affected. However, be careful: The voltages across resistor R in the two circuits are different; The currents through R in the two circuits also different.

L 13 Extension to dependent sources: The following two connections are equivalent i i + - R vs= Ris i s v s R For example, if is= kvx, then vs=Ris=Rkvx If vs= ki 0, then is=ki 0/R The rule: if you put the two sources side by side, the arrow of the current source points from – to + of the voltage source

L 13 i i vs= Ris i s R v s + - R v s R i All equivalent i i s R

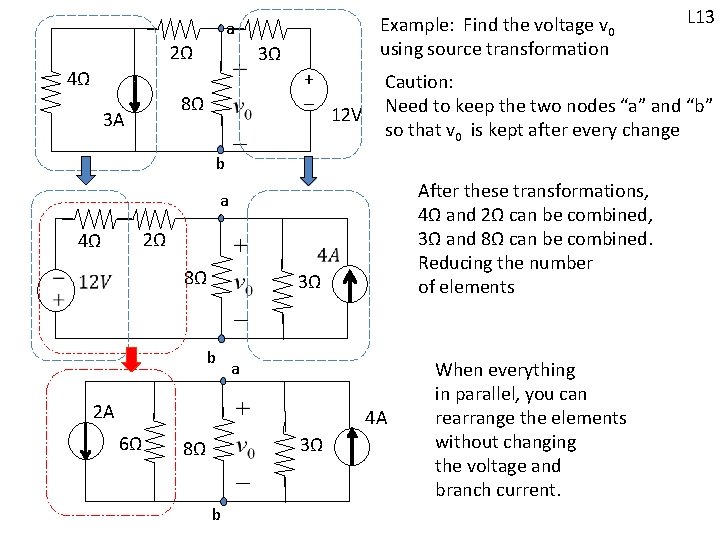
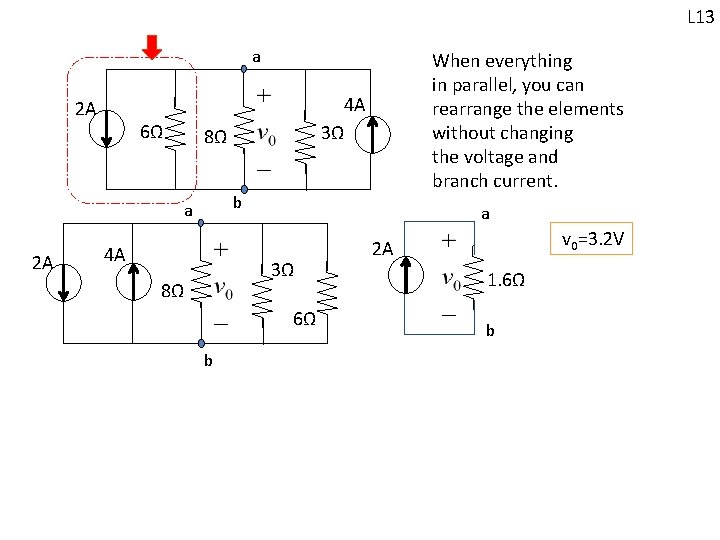
Example: Find the voltage v 0 using source transformation a 2Ω 3Ω 4Ω + - 8Ω 3 A 12 V Caution: Need to keep the two nodes “a” and “b” so that v 0 is kept after every change b After these transformations, 4Ω and 2Ω can be combined, 3Ω and 8Ω can be combined. Reducing the number of elements a 2Ω 4Ω 8Ω 3Ω b a 2 A 4 A 6Ω 3Ω 8Ω b L 13 When everything in parallel, you can rearrange the elements without changing the voltage and branch current.

L 13 a 2 A 6Ω 4 A 3Ω 8Ω b a 2 A When everything in parallel, you can rearrange the elements without changing the voltage and branch current. 4 A a 3Ω 8Ω 6Ω b v 0=3. 2 V 2 A 1. 6Ω b

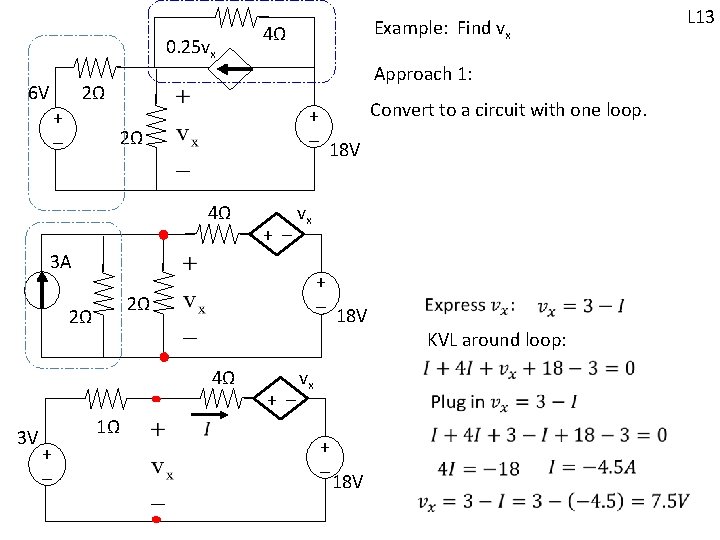
0. 25 vx 6 V 4Ω Approach 1: 2Ω + - Convert to a circuit with one loop. + - 18 V 2Ω 4Ω + - vx 3 A + - 18 V 2Ω 2Ω 4Ω 3 V 1Ω + - L 13 Example: Find vx + - KVL around loop: vx + - 18 V

0. 25 vx 6 V 4Ω 2Ω + - 18 V 2Ω 4Ω + - 3 A 2Ω Approach 2: Convert to a circuit with two nodes. Combine parallel resistors 4Ω//2Ω=0. 8Ω Combine parallel current sources vx + - 18 V 2Ω 0. 8Ω 3 A 2Ω 2Ω 4Ω vx=7. 5 V L 13


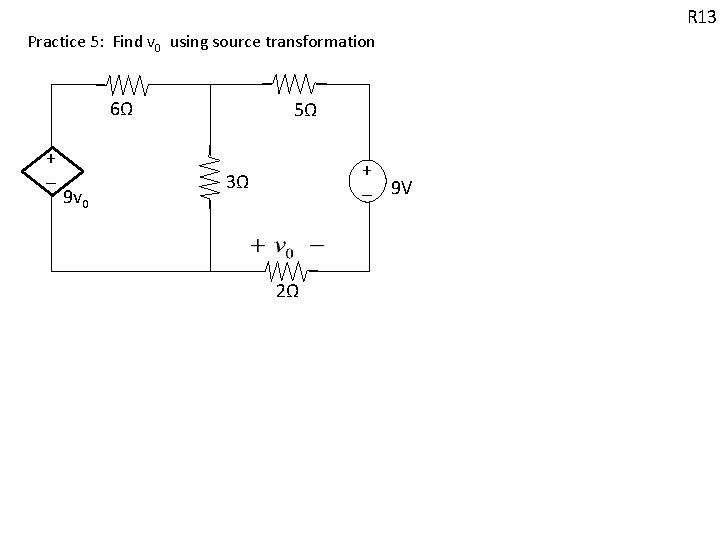
R 13 Practice 5: Find v 0 using source transformation 6Ω + - 9 v 0 5Ω + - 9 V 3Ω 2Ω

R 13 Practice 6: Find v 0 using source transformation 3 A 2Ω 2Ω 2Ω 10 V + - 2 A 3Ω 4 A

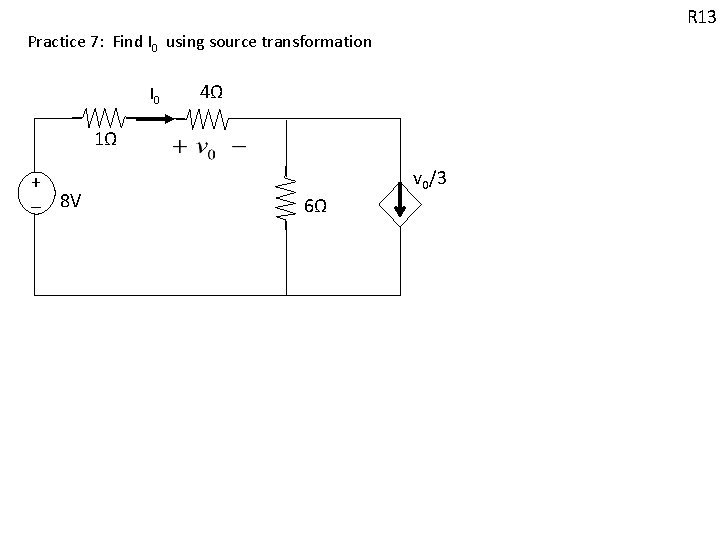
R 13 Practice 7: Find I 0 using source transformation I 0 4Ω 1Ω + - 8 V v 0/3 6Ω