Kvantitatv mdszerek LER STATISZTIKA 2013 oktber 8 2013

Kvantitatív módszerek LEÍRÓ STATISZTIKA 2013. október 8. 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

Statisztikai módszertan ágai n n LEÍRÓ vagy DESKRIPTÍV statisztika o A vizsgálat tárgyát képező jelenség tömör, számszerű jellemzését adja. o Nem lép túl a megfigyelés körén, de a megfigyelt adatok legjobb megértésére, bemutatására, összefoglaló jellemzésére törekszik. Például: o Népszámlálási adatok feldolgozása, elemzése, a népesség számával, összetételével kapcsolatos jellemzők közzététele, megjelenítése o Gazdasági szervezetek legfontosabb adatainak közzététele statisztikai évkönyvekben o Lakásépítésről, oktatásról készített statisztikai összefoglaló o Vállalat gazdálkodásának vizsgálata 2013 ősz Gazdaságstatisztika Kvantitatív módszerek 2

Statisztikai módszertan ágai n n KÖVETKEZTETŐ statisztika o Fő célja a mintából való következtetés, általánosítás a teljes sokaságra vonatkozóan. Például: o Minőség-ellenőrzés o Lakosság jövedelmi különbségeinek elemzése o Ingatlan árbecslések o Befektetési tanácsadások o Könyvvizsgálat o Mezőgazdaság 2013 ősz Gazdaságstatisztika Kvantitatív módszerek 3

Leíró statisztika n Területei: 1. 2. 3. 4. 5. adatgyűjtés adatok ábrázolása adatok csoportosítása, osztályozása adatokkal végzett egyszerűbb aritmetikai műveletek eredmények megjelenítése 4 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

1. Adatgyűjtés n n Az egyedi mérésekből származó adatok (mennyiségi ismérvek) lehetnek diszkrétek és folytonosak. Egy diszkrét mennyiségi ismérv csak véges vagy megszámlálhatóan sok, egymástól jól elkülöníthető értéket vehet fel. o o o n Háztartások nagysága Gazdálkodó szervezetek nagysága Balesetek száma Mogyorós csokiban a mogyorók száma Adott időszak alatti meghibásodások száma Egy folytonos mennyiségi ismérv valamely adott intervallumon belül bármilyen értéket felvehet. o o Háztartások jövedelme Lakások alapterülete Gépkocsi abroncsok futásteljesítménye Bux index havi hozamadata 2013 ősz Gazdaságstatisztika Kvantitatív módszerek 5

2. Az adatok ábrázolása n Eszközei: o Oszlopdiagram o Kördiagram o Vonaldiagram o Sávdiagram 6 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

3. Adatok csoportosítása, osztályozása n n n Egy mennyiségi ismérv szerinti rendezés és osztályozás o X mennyiségi ismérv (Xi változatai különbségi vagy arányskálán mért, valamilyen mértékegységgel rendelkező számértékek) o X a továbbiakban változó, Xi (ismérv)érték Rangsor o A sokaság egységeinek sorba rendezése az X változó nagysága szerint o A rangsor a megfigyelési egységeknek és/vagy azokhoz tartozó Xi ismérvértékeknek monoton nemcsökkenő sorrendben történő felsorolása. o Készítésének célja: megkönnyítse a sokaság egységeinek X változó szerinti osztályozását Osztályozás o Gyakorisági sor, gyakorisági eloszlás 7 2013 ősz Gazdaságstatisztika Kvantitatív módszerek
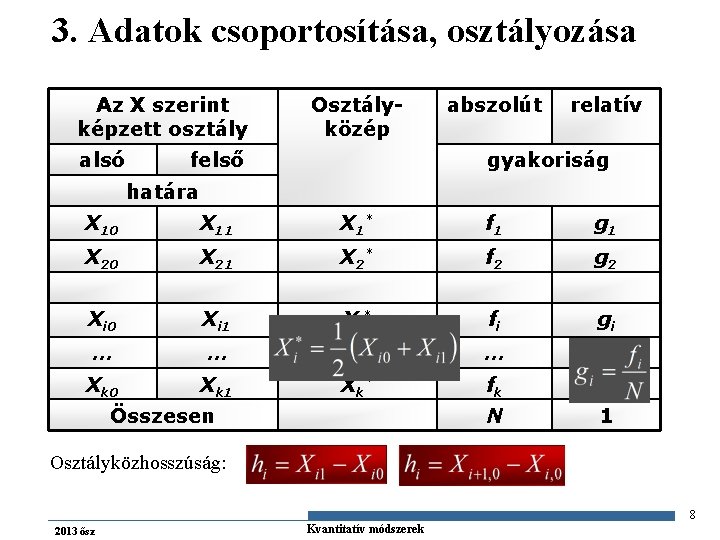
3. Adatok csoportosítása, osztályozása Az X szerint képzett osztály alsó Osztályközép felső abszolút relatív gyakoriság határa X 10 X 11 X 1* f 1 g 1 X 20 X 21 X 2* f 2 g 2 Xi 0 Xi 1 Xi* fi gi … … … Xk 0 Xk 1 Xk * fk gk N 1 Összesen Osztályközhosszúság: 8 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

3. Adatok csoportosítása, osztályozása n X ismérv szerinti osztályozás kérdései: o o n Az X változó diszkrét, és az általa felvehető értékek száma kicsi n Annyi osztályt képezünk ahány különböző X érték lehetséges n az i-edik osztály esetében fennáll az alsó és felső osztályhatár egybeesése Az X változó folytonos, vagy diszkrét ugyan, de az általa felvehető különböző értékek száma nagy n X lehetséges értékeinek tartományát osztályközökre bontjuk n az i-edik osztályköz Xi 1 felső határa nem eshet egybe az (i+1)-dik osztályköz Xi+1, 0 alsó határával Hány osztályt képezzünk? o o Egy osztályozás akkor megfelelő, ha az osztályok számának és határainak egy bizonyos sávon belüli változtatása nem nagyon befolyásolja a grafikus képet. A gyakorlatban ehhez 5 -15 osztály használata szinte mindig elegendő. Osztályok számának meghatározása: 9 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

3. Adatok csoportosítása, osztályozása n A mennyiségi sorok grafikus ábrázolásának alapját a gyakorisági táblázat készítése jelenti. 1. Osztályba sorolás (folytonos adatok és nagyszámú diszkrét megfigyelés esetén); 2. gyakoriságok (fi) megállapítása; 3. relatív gyakoriságok (gi) megállapítása 4. összegzett (kumulált) gyakoriságok (fi’), illetve összegzett relatív gyakoriságok (gi’) megállapítása; 5. gyakorisági táblázat készítése (fi , gi , fi’ , gi’ adataiból); 6. gyakorisági (relatív gyakorisági), illetve összegzett gyakorisági (relatív gyakorisági) hisztogramok (folytonos adatok esetén a poligon és az ogiva) felvétele (tapasztalati eloszlások elkészítése); 7. grafikus ábrázolás 2013 ősz Gazdaságstatisztika Kvantitatív módszerek 10
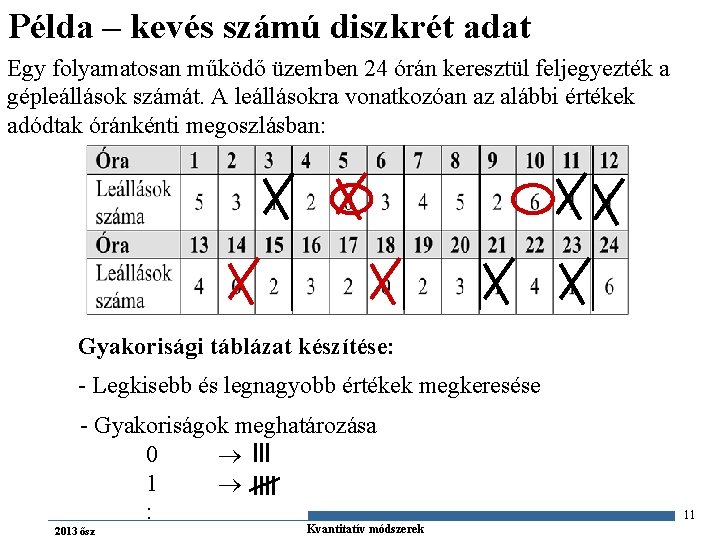
Példa – kevés számú diszkrét adat Egy folyamatosan működő üzemben 24 órán keresztül feljegyezték a gépleállások számát. A leállásokra vonatkozóan az alábbi értékek adódtak óránkénti megoszlásban: Gyakorisági táblázat készítése: - Legkisebb és legnagyobb értékek megkeresése - Gyakoriságok meghatározása 0 1 : 2013 ősz Gazdaságstatisztika Kvantitatív módszerek 11
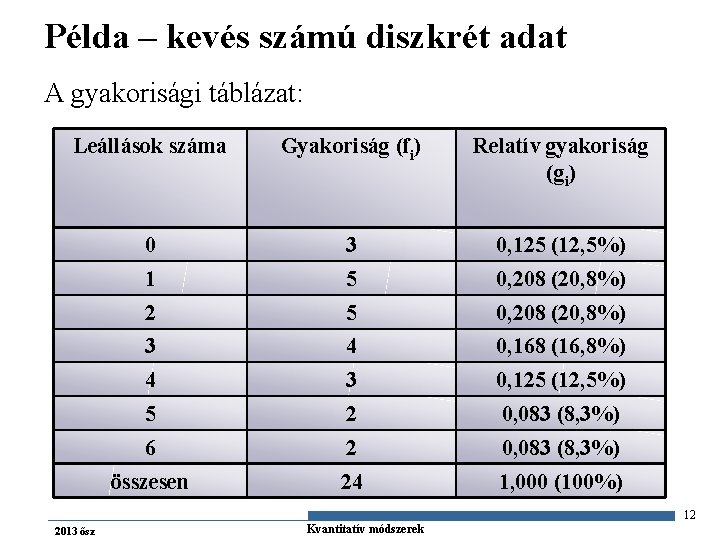
Példa – kevés számú diszkrét adat A gyakorisági táblázat: Leállások száma Gyakoriság (fi) Relatív gyakoriság (gi) 0 3 0, 125 (12, 5%) 1 5 0, 208 (20, 8%) 2 5 0, 208 (20, 8%) 3 4 0, 168 (16, 8%) 4 3 0, 125 (12, 5%) 5 2 0, 083 (8, 3%) 6 2 0, 083 (8, 3%) összesen 24 1, 000 (100%) 12 2013 ősz Gazdaságstatisztika Kvantitatív módszerek
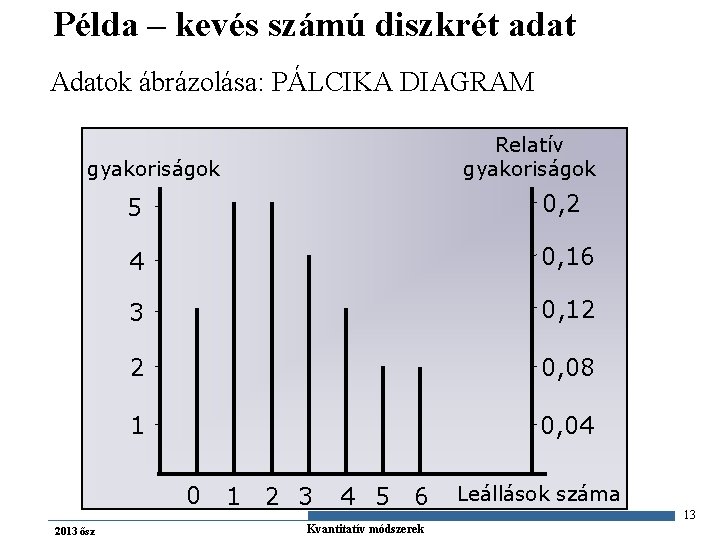
Példa – kevés számú diszkrét adat Adatok ábrázolása: PÁLCIKA DIAGRAM Relatív gyakoriságok 5 0, 2 4 0, 16 3 0, 12 2 0, 08 1 0, 04 2013 ősz 0 1 2 3 4 5 6 Gazdaságstatisztika Kvantitatív módszerek Leállások száma 13
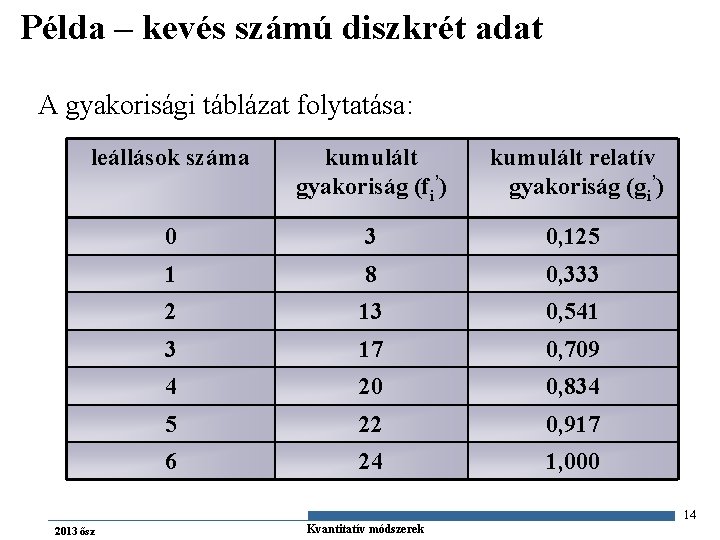
Példa – kevés számú diszkrét adat A gyakorisági táblázat folytatása: leállások száma kumulált gyakoriság (fi’) kumulált relatív gyakoriság (gi’) 0 3 0, 125 1 8 0, 333 2 13 0, 541 3 17 0, 709 4 20 0, 834 5 22 0, 917 6 24 1, 000 14 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

Példa – kevés számú diszkrét adat Kumulált relatív gyakoriságok Kumulált relatív gyakoriság ábrázolása: 1 0, 5 0 1 2 3 4 5 6 Leállások száma 15 2013 ősz Gazdaságstatisztika Kvantitatív módszerek
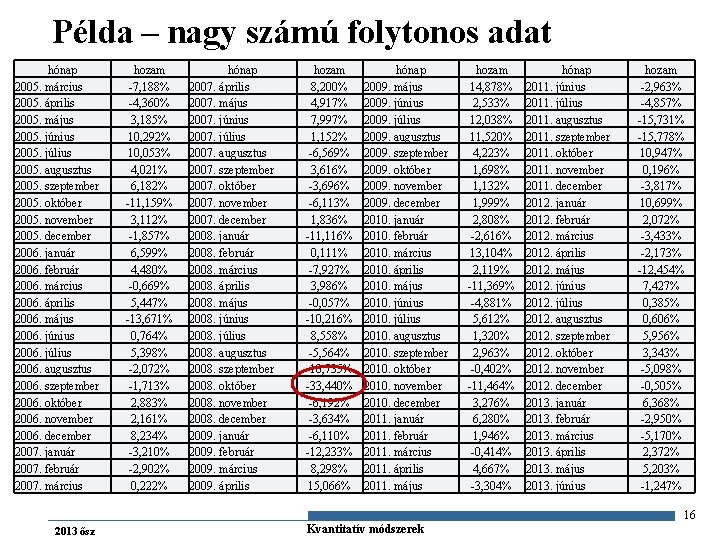
Példa – nagy számú folytonos adat hónap 2005. március 2005. április 2005. május 2005. június 2005. július 2005. augusztus 2005. szeptember 2005. október 2005. november 2005. december 2006. január 2006. február 2006. március 2006. április 2006. május 2006. június 2006. július 2006. augusztus 2006. szeptember 2006. október 2006. november 2006. december 2007. január 2007. február 2007. március hozam -7, 188% -4, 360% 3, 185% 10, 292% 10, 053% 4, 021% 6, 182% -11, 159% 3, 112% -1, 857% 6, 599% 4, 480% -0, 669% 5, 447% -13, 671% 0, 764% 5, 398% -2, 072% -1, 713% 2, 883% 2, 161% 8, 234% -3, 210% -2, 902% 0, 222% hónap 2007. április 2007. május 2007. június 2007. július 2007. augusztus 2007. szeptember 2007. október 2007. november 2007. december 2008. január 2008. február 2008. március 2008. április 2008. május 2008. június 2008. július 2008. augusztus 2008. szeptember 2008. október 2008. november 2008. december 2009. január 2009. február 2009. március 2009. április hozam 8, 200% 4, 917% 7, 997% 1, 152% -6, 569% 3, 616% -3, 696% -6, 113% 1, 836% -11, 116% 0, 111% -7, 927% 3, 986% -0, 057% -10, 216% 8, 558% -5, 564% -10, 735% -33, 440% -6, 192% -3, 634% -6, 110% -12, 233% 8, 298% 15, 066% hónap 2009. május 2009. június 2009. július 2009. augusztus 2009. szeptember 2009. október 2009. november 2009. december 2010. január 2010. február 2010. március 2010. április 2010. május 2010. június 2010. július 2010. augusztus 2010. szeptember 2010. október 2010. november 2010. december 2011. január 2011. február 2011. március 2011. április 2011. május hozam 14, 878% 2, 533% 12, 038% 11, 520% 4, 223% 1, 698% 1, 132% 1, 999% 2, 808% -2, 616% 13, 104% 2, 119% -11, 369% -4, 881% 5, 612% 1, 320% 2, 963% -0, 402% -11, 464% 3, 276% 6, 280% 1, 946% -0, 414% 4, 667% -3, 304% hónap 2011. június 2011. július 2011. augusztus 2011. szeptember 2011. október 2011. november 2011. december 2012. január 2012. február 2012. március 2012. április 2012. május 2012. június 2012. július 2012. augusztus 2012. szeptember 2012. október 2012. november 2012. december 2013. január 2013. február 2013. március 2013. április 2013. május 2013. június hozam -2, 963% -4, 857% -15, 731% -15, 778% 10, 947% 0, 196% -3, 817% 10, 699% 2, 072% -3, 433% -2, 173% -12, 454% 7, 427% 0, 385% 0, 606% 5, 956% 3, 343% -5, 098% -0, 505% 6, 368% -2, 950% -5, 170% 2, 372% 5, 203% -1, 247% 16 2013 ősz Gazdaságstatisztika Kvantitatív módszerek
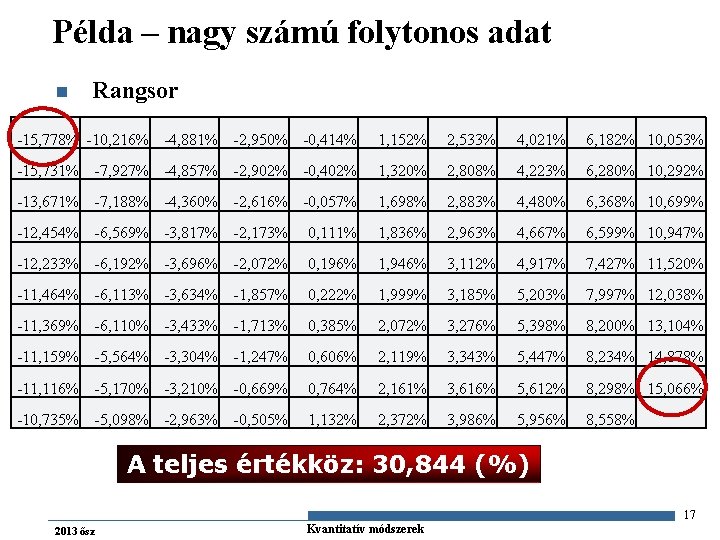
Példa – nagy számú folytonos adat n Rangsor -15, 778% -10, 216% -4, 881% -2, 950% -0, 414% 1, 152% 2, 533% 4, 021% 6, 182% 10, 053% -15, 731% -7, 927% -4, 857% -2, 902% -0, 402% 1, 320% 2, 808% 4, 223% 6, 280% 10, 292% -13, 671% -7, 188% -4, 360% -2, 616% -0, 057% 1, 698% 2, 883% 4, 480% 6, 368% 10, 699% -12, 454% -6, 569% -3, 817% -2, 173% 0, 111% 1, 836% 2, 963% 4, 667% 6, 599% 10, 947% -12, 233% -6, 192% -3, 696% -2, 072% 0, 196% 1, 946% 3, 112% 4, 917% 7, 427% 11, 520% -11, 464% -6, 113% -3, 634% -1, 857% 0, 222% 1, 999% 3, 185% 5, 203% 7, 997% 12, 038% -11, 369% -6, 110% -3, 433% -1, 713% 0, 385% 2, 072% 3, 276% 5, 398% 8, 200% 13, 104% -11, 159% -5, 564% -3, 304% -1, 247% 0, 606% 2, 119% 3, 343% 5, 447% 8, 234% 14, 878% -11, 116% -5, 170% -3, 210% -0, 669% 0, 764% 2, 161% 3, 616% 5, 612% 8, 298% 15, 066% -10, 735% -5, 098% -2, 963% -0, 505% 1, 132% 2, 372% 3, 986% 5, 956% 8, 558% A teljes értékköz: 30, 844 (%) 17 2013 ősz Gazdaságstatisztika Kvantitatív módszerek
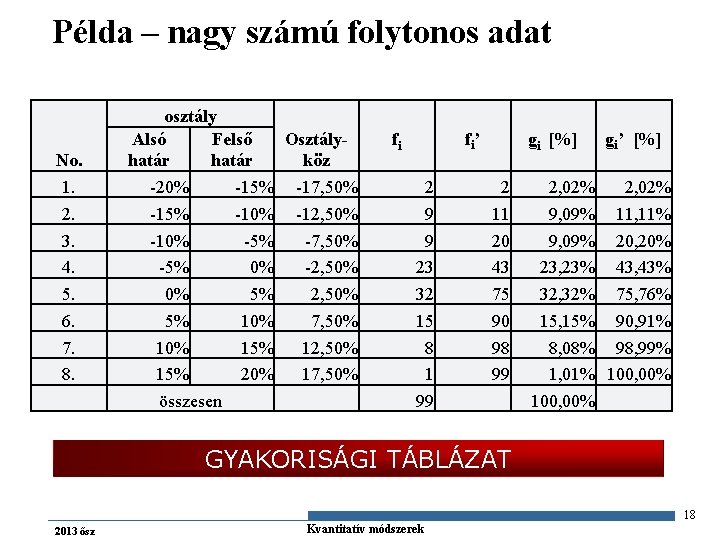
Példa – nagy számú folytonos adat No. 1. 2. 3. 4. 5. 6. 7. 8. osztály Alsó Felső Osztályhatár köz -20% -15% -17, 50% -15% -10% -12, 50% -10% -5% -7, 50% -5% 0% -2, 50% 0% 5% 2, 50% 5% 10% 7, 50% 15% 12, 50% 15% 20% 17, 50% összesen fi fi’ 2 9 9 23 32 15 8 1 99 gi [%] 2 11 20 43 75 90 98 99 2, 02% 9, 09% 23, 23% 32, 32% 15, 15% 8, 08% 1, 01% 100, 00% gi’ [%] 2, 02% 11, 11% 20, 20% 43, 43% 75, 76% 90, 91% 98, 99% 100, 00% GYAKORISÁGI TÁBLÁZAT 18 2013 ősz Gazdaságstatisztika Kvantitatív módszerek
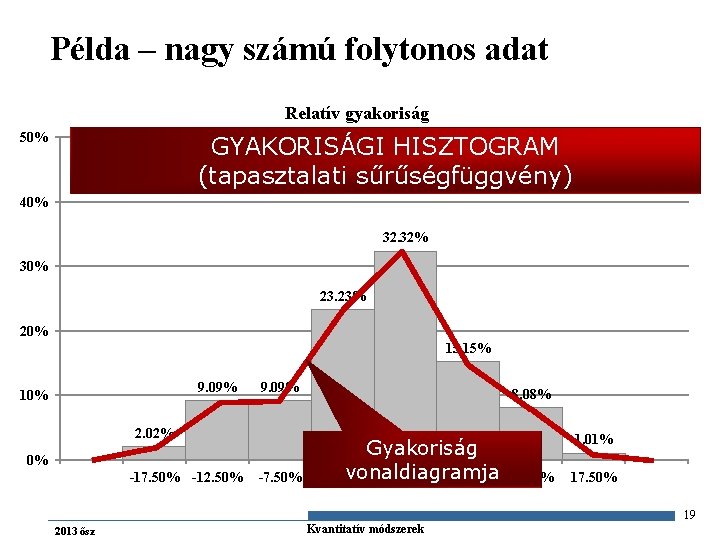
Példa – nagy számú folytonos adat Relatív gyakoriság 50% GYAKORISÁGI HISZTOGRAM (tapasztalati sűrűségfüggvény) 40% 32. 32% 30% 23. 23% 20% 15. 15% 9. 09% 10% 9. 09% 2. 02% 0% -17. 50% -12. 50% -7. 50% 8. 08% Gyakoriság vonaldiagramja -2. 50% 7. 50% 1. 01% 12. 50% 17. 50% 19 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

Példa – nagy számú folytonos adat Gyakorisági görbe 20 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

Példa – nagy számú folytonos adat 100% 90. 91% 98. 99% 100. 00% 90% Kumulált relatív gyakoriság 80% 75. 76% 70% 60% 50% 43. 43% 40% Kumulált relatív gyakoriság vonaldiagramja 30% 20. 20% 11. 11% 10% 2. 02% 0% -17. 50% -12. 50% -7. 50% -2. 50% 7. 50% 12. 50% 17. 50% Osztályközép 2013 ősz KUMULÁLT RELATÍV GYAKORISÁGI HISZTOGRAM Gazdaságstatisztika Kvantitatív módszerek 21
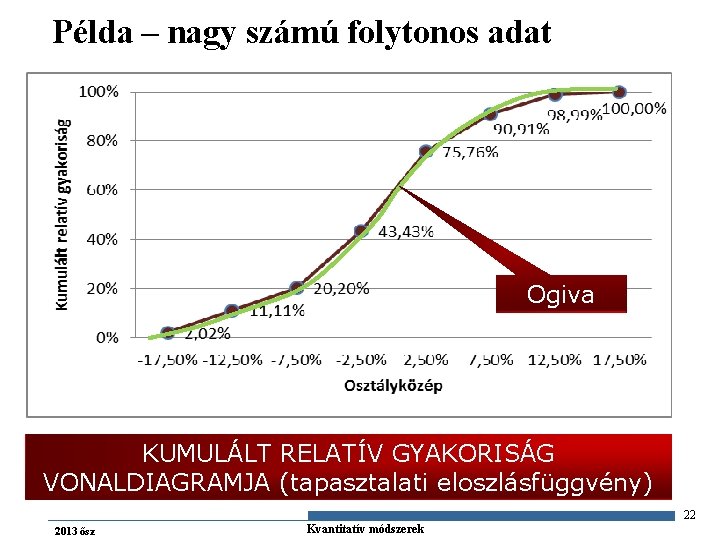
Példa – nagy számú folytonos adat Ogiva KUMULÁLT RELATÍV GYAKORISÁG VONALDIAGRAMJA (tapasztalati eloszlásfüggvény) 22 2013 ősz Gazdaságstatisztika Kvantitatív módszerek
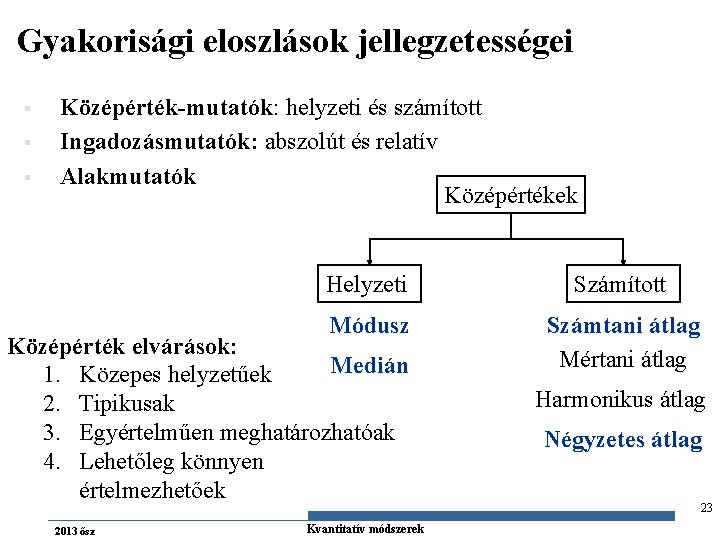
Gyakorisági eloszlások jellegzetességei § § § Középérték-mutatók: helyzeti és számított Ingadozásmutatók: abszolút és relatív Alakmutatók Középértékek Helyzeti Számított Módusz Számtani átlag Mértani átlag Középérték elvárások: Medián 1. Közepes helyzetűek 2. Tipikusak 3. Egyértelműen meghatározhatóak 4. Lehetőleg könnyen értelmezhetőek 2013 ősz Gazdaságstatisztika Kvantitatív módszerek Harmonikus átlag Négyzetes átlag 23

Medián n Helyzeti középérték – valódi középérték, a rangsor közepén található: az az érték, amelynél az előforduló értékek fele kisebb, fele pedig nagyobb o Páratlan számú adatnál a középső o Páros számú adatnál a két középső érték számtani átlaga n Mindig meghatározható n Érzéketlen a szélsőértékekre, és nem függ a többi ismérvértéktől sem n Sok egyforma ismérvérték esetén azonban nem tanácsos használni ha 11 00 66 1717 2323 1313 33 22 19 00 11 22 33 66 1313 1717 1923 23 4, 5 2013 ősz Gazdaságstatisztika Kvantitatív módszerek 24
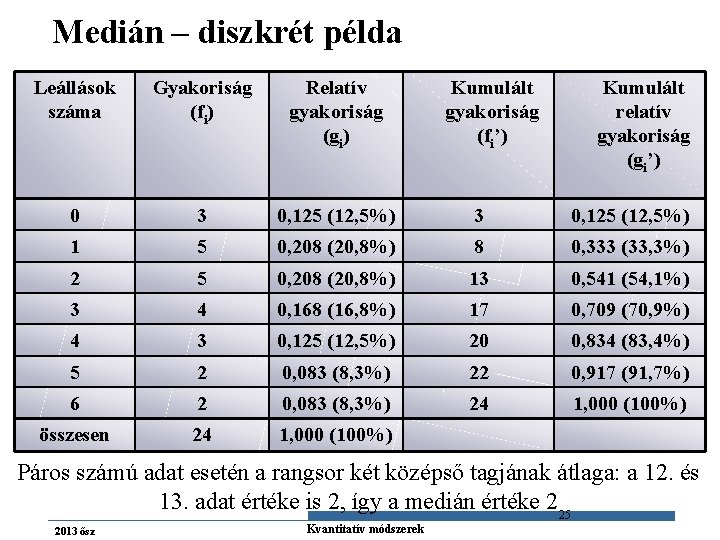
Medián – diszkrét példa Leállások száma Gyakoriság (fi) Relatív gyakoriság (gi) Kumulált gyakoriság (fi’) Kumulált relatív gyakoriság (gi’) 0 3 0, 125 (12, 5%) 1 5 0, 208 (20, 8%) 8 0, 333 (33, 3%) 2 5 0, 208 (20, 8%) 13 0, 541 (54, 1%) 3 4 0, 168 (16, 8%) 17 0, 709 (70, 9%) 4 3 0, 125 (12, 5%) 20 0, 834 (83, 4%) 5 2 0, 083 (8, 3%) 22 0, 917 (91, 7%) 6 2 0, 083 (8, 3%) 24 1, 000 (100%) összesen 24 1, 000 (100%) Páros számú adat esetén a rangsor két középső tagjának átlaga: a 12. és 13. adat értéke is 2, így a medián értéke 2 25 2013 ősz Gazdaságstatisztika Kvantitatív módszerek
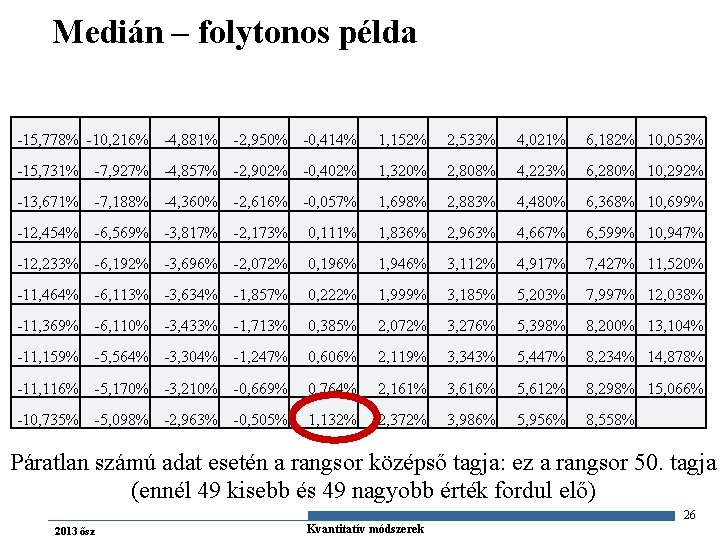
Medián – folytonos példa -15, 778% -10, 216% -4, 881% -2, 950% -0, 414% 1, 152% 2, 533% 4, 021% 6, 182% 10, 053% -15, 731% -7, 927% -4, 857% -2, 902% -0, 402% 1, 320% 2, 808% 4, 223% 6, 280% 10, 292% -13, 671% -7, 188% -4, 360% -2, 616% -0, 057% 1, 698% 2, 883% 4, 480% 6, 368% 10, 699% -12, 454% -6, 569% -3, 817% -2, 173% 0, 111% 1, 836% 2, 963% 4, 667% 6, 599% 10, 947% -12, 233% -6, 192% -3, 696% -2, 072% 0, 196% 1, 946% 3, 112% 4, 917% 7, 427% 11, 520% -11, 464% -6, 113% -3, 634% -1, 857% 0, 222% 1, 999% 3, 185% 5, 203% 7, 997% 12, 038% -11, 369% -6, 110% -3, 433% -1, 713% 0, 385% 2, 072% 3, 276% 5, 398% 8, 200% 13, 104% -11, 159% -5, 564% -3, 304% -1, 247% 0, 606% 2, 119% 3, 343% 5, 447% 8, 234% 14, 878% -11, 116% -5, 170% -3, 210% -0, 669% 0, 764% 2, 161% 3, 616% 5, 612% 8, 298% 15, 066% -10, 735% -5, 098% -2, 963% -0, 505% 1, 132% 2, 372% 3, 986% 5, 956% 8, 558% Páratlan számú adat esetén a rangsor középső tagja: ez a rangsor 50. tagja (ennél 49 kisebb és 49 nagyobb érték fordul elő) 26 2013 ősz Gazdaságstatisztika Kvantitatív módszerek
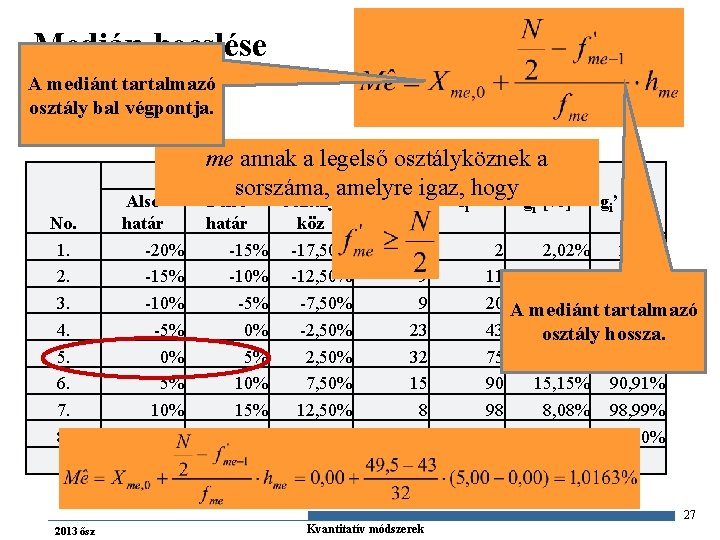
Medián becslése A mediánt tartalmazó osztály bal végpontja. me annak a legelső osztályköznek a osztály sorszáma, amelyre igaz, hogy Alsó Felső Osztályf f’ g [%] No. 1. 2. 3. 4. 5. 6. 7. 8. határ -20% -15% -10% -5% 0% 0% 5% 5% 10% 15% 20% összesen köz -17, 50% -12, 50% -7, 50% -2, 50% 7, 50% 12, 50% 17, 50% i i 2 9 9 23 32 15 8 1 99 gi’ [%] 2, 02% 9, 09% 11, 11% 9, 09% 20, 20% A mediánt tartalmazó 23, 23% 43, 43% osztály hossza. 32, 32% 75, 76% 15, 15% 90, 91% 8, 08% 98, 99% 1, 01% 100, 00% i 2 11 20 43 75 90 98 99 27 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

Módusz n n n n Helyzeti középérték – tipikus Diszkrét ismérv esetén a leggyakrabban előforduló ismérvérték Folytonos ismérv esetén pedig a gyakorisági görbe maximumhelye Nem mindig határozható meg egyértelműen, nem mindig létezik Érzéketlen a szélsőértékekre, nem függ a többi ismérvértéktől sem Becslése bizonytalan Nyers módusz 28 2013 ősz Gazdaságstatisztika Kvantitatív módszerek
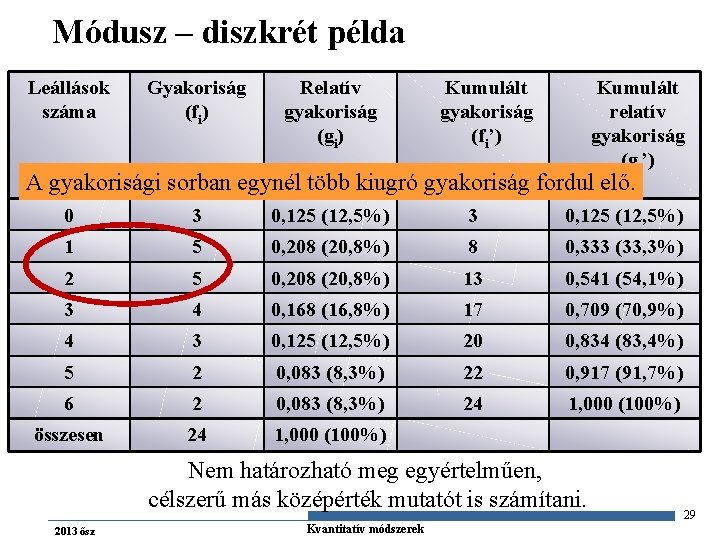
Módusz – diszkrét példa Leállások száma Gyakoriság (fi) Relatív gyakoriság (gi) Kumulált gyakoriság (fi’) Kumulált relatív gyakoriság (gi’) A gyakorisági sorban egynél több kiugró gyakoriság fordul elő. 0 3 0, 125 (12, 5%) 1 5 0, 208 (20, 8%) 8 0, 333 (33, 3%) 2 5 0, 208 (20, 8%) 13 0, 541 (54, 1%) 3 4 0, 168 (16, 8%) 17 0, 709 (70, 9%) 4 3 0, 125 (12, 5%) 20 0, 834 (83, 4%) 5 2 0, 083 (8, 3%) 22 0, 917 (91, 7%) 6 2 0, 083 (8, 3%) 24 1, 000 (100%) összesen 24 1, 000 (100%) Nem határozható meg egyértelműen, célszerű más középérték mutatót is számítani. 2013 ősz Gazdaságstatisztika Kvantitatív módszerek 29
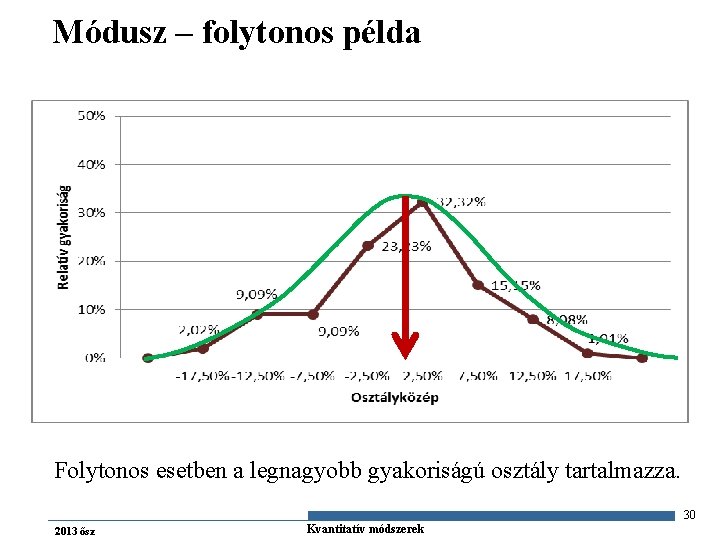
Módusz – folytonos példa Folytonos esetben a legnagyobb gyakoriságú osztály tartalmazza. 30 2013 ősz Gazdaságstatisztika Kvantitatív módszerek
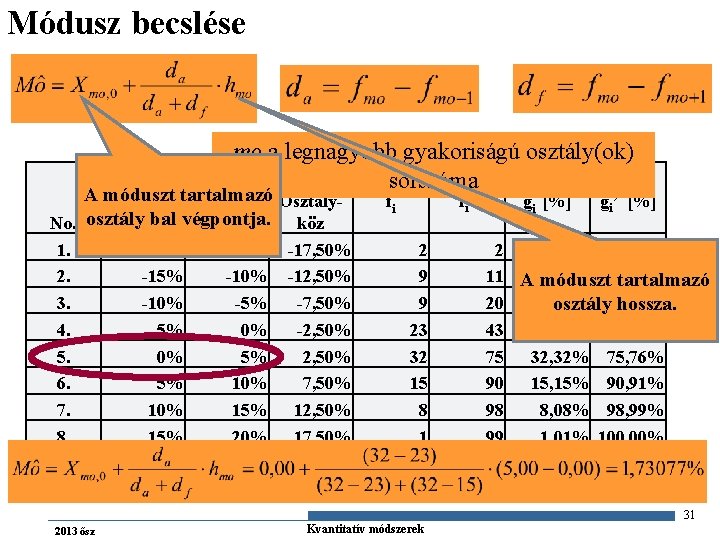
Módusz becslése mo a legnagyobb gyakoriságú osztály(ok) sorszáma No. 1. 2. 3. 4. 5. 6. 7. 8. osztály A móduszt tartalmazó Alsó Felső Osztályosztály bal végpontja. határ köz -20% -15% -17, 50% -15% -10% -12, 50% -10% -5% -7, 50% -5% 0% -2, 50% 0% 5% 2, 50% 5% 10% 7, 50% 15% 12, 50% 15% 20% 17, 50% összesen fi fi’ 2 9 9 23 32 15 8 1 99 gi [%] 2 11 20 43 75 90 98 99 gi’ [%] 2, 02% 9, 09% 11, 11% A móduszt tartalmazó 9, 09% 20, 20% osztály hossza. 23, 23% 43, 43% 32, 32% 75, 76% 15, 15% 90, 91% 8, 08% 98, 99% 1, 01% 100, 00% 31 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

Számtani átlag n Az a szám, amellyel az átlagolandó számértékeket helyettesítve azok összege változatlan marad n Leggyakrabban használt középérték n Meghatározható gyakorisági sorból is a gyakoriságokkal súlyozva n Számított középérték-mutató n Bármely alapadathalmazból egyértelműen meghatározható n Minden alapadatot felhasznál n Érzékeny a szélsőértékekre o Nyesett átlag 2013 ősz min. , ha 32 Gazdaságstatisztika Kvantitatív módszerek
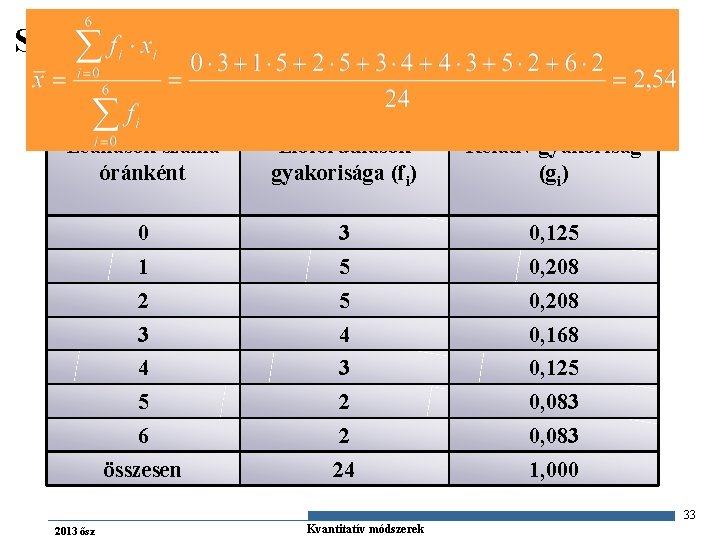
Számtani átlag –diszkrét példa Leállások száma óránként Előfordulások gyakorisága (fi) Relatív gyakoriság (gi) 0 3 0, 125 1 5 0, 208 2 5 0, 208 3 4 0, 168 4 3 0, 125 5 2 0, 083 6 2 0, 083 összesen 24 1, 000 33 2013 ősz Gazdaságstatisztika Kvantitatív módszerek
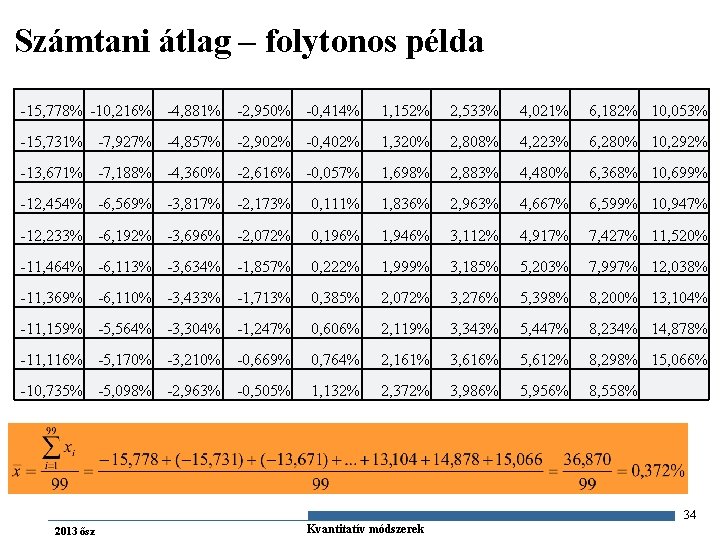
Számtani átlag – folytonos példa -15, 778% -10, 216% -4, 881% -2, 950% -0, 414% 1, 152% 2, 533% 4, 021% 6, 182% 10, 053% -15, 731% -7, 927% -4, 857% -2, 902% -0, 402% 1, 320% 2, 808% 4, 223% 6, 280% 10, 292% -13, 671% -7, 188% -4, 360% -2, 616% -0, 057% 1, 698% 2, 883% 4, 480% 6, 368% 10, 699% -12, 454% -6, 569% -3, 817% -2, 173% 0, 111% 1, 836% 2, 963% 4, 667% 6, 599% 10, 947% -12, 233% -6, 192% -3, 696% -2, 072% 0, 196% 1, 946% 3, 112% 4, 917% 7, 427% 11, 520% -11, 464% -6, 113% -3, 634% -1, 857% 0, 222% 1, 999% 3, 185% 5, 203% 7, 997% 12, 038% -11, 369% -6, 110% -3, 433% -1, 713% 0, 385% 2, 072% 3, 276% 5, 398% 8, 200% 13, 104% -11, 159% -5, 564% -3, 304% -1, 247% 0, 606% 2, 119% 3, 343% 5, 447% 8, 234% 14, 878% -11, 116% -5, 170% -3, 210% -0, 669% 0, 764% 2, 161% 3, 616% 5, 612% 8, 298% 15, 066% -10, 735% -5, 098% -2, 963% -0, 505% 1, 132% 2, 372% 3, 986% 5, 956% 8, 558% 34 2013 ősz Gazdaságstatisztika Kvantitatív módszerek
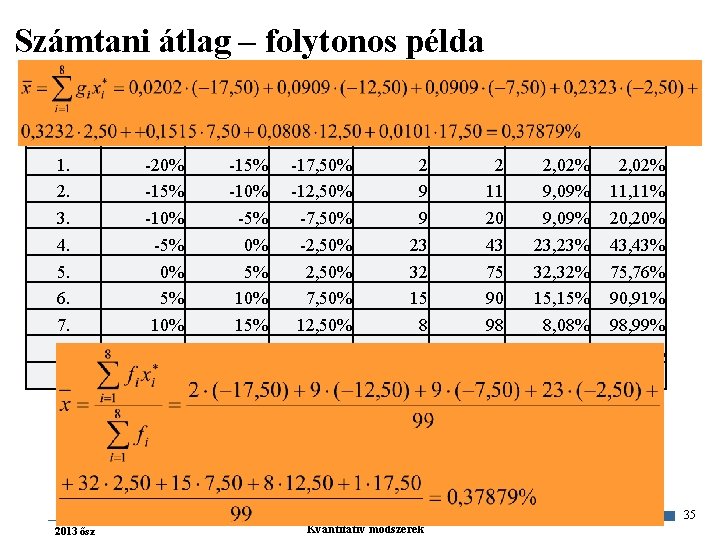
Számtani átlag – folytonos példa No. 1. 2. 3. 4. 5. 6. 7. 8. osztály Alsó Felső Osztályhatár köz -20% -15% -17, 50% -15% -10% -12, 50% -10% -5% -7, 50% -5% 0% -2, 50% 0% 5% 2, 50% 5% 10% 7, 50% 15% 12, 50% 15% 20% 17, 50% összesen fi fi’ 2 9 9 23 32 15 8 1 99 gi [%] 2 11 20 43 75 90 98 99 2, 02% 9, 09% 23, 23% 32, 32% 15, 15% 8, 08% 1, 01% 100, 00% gi’ [%] 2, 02% 11, 11% 20, 20% 43, 43% 75, 76% 90, 91% 98, 99% 100, 00% 35 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

Harmonikus átlag n A harmonikus átlag az a szám, amellyel az átlagolandó értékeket helyettesítve azok reciprokainak összege változatlan marad. Mértani átlag n A mértani átlag az a szám, amellyel az átlagolandó értékeket helyettesítve azok szorzata változatlan marad. 36 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

Négyzetes átlag n Az a szám, amellyel az átlagolandó értékeket helyettesítve, azok négyzetösszege változatlan marad n Tipikus alkalmazási területe a szórásszámítás Választás a középértékek között 37 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

Választás a középértékek között n Módusz, medián, számtani átlag? n Melyiket használjuk? o Egyértelműen meghatározható-e? o Az összes rendelkezésre álló adattól függ-e vagy sem? o Mennyire érzékeny a szélsőségesen nagy vagy kicsi értékekre? o Mekkora és milyen módon értelmezhető hibával képes helyettesíteni az alapadatokat? 38 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

Választás a középértékek között n Medián o o o n Módusz o o o n Egyértelműen meghatározható, mindig létezik Ha sok az egyforma ismérvérték, akkor nem tanácsos használni Nem függ sem az összes értéktől, sem a szélsőséges értékektől Nem mindig határozható meg egyértelműen, nem is mindig létezik Becslése bizonytalan (függ az osztályok kialakításától) Nem függ sem az összes értéktől, sem a szélsőséges értékektől Számtani átlag o o o Bármely alapadathalmazból egyértelműen meghatározható, minden alapadatot felhasznál, mindig létezik Érzékeny a szélsőséges értékekre nyesett átlag Nem feltétlen tipikus érték 39 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

Kvantilisek n Eddig egyenlő osztályköz-hosszúságú gyakorisági sorokat képeztünk, amelyeknek eltért a relatív gyakorisága. A kvantilisek olyan „osztópontok”, amelynek segítségével a növekvő sorrendbe állított adataink egyenlő gyakoriságú osztályokra bonthatóak Jelölése: Xi/k o i-edik k-ad rendű kvantilis: az a szám, amelynél az összes előforduló ismérvérték i/k-ad része kisebb , (1 -i/k)-ad része pedig nagyobb (i=1, . . , k-1 és k>=2) A rangsor si/k. tagja n Értéke n n n 40 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

A legfontosabb kvantilisek k Elnevezés Általános jelölés i lehetséges értéke Lehetséges kvantilisek 2 Medián - 1 Me 4 Kvartilis Qi 1, 2, 3 Q 1, Q 2, Q 3 5 Kvintilis Ki 1, 2, 3, 4, K 1, K 2, K 3, K 4 10 Decilis Di 1, 2, …, 9 D 1, D 2, … D 9 100 Percentilis Pi 1, 2, …, 99 P 1, P 2, …, P 99 41 2013 ősz Gazdaságstatisztika Kvantitatív módszerek
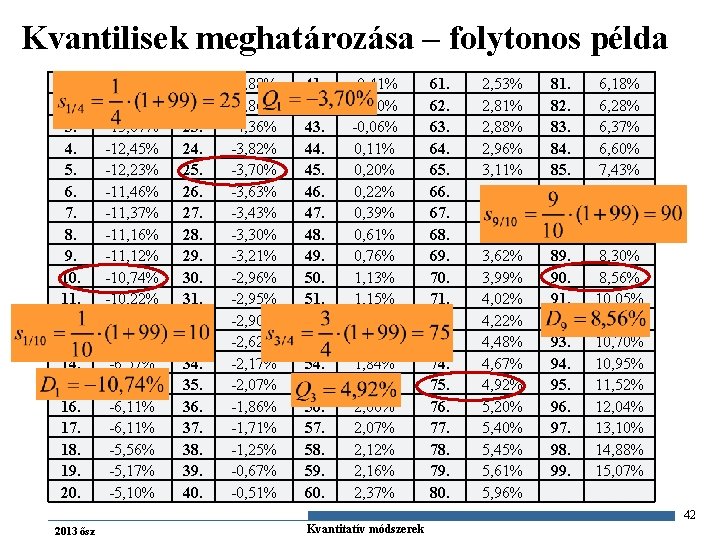
Kvantilisek meghatározása – folytonos példa 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. -15, 78% -15, 73% -13, 67% -12, 45% -12, 23% -11, 46% -11, 37% -11, 16% -11, 12% -10, 74% -10, 22% -7, 93% -7, 19% -6, 57% -6, 19% -6, 11% -5, 56% -5, 17% -5, 10% 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39. 40. -4, 88% -4, 86% -4, 36% -3, 82% -3, 70% -3, 63% -3, 43% -3, 30% -3, 21% -2, 96% -2, 95% -2, 90% -2, 62% -2, 17% -2, 07% -1, 86% -1, 71% -1, 25% -0, 67% -0, 51% 41. 42. 43. 44. 45. 46. 47. 48. 49. 50. 51. 52. 53. 54. 55. 56. 57. 58. 59. 60. -0, 41% -0, 40% -0, 06% 0, 11% 0, 20% 0, 22% 0, 39% 0, 61% 0, 76% 1, 13% 1, 15% 1, 32% 1, 70% 1, 84% 1, 95% 2, 00% 2, 07% 2, 12% 2, 16% 2, 37% 61. 62. 63. 64. 65. 66. 67. 68. 69. 70. 71. 72. 73. 74. 75. 76. 77. 78. 79. 80. 2, 53% 2, 81% 2, 88% 2, 96% 3, 11% 3, 19% 3, 28% 3, 34% 3, 62% 3, 99% 4, 02% 4, 22% 4, 48% 4, 67% 4, 92% 5, 20% 5, 45% 5, 61% 5, 96% 81. 82. 83. 84. 85. 86. 87. 88. 89. 90. 91. 92. 93. 94. 95. 96. 97. 98. 99. 6, 18% 6, 28% 6, 37% 6, 60% 7, 43% 8, 00% 8, 23% 8, 30% 8, 56% 10, 05% 10, 29% 10, 70% 10, 95% 11, 52% 12, 04% 13, 10% 14, 88% 15, 07% 42 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

Ingadozásmutatók n Osztályozásuk: o Kitüntetett értéktől vett eltérés vagy egymástól vett eltérés o Abszolút vagy relatív n terjedelem n átlagos abszolút különbség n átlagos abszolút eltérés n szórás n relatív szórás 43 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

Terjedelemmutatók 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. -15, 78% -15, 73% -13, 67% -12, 45% -12, 23% -11, 46% -11, 37% -11, 16% -11, 12% -10, 74% -10, 22% -7, 93% -7, 19% -6, 57% -6, 19% -6, 11% -5, 56% -5, 17% -5, 10% 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39. 40. -4, 88% -4, 86% -4, 36% -3, 82% -3, 70% -3, 63% -3, 43% -3, 30% -3, 21% -2, 96% -2, 95% -2, 90% -2, 62% -2, 17% -2, 07% -1, 86% -1, 71% -1, 25% -0, 67% -0, 51% 41. 42. 43. 44. 45. 46. 47. 48. 49. 50. 51. 52. 53. 54. 55. 56. 57. 58. 59. 60. -0, 41% -0, 40% -0, 06% 0, 11% 0, 20% 0, 22% 0, 39% 0, 61% 0, 76% 1, 13% 1, 15% 1, 32% 1, 70% 1, 84% 1, 95% 2, 00% 2, 07% 2, 12% 2, 16% 2, 37% 61. 62. 63. 64. 65. 66. 67. 68. 69. 70. 71. 72. 73. 74. 75. 76. 77. 78. 79. 80. 2, 53% 2, 81% 2, 88% 2, 96% 3, 11% 3, 19% 3, 28% 3, 34% 3, 62% 3, 99% 4, 02% 4, 22% 4, 48% 4, 67% 4, 92% 5, 20% 5, 45% 5, 61% 5, 96% 81. 82. 83. 84. 85. 86. 87. 88. 89. 90. 91. 92. 93. 94. 95. 96. 97. 98. 99. 6, 18% 6, 28% 6, 37% 6, 60% 7, 43% 8, 00% 8, 23% 8, 30% 8, 56% 10, 05% 10, 29% 10, 70% 10, 95% 11, 52% 12, 04% 13, 10% 14, 88% 15, 07% 44 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

Átlagos abszolút különbség (G) n Az átlagos abszolút különbség a minden lehetséges módon párba állított ismérvértékek különbségeinek abszolút értékéből számított számtani átlag. n Azt mutatja meg, hogy az X ismérv értékei átlagosan mennyire különböznek egymástól. Felhasználási területe: koncentrációelemzés n 45 52 76 87 92 45 0 7 31 42 47 52 7 0 24 35 40 76 31 24 0 11 16 87 42 35 11 0 5 92 47 40 16 5 0 Az 5 hallgató zh-n elért pontja átlagosan 25, 8 ponttal tér el egymástól. 45 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

Átlagos abszolút eltérés (Δ) n n Az átlagos abszolút eltérés az egyes ismérvértékek és a számtani átlag különbségeinek abszolút értékeiből számított számtani átlag. Súlyozott formula: leállások száma óránként 0 1 2 3 4 5 6 összesen az előfordulások gyakorisága 3 5 5 4 3 2 2 24 A gépleállások átlagosan 1, 503 -al térnek el az átlagtól. 46 2013 ősz Gazdaságstatisztika Kvantitatív módszerek
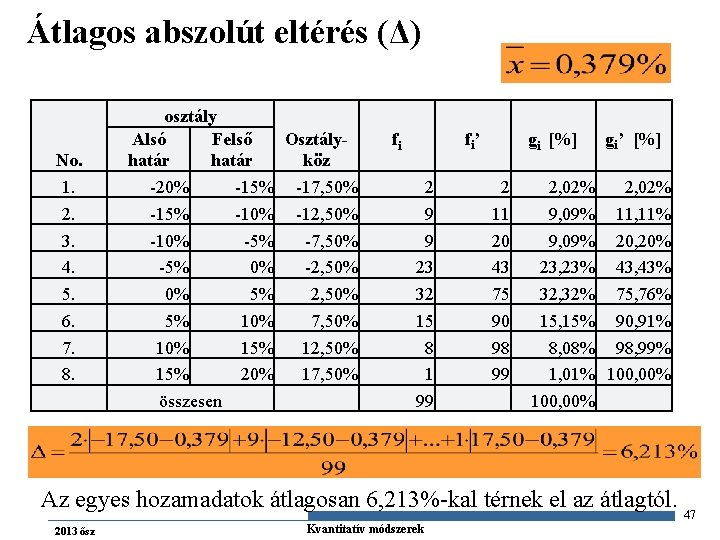
Átlagos abszolút eltérés (Δ) No. 1. 2. 3. 4. 5. 6. 7. 8. osztály Alsó Felső Osztályhatár köz -20% -15% -17, 50% -15% -10% -12, 50% -10% -5% -7, 50% -5% 0% -2, 50% 0% 5% 2, 50% 5% 10% 7, 50% 15% 12, 50% 15% 20% 17, 50% összesen fi fi’ 2 9 9 23 32 15 8 1 99 gi [%] 2 11 20 43 75 90 98 99 2, 02% 9, 09% 23, 23% 32, 32% 15, 15% 8, 08% 1, 01% 100, 00% gi’ [%] 2, 02% 11, 11% 20, 20% 43, 43% 75, 76% 90, 91% 98, 99% 100, 00% Az egyes hozamadatok átlagosan 6, 213%-kal térnek el az átlagtól. 2013 ősz Gazdaságstatisztika Kvantitatív módszerek 47

Tapasztalati szórás n n n abszolút érték helyett négyzetre emelés és gyökvonás A szórás az egyes Xi ismérvértékek átlagtól vett di eltéréseinek négyzetes átlaga. Azt mutatja, hogy az egyes értékek átlagosan mennyire térnek el a számtani átlagtól. Olyan átlagos hibaként is felfogható, amit akkor követünk el, ha minden adatot a számtani átlaggal helyettesítünk. Csak akkor 0, ha minden ismérvérték egyenlő. Érzékeny a kiugró értékekre. 48 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

Korrigált tapasztalati szórás n A szórás torzítatlan becsléssel n a becslés a szóban forgó paraméterérték körül ingadozzék. n a becslés (az illető statisztika) várható értéke éppen a megfelelő paraméterérték legyen. n a korrigált tapasztalati szórásnégyzet várható értéke az elméleti varianciával egyenlő, a tapasztalati szórásnégyzet az elméleti variancia torzított becslése 49 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

Tapasztalati szórás leállások száma óránként 0 1 2 3 4 5 6 összesen az előfordulások gyakorisága 3 5 5 4 3 2 2 24 Az óránkénti leállások száma 1, 779 db-bal tér el az átlagtól. 2013 ősz Gazdaságstatisztika Kvantitatív módszerek 50
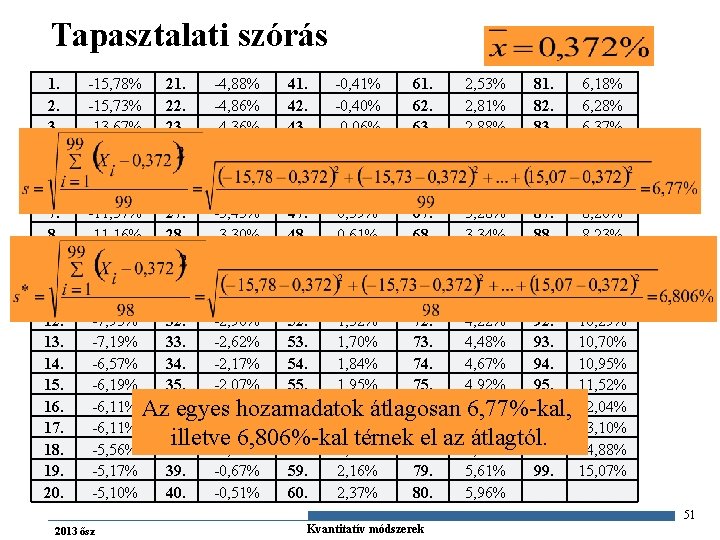
Tapasztalati szórás 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. -15, 78% 21. -4, 88% 41. -0, 41% 61. 2, 53% 81. 6, 18% -15, 73% 22. -4, 86% 42. -0, 40% 62. 2, 81% 82. 6, 28% -13, 67% 23. -4, 36% 43. -0, 06% 63. 2, 88% 83. 6, 37% -12, 45% 24. -3, 82% 44. 0, 11% 64. 2, 96% 84. 6, 60% -12, 23% 25. -3, 70% 45. 0, 20% 65. 3, 11% 85. 7, 43% -11, 46% 26. -3, 63% 46. 0, 22% 66. 3, 19% 86. 8, 00% -11, 37% 27. -3, 43% 47. 0, 39% 67. 3, 28% 87. 8, 20% -11, 16% 28. -3, 30% 48. 0, 61% 68. 3, 34% 88. 8, 23% -11, 12% 29. -3, 21% 49. 0, 76% 69. 3, 62% 89. 8, 30% -10, 74% 30. -2, 96% 50. 1, 13% 70. 3, 99% 90. 8, 56% -10, 22% 31. -2, 95% 51. 1, 15% 71. 4, 02% 91. 10, 05% -7, 93% 32. -2, 90% 52. 1, 32% 72. 4, 22% 92. 10, 29% -7, 19% 33. -2, 62% 53. 1, 70% 73. 4, 48% 93. 10, 70% -6, 57% 34. -2, 17% 54. 1, 84% 74. 4, 67% 94. 10, 95% -6, 19% 35. -2, 07% 55. 1, 95% 75. 4, 92% 95. 11, 52% -6, 11% Az egyes hozamadatok átlagosan 6, 77%-kal, 36. -1, 86% 56. 2, 00% 76. 5, 20% 96. 12, 04% -6, 11% 37. -1, 71% 57. 2, 07% 77. 5, 40% 97. 13, 10% illetve 6, 806%-kal térnek el az átlagtól. -5, 56% 38. -1, 25% 58. 2, 12% 78. 5, 45% 98. 14, 88% -5, 17% 39. -0, 67% 59. 2, 16% 79. 5, 61% 99. 15, 07% -5, 10% 40. -0, 51% 60. 2, 37% 80. 5, 96% 51 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

Tapasztalati szórás No. 1. 2. 3. 4. 5. 6. 7. 8. osztály Alsó Felső Osztályhatár köz -20% -15% -17, 50% -15% -10% -12, 50% -10% -5% -7, 50% -5% 0% -2, 50% 0% 5% 2, 50% 5% 10% 7, 50% 15% 12, 50% 15% 20% 17, 50% összesen fi fi’ 2 9 9 23 32 15 8 1 99 gi [%] 2 11 20 43 75 90 98 99 2, 02% 9, 09% 23, 23% 32, 32% 15, 15% 8, 08% 1, 01% 100, 00% gi’ [%] 2, 02% 11, 11% 20, 20% 43, 43% 75, 76% 90, 91% 98, 99% 100, 00% 52 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

Relatív szórás n n n Különböző mértékegységű sorozatok szóródásának összehasonlítására pozitív értékű ismérvekre! az ismérvértékek átlagtól vett átlagos relatív eltérése Nincs mértékegysége! Minél kisebb az értéke, a számtani átlag annál jobb középérték leállások száma óránként 0 1 2 3 4 5 6 összesen az előfordulások gyakorisága 3 5 5 4 3 2 2 24 53 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

Alakmutatók n A gyakorisági eloszlás milyen mértékben tér el az ún. normális eloszlástól n Eltérés lehet: o Bal ill. jobb oldali aszimmetria o Csúcsosság vagy lapultság 54 2013 ősz Gazdaságstatisztika Kvantitatív módszerek

Pearson-féle mutatószám Negatív P esetén jobboldali az aszimmetria (átlag<medián). Csúcsossági mutató Normális eloszlás esetén értéke 0, 263. Minél laposabb, annál nagyobb K értéke. 55 2013 ősz Gazdaságstatisztika Kvantitatív módszerek
- Slides: 55












































































