KVADRATICK NEROVNICE 1 Kvadratick nerovnice a jejich algebraick

KVADRATICKÉ NEROVNICE 1. Kvadratické nerovnice a jejich algebraické a grafické řešení 2. Kvadratické nerovnice s neznámou ve jmenovateli 3. Kvadratické nerovnice s parametrem 4. Kvadratické nerovnice s absolutními hodnotami

Kvadratická nerovnice s neznámou x є R je každá nerovnice tvaru ax 2+ bx + c > 0 nebo ax 2+ bx + c ≥ 0 nebo ax 2+ bx + c < 0 nebo ax 2+ bx + c ≤ 0, kde a, b, c jsou reálné koeficienty, a ≠ 0.

Příklad 1 Řešte v R kvadratickou nerovnici: 2 x - 6 x - 7 > 0

1. najdeme kořeny kvadratické rovnice x 2 - 6 x - 7 = 0 a) řešení pomocí Viètových vzorců

b) řešení pomocí výpočtu diskriminantu

2. zadanou nerovnici upravíme na součinný tvar (x +1)(x – 7) > 0 a) algebraické řešení - porovnáváme součin dvou činitelů s nulou: (x + 1)(x – 7) > 0 právě tehdy, když [x+1>0 x– 7>0] [ x + 1< 0 x– 7<0]

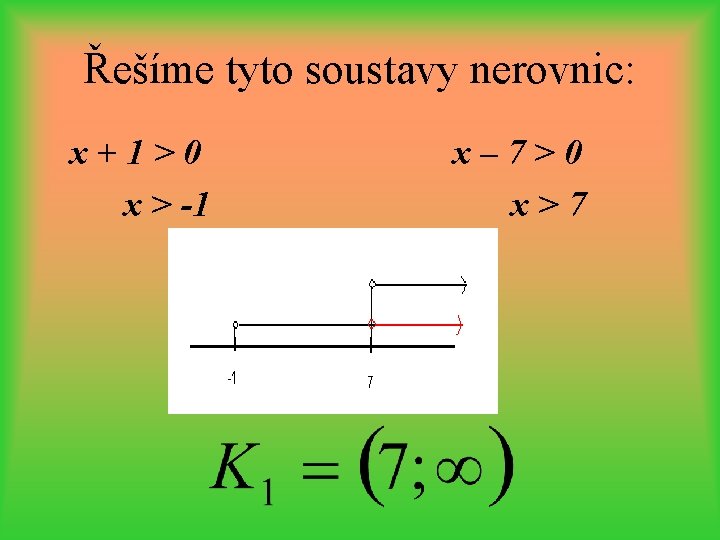
Řešíme tyto soustavy nerovnic: x+1>0 x > -1 x– 7>0 x>7

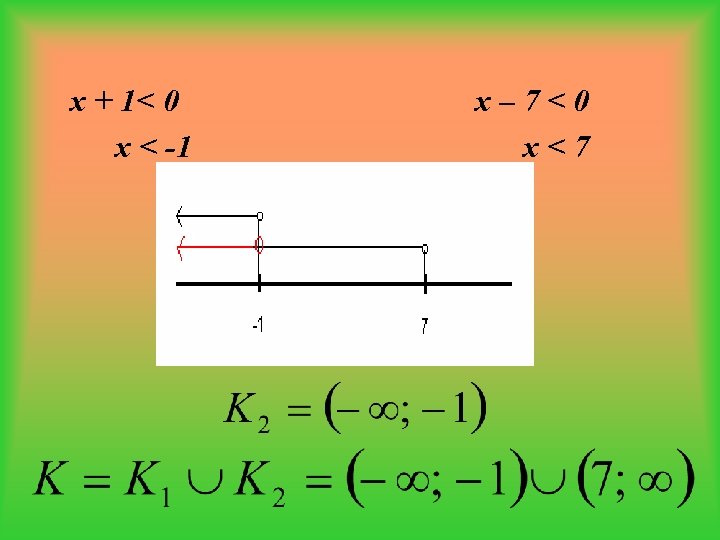
x + 1< 0 x < -1 x– 7<0 x<7

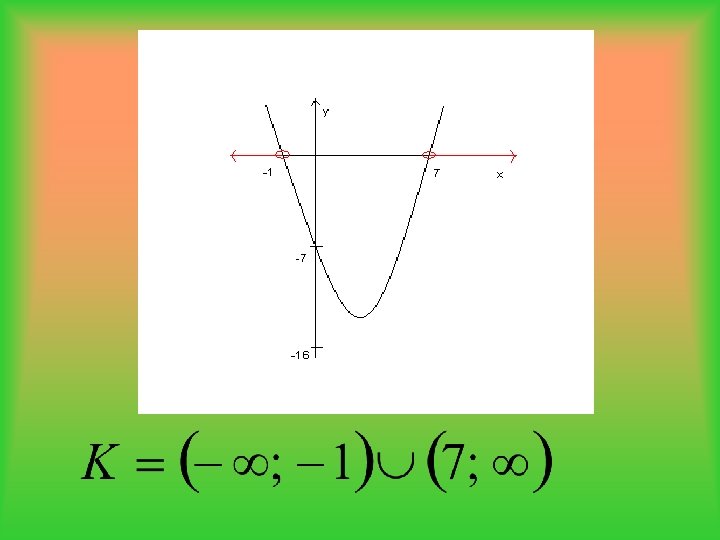
b) grafické řešení Nakreslíme graf kvadratické funkce y = x 2– 6 x– 7. Víme, že osu x kartézské soustavy souřadnic protíná v bodech [7; 0] a [-1; 0] a podle koeficientu a=1>0 víme, že ve vrcholu má funkce svoji minimální funkční hodnotu. Přesné souřadnice vrcholu ani zjišťovat nemusíme. Z obrázku je patrné, že funkční hodnoty této kvadratické funkce jsou větší než nula pro , protože graf funkce leží v těchto intervalech nad osou x.

Řešte nerovnice v R: a) x 2 – 5 x + 6 < 0 e) 4 x – 4 x 2 – 5 > 0 b) 3 x 2 + 5 x > 0 f) 7 x 2 + 19 x – 6 ≤ 0 c) x 2 + 14 x + 49 ≥ 0 g) 2 – 5 x - 3 x 2 ≤ 0 d) 5 x - x 2 – 6, 25 ≥ 0 h) 2 x 2 – 7 x < 0

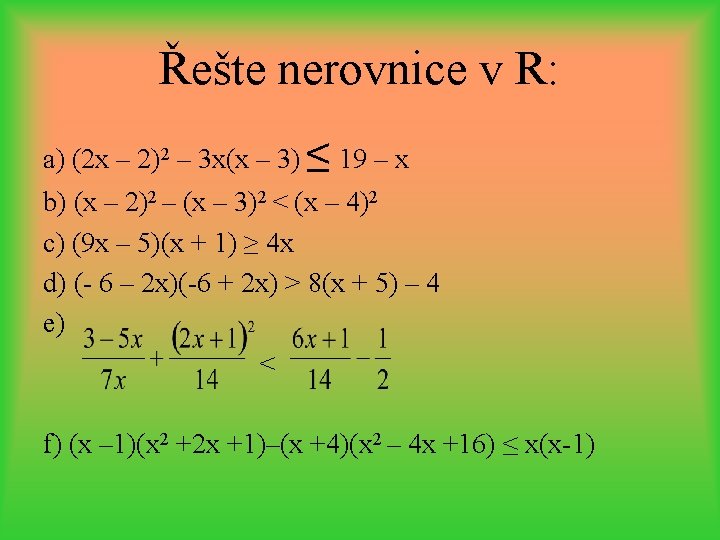
1. Upravíme na podílový tvar 2. Řešíme kvadratickou nerovnici způsobem popsaným v kapitole 1

Příklad 2 Řešte v R nerovnici:

Úprava na podílový tvar znamená upravit nerovnici tak, abychom na jedné straně získali výraz ve tvaru podílu (lomený výraz), na druhé straně nerovnice 0.

Výraz x 2 + 1 nabývá pro každé x є R pouze nezáporných hodnot, proto jím můžeme nerovnici vynásobit beze změny znaménka.

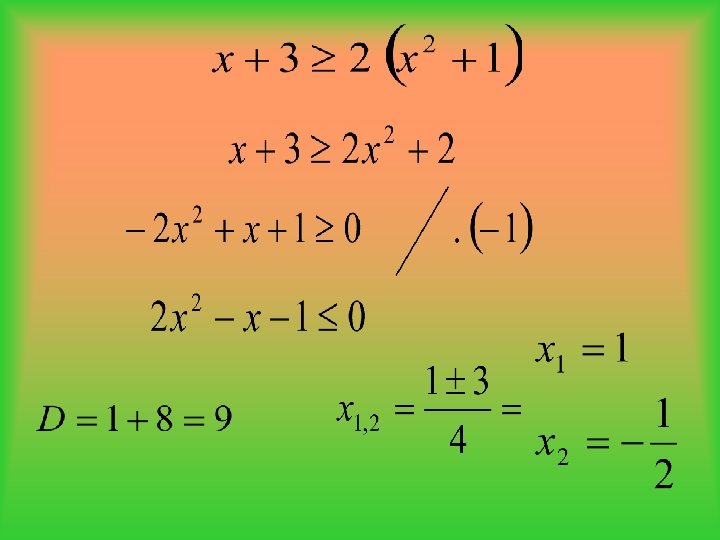
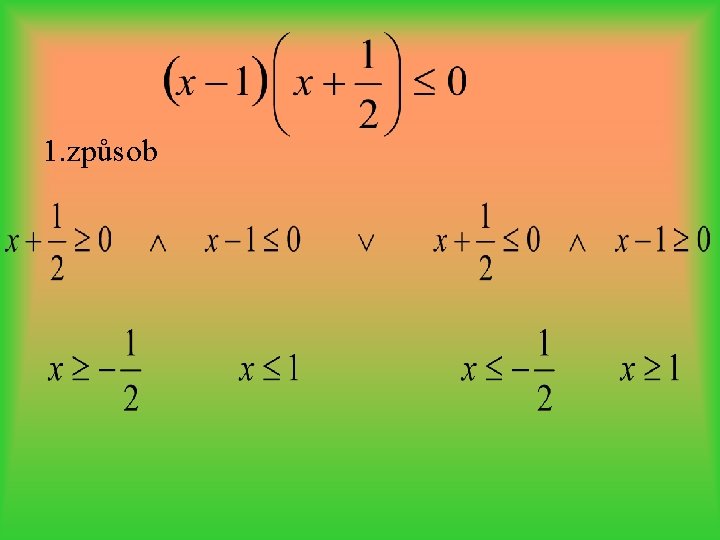
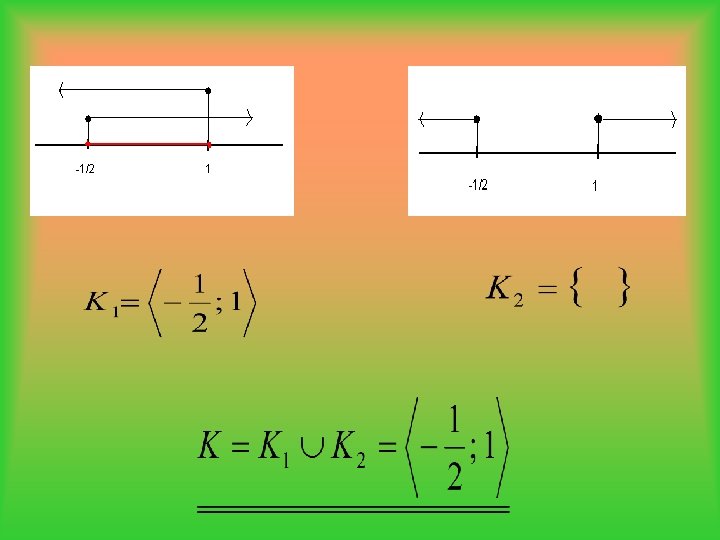
1. způsob

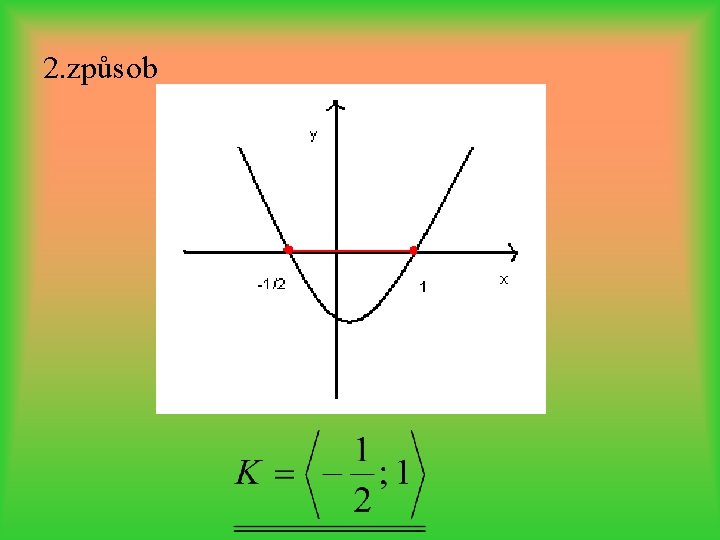
2. způsob