Kurs Statistika u psihologiji 1 Transformacije kvantitativnih podataka

Kurs: Statistika u psihologiji 1 Тема: Transformacije kvantitativnih podataka Copyright Лазар Тењовић (Lazar Tenjović) Odeljenje za psihologiju, Filozofski fakultet, Beograd

Kurs: Statistika u istraživanju obrazovanja Тема: Transformacije kvantitativnih podataka Copyright Лазар Тењовић (Lazar Tenjović) Odeljenje za psihologiju, Filozofski fakultet, Beograd

Zašto transformišemo podatke? l Iz praktičnih razloga: bolje i lakše razumevanje podataka; l Iz statističkih razloga: – “peglanje” distribucije varijable (npr. simetrizovanje, normalizovanje); – ujednačavanje varijabilnosti različitih grupa u uzorku; – “linearizovanje” veze izmedju varijabli. Transformacije o kojima ćemo danas govoriti ne obuhvataju grupisanje sirovih podataka sa kvantitativne varijable u razredne intervale.

Transformišemo podatke često i u svakodnevnom životu l Dužinu l C u inčima u centimetre (1 in = 2. 54 cm); = (5/9)( F-32) : 100 F = 37. 8 C. l IQ (KI): Količnik inteligencije kada hoćemo da kažemo koliko smo inteligentni IQ = (MU/KU)*100 IQ = 100 + 15*zi

Vrste transformacija kvantitativnih izvornih podataka (prema Horst, 1966) l Algebarske: pomoću funkcija f: xi T(xi) l Površinske: – Percentili – Nelinearne (npr. kvadratne, logaritamske) – Linearne (npr. centriranje, standardizacija) – Percentilni rangovi – Normalizovani skorovi

Nelinearne transformacije l Stepena transformacija: l l a, b, c, d R Da bi se očuvao originalni redosled podataka: za p > 0 treba da bude i a > 0, a za p < 0, treba da bude i a < 0 Stepene transformacije se mogu koristiti za “simetrizovanje” asimetrične raspodele

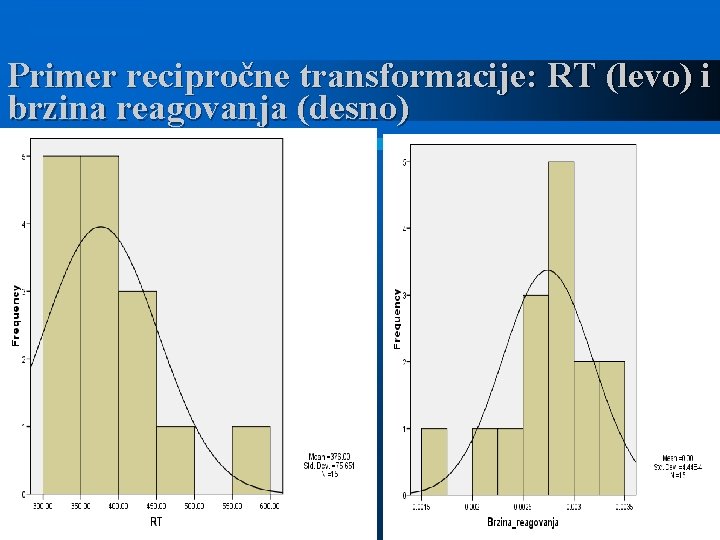
Najčešće stepene transformacije 1. Recipročna (a = 1, b = 0, p = -1): Česte u eksperimentalnoj psihologiji: vreme reakcije se transformiše u brzinu reagovanja

Primer recipročne transformacije: RT (levo) i brzina reagovanja (desno)

Najčešće stepene transformacije 2. Kvadratna (a = 1, b = 0, p = 2):

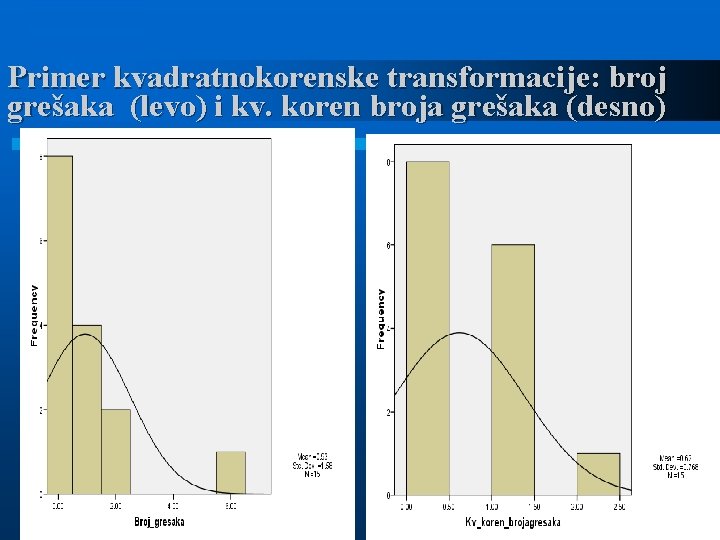
Najčešće stepene transformacije 3. Kvadratnokorenska transformacija (a = 1, b = 0, p = 1/2): “Simetrizuje” pozitivno asimetričnu distribuciju: npr. broj grešaka kad ima malo grešaka

Primer kvadratnokorenske transformacije: broj grešaka (levo) i kv. koren broja grešaka (desno)

Najčešće stepene transformacije 4. Logaritamska (p = 0, a = 1, b = 0, c = 1, d =0): Najčešće, logaritam sa osnovom e ili 10. U programu SPSS funkcije za osnovu e (Ln) i 10 (Lg 10)

Neke važne osobine nelinearnih transformacija 1. Nelinearno transformisani rezultati mogu imati potpuno drugačiji oblik distribucije od izvornih, netransformisanih rezultata. 2. Aritmetička sredina nelinearno transformisanih rezultata nije jednaka nelinearno transformisanoj aritmetičkoj sredini izvornih rezultata! Nelinearne transformacije mogu dovesti do statističkih zaključaka koji su sasvim drugačiji od onih do kojih bismo došli na osnovu izvornih podataka

Neke važne osobine nelinearnih transformacija 3. Medijana nelinearno transformisanih rezultata najčešće je jednaka nelinearno transformisanoj medijani izvornih rezultata! Primer: Izvorni rezultati: 3, 4, 5, 5, 8 (M = 5, Mdn = 5) Kvadrirani rezultati: 9, 16, 25, 64 (Mt= 27. 8, Mdnt = 25) Dakle: Mt ≠ M 2, a Mdnt = Mdn 2

Linearne transformacije Opšti oblik: pri čemu je T(xi) transformisani rezultat, xi izvorni rezultat, a je aditivna konstanta, dok je b multiplikativna konstanta. Linearne transformacije služe, pre svega, da dobijemo distribuciju rezultata sa željenom vrednošću aritmetičke sredine i standardne devijacije. Ponekad pomažu da bolje razumemo rezultat određenog ispitanika.

Najčešće linearne transformacije 1. Centriranje (pretvaranje u devijacione skorove): pri čemu je di centrirani rezultat, xi izvorni rezultat, a M je aritmetička sredina izvornih rezultata. Aritmetička sredina centriranih rezultata je 0, a standardna devijacija centriranih rezultata jednaka je standardnoj devijaciji izvornih rezultata.

Najčešće linearne transformacije 2. Standardizovanje (pretvaranje u z- skorove): pri čemu je zi standardizovani rezultat, xi izvorni rezultat, M je aritmetička sredina izvornih rezultata, a S standardna devijacija izvornih rezultata. Aritmetička sredina standardizovanih rezultata je 0, a standardna devijacija standardizovanih rezultata jednaka je 1.

Najčešće linearne transformacije 3. Pretvaranje u T- skorove): Aritmetička sredina T-skorova jednaka je 50, a standardna devijacija T-skorova jednaka je 10. T-skorovi se najviše koriste u kliničkoj psihologiji.

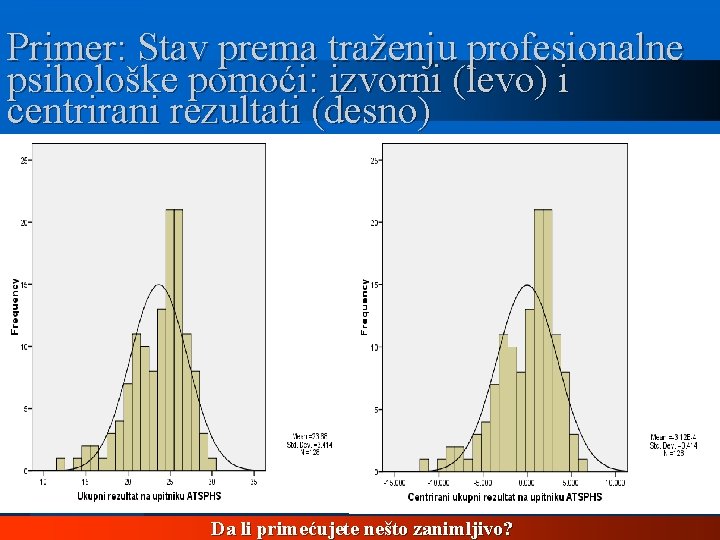
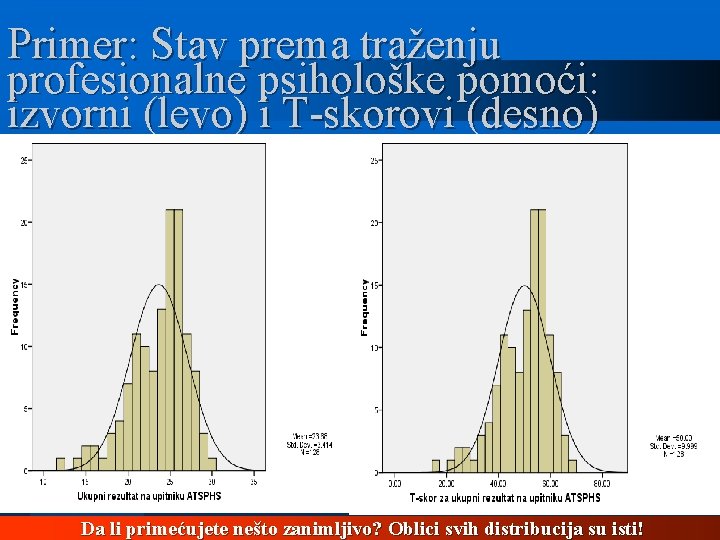
Primer: Stav prema traženju profesionalne psihološke pomoći: izvorni (levo) i centrirani rezultati (desno) Da li primećujete nešto zanimljivo?

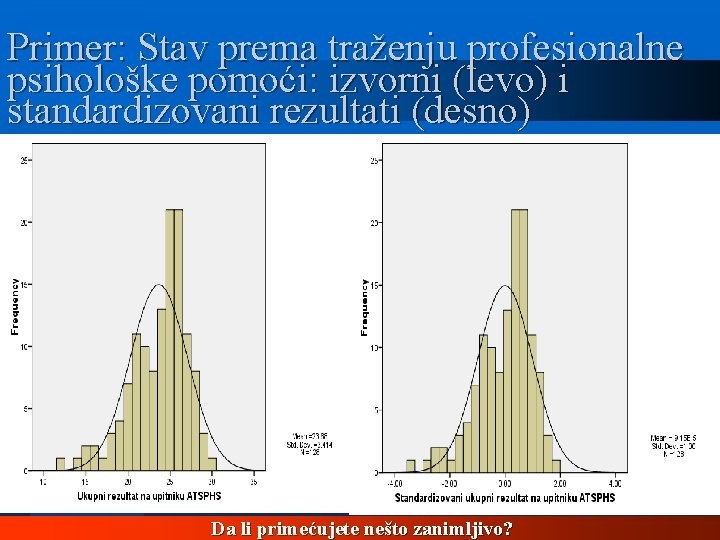
Primer: Stav prema traženju profesionalne psihološke pomoći: izvorni (levo) i standardizovani rezultati (desno) Da li primećujete nešto zanimljivo?

Primer: Stav prema traženju profesionalne psihološke pomoći: izvorni (levo) i T-skorovi (desno) Da li primećujete nešto zanimljivo? Oblici svih distribucija su isti!

Neke važne osobine linearnih transformacija 1. Linearno transformisani rezultati imaju potpuno isti oblik distribucije kao i izvorni, netransformisani rezultati. 2. Aritmetička sredina linearno transformisanih rezultata jednaka je: a + b* aritmetička sredina izvornih rezultata. 3. Standardna devijacija linearno transformisanih rezultata jednaka je: b* standardna devijacija izvornih rezultata.

Linearne transformacije: drugi pogled Opšti oblik: pri čemu je T(xi) transformisani rezultat, xi izvorni rezultat, a je aditivna konstanta, dok je b multiplikativna konstanta. Kako odrediti a i b tako da linearno transformisani rezultati imaju određene željene vrednosti aritmetičke sredine i standardne devijacije?

Određivanje odgovarajuće linearne transformacije: koeficijenti a i b M i S su aritmetička sredina i standardna devijacija izvornih rezultata, Mt i St su aritmetička sredina i standardna devijacija kakve želimo da postignemo linearnom transformacijom izvornih rezultata. Gornji obrasci za a i b slede na osnovu sledećih pravila: (1) Mt = a + b*M (2) St = b* S

Drugi pogled na prikazane linearne transformacije 1. Centriranje: da bi bilo Mt = 0, St = S, treba da bude: a = -M, b = 1. 2. Standardizovanje: da bi bilo Mt = 0, St = 1, treba da bude: a = -M/S, b = 1/S. 3. Pretvaranje u T-skorove: da bi bilo Mt = 50, St = 10, treba da bude a = 50 -(10/S)*M, b = 10/S. Savetujem da uzmete papir i olovku i ovo izvedete na osnovu obrazaca

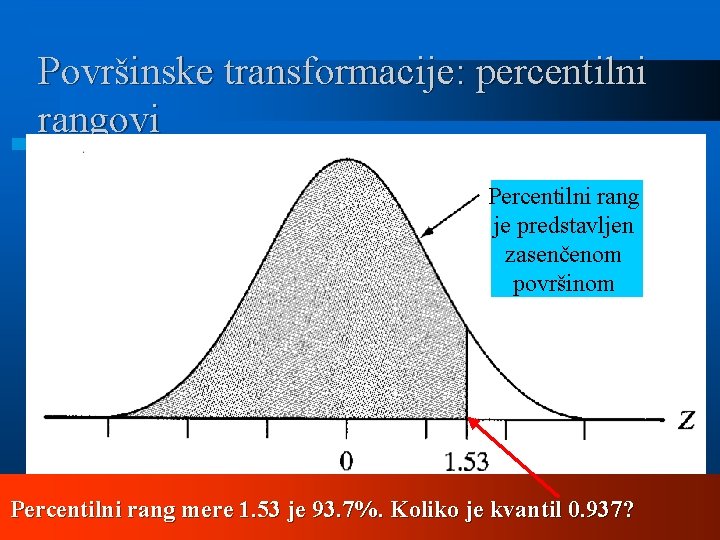
Površinske transformacije: percentilni rangovi Percentilni rang je predstavljen zasenčenom površinom Percentilni rang mere 1. 53 je 93. 7%. Koliko je kvantil 0. 937?

Površinske transformacije Pretvaranje izvornih rezultata u percentilne rangove: 1. Za mere iz grupisane raspodele: pri čemu je xi mera za koju tražimo percentilni rang, n je veličina uzorka, cfk-1 kumulativna frekvencija u razredu ispod onog u kojem je mera xi, Dk donja egzaktna granica razreda u kojem je mera xi, i veličina razrednog intervala, a fk frekvencija u razredu u kojem je mera xi.

Površinske transformacije Pretvaranje izvornih rezultata u percentilne rangove: Za negrupisane mere (i u programu SPSS): pri čemu je xi mera za koju tražimo percentilni rang, Rxi uzlazni rang mere xi, a n veličina uzorka.

Površinske transformacije Pretvaranje izvornih rezultata u percentilne rangove: Za negrupisane mere (i u programu SPSS): pri čemu je xi mera za koju tražimo percentilni rang, Rxi uzlazni rang mere xi, a n veličina uzorka.

Transformisati ili ne-pitanje je sad! l Linearne transformacije često su neophodne kako bi rezultati dobili svoje jasno značenje. l Pri korišćenju nelinearnih transformacija treba biti oprezan: ukoliko se transformacija preduzima radi postizanja nekog željenog oblika distribucije treba imati u vidu da je potrebno da rezultati u transformisanom obliku imaju neki sadržinski smisao i da se može pretpostaviti da varijabla u populaciji ima željeni oblik. l Posebno treba biti oprezan u situacijama kada su statistički zaključci do kojih dolazimo na osnovu izvornih i transformisanih rezultata sasvim drugačiji, čak suprotni.