Kuliah Rangkaian Digital Kuliah 4 Analisis Rangkaian Kombinasional

Kuliah Rangkaian Digital Kuliah 4: Analisis Rangkaian Kombinasional Teknik Komputer Universitas Gunadarma 1

Topik 4 – Analisis Rangkaian Kombinasional Rangkaian-2 logika kombinasional: n n n Keluaran-2 tergantung hanya pada masukan-2 nya. Tidak terdapat loop umpan balik (feedback loops) Dideskripsikan dgn menngunakan ekspresi-2 Boolean dan/atau tabel-2 kebenaran. Rangkaian-2 logika sekuensial: n n n Keluaran-2 tidak hanya tergantung pada masukan-2 nya, tetapi juga pada masukan-2 masa lampua (the past sequence of inputs). Mengandung logika kombinasional dan elemen-2 memory yang terbentuk melalui “feedback loops” Dideskripsikan dengan “state transition tables” dan “diagram-2” 2

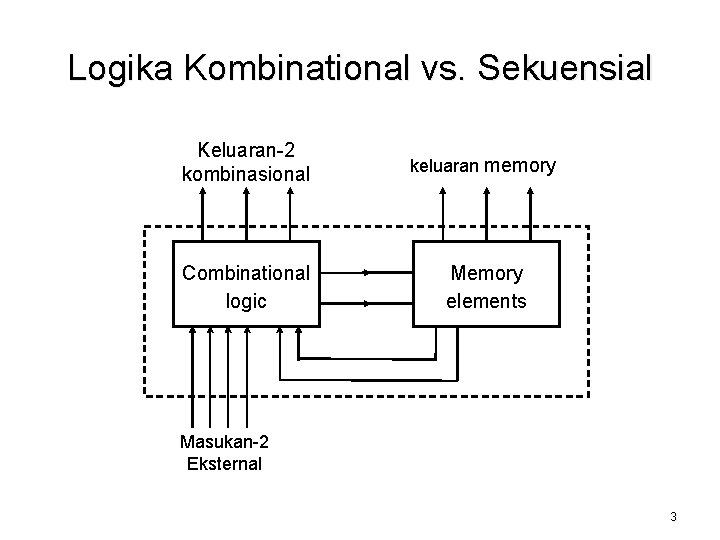
Logika Kombinational vs. Sekuensial Keluaran-2 kombinasional keluaran memory Combinational logic Memory elements Masukan-2 Eksternal 3

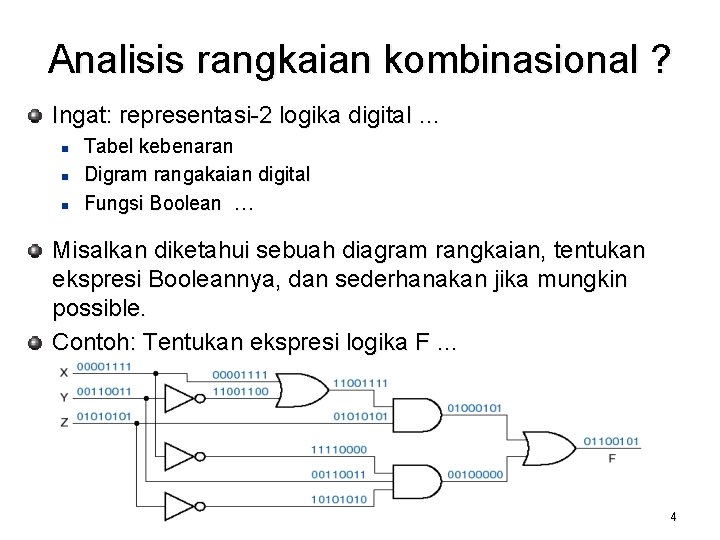
Analisis rangkaian kombinasional ? Ingat: representasi-2 logika digital … n n n Tabel kebenaran Digram rangakaian digital Fungsi Boolean … Misalkan diketahui sebuah diagram rangkaian, tentukan ekspresi Booleannya, dan sederhanakan jika mungkin possible. Contoh: Tentukan ekspresi logika F … 4

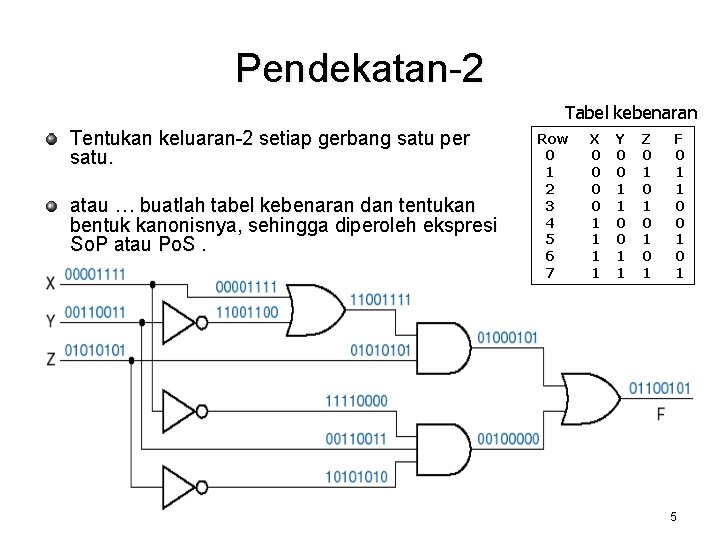
Pendekatan-2 Tabel kebenaran Tentukan keluaran-2 setiap gerbang satu per satu. atau … buatlah tabel kebenaran dan tentukan bentuk kanonisnya, sehingga diperoleh ekspresi So. P atau Po. S. Row 0 1 2 3 4 5 6 7 X 0 0 1 1 Y 0 0 1 1 Z 0 1 0 1 F 0 1 1 0 0 1 5

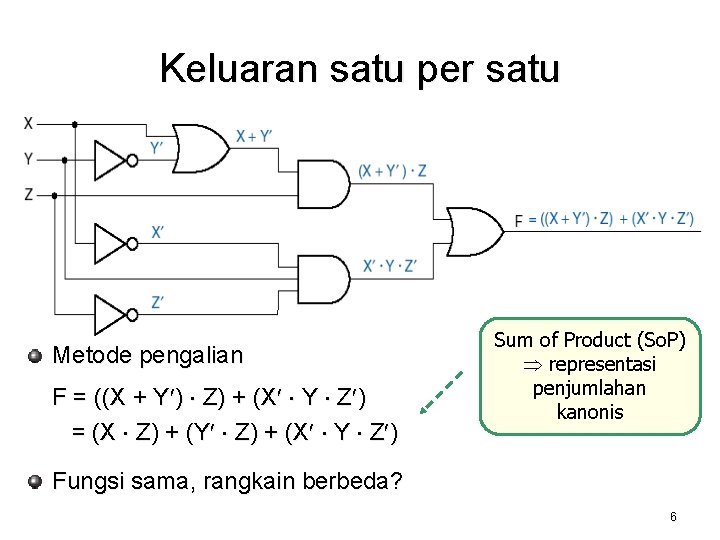
Keluaran satu per satu Metode pengalian F = ((X + Y¢) × Z) + (X¢ × Y × Z¢) = (X × Z) + (Y¢ × Z) + (X¢ × Y × Z¢) Sum of Product (So. P) representasi penjumlahan kanonis Fungsi sama, rangkain berbeda? 6

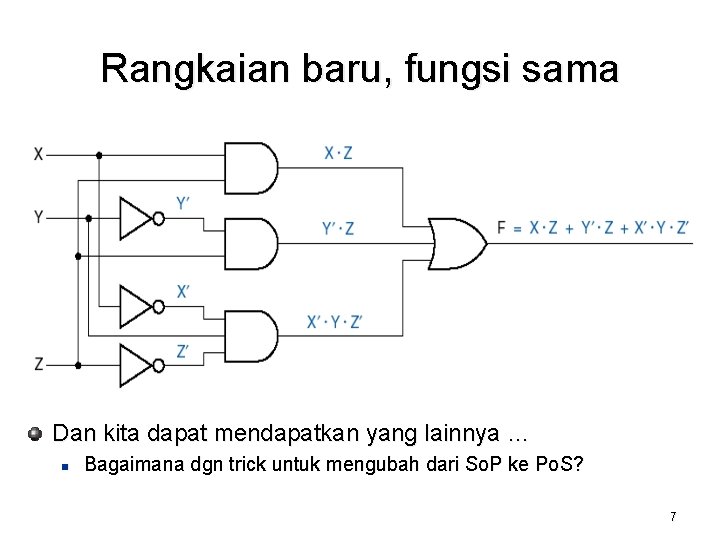
Rangkaian baru, fungsi sama Dan kita dapat mendapatkan yang lainnya … n Bagaimana dgn trick untuk mengubah dari So. P ke Po. S? 7

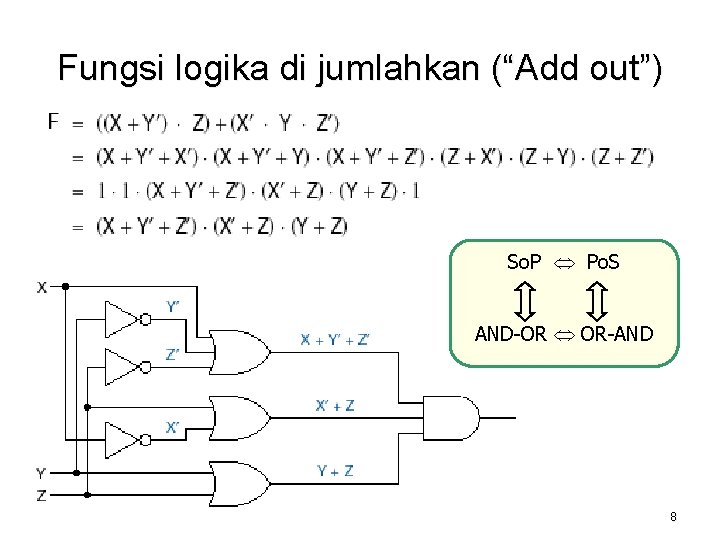
Fungsi logika di jumlahkan (“Add out”) So. P Po. S AND-OR OR-AND 8

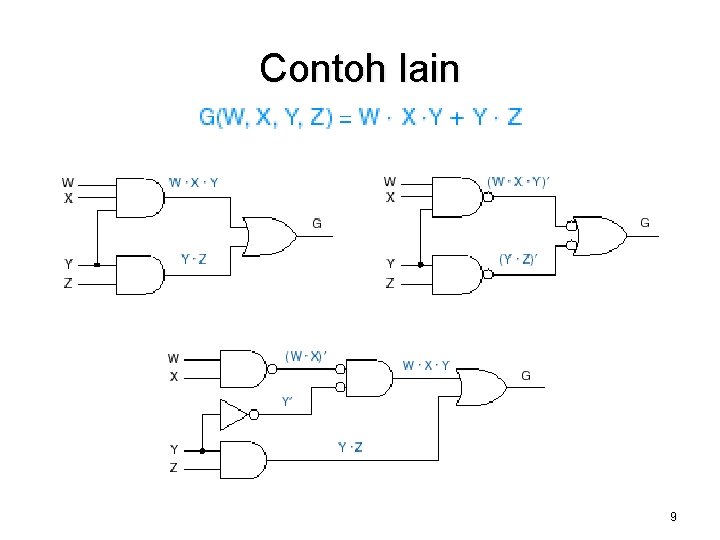
Contoh lain 9

Rangkaian mana yang lebih baik? So. P, Po. S, atau …? Ingat: level transistor (yaitu, TTL), NAND/NOR memiliki transistor lebih sedikit ketimbang AND/OR. Ingat: teorema De. Morgan n n Konversikan So. P ke NAND-NAND F=A·B+C·D = ((A · B)’)’ + ((C · D)’)’ (T 4) = ( (A · B)’ · (C · D)’ )’ (De. Morgan’s theorem T 13) Konversikan Po. S ke NOR-NOR F = (A + B) · (C + D) = ((A + B)’)’ · ((C + D)’)’ (T 4) = ( (A + B)’ + (C + D)’ )’ (De. Morgan’s theorem T 13’) 10

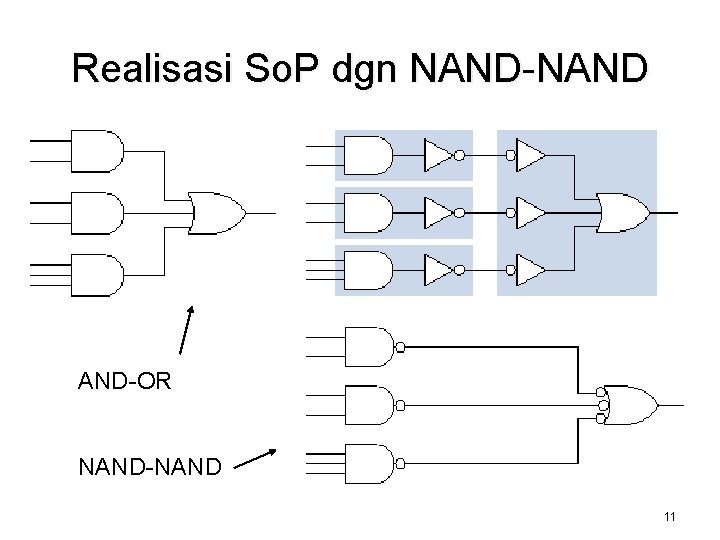
Realisasi So. P dgn NAND-NAND AND-OR NAND-NAND 11

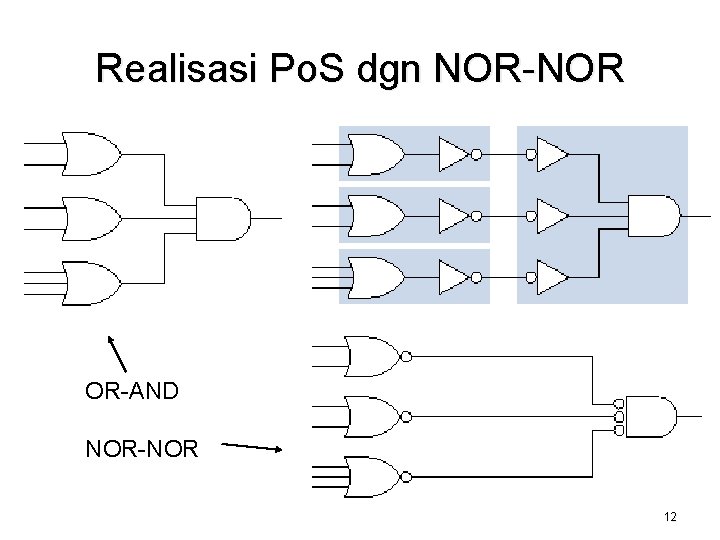
Realisasi Po. S dgn NOR-NOR OR-AND NOR-NOR 12

Ringkasan Menurunkan fungsi-2 Boolean dari rangkaian digital Menyederhanakan fungsi-2 Boolean dgn menggunakan teorema-2 aljabar switching n (T 10, T 10’), (T 13, T 13’) teorema De. Morgan, … Konstruksi rangkaian alternatif berbasis fungsi-2 Boolean yang disederhanakan n AND-OR, OR-AND, and others Konversi AND-OR ke NAND-NAND, dan OR-AND ke NOR-NOR 13