KUEL A JEHO POVRCH VY42INOVACE 3102 Rotan kuel

KUŽEL A JEHO POVRCH VY_42_INOVACE_ 31_02

Rotační kužel vznikne otáčením pravoúhlého trojúhelníku kolem přímky o, na které leží jedna jeho odvěsna. o obr. 1 obr. 2

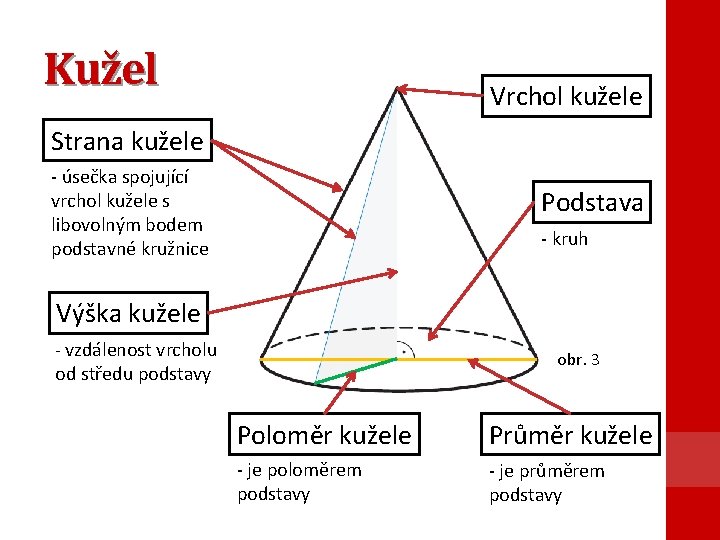
Kužel Vrchol kužele Strana kužele - úsečka spojující vrchol kužele s libovolným bodem podstavné kružnice Podstava - kruh Výška kužele - vzdálenost vrcholu obr. 3 od středu podstavy Poloměr kužele Průměr kužele - je poloměrem podstavy - je průměrem podstavy

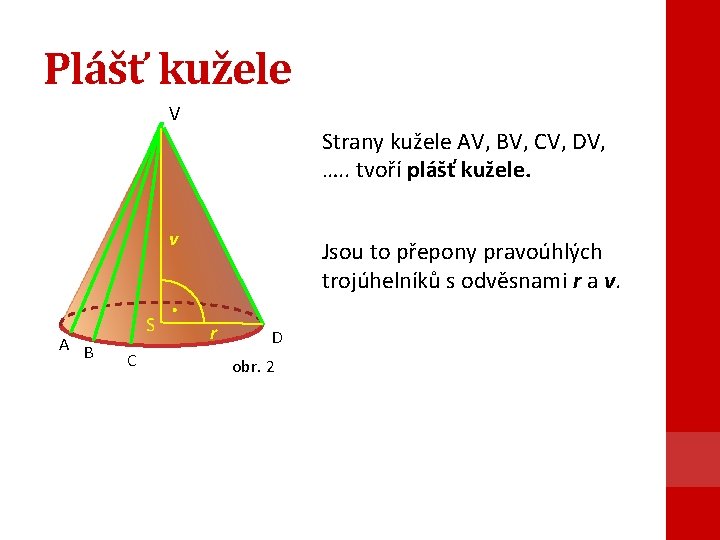
Plášť kužele V Strany kužele AV, BV, CV, DV, …. . tvoří plášť kužele. v A B S C Jsou to přepony pravoúhlých trojúhelníků s odvěsnami r a v. . r D obr. 2

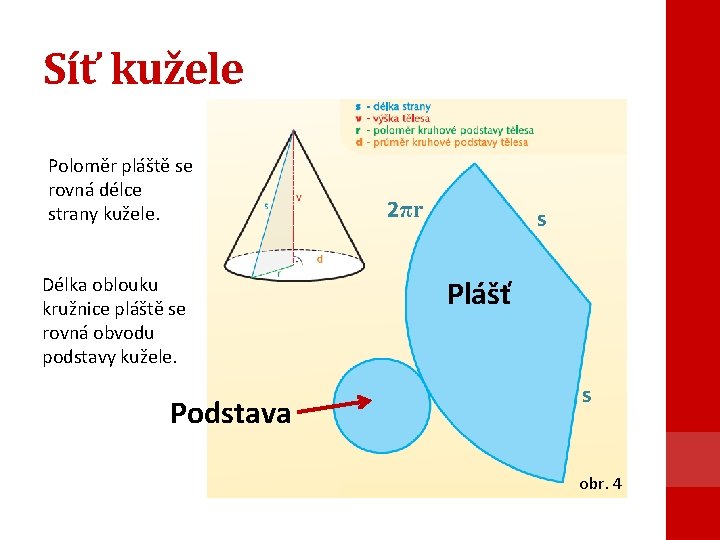
Síť kužele Poloměr pláště se rovná délce strany kužele. Délka oblouku kružnice pláště se rovná obvodu podstavy kužele. Podstava 2πr s Plášť s obr. 4

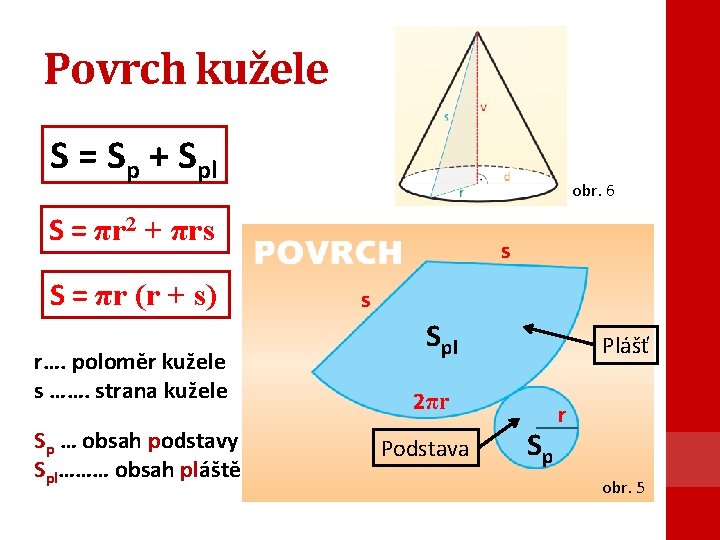
Povrch kužele S = Sp + Spl obr. 6 S = πr 2 + πrs S = πr (r + s) r…. poloměr kužele s ……. strana kužele Sp … obsah podstavy Spl……… obsah pláště s s Spl Plášť 2πr Podstava Sp r obr. 5

Příklad Vypočítej povrch kužele s poloměrem podstavy 3 cm a délkou strany 6 cm. Výsledek zaokrouhli na čtverečné centimetry. s = 6 cm S = πr (r + s) S = 3, 14. 3. (3 + 6) S = 84, 78 cm 2 r = 3 cm obr. 3

Příklad Vypočítej povrch kužele s poloměrem podstavy 3 cm a výškou 4 cm. Výsledek zaokrouhli na čtverečné centimetry. S = πr (r + s) S = 3, 14. 3. (3 + 5) S = 75, 36 cm 2 s=? v = 4 cm obr. 3 r = 3 cm s = ? s 2 = r 2 + v 2 s 2 = 32 + 42 s 2 = 9 + 16 s = 5 cm

Tato práce je šířena pod licencí CC BY-SA 3. 0. Odkazy a citace jsou platné k datu vytvoření této práce. Texty jsou vlastní originální tvorbou autora Citace: obr. 1 Všechny objekty použité k vytvoření tohoto obrázku jsou součástí softwaru Microsoft® Office. obr. 2 Kolmý rotační kužel. Datakabinet [online]. 2012 [cit. 2013 -04 -07]. Dostupné z: http: //www. datakabinet. cz/cs/Vyukove-materialy-a-data/Matematika-a-jeji-aplikace/Ilustrace-a -obrazky/Kolmy-rotacni-kuzel. html obr. 3 Kolmý rotační kužel bez popisu. Datakabinet [online]. 2012 [cit. 2013 -04 -07]. Dostupné z: http: //www. datakabinet. cz/cs/Vyukove-materialy-a-data/Matematika-a-jeji-aplikace/Ilustrace-a -obrazky/Kolmy-rotacni-kuzel-bez-popisu. html obr. 4, 5, 6 Povrchy a objemy těles. Datakabinet [online]. 2012 [cit. 2013 -04 -07]. Dostupné z: http: //www. datakabinet. cz/cs/Vyukove-materialy-a-data/Matematika-a-jeji-aplikace/Vyukovetabulky/Povrchy-a-objemy-teles. html

Škola: Základní škola Trávníky Otrokovice, příspěvková organizace Číslo projektu: CZ. 1. 07/1. 4. 00/21. 2637 Název výukového materiálu: Kužel a jeho povrch Autor: Mgr. Miroslava Málková Vytvořeno: 7. dubna 2013 Ročník: 9. Vzdělávací oblast: Matematika a její aplikace Vzdělávací obor: Matematika a její aplikace Tematický okruh: Geometrie v rovině a v prostoru Téma: Kužel Pomůcky: notebook, dataprojektor, sešit, psací potřeby, výukové tabulky a materiály Datakabinetu Anotace: Vzdělávací materiál je určen k výkladu učiva o kuželu. Obsahuje popis tělesa a jeho síť. Je zde uveden vzorec k výpočtu povrchu kužele. Materiál je doplněn příkladem výpočtu povrchu kužele.