Kuantum Mekanii MSGS Felsefe Blm 4 Mays 2011

Kuantum Mekaniği MSGSÜ Felsefe Bölümü 4 Mayıs 2011 Cemsinan Deliduman

Max Planck

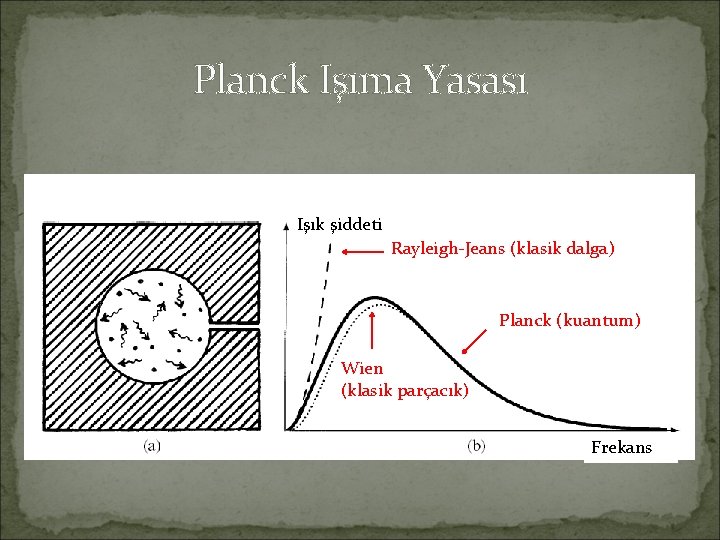
Planck Işıma Yasası Işık şiddeti Rayleigh-Jeans (klasik dalga) Planck (kuantum) Wien (klasik parçacık) Frekans

Albert Einstein

Einstein ve Fotoelektrik Etkisi Fotonlar Yüzeyden fırlatılan elektronlar Sodyum Metali

Klasik Atom Modelinin Sorunları �Elektronlar atom çekirdeğinin etrafında gezegenler gibi dönüyorlarsa, ışıma yapıp çekirdeğe düşmelerini engelleyen nedir?

Niels Bohr

Bohr Atom Modeli 2 s yörüngesi Atom çekirdeği 2 p yörüngeleri 1 s yörüngesi 3 s yörüngesi

Elektron Yörüngeleri 422 531 �Elektronlar atom çekirdeği etrafında klasik fizik ile öngörülemeyecek yörüngelerde bulunuyorlar.

Parçacık-Dalga İkiliği

Klasik Parçacıklarla Çift Yarık Deneyi

Dalgalarla Çift Yarık Deneyi

Girişim Deseni ışık dalgaları çift yarık girişim deseni

Elektronlarla Çift Yarık Deneyi

Parçacık mı, Dalga mı? Elektronların hangi yarıktan geçtikleri gözlemlenirse Elektronların hangi yarıktan geçtikleri gözlemlenmezse

Fotonlarla Çift Yarık Deneyi �Fotonlar çift yarık deneyinde tıpkı elektronlar gibi davranırlar. �Elektron da ışık gibi bir tür dalga olmalıdır.

Dalga Fonksiyonu q Parçacık olarak bilinen herşey bir dalga fonksiyonuna sahiptir. ß Konum değişkenine göre dalga fonksiyonu Momentum değişkenine göre dalga fonksiyonu.

Kuantum Mekaniğinde Ölçme Problemi gözlemden önce foton elektron gözlemci gözlemden sonra gözlem elektronun konumunu ve momentumunu etkiler

Heisenberg Belirsizlik İlkesi �Bir parçacığın hem konumu hem de momentumu aynı anda mutlak kesinlikle ölçülemez. �Konumu mutlak kesinlikle ölçülürse momentumu hakkında (veya tam tersi) hiçbir şey bilinemez.

Kuantum Tünelleme Klasik fizik elektron Kuantum fiziği elektron dalgası engel

Kuantum Durumları

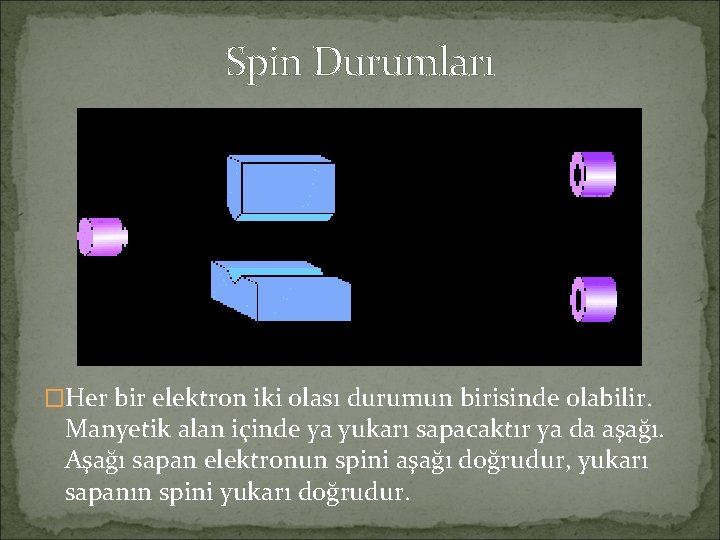
Spin Durumları �Her bir elektron iki olası durumun birisinde olabilir. Manyetik alan içinde ya yukarı sapacaktır ya da aşağı. Aşağı sapan elektronun spini aşağı doğrudur, yukarı sapanın spini yukarı doğrudur.

Riemann Durumlar Kümesi �Ölçümden önce elektron spin durumlarının herhangi birinde veya bu durumların bir bileşiminde olabilir. Bu farklı bileşimlerin kümesine Riemann durumlar kümesi denir.

Dalga Paketi �Dalga paketi farklı dalga boyu olan birçok dalganın birleşmesiyle oluşur.

Hilbert Uzayı �Hilbert uzayı olası tüm kuantum durumlarının veya dalga fonksiyonlarının her birinin ayrı bir vektörle temsil edildiği bir temsil uzayıdır.

Ölçüm �Ölçüm sonucaunda dalga paketi kendisini oluşturan dalgalardan birine çöker.

U ve R Evrimleri �Dalga fonksiyonu iki şekilde evrimleşir: Ø U-evrimi: Dalga fonksiyonu Schrödinger dalga denklemiyle verilen zaman bağımlılığına uygun şekilde evrilir.

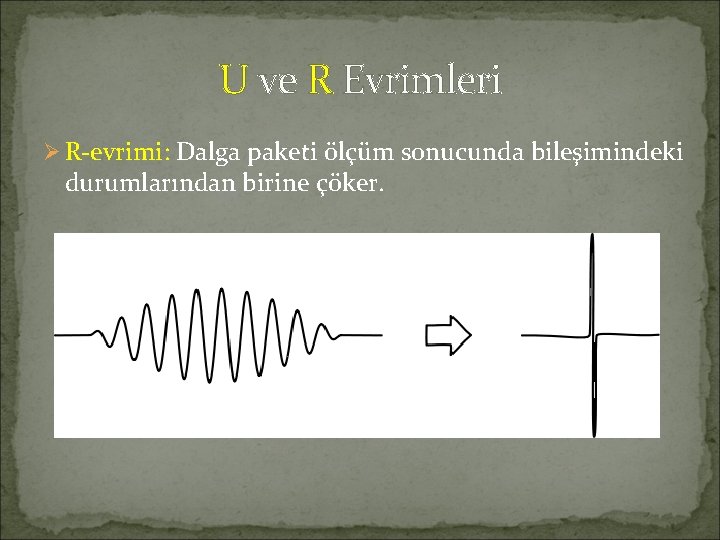
U ve R Evrimleri Ø R-evrimi: Dalga paketi ölçüm sonucunda bileşimindeki durumlarından birine çöker.

Kuantum Durumlarının Nesnelliği? � Bir parçacığın konumunu ölçüyor olalım ve ölçümden sonra parçacığın konumunu belirleyelim. � Ölçmeden önce parçacık nerededir? Ölçümden sonra bulduğumuz yerde. b) Her yerdedir. Sistem parçacığın hangi olasılıkla nerede olduğunu “bilir”. c) Hiç bir yerde değildir. Ölçüm parçacığı belli bir yerde olmaya zorlar. d) Ölçmeden parçacığın nerede olduğunu bilemeyiz. a)

Kuantum Durumlarının Nesnelliği? � Bir parçacığın konumunu ölçüyor olalım ve ölçümden sonra parçacığın konumunu belirleyelim. � Ölçmeden önce parçacık nerededir? Ölçümden sonra bulduğumuz yerde. b) Her yerdedir. Sistem parçacığın hangi olasılıkla nerede olduğunu “bilir”. c) Hiç bir yerde değildir. Ölçüm parçacığı belli bir yerde olmaya zorlar. d) Ölçmeden parçacığın nerede olduğunu bilemeyiz. a) Ø Doğru cevap: (c) seçeneği.

Schrödinger’in Kedisi

Schrödinger’in Kedisi

Radyoaktif Bozunma Atomun U-evrimi

Sistemin Kuantum Durumları Kedinin U-evrimi

Kedinin Durumu? �Ölçmeden önce kedi canlı mıdır, ölü müdür? a) Ölçümden sonra nasıl bulduysak öyledir. b) Hem canlıdır, hem ölüdür. Sistem kedinin hangi olasılıkla ne durumda olduğunu “bilir”. c) Hiçbir şey değildir. Ölçüm kediyi belli bir durumda olmaya zorlar. d) Ölçmeden kedinin durumunu bilemeyiz. Ø Doğru cevap (c) seçeneği mi?

Schrödinger’in Kedisi

Dalga Fonksiyonunun Anlamı? �Dalga fonksiyonunun bir gerçekliği var mıdır? �Eğer bir gerçekliği var ise sadece dalga fonksiyonu kullanarak klasik fizikle bağlantı kurulabilir mi? �Kuantum mekaniğinin dalga fonksiyonunu temel alan bir yorumu olabilir mi? Yoksa dalga fonksiyonu daha geniş bir kuantum kuramında mı anlam kazanacaktır? �Eğer dalga fonksiyonunun bir gerçekliği yoksa ve sadece gözlemcinin kafasındaysa, öznel midir?

Kuantum Fiziğinin Everett Yorumu

Kuantum Mekaniği ve Belirlenimcilik �U-evrimi bize belirlenimci bir kuram portresi çiziyor: Schrödinger denkleminin çözümü dalga fonksiyonunun zaman bağımlılığını verir. �R-evrimi ölçme sırasında gerçekleşir ve belirlenimci değildir. �Dalga fonksiyonun karesinin alınarak olasılıklar hesaplanması belirlenimci bir fizik vermiyor. Ø Kuantum kuramı belirlenimcidir, ancak klasik fizikle bağlantı kurma yöntemimiz belirlenimci değildir.

Anahtar Kelimeler Planck Işıma yasası Fotoelektrik etkisi Bohr atom modeli Çift yarık deneyi Parçacık-Dalga ikiliği Dalga Fonksiyonu Ölçme problemi Kuantum tünelleme Heisenberg belirsizlik ilkesi Spin durumları Dalga paketi Hilbert uzayı U ve R evrimleri Schrödinger’in kedisi Everett yorumu