KS 4 Mathematics A 2 Linear equations 1

KS 4 Mathematics A 2 Linear equations 1 of 29 © Boardworks Ltd 2005

Contents A 2 Linear equations A A 2. 1 Equations, formulae and identities A A 2. 2 Balancing equations A A 2. 3 Equations with brackets A A 2. 4 Equations with fractions A A 2. 5 Using equations to solve problems 2 of 29 © Boardworks Ltd 2005

Expressions and identities Remember in an algebraic expression we usually have a combination of numbers, letters and operations. For example, 3 x + 5 + 2 x – 6. Expressions do not contain an equals sign. Sometimes an expression is rewritten in an equivalent form. 3 x + 5 + 2 x – 6 = 5 x – 1 This is an example of an identity. An identity is true for all values of x. This is sometimes written with the symbol ≡ as, 3 x + 5 + 2 x – 6 ≡ 5 x – 1 Is identically equal to 3 of 29 © Boardworks Ltd 2005

Equations An equation links an algebraic expression and a number, or two algebraic expressions with an equals sign. For example, x + 7 = 13 is an equation. In an equation the unknown usually has a particular value. Finding the value of the unknown is called solving the equation. x + 7 = 13 x=6 When we solve an equation we should line up the equals signs. 4 of 29 © Boardworks Ltd 2005

Formulae A formula is a special type of equation that links two or more physical variables. For example in the formula, P = 2(l + w) P represents the perimeter of a rectangle and l and w represent its length and width. We can use this formula to work out the perimeter of any rectangle given its length and width. Physical variables such as length, time, mass and temperature have units attached to them. These are not written in the formula and so it is important that they are consistent. 5 of 29 © Boardworks Ltd 2005

Contents A 2 Linear equations A A 2. 1 Equations, formulae and identities A A 2. 2 Balancing equations A A 2. 3 Equations with brackets A A 2. 4 Equations with fractions A A 2. 5 Using equations to solve problems 6 of 29 © Boardworks Ltd 2005

Linear equations are the easiest type of equation to solve because the unknown is not raised to any power other than 1. We can solve very simple linear equations by inspection. For example, 19 – x = 8 x = 11 7 x = 42 x=6 7 of 29 We think of this as, “what number subtracted from 19 gives us an answer of 8? ” We think of this as, “what number multiplied by 7 gives us an answer of 42? ” © Boardworks Ltd 2005

Linear equations When more than one operation is preformed on the unknown we need to solve the equation in several steps. We can do this by performing the same operations to both sides of the equals sign to keep the equation balanced. For example, 4 x + 5 = 29 – 5 subtract 5 from both sides: 4 x = 24 ÷ 4 divide both sides by 4: – 5 ÷ 4 x=6 Check that 4 × 6 + 5 is equal to 29 in the original equation. 8 of 29 © Boardworks Ltd 2005

Equations with unknowns on both sides In some cases the unknown appears on both sides of the equals sign. For this type of equation it is important to work systematically to collect terms with unknowns on the left hand side of the equation and numbers on the right. Always aim to have a single unknown on the left equal to a single number on the right. For example, unknowns numbers 6 x – 2 = 2 x + 1 Here we’ll label the sides as ‘unknowns’ and ‘numbers’. We are aiming to have the unknown on the left and a number on the right. 9 of 29 © Boardworks Ltd 2005

Equations with unknown on both sides The equation can then be solved by performing the same operations on both sides until the solution is found. unknowns numbers 8 x – 2 = 2 x + 1 add 2 to both sides: +2 +2 8 x = 2 x + 3 subtract 2 x from both sides: – 2 x 6 x = 3 divide both sides by 6: ÷ 6 x = 0. 5 Check by substituting x = 0. 5 into the expressions in the original equation. Both sides are equal to 2, so the solution is correct. 10 of 29 © Boardworks Ltd 2005

Contents A 2 Linear equations A A 2. 1 Equations, formulae and identities A A 2. 2 Balancing equations A A 2. 3 Equations with brackets A A 2. 4 Equations with fractions A A 2. 5 Using equations to solve problems 11 of 29 © Boardworks Ltd 2005

Equations with brackets Equations can contain brackets. For example, 2(3 x – 5) = 4 x To solve this we can multiply out the brackets: 6 x – 10 = 4 x + 10 add 10 to both sides: + 10 6 x = 4 x + 10 - 4 x subtract 4 x from both sides: 2 x = 10 ÷ 2 divide both sides by 2: 12 of 29 ÷ 2 x=5 © Boardworks Ltd 2005

Equations with brackets Sometimes we can solve equations such as 2(3 x – 5) = 4 x by first dividing both sides by the number in front of the bracket: divide both sides by 2: 3 x – 5 = 2 x +5 add 5 to both sides: +5 3 x = 2 x + 5 - 2 x subtract 2 x from both sides: x=5 In this example, dividing first means that there are fewer steps. 13 of 29 © Boardworks Ltd 2005

Contents A 2 Linear equations A A 2. 1 Equations, formulae and identities A A 2. 2 Balancing equations A A 2. 3 Equations with brackets A A 2. 4 Equations with fractions A A 2. 5 Using equations to solve problems 14 of 29 © Boardworks Ltd 2005

Solving equations with fractional coefficients Sometimes the coefficient of an unknown is a fraction. For example, 3 4 x– 5=9–x We can remove the 4 from the denominator by multiplying both sides of the equation by 4. 4( 3 4 x – 5) = 4(9 – x) expand the brackets: 3 x – 20 = 36 – 4 x add 4 x to both sides: 7 x – 20 = 36 add 20 to both sides: 7 x = 56 divide both sides by 7: 15 of 29 x=8 © Boardworks Ltd 2005

Solving equations with fractional coefficients If an equation contains more than one fraction, these can be removed by multiplying throughout by the lowest common multiple of the two denominators. For example, 2 3 1 x= 2 x+1 What is the lowest common multiple of 3 and 2? The lowest common multiple of 3 and 2 is 6. Multiplying both sides by 6, 2 1 6( 3 x) = 6( 2 x + 1) expand the brackets: subtracting 3 x from both sides: 16 of 29 4 x = 3 x + 6 x=6 © Boardworks Ltd 2005

Solving equations involving division In this example the whole of one side of the equation is divided by 5. 2 x + 7 =x– 1 5 To remove the 5 from the denominator we multiply both sides of the equation by 5. 2 x + 7 = 5(x – 1) expand the brackets: 2 x + 7 = 5 x – 5 swap sides: 5 x – 5 = 2 x + 7 add 5 to both sides: 5 x = 2 x + 12 subtract 2 x from both sides: 3 x = 12 divide both sides by 3: x=4 17 of 29 © Boardworks Ltd 2005

Solving equations involving division When both sides of an equation are divided by a number we must remove these by multiplying both sides by the lowest common multiple of the two denominators. For example, 5 x – 3 2 x – 1 = 4 3 What is the lowest common multiple of 4 and 3? The lowest common multiple of 4 and 3 is 12. Multiplying every term by 12 gives us: 3 4 12(5 x – 3) 12(2 x – 1) = 41 31 which simplifies to: 3(5 x – 3) = 4(2 x – 1) 18 of 29 © Boardworks Ltd 2005

Solving equations involving division We can then solve the equation as usual. 3(5 x – 3) = 4(2 x – 1) expand the brackets: add 9 to both sides: 15 x – 9 = 8 x – 4 15 x = 8 x + 5 subtract 8 x from both sides: 7 x = 5 divide both sides by 7: x= 5 7 Although this answer could be written as a rounded decimal, it is more exact left as a fraction. 19 of 29 © Boardworks Ltd 2005

Solving equations involving division We have seen that simplifies to 5 x – 3 2 x – 1 = 3 4 3(5 x – 3) = 4(2 x – 1) How could we perform this simplification in one step? Multiplying both sides by 4 cancels out the 4 on the left hand side and multiplies the expression on the right-hand side by 4. Multiplying both sides by 3 cancels out the 3 on the right hand side and multiplies the expression on the left-hand side by 3. Doing this in one step in often called cross-multiplication. 20 of 29 © Boardworks Ltd 2005

Simplifying equations by cross-multiplication 21 of 29 © Boardworks Ltd 2005

Solving equations involving division Sometimes the unknowns appear in the denominator. For example, 4 5 = (x + 3) (3 x – 5) In this example, we can multiply both sides by (x + 3) and (3 x – 5) in one step to give: 4(3 x – 5) = 5(x + 3) expand the brackets: subtract 5 x from both sides: add 20 to both sides: divide both sides by 7: 22 of 29 12 x – 20 = 5 x + 15 7 x – 20 = 15 7 x = 35 x=5 © Boardworks Ltd 2005

Equivalent equations 23 of 29 © Boardworks Ltd 2005

Contents A 2 Linear equations A A 2. 1 Equations, formulae and identities A A 2. 2 Balancing equations A A 2. 3 Equations with brackets A A 2. 4 Equations with fractions A A 2. 5 Using equations to solve problems 24 of 29 © Boardworks Ltd 2005

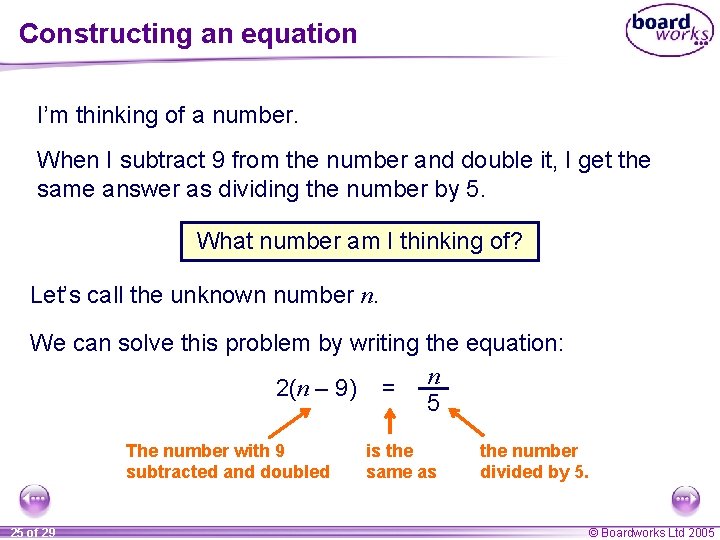
Constructing an equation I’m thinking of a number. When I subtract 9 from the number and double it, I get the same answer as dividing the number by 5. What number am I thinking of? Let’s call the unknown number n. We can solve this problem by writing the equation: n 2(n – 9) = 5 The number with 9 subtracted and doubled 25 of 29 is the same as the number divided by 5. © Boardworks Ltd 2005

Solving the equation We can solve this equation by performing the same operations on both sides, n 2(n – 9) = 5 multiply both side by 5: 10(n – 9) = n expand the bracket: add 90 to both sides: subtract n from both sides: divide both sides by 9: 10 n – 90 = n 10 n = n + 90 9 n = 90 n = 10 We can check the solution by substituting it back into the original equation: 2 × (10 – 9) = 10 ÷ 5 26 of 29 © Boardworks Ltd 2005

Using equations to solve problems The sum of the ages of Ben and his daughter, Alice, is 66 years. In one year’s time Ben will be three times Alice’s age. How old is Alice now? Let’s call Alice’s age a. Looking at the first piece of information we can write Ben’s current age as 66 – a. Using the second piece of information we can also write Ben’s current age as 3(a + 1) – 1 This is three times Alice’s age in one year time, minus one to give Ben’s age now. This simplifies to, 3(a + 1) – 1 = 3 a + 3 – 1 = 3 a + 2 27 of 29 © Boardworks Ltd 2005

Using equations to solve problems The expressions 66 – a and 3 a + 2 both give Ben’s current age. This means that they are equal and so we can write them in an equation: 66 – a = 3 a + 2 swap sides: 3 a + 2 = 66 – a subtract 2 from each side: 3 a = 64 – a add a to both sides: 4 a = 64 divide both sides by 4: a = 16 Alice is 16, so Ben is 50. In one year Alice will be 17 and Ben will be 51. 51 is three times 17, so our solution is correct. 28 of 29 © Boardworks Ltd 2005

Find the value of x 29 of 29 © Boardworks Ltd 2005