KS 3 Mathematics S 1 Lines and Angles

KS 3 Mathematics S 1 Lines and Angles 1 of 69 © Boardworks Ltd 2004

Contents S 1 Lines and angles S 1. 1 Labelling lines and angles S 1. 2 Parallel and perpendicular lines S 1. 3 Calculating angles S 1. 4 Angles in polygons 2 of 69 © Boardworks Ltd 2004

Lines In Mathematics, a straight line is defined as having infinite length and no width. Is this possible in real life? 3 of 69 © Boardworks Ltd 2004

Labelling line segments When a line has end points we say that it has finite length. It is called a line segment. We usually label the end points with capital letters. For example, this line segment A B has end points A and B. We can call this line, line segment AB. 4 of 69 © Boardworks Ltd 2004

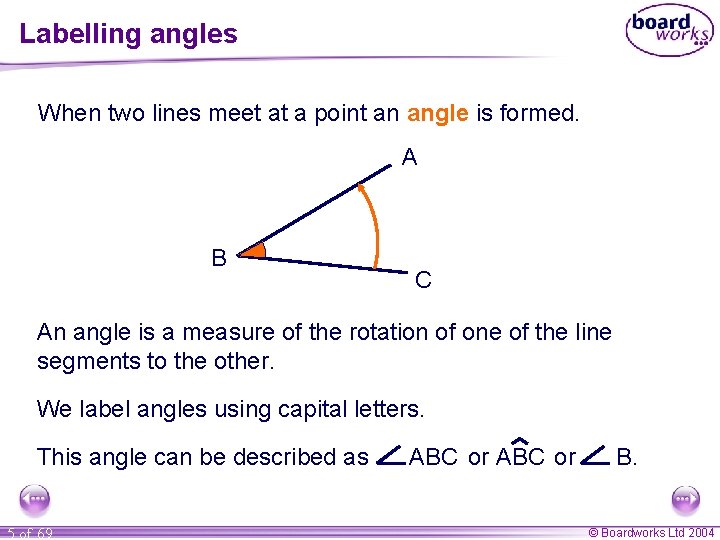
Labelling angles When two lines meet at a point an angle is formed. A B C An angle is a measure of the rotation of one of the line segments to the other. We label angles using capital letters. This angle can be described as 5 of 69 ABC or B. © Boardworks Ltd 2004

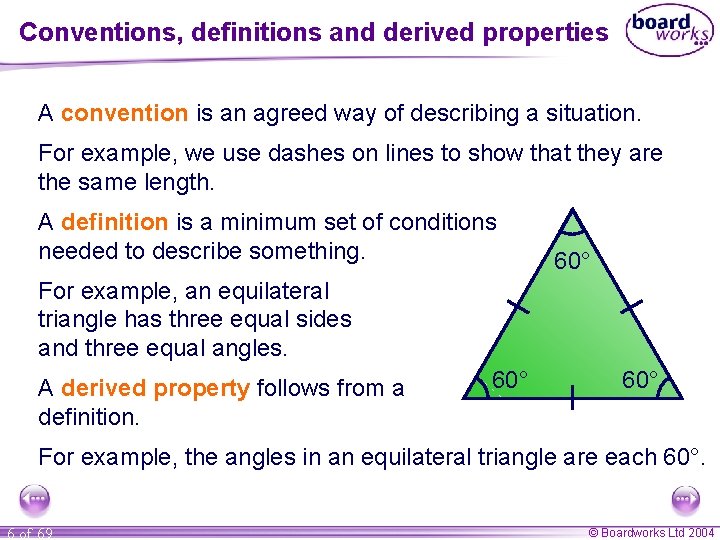
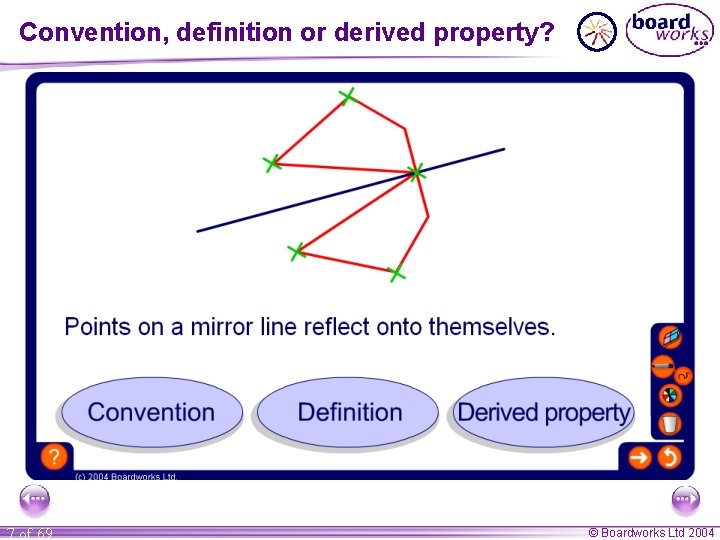
Conventions, definitions and derived properties A convention is an agreed way of describing a situation. For example, we use dashes on lines to show that they are the same length. A definition is a minimum set of conditions needed to describe something. 60° For example, an equilateral triangle has three equal sides and three equal angles. A derived property follows from a definition. 60° For example, the angles in an equilateral triangle are each 60°. 6 of 69 © Boardworks Ltd 2004

Convention, definition or derived property? 7 of 69 © Boardworks Ltd 2004

Contents S 1 Lines and angles S 1. 1 Labelling lines and angles S 1. 2 Parallel and perpendicular lines S 1. 3 Calculating angles S 1. 4 Angles in polygons 8 of 69 © Boardworks Ltd 2004

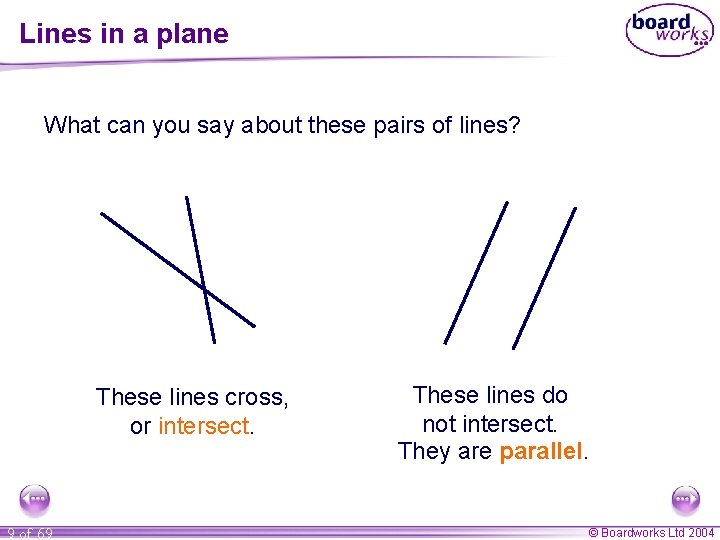
Lines in a plane What can you say about these pairs of lines? These lines cross, or intersect. 9 of 69 These lines do not intersect. They are parallel. © Boardworks Ltd 2004

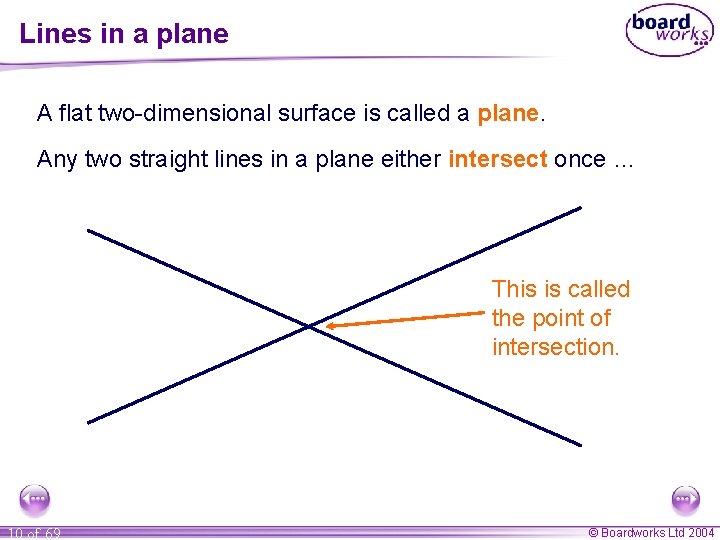
Lines in a plane A flat two-dimensional surface is called a plane. Any two straight lines in a plane either intersect once … This is called the point of intersection. 10 of 69 © Boardworks Ltd 2004

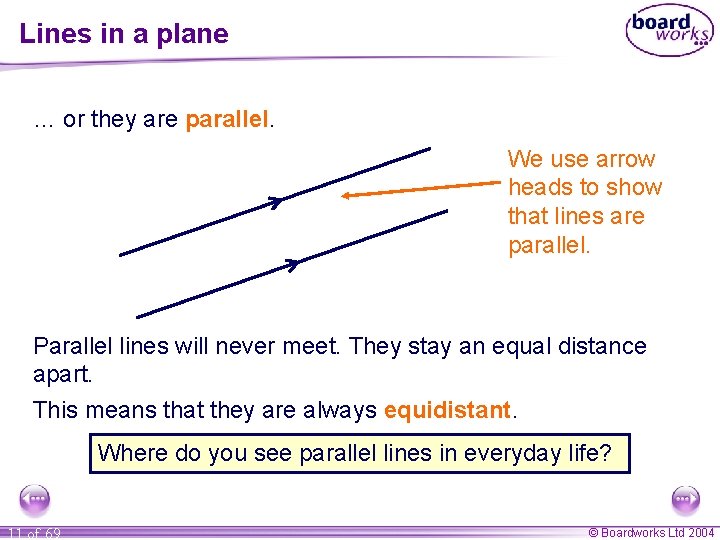
Lines in a plane … or they are parallel. We use arrow heads to show that lines are parallel. Parallel lines will never meet. They stay an equal distance apart. This means that they are always equidistant. Where do you see parallel lines in everyday life? 11 of 69 © Boardworks Ltd 2004

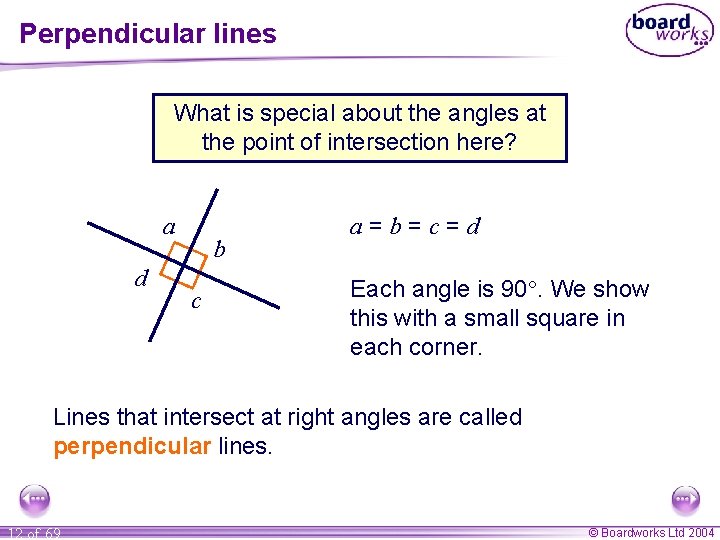
Perpendicular lines What is special about the angles at the point of intersection here? a d b c a=b=c=d Each angle is 90. We show this with a small square in each corner. Lines that intersect at right angles are called perpendicular lines. 12 of 69 © Boardworks Ltd 2004

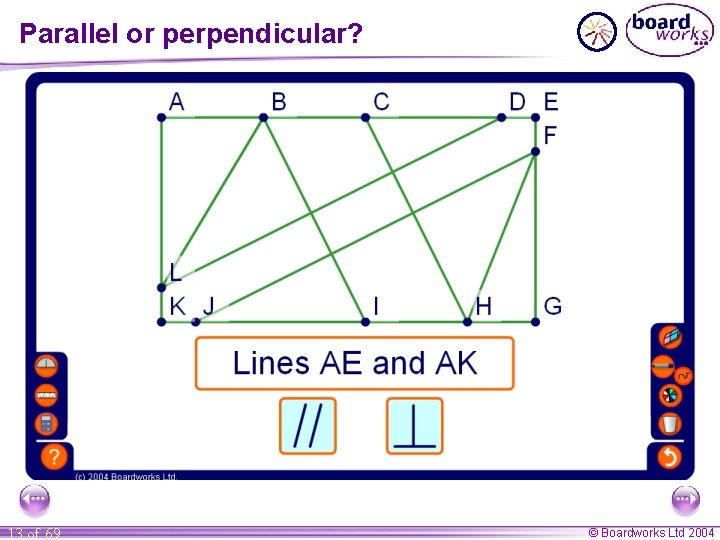
Parallel or perpendicular? 13 of 69 © Boardworks Ltd 2004

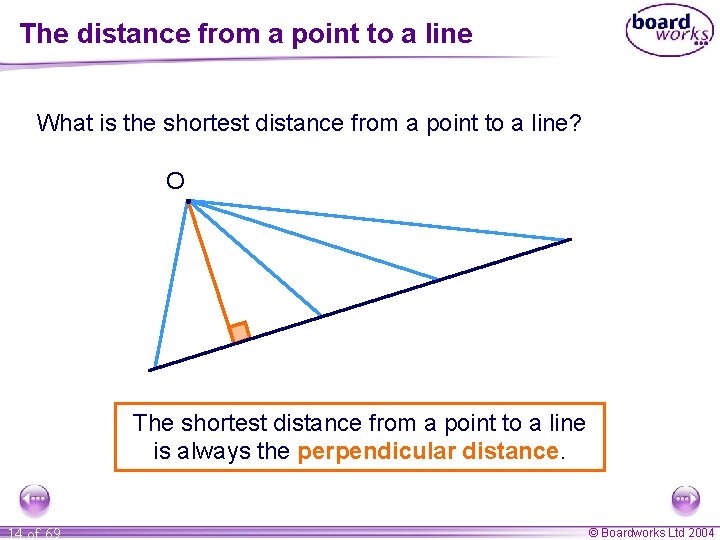
The distance from a point to a line What is the shortest distance from a point to a line? O The shortest distance from a point to a line is always the perpendicular distance. 14 of 69 © Boardworks Ltd 2004

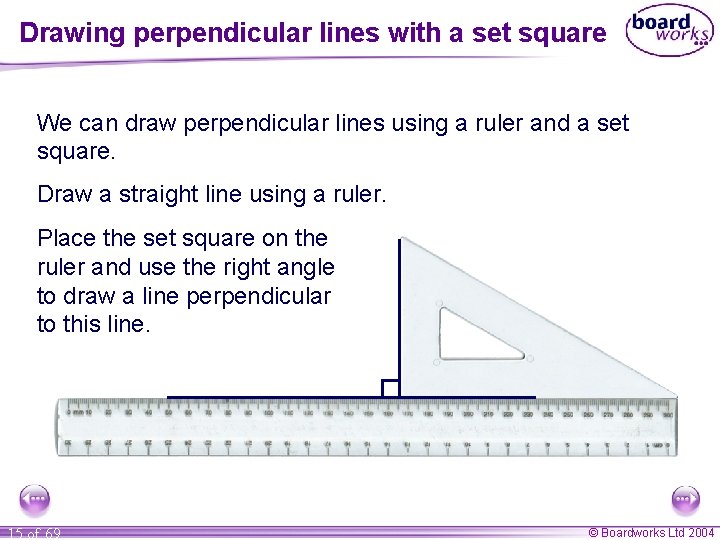
Drawing perpendicular lines with a set square We can draw perpendicular lines using a ruler and a set square. Draw a straight line using a ruler. Place the set square on the ruler and use the right angle to draw a line perpendicular to this line. 15 of 69 © Boardworks Ltd 2004

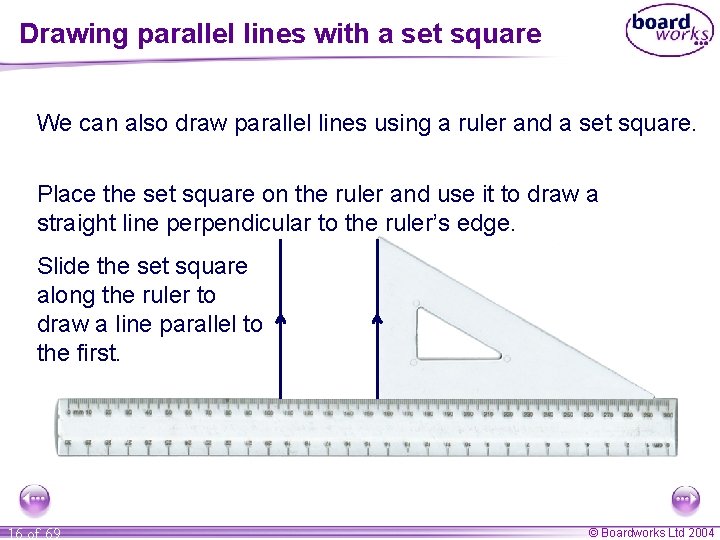
Drawing parallel lines with a set square We can also draw parallel lines using a ruler and a set square. Place the set square on the ruler and use it to draw a straight line perpendicular to the ruler’s edge. Slide the set square along the ruler to draw a line parallel to the first. 16 of 69 © Boardworks Ltd 2004

Contents S 1 Lines and angles S 1. 1 Labelling lines and angles S 1. 2 Parallel and perpendicular lines S 1. 3 Calculating angles S 1. 4 Angles in polygons 17 of 69 © Boardworks Ltd 2004

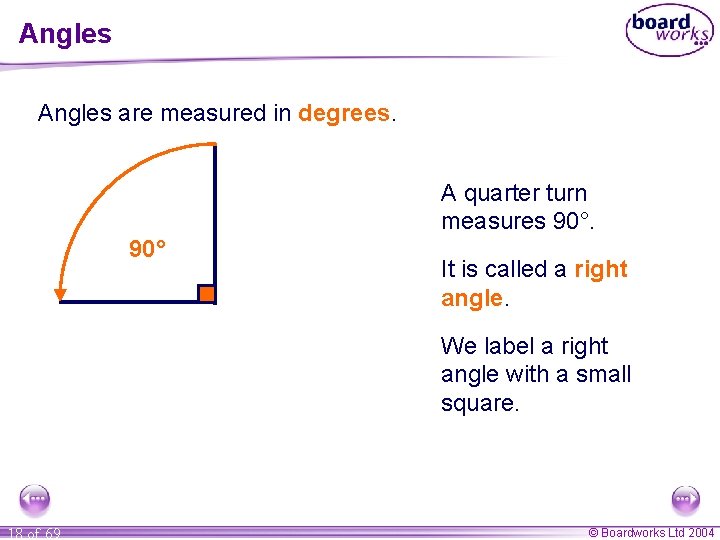
Angles are measured in degrees. A quarter turn measures 90° It is called a right angle. We label a right angle with a small square. 18 of 69 © Boardworks Ltd 2004

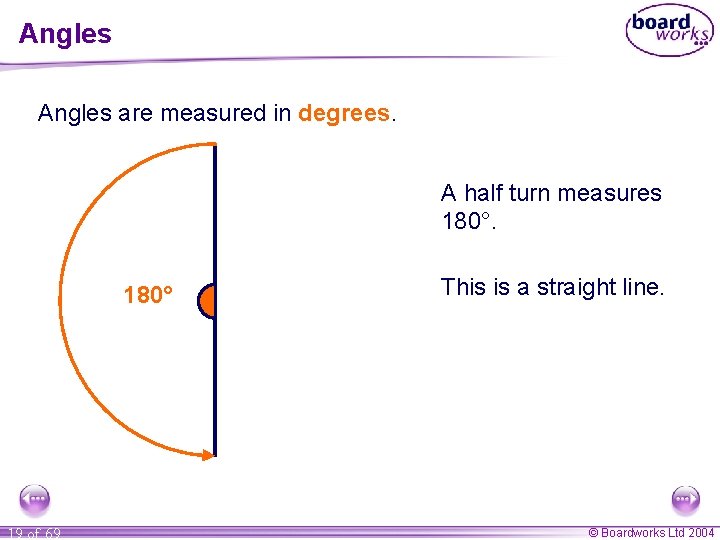
Angles are measured in degrees. A half turn measures 180° 19 of 69 This is a straight line. © Boardworks Ltd 2004

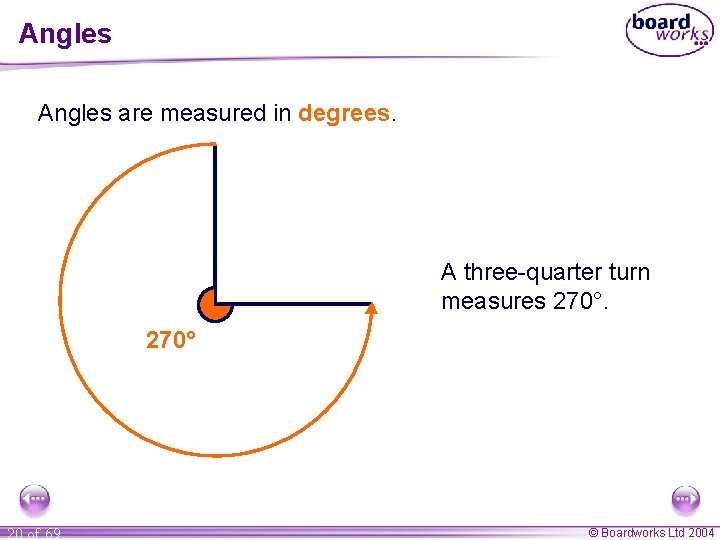
Angles are measured in degrees. A three-quarter turn measures 270° 20 of 69 © Boardworks Ltd 2004

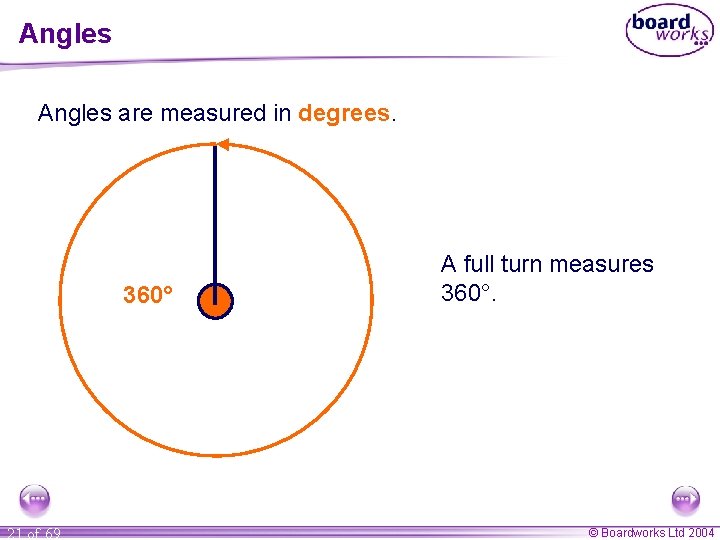
Angles are measured in degrees. 360° 21 of 69 A full turn measures 360°. © Boardworks Ltd 2004

Intersecting lines 22 of 69 © Boardworks Ltd 2004

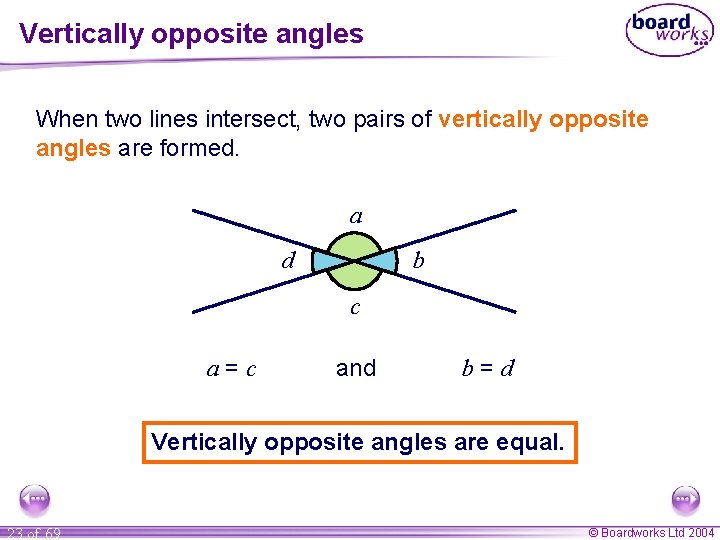
Vertically opposite angles When two lines intersect, two pairs of vertically opposite angles are formed. a d b c a=c and b=d Vertically opposite angles are equal. 23 of 69 © Boardworks Ltd 2004

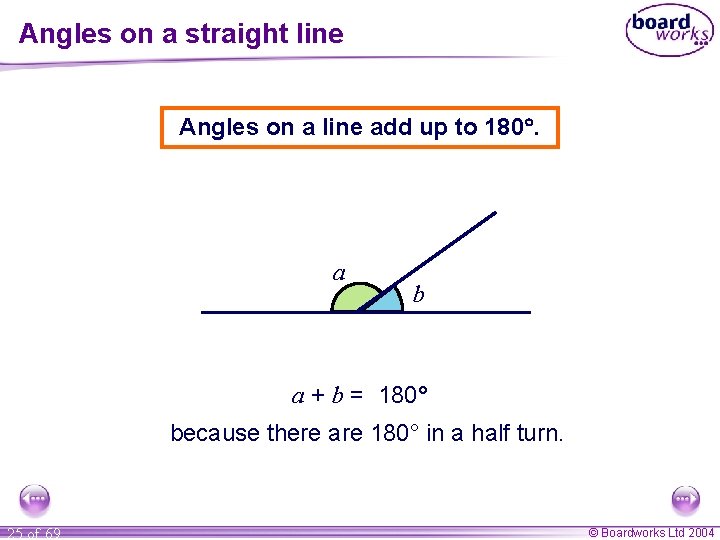
Angles on a straight line 24 of 69 © Boardworks Ltd 2004

Angles on a straight line Angles on a line add up to 180. a b a + b = 180° because there are 180° in a half turn. 25 of 69 © Boardworks Ltd 2004

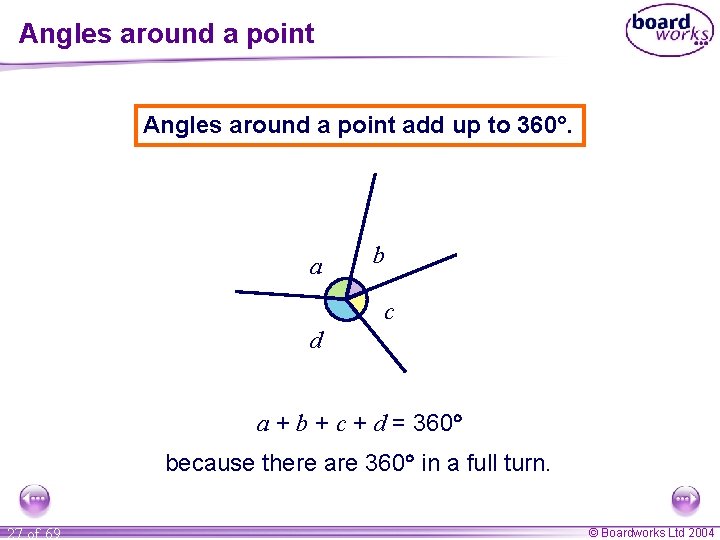
Angles around a point 26 of 69 © Boardworks Ltd 2004

Angles around a point add up to 360. a b c d a + b + c + d = 360 because there are 360 in a full turn. 27 of 69 © Boardworks Ltd 2004

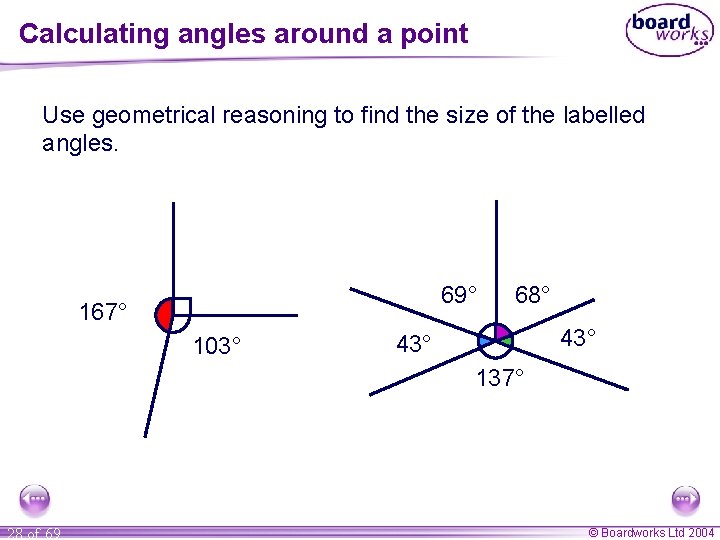
Calculating angles around a point Use geometrical reasoning to find the size of the labelled angles. 69° a 167° 103° d 68° c 43° b 43° 137° 28 of 69 © Boardworks Ltd 2004

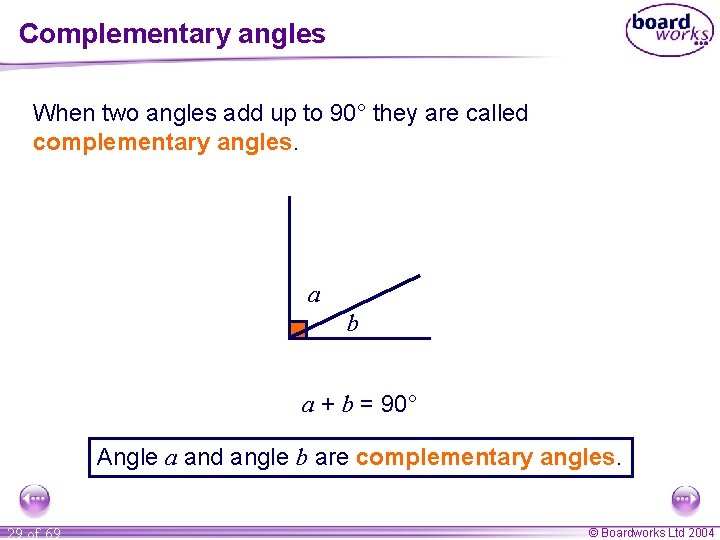
Complementary angles When two angles add up to 90° they are called complementary angles. a b a + b = 90° Angle a and angle b are complementary angles. 29 of 69 © Boardworks Ltd 2004

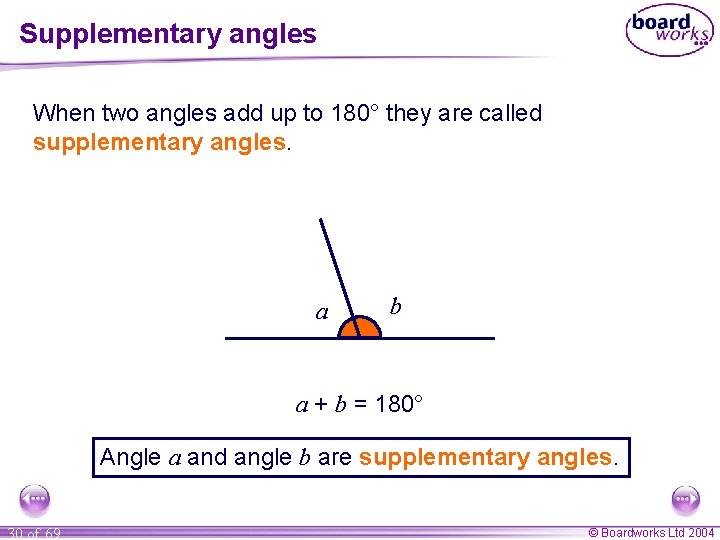
Supplementary angles When two angles add up to 180° they are called supplementary angles. a b a + b = 180° Angle a and angle b are supplementary angles. 30 of 69 © Boardworks Ltd 2004

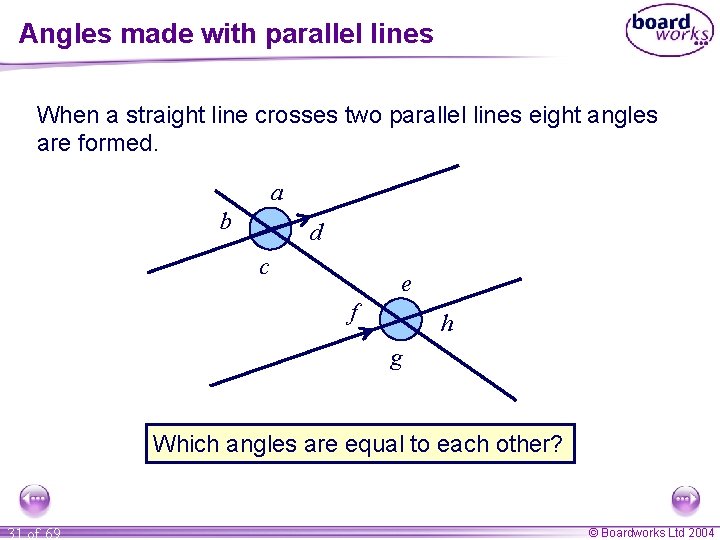
Angles made with parallel lines When a straight line crosses two parallel lines eight angles are formed. a b d c e f h g Which angles are equal to each other? 31 of 69 © Boardworks Ltd 2004

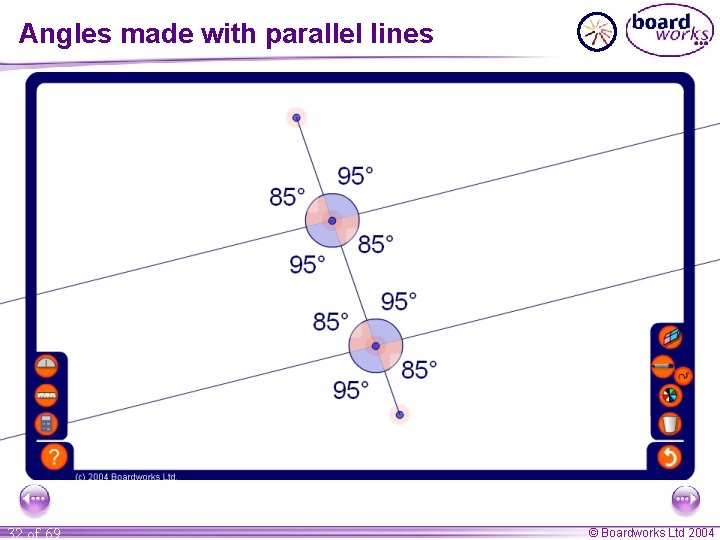
Angles made with parallel lines 32 of 69 © Boardworks Ltd 2004

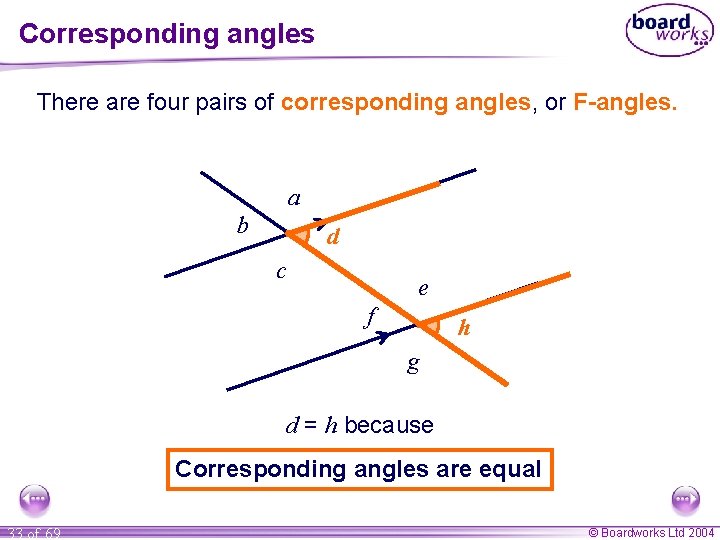
Corresponding angles There are four pairs of corresponding angles, or F-angles. a b d c e f h g d = h because Corresponding angles are equal 33 of 69 © Boardworks Ltd 2004

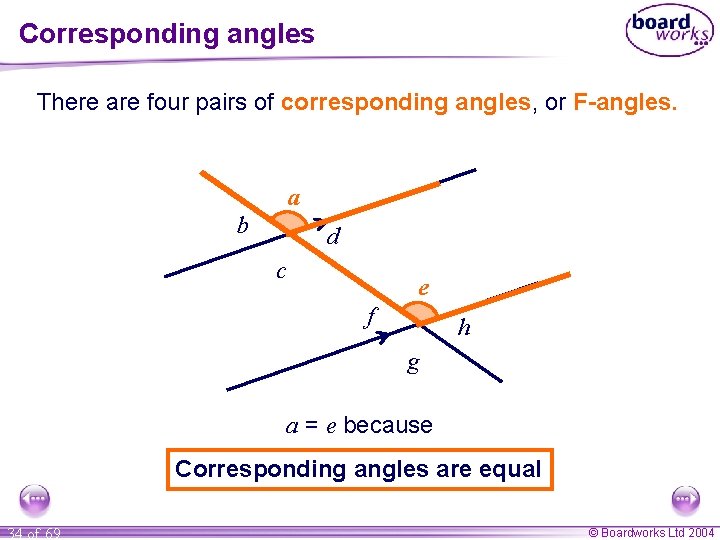
Corresponding angles There are four pairs of corresponding angles, or F-angles. a b d c e f h g a = e because Corresponding angles are equal 34 of 69 © Boardworks Ltd 2004

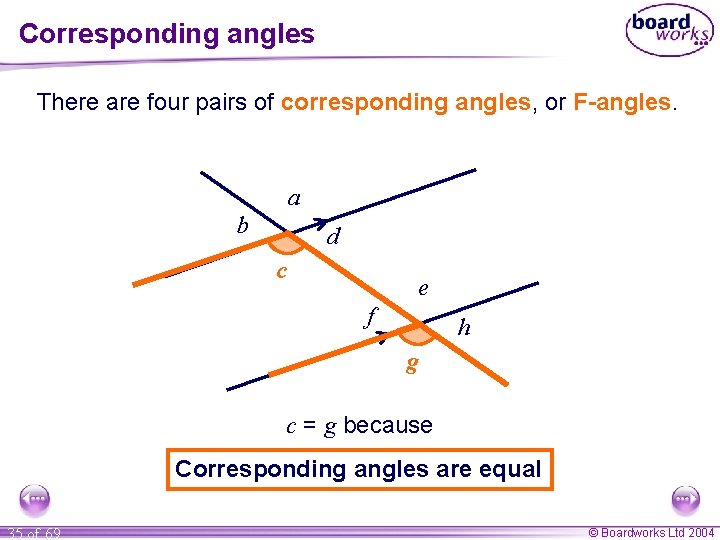
Corresponding angles There are four pairs of corresponding angles, or F-angles. a b d c e f h g c = g because Corresponding angles are equal 35 of 69 © Boardworks Ltd 2004

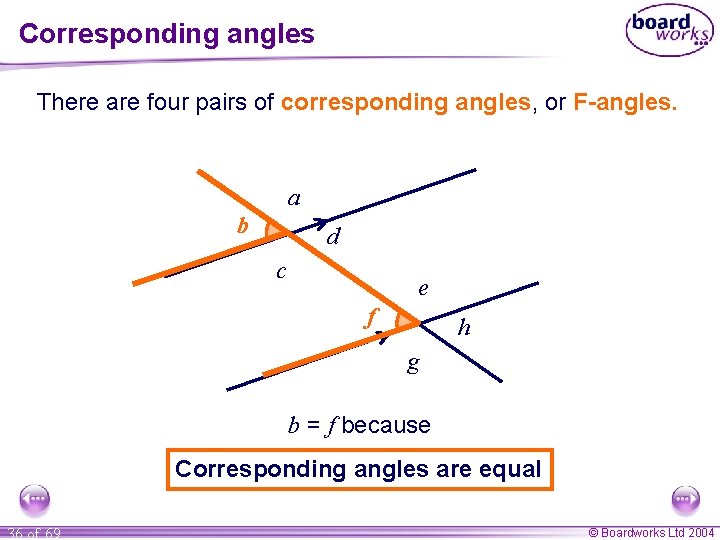
Corresponding angles There are four pairs of corresponding angles, or F-angles. a b d c e f h g b = f because Corresponding angles are equal 36 of 69 © Boardworks Ltd 2004

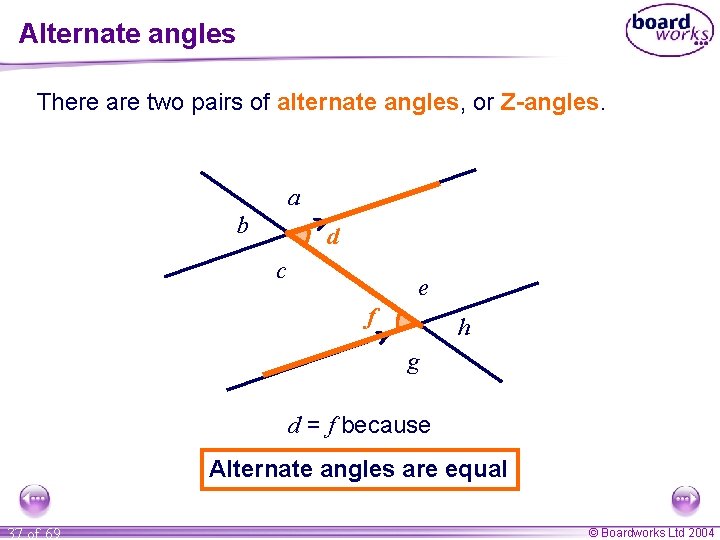
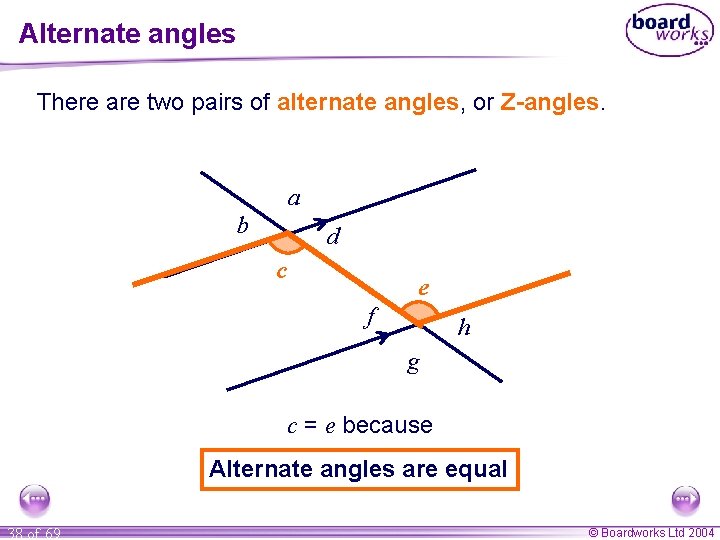
Alternate angles There are two pairs of alternate angles, or Z-angles. a b d c e f h g d = f because Alternate angles are equal 37 of 69 © Boardworks Ltd 2004

Alternate angles There are two pairs of alternate angles, or Z-angles. a b d c e f h g c = e because Alternate angles are equal 38 of 69 © Boardworks Ltd 2004

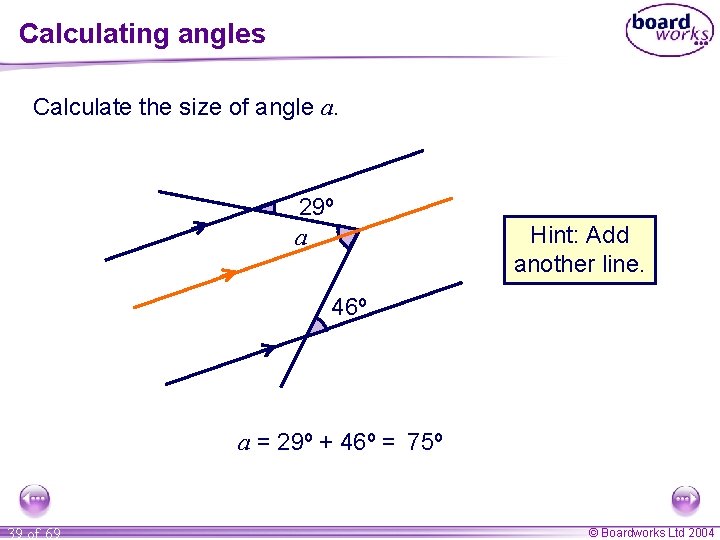
Calculating angles Calculate the size of angle a. 29º a Hint: Add another line. 46º a = 29º + 46º = 75º 39 of 69 © Boardworks Ltd 2004

Contents S 1 Lines and angles S 1. 1 Labelling lines and angles S 1. 2 Parallel and perpendicular lines S 1. 3 Calculating angles S 1. 4 Angles in polygons 40 of 69 © Boardworks Ltd 2004

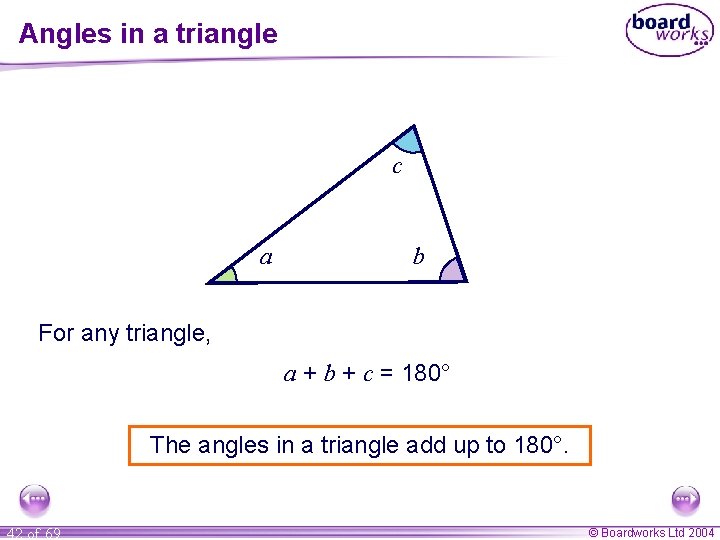
Angles in a triangle 41 of 69 © Boardworks Ltd 2004

Angles in a triangle c a b For any triangle, a + b + c = 180° The angles in a triangle add up to 180°. 42 of 69 © Boardworks Ltd 2004

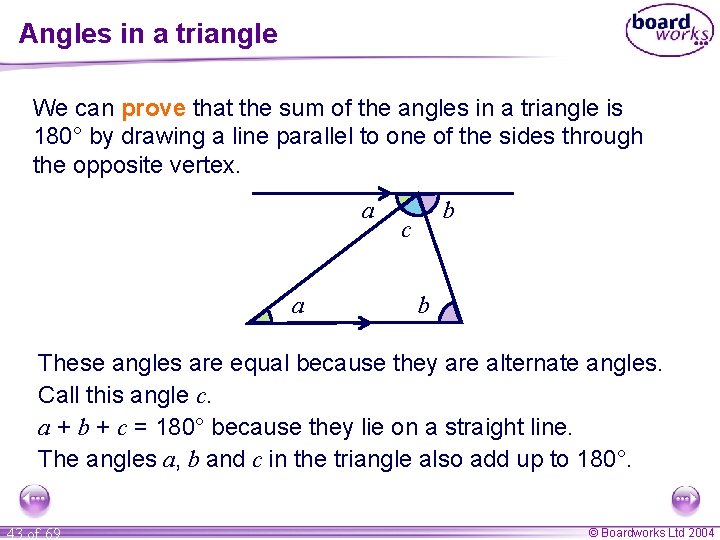
Angles in a triangle We can prove that the sum of the angles in a triangle is 180° by drawing a line parallel to one of the sides through the opposite vertex. a a b c b These angles are equal because they are alternate angles. Call this angle c. a + b + c = 180° because they lie on a straight line. The angles a, b and c in the triangle also add up to 180°. 43 of 69 © Boardworks Ltd 2004

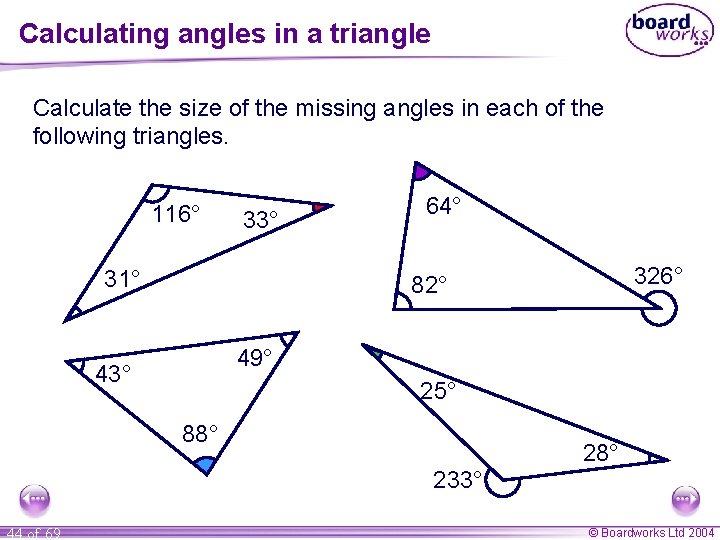
Calculating angles in a triangle Calculate the size of the missing angles in each of the following triangles. 116° a 33° 31° b 64° 49° 43° d 25° c 88° 233° 44 of 69 326° 82° 28° © Boardworks Ltd 2004

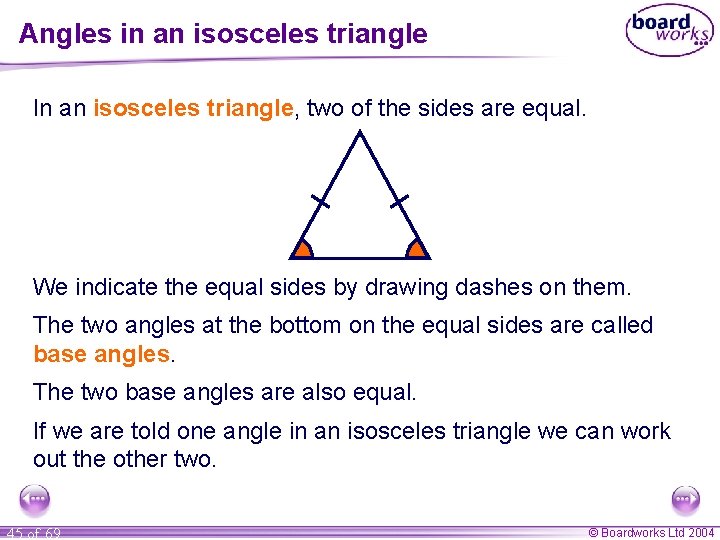
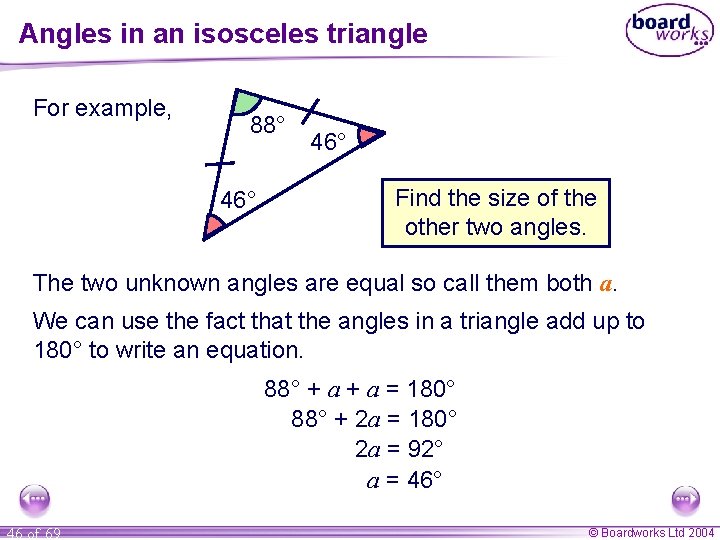
Angles in an isosceles triangle In an isosceles triangle, two of the sides are equal. We indicate the equal sides by drawing dashes on them. The two angles at the bottom on the equal sides are called base angles. The two base angles are also equal. If we are told one angle in an isosceles triangle we can work out the other two. 45 of 69 © Boardworks Ltd 2004

Angles in an isosceles triangle For example, 88° a 46° Find the size of the other two angles. The two unknown angles are equal so call them both a. We can use the fact that the angles in a triangle add up to 180° to write an equation. 88° + a = 180° 88° + 2 a = 180° 2 a = 92° a = 46° 46 of 69 © Boardworks Ltd 2004

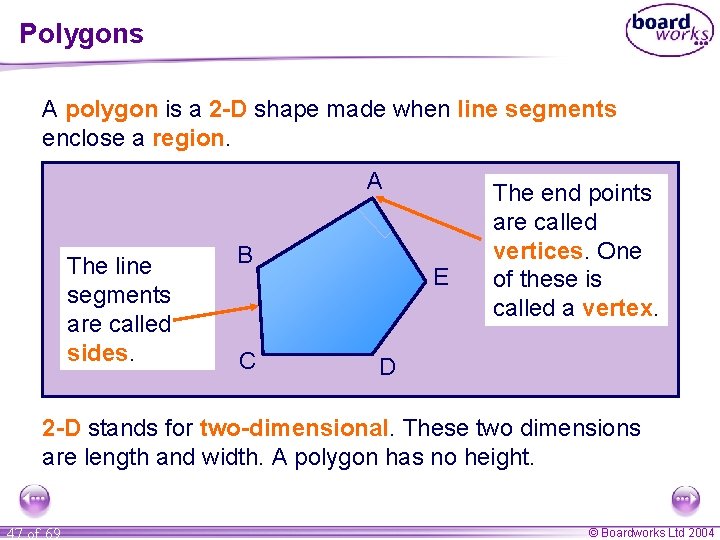
Polygons A polygon is a 2 -D shape made when line segments enclose a region. A The line segments are called sides. B C E The end points are called vertices. One of these is called a vertex. D 2 -D stands for two-dimensional. These two dimensions are length and width. A polygon has no height. 47 of 69 © Boardworks Ltd 2004

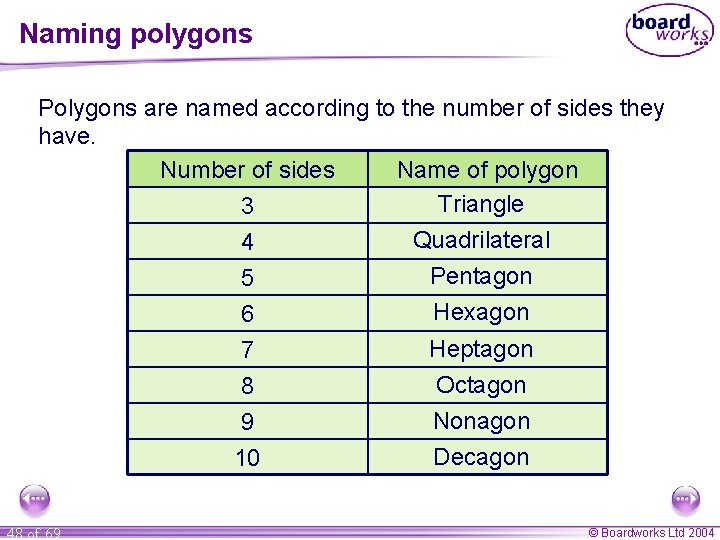
Naming polygons Polygons are named according to the number of sides they have. Number of sides Name of polygon Triangle 3 Quadrilateral 4 48 of 69 5 Pentagon 6 7 8 9 10 Hexagon Heptagon Octagon Nonagon Decagon © Boardworks Ltd 2004

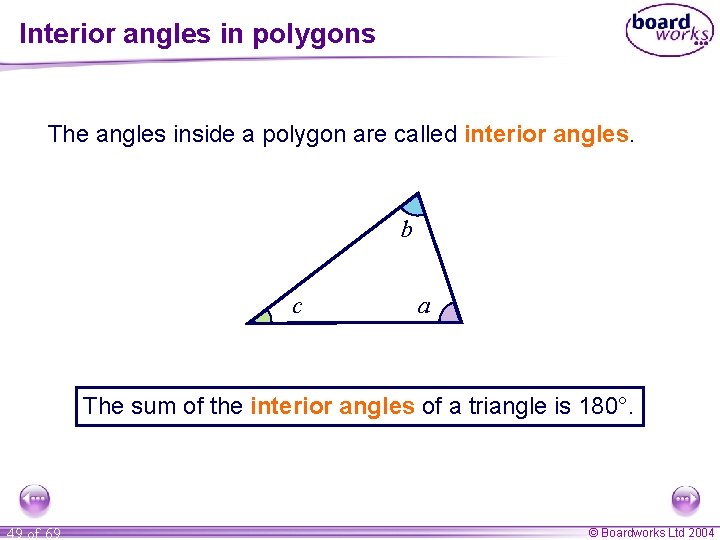
Interior angles in polygons The angles inside a polygon are called interior angles. b c a The sum of the interior angles of a triangle is 180°. 49 of 69 © Boardworks Ltd 2004

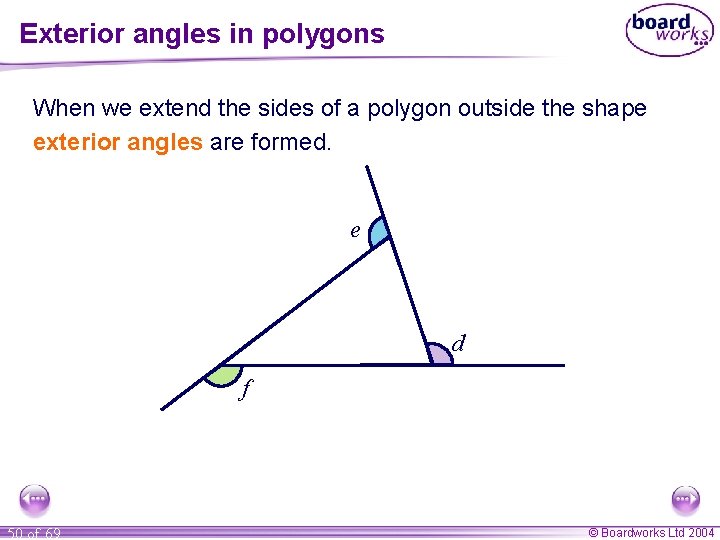
Exterior angles in polygons When we extend the sides of a polygon outside the shape exterior angles are formed. e d f 50 of 69 © Boardworks Ltd 2004

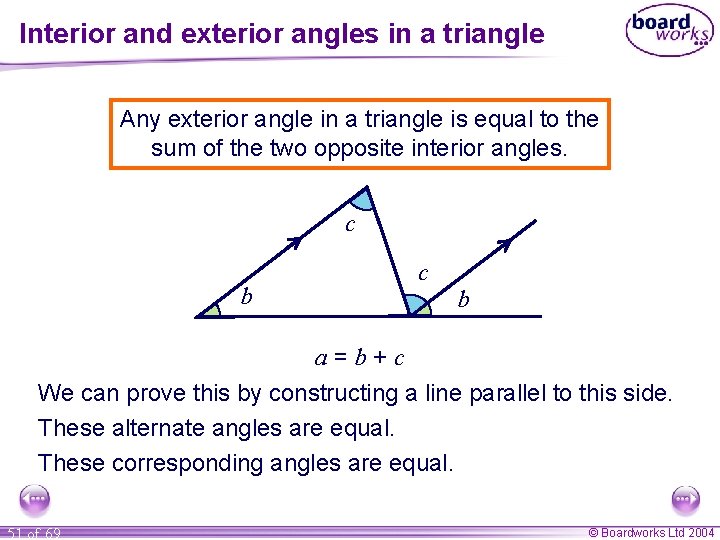
Interior and exterior angles in a triangle Any exterior angle in a triangle is equal to the sum of the two opposite interior angles. c ca b b a=b+c We can prove this by constructing a line parallel to this side. These alternate angles are equal. These corresponding angles are equal. 51 of 69 © Boardworks Ltd 2004

Interior and exterior angles in a triangle 52 of 69 © Boardworks Ltd 2004

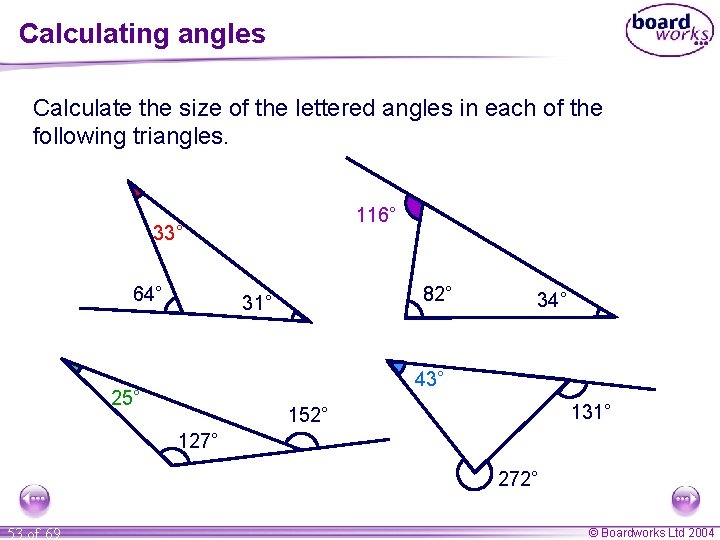
Calculating angles Calculate the size of the lettered angles in each of the following triangles. b 116° a 33° 64° 82° 31° 34° c 43° d 25° 131° 152° 127° 272° 53 of 69 © Boardworks Ltd 2004

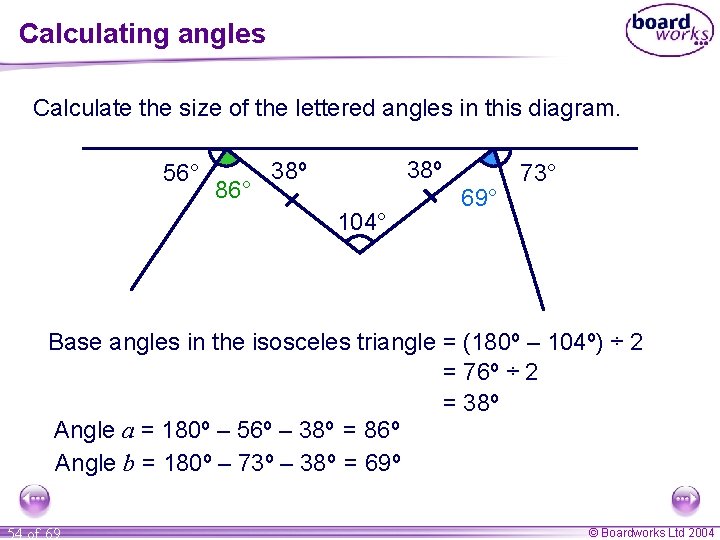
Calculating angles Calculate the size of the lettered angles in this diagram. 56° a 86° 38º 104° b 69° 73° Base angles in the isosceles triangle = (180º – 104º) ÷ 2 = 76º ÷ 2 = 38º Angle a = 180º – 56º – 38º = 86º Angle b = 180º – 73º – 38º = 69º 54 of 69 © Boardworks Ltd 2004

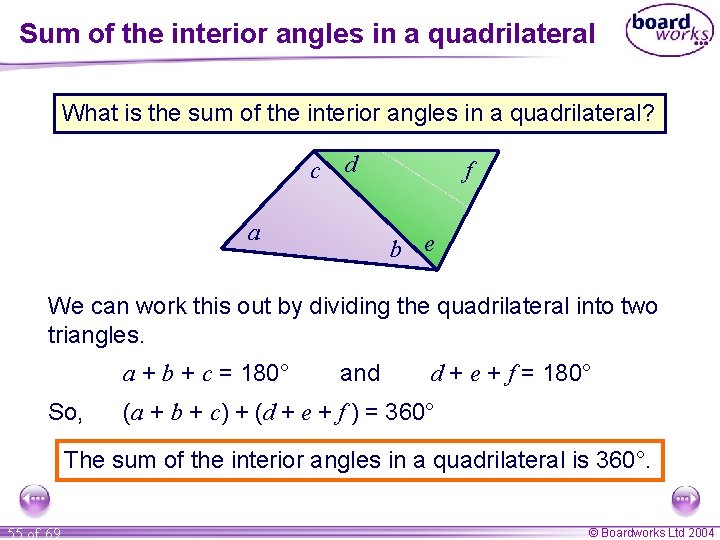
Sum of the interior angles in a quadrilateral What is the sum of the interior angles in a quadrilateral? c d a f b e We can work this out by dividing the quadrilateral into two triangles. a + b + c = 180° So, and d + e + f = 180° (a + b + c) + (d + e + f ) = 360° The sum of the interior angles in a quadrilateral is 360°. 55 of 69 © Boardworks Ltd 2004

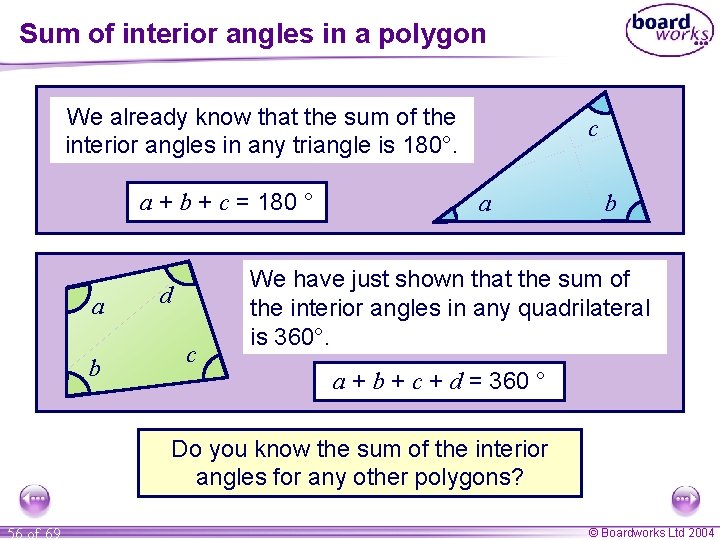
Sum of interior angles in a polygon We already know that the sum of the interior angles in any triangle is 180°. a + b + c = 180 ° a b d c c a b We have just shown that the sum of the interior angles in any quadrilateral is 360°. a + b + c + d = 360 ° Do you know the sum of the interior angles for any other polygons? 56 of 69 © Boardworks Ltd 2004

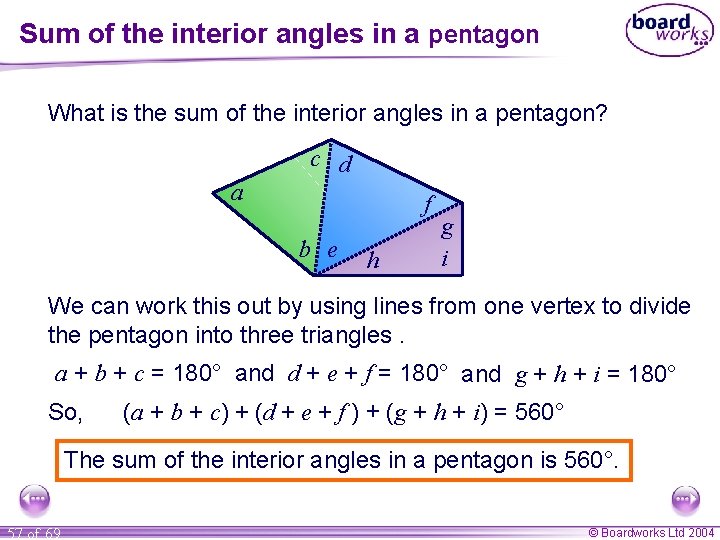
Sum of the interior angles in a pentagon What is the sum of the interior angles in a pentagon? c d a f b e h g i We can work this out by using lines from one vertex to divide the pentagon into three triangles. a + b + c = 180° and d + e + f = 180° and g + h + i = 180° So, (a + b + c) + (d + e + f ) + (g + h + i) = 560° The sum of the interior angles in a pentagon is 560°. 57 of 69 © Boardworks Ltd 2004

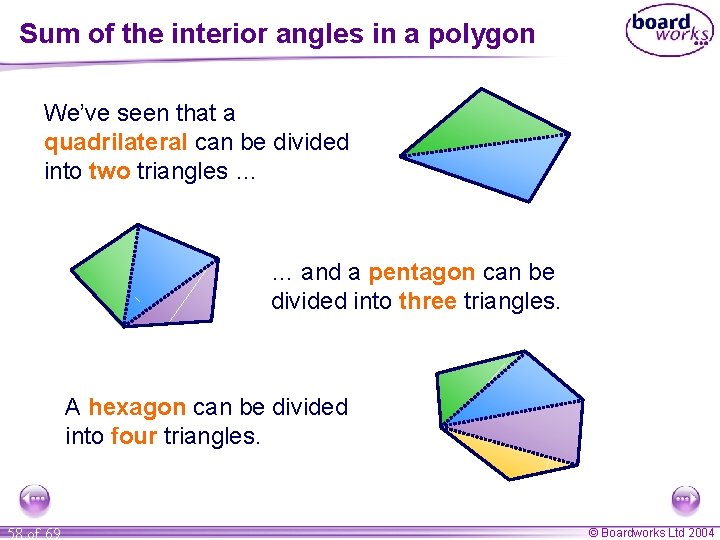
Sum of the interior angles in a polygon We’ve seen that a quadrilateral can be divided into two triangles … … and a pentagon can be divided into three triangles. many triangles can a AHow hexagon can be divided hexagon be divided into? into four triangles. 58 of 69 © Boardworks Ltd 2004

Sum of the interior angles in a polygon The number of triangles that a polygon can be divided into is always two less than the number of sides. We can say that: A polygon with n sides can be divided into (n – 2) triangles. The sum of the interior angles in a triangle is 180°. So, The sum of the interior angles in an n-sided polygon is (n – 2) × 180°. 59 of 69 © Boardworks Ltd 2004

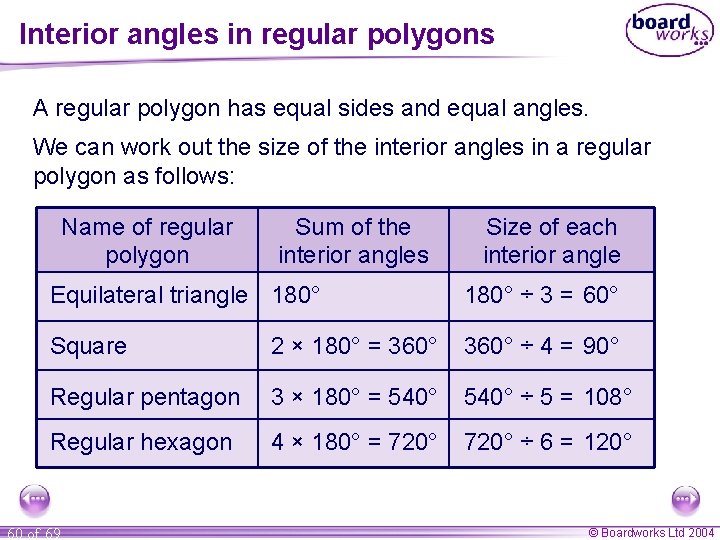
Interior angles in regular polygons A regular polygon has equal sides and equal angles. We can work out the size of the interior angles in a regular polygon as follows: Name of regular polygon Sum of the interior angles Size of each interior angle Equilateral triangle 180° ÷ 3 = 60° Square 2 × 180° = 360° ÷ 4 = 90° Regular pentagon 3 × 180° = 540° ÷ 5 = 108° Regular hexagon 4 × 180° = 720° ÷ 6 = 120° 60 of 69 © Boardworks Ltd 2004

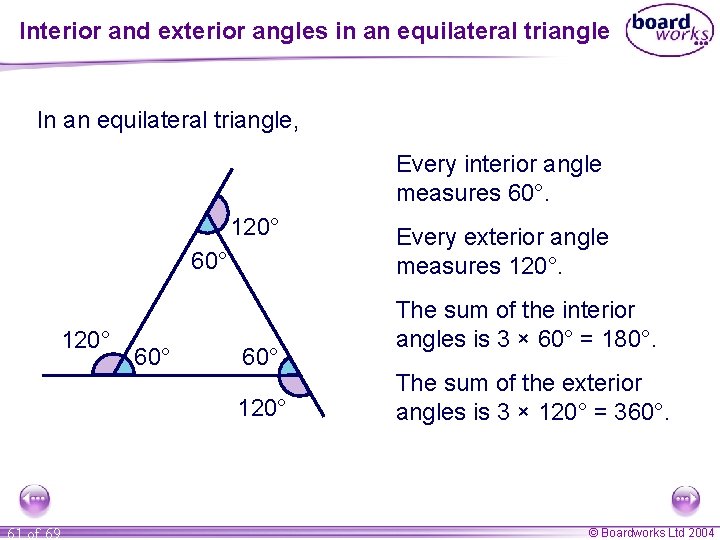
Interior and exterior angles in an equilateral triangle In an equilateral triangle, Every interior angle measures 60°. 120° 60° 60° 120° 61 of 69 Every exterior angle measures 120°. The sum of the interior angles is 3 × 60° = 180°. The sum of the exterior angles is 3 × 120° = 360°. © Boardworks Ltd 2004

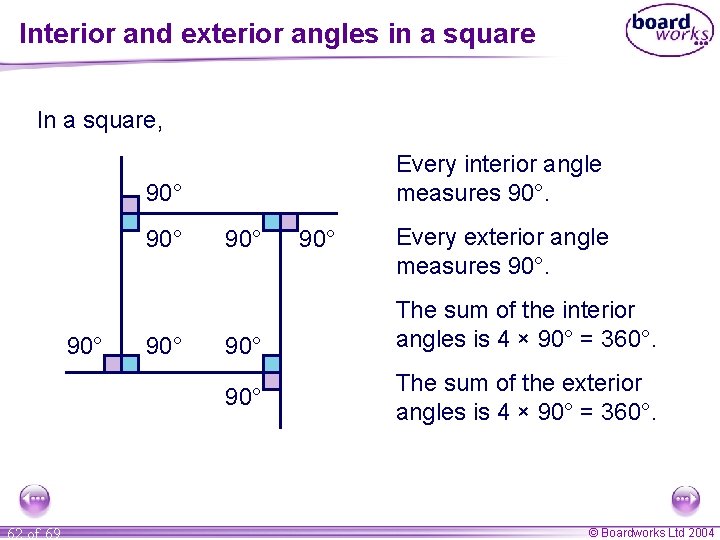
Interior and exterior angles in a square In a square, Every interior angle measures 90° 90° 62 of 69 90° Every exterior angle measures 90°. The sum of the interior angles is 4 × 90° = 360°. The sum of the exterior angles is 4 × 90° = 360°. © Boardworks Ltd 2004

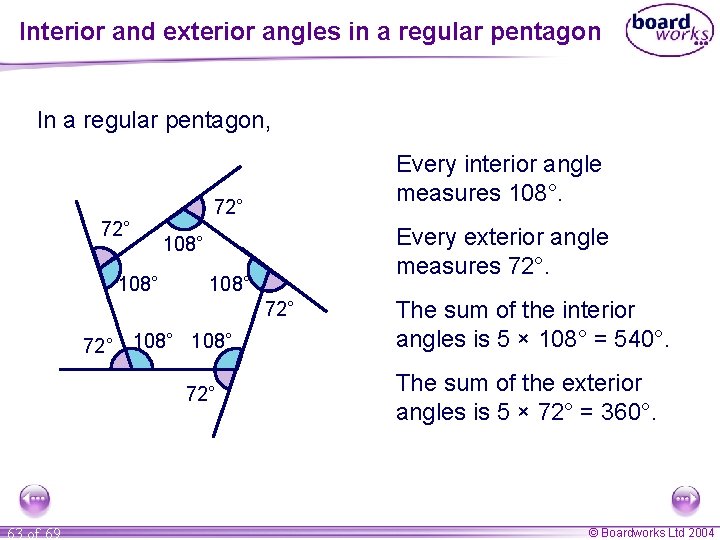
Interior and exterior angles in a regular pentagon In a regular pentagon, Every interior angle measures 108°. 72° 108° Every exterior angle measures 72°. 108° 72° 63 of 69 The sum of the interior angles is 5 × 108° = 540°. The sum of the exterior angles is 5 × 72° = 360°. © Boardworks Ltd 2004

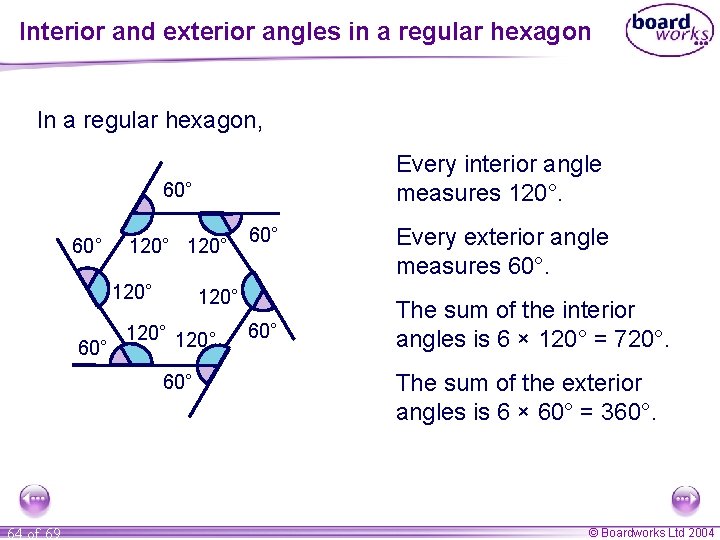
Interior and exterior angles in a regular hexagon In a regular hexagon, Every interior angle measures 120°. 60° 120° 120° 60° 64 of 69 60° Every exterior angle measures 60°. The sum of the interior angles is 6 × 120° = 720°. The sum of the exterior angles is 6 × 60° = 360°. © Boardworks Ltd 2004

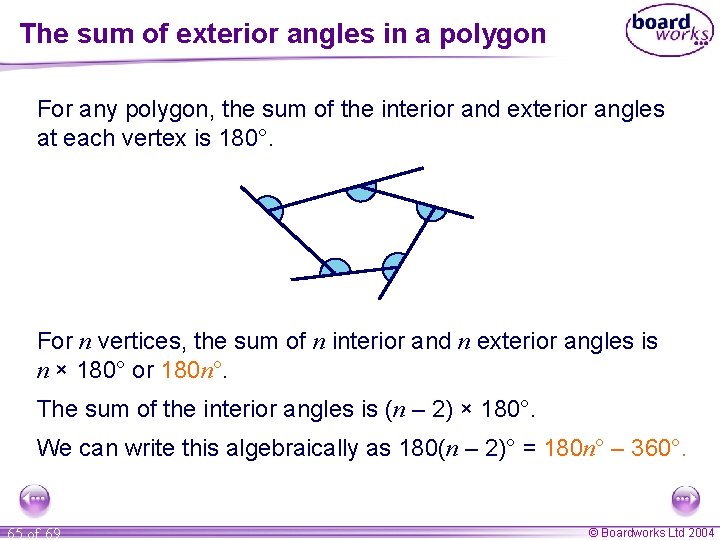
The sum of exterior angles in a polygon For any polygon, the sum of the interior and exterior angles at each vertex is 180°. For n vertices, the sum of n interior and n exterior angles is n × 180° or 180 n°. The sum of the interior angles is (n – 2) × 180°. We can write this algebraically as 180(n – 2)° = 180 n° – 360°. 65 of 69 © Boardworks Ltd 2004

The sum of exterior angles in a polygon If the sum of both the interior and the exterior angles is 180 n° and the sum of the interior angles is 180 n° – 360°, the sum of the exterior angles is the difference between these two. The sum of the exterior angles = 180 n° – (180 n° – 360°) = 180 n° – 180 n° + 360° = 360° The sum of the exterior angles in a polygon is 360°. 66 of 69 © Boardworks Ltd 2004

Take Turtle for a walk 67 of 69 © Boardworks Ltd 2004

Find the number of sides 68 of 69 © Boardworks Ltd 2004

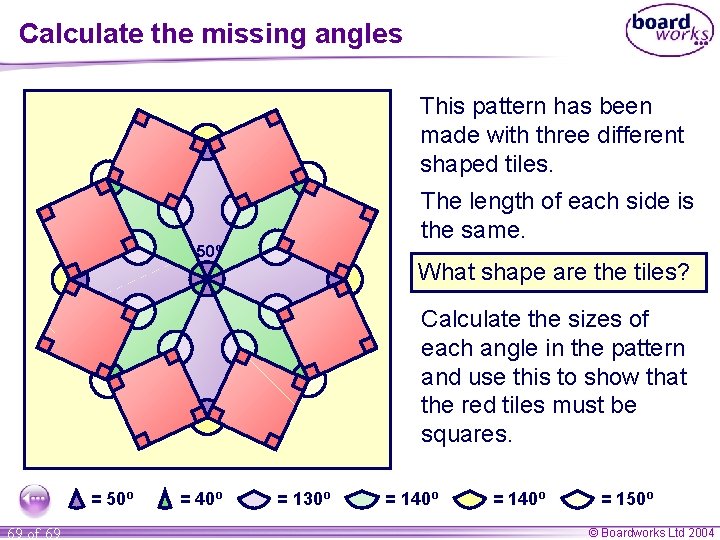
Calculate the missing angles This pattern has been made with three different shaped tiles. The length of each side is the same. 50º What shape are the tiles? Calculate the sizes of each angle in the pattern and use this to show that the red tiles must be squares. = 50º 69 of 69 = 40º = 130º = 140º = 150º © Boardworks Ltd 2004