KS 091201 MATEMATIKA DISKRIT DISCRETE MATHEMATICS GRAPH THEORY

KS 091201 MATEMATIKA DISKRIT (DISCRETE MATHEMATICS ) GRAPH THEORY Discrete Math Team

2 -- KS 091201 Outline Simple Graph Directed Graph Djikstra Algorithm

What are Graphs? General meaning in everyday math: A plot or chart of numerical data using a coordinate system. Technical meaning in discrete mathematics: A particular class of discrete structures (to be defined) that is useful for representing relations and has a convenient graphical representation.

Applications of Graphs Potentially anything (graphs can represent relations; relations can describe the extension of any predicate). Apps in networking, scheduling, flow optimization, circuit design, path planning. Genealogy analysis, computer game-playing, program compilation, object-oriented design, …

Simple Graphs Correspond A to symmetric binary relations R. simple graph G=(V, E) consists of: a set V of vertices or nodes (V corresponds to the universe of the relation R), a set E of edges / arcs / links: unordered pairs of elements u, v V, such that u. Rv.

Example of a Simple Graph Let V be the set of states in the far-southeastern U. S. : V={FL, Let GA, AL, MS, LA, SC, TN, NC} E={{u, v}|u adjoins v} ={{FL, GA}, {FL, AL}, {FL, MS}, {FL, LA}, {GA, AL}, {AL, MS}, { MS, LA}, {GA, SC}, {GA, TN}, {SC, NC}, {NC, TN}, {MS, AL}} TN MS AL NC SC GA LA FL

Directed Graphs Correspond to arbitrary binary relations R, which need not be symmetric. A directed graph (V, E) consists of a set of vertices V and a binary relation E on V. E. g. : V = people, E={(x, y) | x loves y}

Graph Terminology Adjacent connects endpoints degree initial terminal in-degree, out-degree subgraph, union.

Adjacency Let G be an undirected graph with edge set E. Let e E be (or map to) the pair {u, v}. Then we say: u, v are adjacent / neighbors / connected. Edge e is incident with vertices u and v. Edge e connects u and v. Vertices u and v are endpoints of edge e.

Degree of a Vertex Let G be an undirected graph, v V a vertex. The degree of v, deg(v), is its number of incident edges. (Except that any self-loops are counted twice. ) A vertex with degree 0 is isolated. A vertex of degree 1 is pendant.

Handshaking Theorem Let G be an undirected graph with vertex set V and edge set E. Then Corollary: Any undirected graph has an even number of vertices of odd degree.

Directed Adjacency Let G be a directed graph, and let e be an edge of G that is (or maps to) (u, v). Then we say: u is adjacent to v, v is adjacent from u e comes from u, e goes to v. e connects u to v, e goes from u to v the initial vertex of e is u the terminal vertex of e is v

Directed Degree Let G be a directed graph, v a vertex of G. in-degree of v, deg (v), is the number of edges going to v. The out-degree of v, deg (v), is the number of edges coming from v. The degree of v, deg(v) deg (v)+deg (v), is the sum of v’s in-degree and out-degree. The

Directed Handshaking Theorem Let G be a directed graph with vertex set V and edge set E. Then: Note that the degree of a node is unchanged by whether we consider its edges to be directed or undirected.

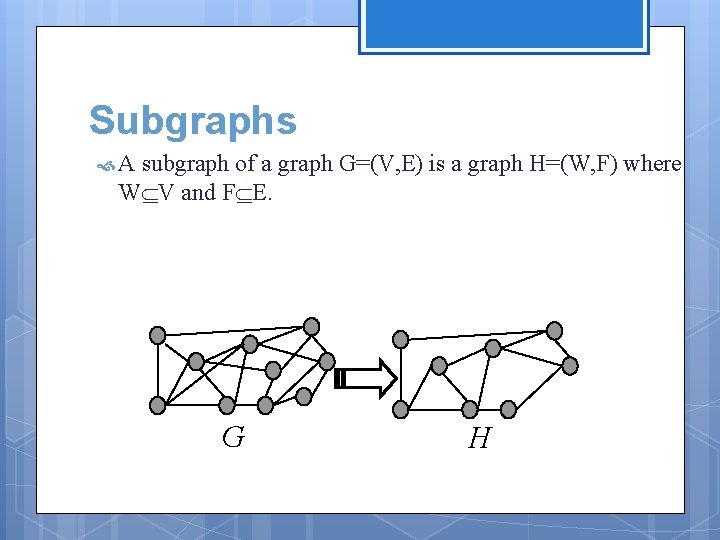
Subgraphs A subgraph of a graph G=(V, E) is a graph H=(W, F) where W V and F E. G H

Graph Unions union G 1 G 2 of two simple graphs G 1=(V 1, E 1) and G 2=(V 2, E 2) is the simple graph (V 1 V 2, E 1 E 2). The

Graph Representations Adjacency lists. Adjacency matrices. Incidence matrices.

Adjacency Lists A table with 1 row per vertex, listing its adjacent vertices. b a c d e f

Directed Adjacency Lists 1 row per node, listing the terminal nodes of each edge incident from that node.

Adjacency Matrices Matrix A=[aij], where aij is 1 if {vi, vj} is an edge of G, 0 otherwise.

Connectivity In an undirected graph, a path of length n from u to v is a sequence of adjacent edges going from vertex u to vertex v. A path is a circuit if u=v. A path traverses the vertices along it. A path is simple if it contains no edge more than once.

Paths in Directed Graphs Same as in undirected graphs, but the path must go in the direction of the arrows.

Connectedness An undirected graph is connected iff there is a path between every pair of distinct vertices in the graph. Theorem: There is a simple path between any pair of vertices in a connected undirected graph.

Review: Graph Theory Types of graphs Graph terminology Graph representation Connectivity

Graphs - Shortest Paths Application In a graph in which edges have costs. . Find the shortest path from a source to a destination Surprisingly. . While finding the shortest path from a source to one destination, we can find the shortest paths to all over destinations as well! Common algorithm for single-source shortest paths is due to Edsger Dijkstra

Dijkstra’s Algorithm - Data Structures For a graph, G = ( V, E ) Dijkstra’s algorithm keeps two sets of vertices: S V-S Vertices whose shortest paths have already been determined Remainder Also d p Best estimates of shortest path to each vertex Predecessors for each vertex

Predecessor Sub-graph Array of vertex indices, p[j], j = 1. . |V| p[j] contains the pre-decessor for node j j’s predecessor is in p[p[j]], and so on. . The edges in the pre-decessor sub-graph are ( p[j], j )

Dijkstra’s Algorithm - Operation Initial estimates are all ¥ Initialise d and p For each vertex, j, in V dj = ¥ · pj = nil Source distance, ds = 0 No connections Set S to empty While V-S is not empty Sort V-S based on d Add u, the closest vertex in V-S, to S Relax all the vertices still in V-S connected to u Add s first!

Dijkstra’s Algorithm - Operation Initialise d and p For each vertex, j, in V dj = ¥ · pj = nil Initial estimates are all ¥ No connections Source distance, ds = 0 Set S to empty While V-S is not empty Sort V-S based on d Add u, the closest vertex in V-S, to S Relax all the vertices still in V-S connected to u Add s first!

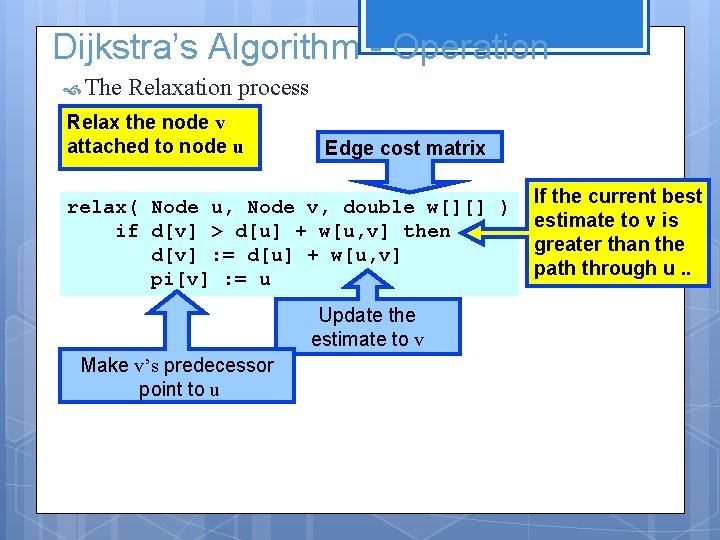
Dijkstra’s Algorithm - Operation The Relaxation process Relax the node v attached to node u Edge cost matrix relax( Node u, Node v, double w[][] ) if d[v] > d[u] + w[u, v] then d[v] : = d[u] + w[u, v] pi[v] : = u Update the estimate to v Make v’s predecessor point to u If the current best estimate to v is greater than the path through u. .

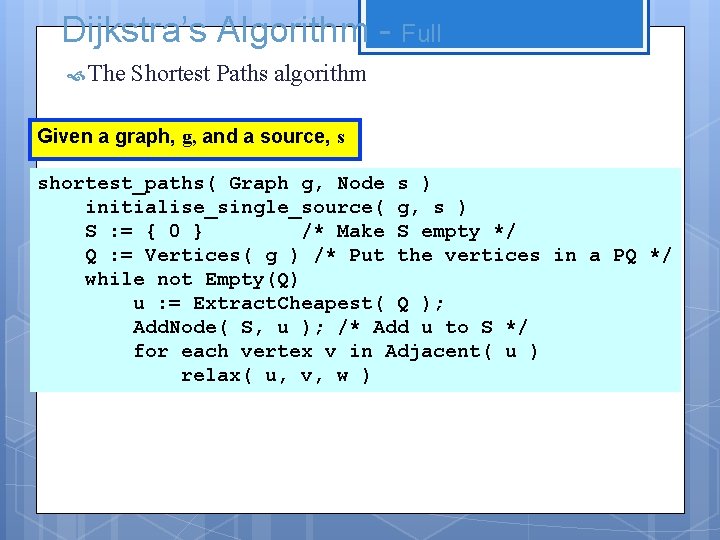
Dijkstra’s Algorithm - Full The Shortest Paths algorithm Given a graph, g, and a source, s shortest_paths( Graph g, Node s ) initialise_single_source( g, s ) S : = { 0 } /* Make S empty */ Q : = Vertices( g ) /* Put the vertices in a PQ */ while not Empty(Q) u : = Extract. Cheapest( Q ); Add. Node( S, u ); /* Add u to S */ for each vertex v in Adjacent( u ) relax( u, v, w )

Dijkstra’s Algorithm - Initialise The Shortest Paths algorithm Given a graph, g, and a source, s Initialise d, p, S, vertex Q shortest_paths( Graph g, Node s ) initialise_single_source( g, s ) S : = { 0 } /* Make S empty */ Q : = Vertices( g ) /* Put the vertices in a PQ */ while not Empty(Q) u : = Extract. Cheapest( Q ); Add. Node( S, u ); /* Add u to S */ for each vertex v in Adjacent( u ) relax( u, v, w )

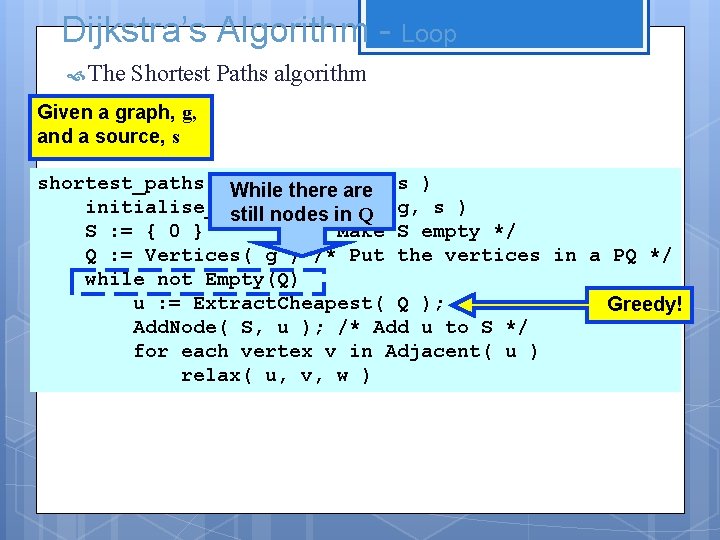
Dijkstra’s Algorithm - Loop The Shortest Paths algorithm Given a graph, g, and a source, s shortest_paths( Graph g, Node While there are s ) initialise_single_source( still nodes in Q g, s ) S : = { 0 } /* Make S empty */ Q : = Vertices( g ) /* Put the vertices in a PQ */ while not Empty(Q) u : = Extract. Cheapest( Q ); Greedy! Add. Node( S, u ); /* Add u to S */ for each vertex v in Adjacent( u ) relax( u, v, w )

Dijkstra’s Algorithm - Relax neighbours The Shortest Paths algorithm Given a graph, g, and a source, s Update the estimate of the shortest_paths( Graph g, paths Node tos ) shortest initialise_single_source( all nodes g, s ) S : = { 0 } /* Make attached to u S empty */ Q : = Vertices( g ) /* Put the vertices in a PQ */ while not Empty(Q) u : = Extract. Cheapest( Q ); Greedy! Add. Node( S, u ); /* Add u to S */ for each vertex v in Adjacent( u ) relax( u, v, w )

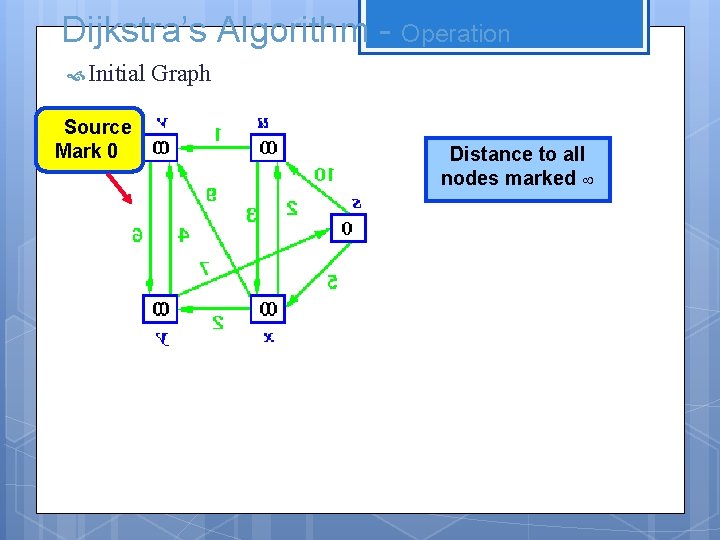
Dijkstra’s Algorithm - Operation Initial Source Mark 0 Graph Distance to all nodes marked ¥

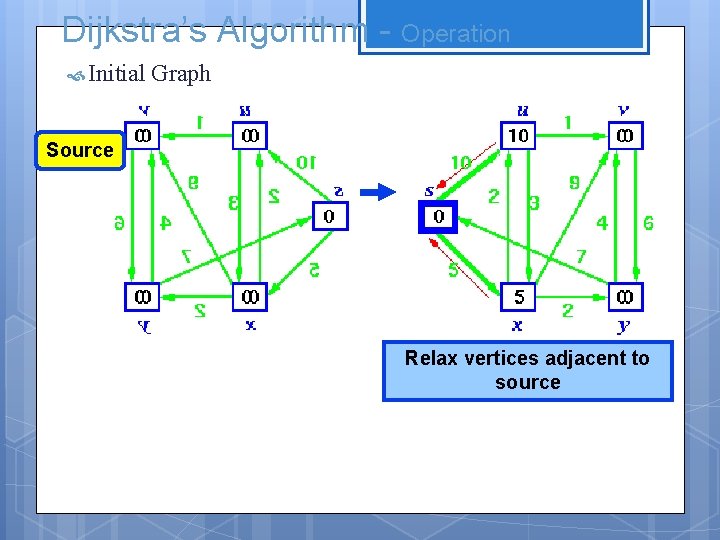
Dijkstra’s Algorithm - Operation Initial Graph Source Relax vertices adjacent to source

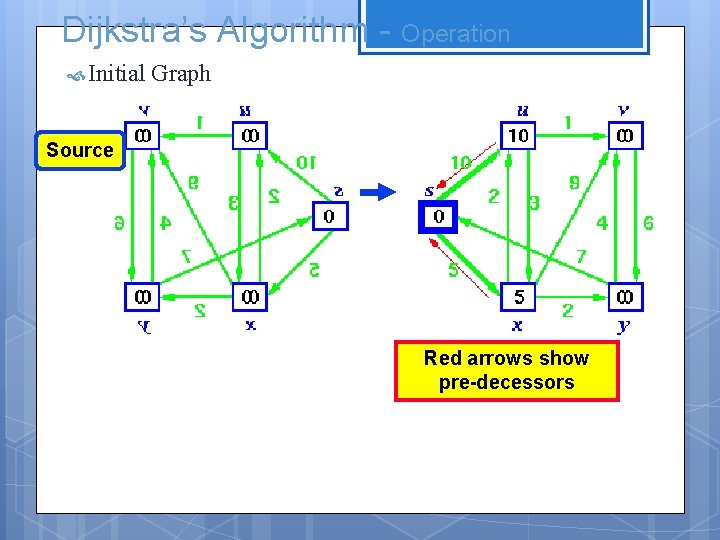
Dijkstra’s Algorithm - Operation Initial Graph Source Red arrows show pre-decessors

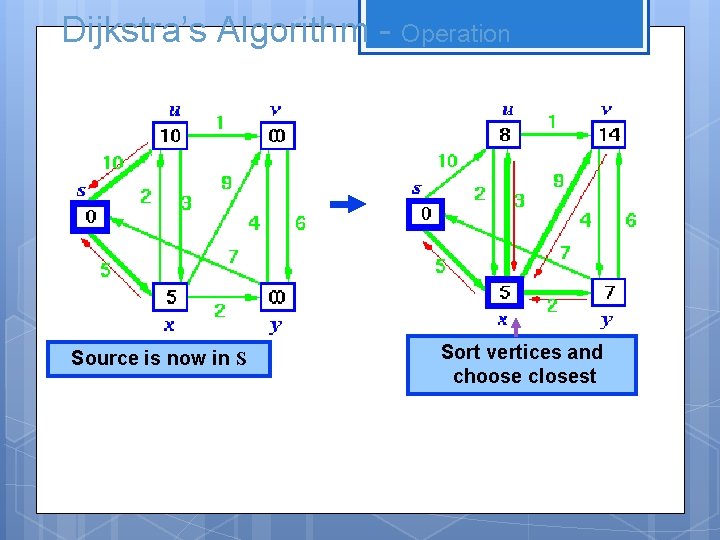
Dijkstra’s Algorithm - Operation Source is now in S Sort vertices and choose closest

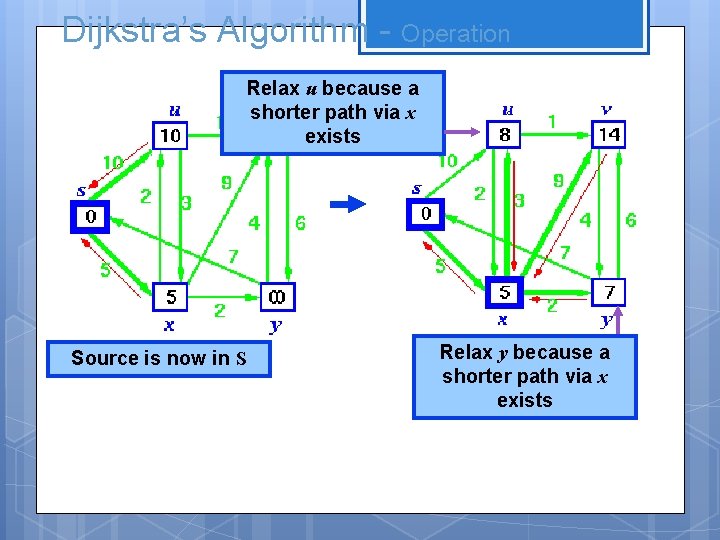
Dijkstra’s Algorithm - Operation Relax u because a shorter path via x exists Source is now in S Relax y because a shorter path via x exists

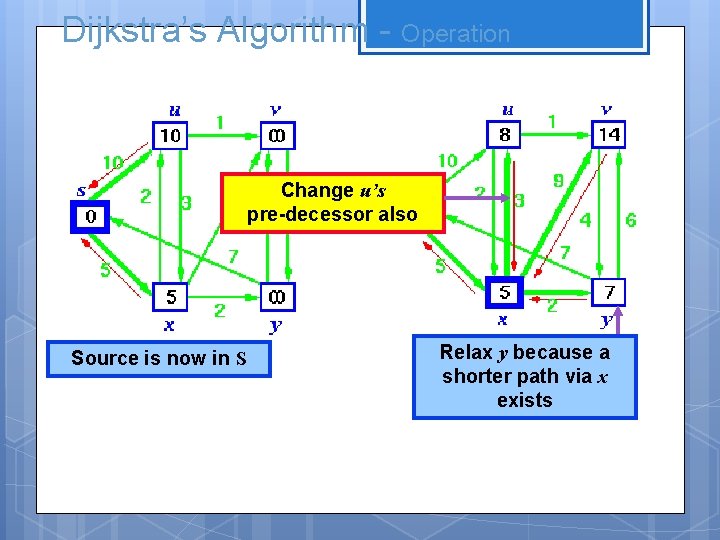
Dijkstra’s Algorithm - Operation Change u’s pre-decessor also Source is now in S Relax y because a shorter path via x exists

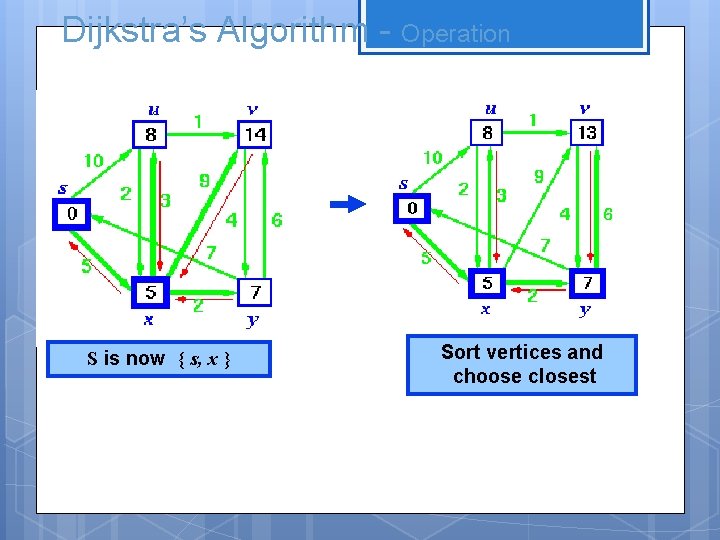
Dijkstra’s Algorithm - Operation S is now { s, x } Sort vertices and choose closest

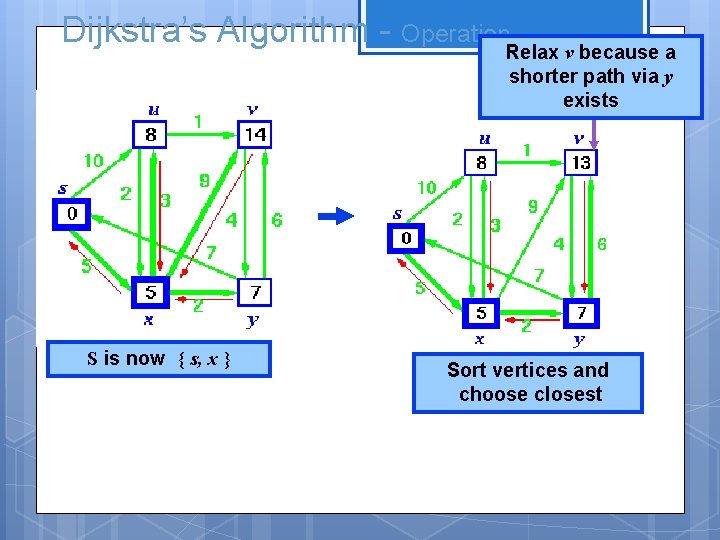
Dijkstra’s Algorithm - Operation. Relax v because a shorter path via y exists S is now { s, x } Sort vertices and choose closest

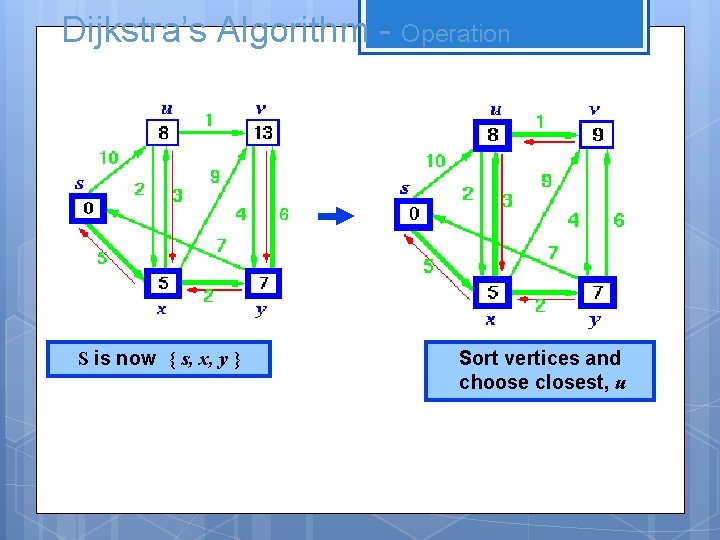
Dijkstra’s Algorithm - Operation S is now { s, x, y } Sort vertices and choose closest, u

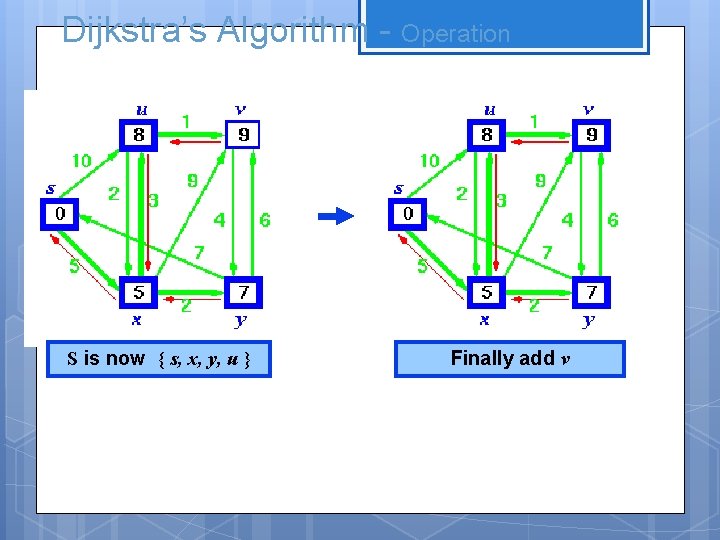
Dijkstra’s Algorithm - Operation S is now { s, x, y, u } Finally add v

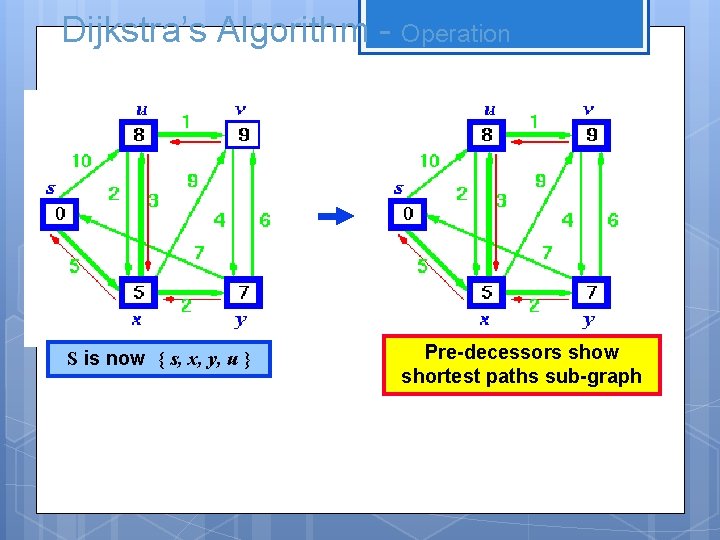
Dijkstra’s Algorithm - Operation S is now { s, x, y, u } Pre-decessors show shortest paths sub-graph

Dijkstra’s Algorithm - Proof Greedy Proof Lemma Algorithm by contradiction best 1 Shortest paths are composed of shortest paths Proof If there was a shorter path than any sub-path, then substitution of that path would make the whole path shorter

Dijkstra’s Algorithm - Proof Denote d(s, v) - the cost of the shortest path from s to v Lemma 2 If s®. . . ®u®v is a shortest path from s to v, then after u has been added to S and relax(u, v, w) called, d[v] = d(s, v) and d[v] is not changed thereafter. Proof Follows from the fact that at all times d[v] ³ d(s, v) See Cormen (or any other text) for the details

Dijkstra’s Algorithm - Proof Using Lemma 2 After running Dijkstra’s algorithm, we assert d[v] = d(s, v) for all v Proof (by contradiction) Suppose that u is the first vertex added to S for which d[u] ¹ d(s, u) Note v is not s because d[s] = 0 There must be a path s®. . . ®u, otherwise d[u] would be ¥ Since there’s a path, there must be a shortest path

Dijkstra’s Algorithm - Proof (by contradiction) Suppose that u is the first vertex added to S for which d[u] ¹ d(s, u) Let s®x®y®u be the shortest path s®u, where x is in S and y is the first outside S When x was added to S, d[x] = d(s, x) Edge x®y was relaxed at that time, so d[y] = d(s, y)

Dijkstra’s Algorithm - Proof (by contradiction) Edge x®y was relaxed at that time, so d[y] = d(s, y) £ d(s, u) £ d[u] But, when we chose u, both u and y where in V-S, so d[u] £ d[y] (otherwise we would have chosen y) Thus the inequalities must be equalities d[y] = d(s, y) = d(s, u) = d[u] And our hypothesis (d[u] ¹ d(s, u)) is contradicted!

Dijkstra’s Algorithm - Time Complexity Dijkstra’s Algorithm Similar to MST algorithms Key step is sort on the edges Complexity is O( (|E|+|V|)log|V| ) or O( n 2 log n ) for a dense graph with n = |V|