Kruskals and Dijkstras Algorithm Kruskals Algorithm v Kruskals

Kruskal’s and Dijkstra’s Algorithm

Kruskal’s Algorithm v. Kruskal's algorithm is an algorithm in graph theory that finds a minimum spanning tree for a connected weighted graph. v. If the graph is not connected, then it finds a minimum spanning forest (a minimum spanning tree for each connected component). v. Kruskal's algorithm is an example of a greedy algorithm. v. You can look at all of the edges at once v. You can hold all of the vertices at once 1

Kruskal’s Algorithm ALGORITHM Kruskal(G) //Kruskal’s Algorithm for constructing a minimum spanning tree //Input: A weighted connected graph G=(V, E) //Output: ET – the set of edges composing a minimum spanning tree of G. Sort E in the non-decreasing order of the edges weights w(ei 1 )≤ …≤ w(e i|E|) ET ← 0; encounter ← 0; k ← 0 While encounter < |v|-1 do k ← k+1 if ET U {eik} is acyclic then ET ← ET U eik; encounter ← encounter +1 return ET 2

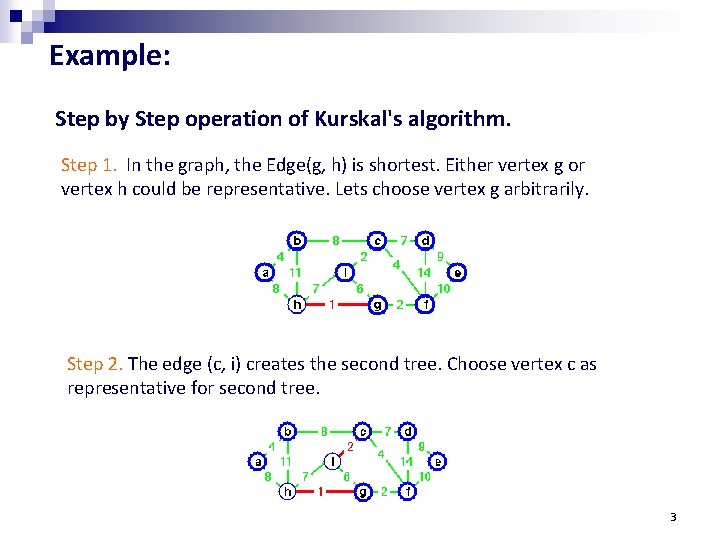
Example: Step by Step operation of Kurskal's algorithm. Step 1. In the graph, the Edge(g, h) is shortest. Either vertex g or vertex h could be representative. Lets choose vertex g arbitrarily. Step 2. The edge (c, i) creates the second tree. Choose vertex c as representative for second tree. 3

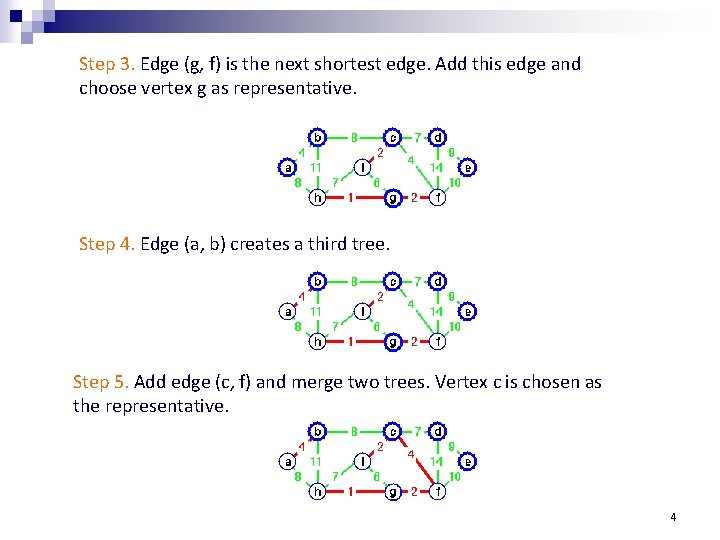
Step 3. Edge (g, f) is the next shortest edge. Add this edge and choose vertex g as representative. Step 4. Edge (a, b) creates a third tree. Step 5. Add edge (c, f) and merge two trees. Vertex c is chosen as the representative. 4

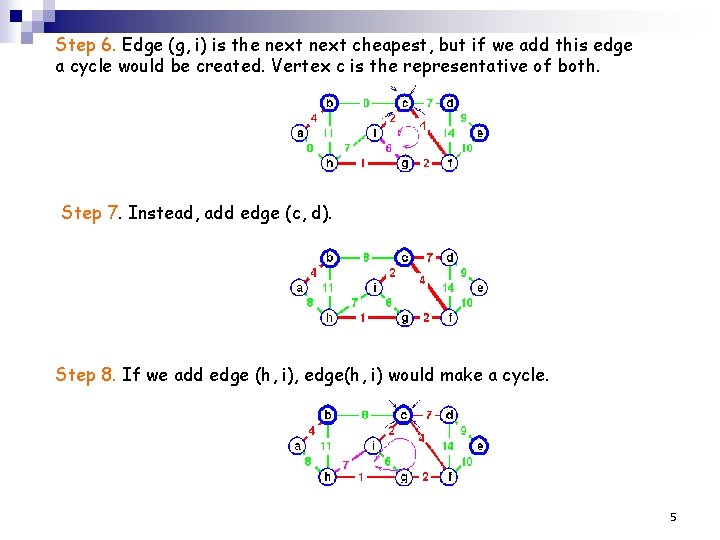
Step 6. Edge (g, i) is the next cheapest, but if we add this edge a cycle would be created. Vertex c is the representative of both. Step 7. Instead, add edge (c, d). Step 8. If we add edge (h, i), edge(h, i) would make a cycle. 5

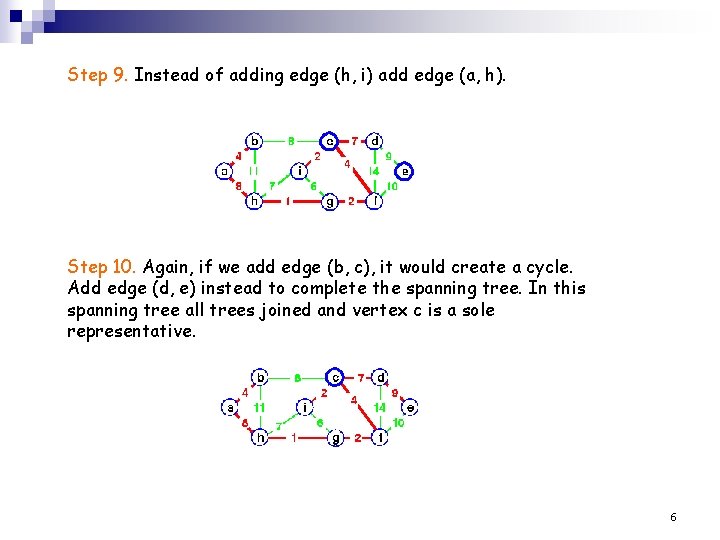
Step 9. Instead of adding edge (h, i) add edge (a, h). Step 10. Again, if we add edge (b, c), it would create a cycle. Add edge (d, e) instead to complete the spanning tree. In this spanning tree all trees joined and vertex c is a sole representative. 6

Dijkstra’s Algorithm v. Dijkstra's algorithm, conceived by Dutch computer scientist Edsger Dijkstra in 1959. v. This algorithm is often used in routing. v. In particular, this algorithm can be used to illustrate the deployment of successive approximation methods by dynamic programming. 7

Dijkstra’s Algorithm ALGORITHM Dijkstra (G, w, s) // Dijkstra’s Algorithm for constructing a minimum spanning tree INITIALIZE SINGLE-SOURCE (G, s) S ← { } // S will ultimately contains vertices of final shortest-path weights from s Initialize priority queue Q i. e. , Q ← V[G] while priority queue Q is not empty do u ← EXTRACT_MIN(Q) // Pull out new vertex S ← S È {u} // Perform relaxation for each vertex v adjacent to u for each vertex v in Adj[u] do Relax (u, v, w) Analysis Dijkstra's algorithm runs in O(|E|lg|V|) time. 8

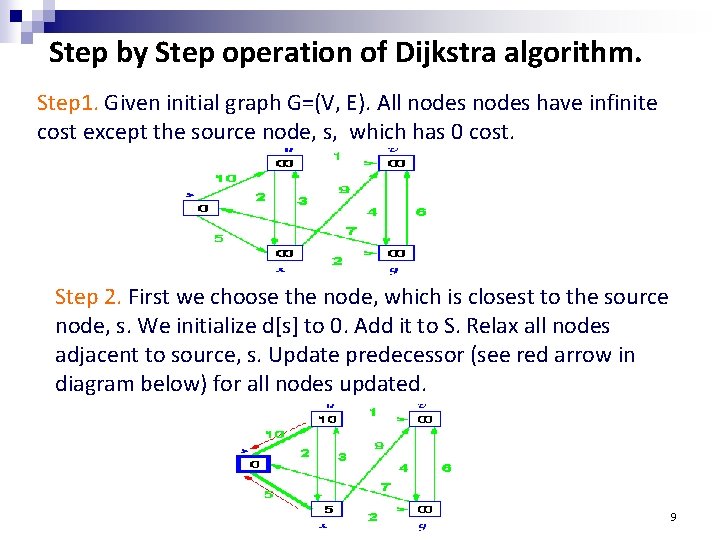
Step by Step operation of Dijkstra algorithm. Step 1. Given initial graph G=(V, E). All nodes have infinite cost except the source node, s, which has 0 cost. Step 2. First we choose the node, which is closest to the source node, s. We initialize d[s] to 0. Add it to S. Relax all nodes adjacent to source, s. Update predecessor (see red arrow in diagram below) for all nodes updated. 9

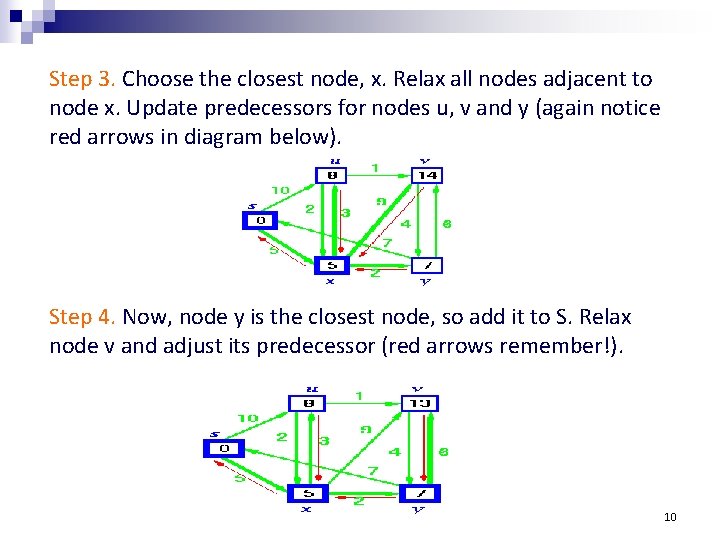
Step 3. Choose the closest node, x. Relax all nodes adjacent to node x. Update predecessors for nodes u, v and y (again notice red arrows in diagram below). Step 4. Now, node y is the closest node, so add it to S. Relax node v and adjust its predecessor (red arrows remember!). 10

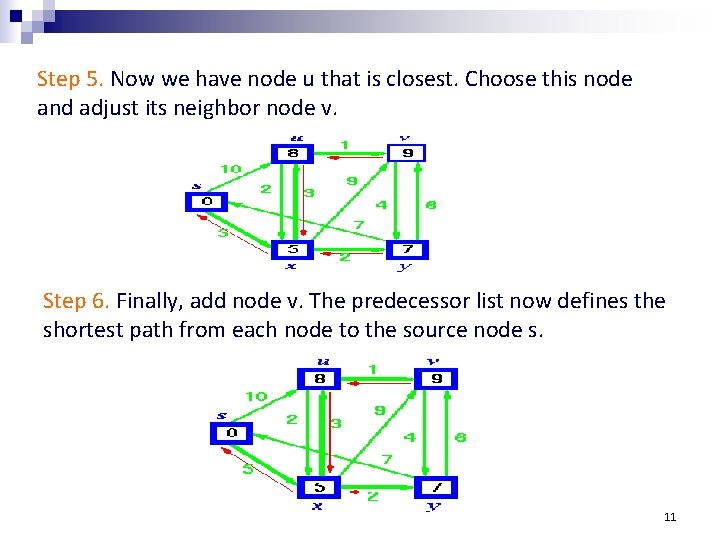
Step 5. Now we have node u that is closest. Choose this node and adjust its neighbor node v. Step 6. Finally, add node v. The predecessor list now defines the shortest path from each node to the source node s. 11

Conclusion o Basically, Kruskal's method is more time-saving (you can order the edges by weight and burn through them fast). o It is a graph search algorithm that solves the single-source shortest path problem for a graph with nonnegative edge path costs, producing a shortest path tree. 12

BIBLIOGRAPHY n n n Dantzig, G. B. (1960), On the shortest path route through a network, Management Science, 6, 187 -190. Dreyfus, S. (1969), An appraisal of some shortest-path algorithms Operations Research, 17, 395 -412. Website : ¨ Microsoft Shortest Path Algorithms Project: research. microsoft. com/research/sv/SPA/ex. html. 13