Krogh Cylinder Steven A Jones BIEN 501 Wednesday

Krogh Cylinder Steven A. Jones BIEN 501 Wednesday, May 7, 2008 Louisiana Tech University Ruston, LA 71272 1

Announcements 1. All homeworks have been assigned. 2. Final exam will be taken from parts of the homework. 3. No homework on Krogh cylinder. 4. Krogh cylinder will not be on the exam. 5. Friday – finish Krogh and do Comparmental Models 6. Monday – Review and Course Evaluations 7. Wednesday - Exam 8. Friday – No class, will be available for questions. 9. Today – Office Hours will start at 10: 30. Louisiana Tech University Ruston, LA 71272 2

Energy Balance Major Learning Objectives: 1. Learn a simple model of capillary transport. Louisiana Tech University Ruston, LA 71272 3

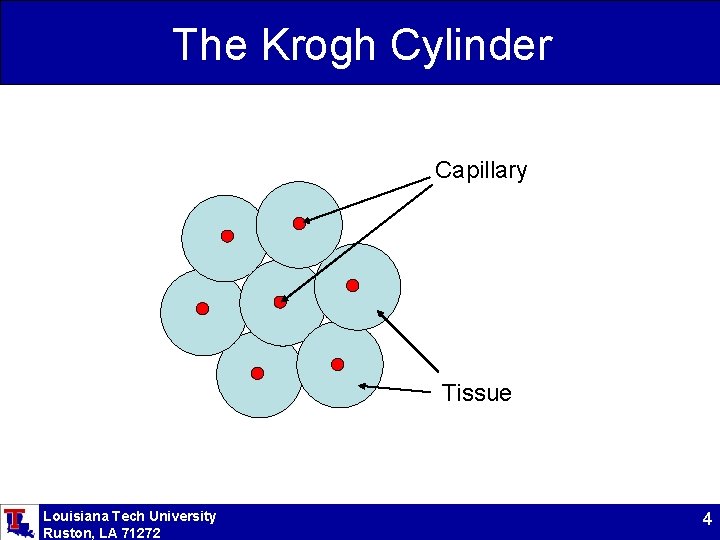
The Krogh Cylinder Capillary Tissue Louisiana Tech University Ruston, LA 71272 4

Assumptions • The geometry follows the Krogh cylinder configuration – Radial symmetry – Transport from capillary – Capillary influences a region of radius Rk. • Reactions are continuously distributed • There is a radial location at which there is no flux Louisiana Tech University Ruston, LA 71272 5

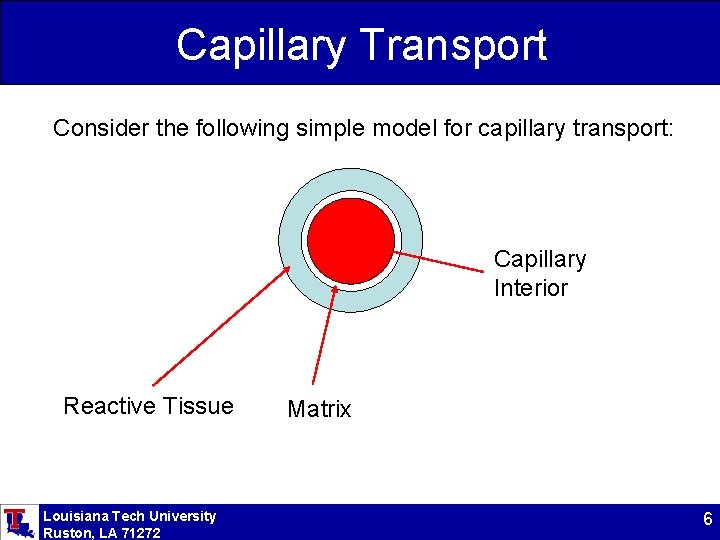
Capillary Transport Consider the following simple model for capillary transport: Capillary Interior Reactive Tissue Louisiana Tech University Ruston, LA 71272 Matrix 6

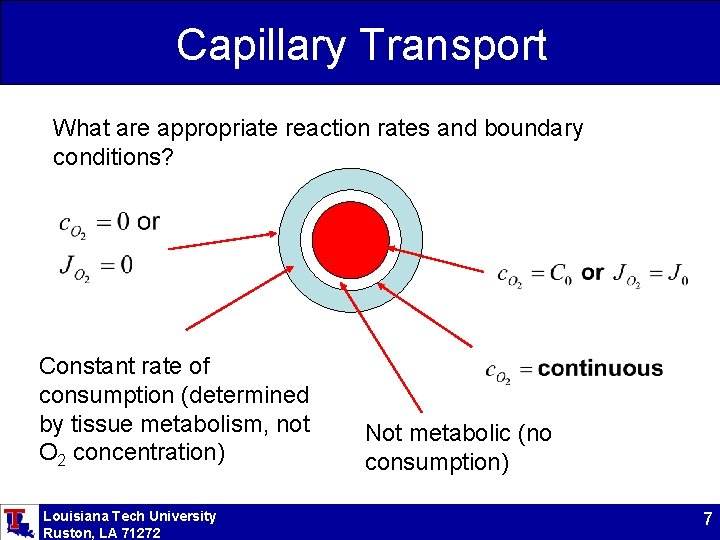
Capillary Transport What are appropriate reaction rates and boundary conditions? Constant rate of consumption (determined by tissue metabolism, not O 2 concentration) Louisiana Tech University Ruston, LA 71272 Not metabolic (no consumption) 7

Diffusion Equation For steady state: Louisiana Tech University Ruston, LA 71272 8

Constant Rate of Reaction Assume the rate of reaction, rx, is constant: (M will be numerially negative since the substance is being consumed). And that the concentration is constant at the capillary wall and zero at the edge of the Krogh cylinder Louisiana Tech University Ruston, LA 71272 9

Constant Reaction: Roadmap The roadmap for solving the steady state problem is as follows: • Integrate the differential equation once to obtain a solution for flux as a function of r. • Use the zero flux boundary condition at Rk to determine the first constant of integration. • Substitute the constant back into the previouslyintegrated differential equation. • Integrate again to obtain the form for concentration. • Use the constant concentration boundary condition to determine the second constant of integration. Louisiana Tech University Ruston, LA 71272 10

First Integration Because there is only one independent variable, : Integrate once: Write in terms of flux: We will use this form to satisfy the no-flux boundary condition at Rk. Louisiana Tech University Ruston, LA 71272 11

Flux Boundary Condition at Rk Since flux is 0 at the edge of the cylinder (Rk), Substitute back into the (once-integrated) differential equation (boxed equation in slide 10): Louisiana Tech University Ruston, LA 71272 12

Second Integration for Concentration With the previous differential equation: Divide by r: Integrate: Louisiana Tech University Ruston, LA 71272 13

Boundary Condition at Capillary Wall From the problem statement (Slide 9) c(Rc) = c 0. Evaluate the previous solution for c(r) at r=Rc. Solve for b. b Louisiana Tech University Ruston, LA 71272 14

Simplify Combine like terms, recalling that : Or, in terms of partial pressures: Louisiana Tech University Ruston, LA 71272 15

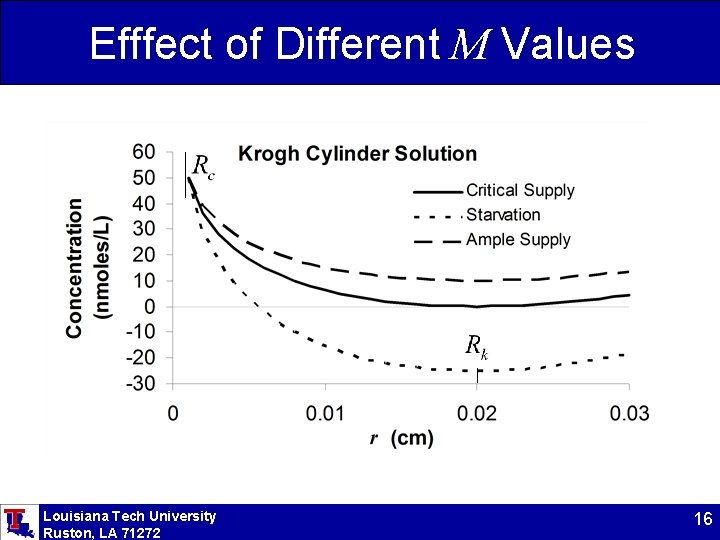
Efffect of Different M Values Louisiana Tech University Ruston, LA 71272 16

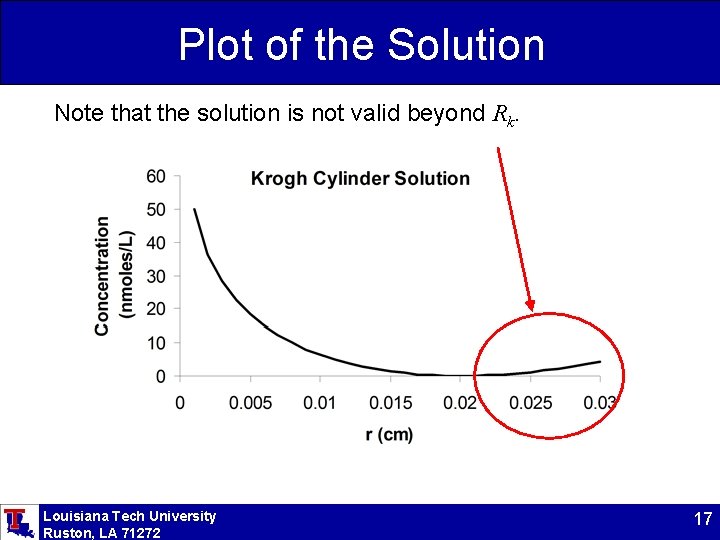
Plot of the Solution Note that the solution is not valid beyond Rk. Louisiana Tech University Ruston, LA 71272 17

Finding Rk The steady state equation is a function of Rk, but an important question is, “What is Rk, given a certain metabolic rate? ” Non-starvation: Halfway between capillaries. Starvation: Is the solution still valid? Louisiana Tech University Ruston, LA 71272 18

Non Steady State Diffusion equation: Initial Condition: Boundary Conditions: Louisiana Tech University Ruston, LA 71272 19

Homogeneous Boundary Conditions The problem will be easier to solve if we can make the boundary conditions homogeneous, i. e. of the form: Our boundary condition at r = rc is not homogeneous because it is in the form: Louisiana Tech University Ruston, LA 71272 20

Homogeneous Boundary Conditions However, if we define the following new variable: The boundary condition at rc becomes: And the boundary condition at rk is still homogeneous: Louisiana Tech University Ruston, LA 71272 21

Non-Dimensionalization The new concentration variable also has the advantage of being dimensionless. We can nondimensionalize the rest of the problem as follows: Let: Why are these forms obvious? The boundary conditions become: The initial condition becomes: Louisiana Tech University Ruston, LA 71272 22

Non-Dimensionalization The diffusion equation can now be non-dimensionalized: Use: So that: Louisiana Tech University Ruston, LA 71272 23

Non-Dimensionalization (Continued) Use: To determine that: Louisiana Tech University Ruston, LA 71272 24

Non-Dimensionalization (Continued) Now apply: To: To get: Louisiana Tech University Ruston, LA 71272 25

Non-Dimensionalization (Cont) Simplify Multiply by Louisiana Tech University Ruston, LA 71272 : 26

Non-Dimensionalization (Cont) Examine The term on the right hand side must be non-dimensional because the left hand side of the equation is non-dimensional. Thus, we have found the correct non-dimensionalization for the reaction rate. Louisiana Tech University Ruston, LA 71272 27

The Mathematical Problem The problem reduces mathematically to: Differential Equation Boundary Conditions Initial Condition Louisiana Tech University Ruston, LA 71272 28

Change to Homogeneous Follow the approach of section 3. 4. 1 (rectangular channel) to change the non-homogeneous equation to a homogeneous equation and a simpler non-homogeneous equation. Diffusion equation: Let: Then: Louisiana Tech University Ruston, LA 71272 29

Divide the Equation The equation is solved if we solve both of the following equations: In other words, we look for a time-dependent part and a time independent (steady state) solution. Note that since the reaction term does not depend on time, it can be satisfied completely by the time-independent term. Louisiana Tech University Ruston, LA 71272 30

Solution to the Spatial Part We already know that the solution to: Is: And that this form satisfies the boundary conditions at rc and rk. It will do so for all time (because it does not depend on time). Louisiana Tech University Ruston, LA 71272 31

Non-Dimensionalize the Spatial Part In terms of the non-dimensional variables: And this form also becomes zero at the two boundaries. Louisiana Tech University Ruston, LA 71272 32

Transient Part We therefore require that: With Boundary Conditions And the Initial Condition Louisiana Tech University Ruston, LA 71272 33

Separation of Variables Homogeneous diffusion equation: Function of t only Louisiana Tech University Ruston, LA 71272 Function of h only 34

The Two ODEs Solutions: What does this equation remind you of? Louisiana Tech University Ruston, LA 71272 35

Radial Dependence Could it perhaps be a zero-order Bessel Function? Louisiana Tech University Ruston, LA 71272 36

Radial Dependence Differential equation for radial dependence becomes: So the solution is: Louisiana Tech University Ruston, LA 71272 37

Radial Dependence This is Bessel’s equation, so the solution is: Louisiana Tech University Ruston, LA 71272 38

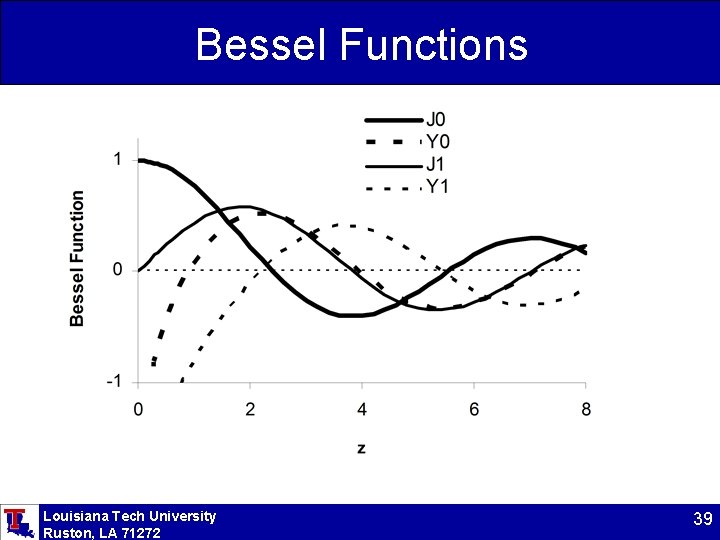
Bessel Functions Louisiana Tech University Ruston, LA 71272 39

Derivatives of Bessel Functions The derivatives of Bessel functions can be obtained from the general relations: Specifically: Louisiana Tech University Ruston, LA 71272 40

Flux Boundary Condition In the solution we will have terms like: We will be requiring the gradient of these terms to go to zero at hk. I. e. The only way these terms can go to zero for all t is if: For every value of l. Louisiana Tech University Ruston, LA 71272 41

Relationship between A and B In other words: And for the boundary condition at the capillary wall: Louisiana Tech University Ruston, LA 71272 42

Characteristic Values We conclude that the allowable values of l are those which satisfy: This is not as simple as previous cases, where the Y 0 term became zero, but it is possible to find these values from Mat. Lab or Excel, given a value for hk. Louisiana Tech University Ruston, LA 71272 43

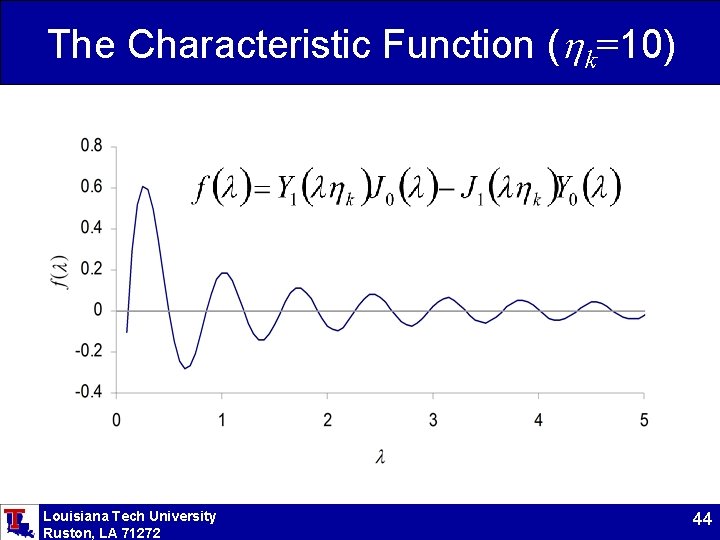
The Characteristic Function (hk=10) Louisiana Tech University Ruston, LA 71272 44

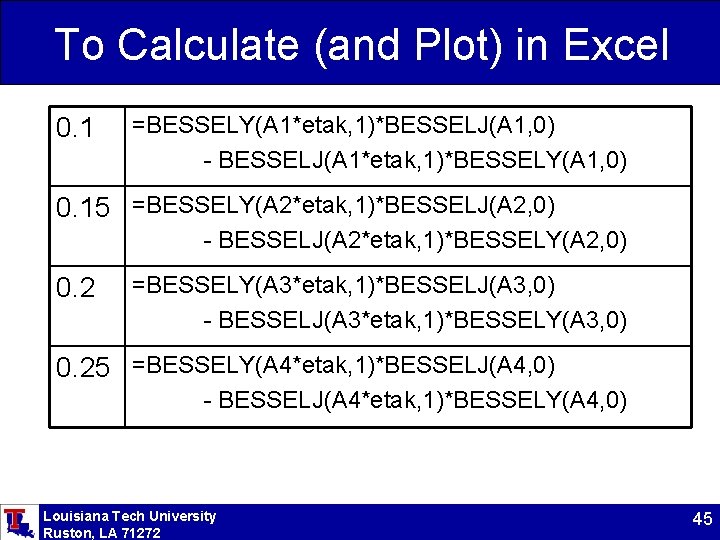
To Calculate (and Plot) in Excel 0. 1 =BESSELY(A 1*etak, 1)*BESSELJ(A 1, 0) - BESSELJ(A 1*etak, 1)*BESSELY(A 1, 0) 0. 15 =BESSELY(A 2*etak, 1)*BESSELJ(A 2, 0) - BESSELJ(A 2*etak, 1)*BESSELY(A 2, 0) 0. 2 =BESSELY(A 3*etak, 1)*BESSELJ(A 3, 0) - BESSELJ(A 3*etak, 1)*BESSELY(A 3, 0) 0. 25 =BESSELY(A 4*etak, 1)*BESSELJ(A 4, 0) - BESSELJ(A 4*etak, 1)*BESSELY(A 4, 0) Louisiana Tech University Ruston, LA 71272 45

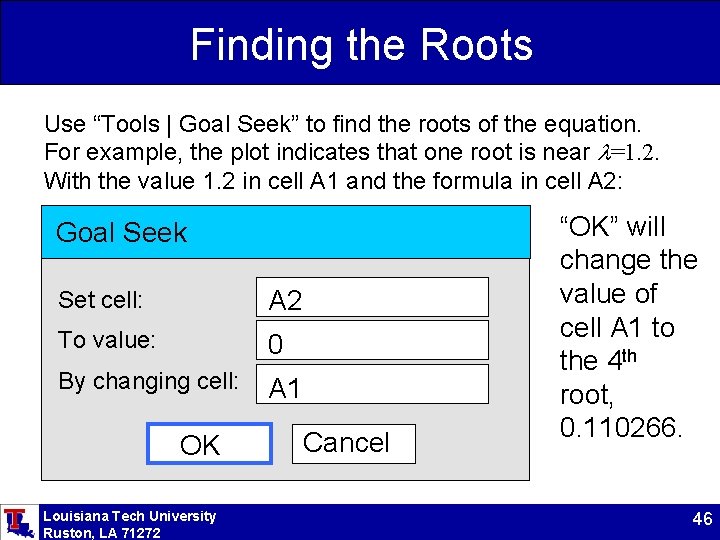
Finding the Roots Use “Tools | Goal Seek” to find the roots of the equation. For example, the plot indicates that one root is near l=1. 2. With the value 1. 2 in cell A 1 and the formula in cell A 2: Goal Seek Set cell: A 2 To value: 0 By changing cell: A 1 OK Louisiana Tech University Ruston, LA 71272 Cancel “OK” will change the value of cell A 1 to the 4 th root, 0. 110266. 46

First Six Roots This process gives the following value for the first 6 roots: Louisiana Tech University Ruston, LA 71272 1 2 3 4 0. 110266 0. 497895 0. 855445 1. 208701 5 6 1. 560322 1. 8 47

Complete Solution The complete solution has the form: Where the values of ln are obtained as described above. Louisiana Tech University Ruston, LA 71272 48

A Prettier Form If we define: We obtain the somewhat more aesthetically pleasing form: Louisiana Tech University Ruston, LA 71272 49

Initial Condition Now apply the initial condition: To: So: Louisiana Tech University Ruston, LA 71272 50

Orthogonality For simplicity, define: These are called “Cylindrical Functions. ” They satisfy the radial Laplacian operator, are zero for h=1, and have zero derivative for h=h. According to the Sturm -Liouville Theorem, the following orthogonality relationship holds for these functions: Louisiana Tech University Ruston, LA 71272 51

Sturm-Liouville Compare: To: Note that h is not the first derivative of h 2, but if we divide by h: and 1 is the 1 st derivative of h Louisiana Tech University Ruston, LA 71272 52

Sturm-Liouville Compare: To: The w(h) is particularly important because it tells us the weighting factor. Louisiana Tech University Ruston, LA 71272 53

Initial Condition With the initial condition: Multiply both sides by Louisiana Tech University Ruston, LA 71272 and integrate: 54

Initial Condition Now use the orthogonality condition: These integrals can be found in tables and worked out to determine the values for the an’s, from which the final answer is obtained. Louisiana Tech University Ruston, LA 71272 55

Fourier Bessel Series For Example: Louisiana Tech University Ruston, LA 71272 56

Integral of Cylindrical Functions To obtain the previous result, take Bessel’s Equation, substituting in the cylindrical function, and multiply by and then integrate. Louisiana Tech University Ruston, LA 71272 57

Norm of Cylindrical Functions For the first term: Integrate by parts with: Louisiana Tech University Ruston, LA 71272 58

Integration by Parts, First Term Louisiana Tech University Ruston, LA 71272 59

Integration by Parts, Second Term The second integral of Slide 54 is: But: So the second integral of Slide 54 is cancels with the last term of I 1, leaving: Louisiana Tech University Ruston, LA 71272 60

Last Term For the last term: Louisiana Tech University Ruston, LA 71272 61

Last Term Louisiana Tech University Ruston, LA 71272 62

Combine the Three Integrals The expression will simplify further, given that we will be working with problems for which either the function or its derivative is zero at each boundary. Louisiana Tech University Ruston, LA 71272 63

What about the similarity solution As it turns out, we did not need to abandon the similarity solution. We could have done the same thing we did with the separation of variables solution. I. e. we could have said that the complete solution is the sum of the particular solution and a sum of similarity solutions. Louisiana Tech University Ruston, LA 71272 64

Louisiana Tech University Ruston, LA 71272 65

Similarity Solution? We could attempt a similarity solution: Which transforms the equation to: Louisiana Tech University Ruston, LA 71272 66

Transform Variables From Previous: Multiply by r 2/D Louisiana Tech University Ruston, LA 71272 67

The Problem From Previous: If this had been a “no reaction” problem, the method would work. Unfortunately, the reaction term prevents the similarity solution from working, so we need to take another approach. Louisiana Tech University Ruston, LA 71272 68