KripkeStyle Semantics for Normal Systems Arnon Avron and

Kripke-Style Semantics for Normal Systems Arnon Avron and Ori Lahav Tel Aviv University LATD 2010

Normal Gentzen Systems �Fully-structural propositional sequential systems �Normal derivation rule: ◦ The rule: s 1 s 2 … sm / c ◦ Its application: (s 1)+context 1 … (sm)+contextm (c)+context 3

Normal Rules �Example p 1 p 2 / p 1 p 2 , φ , ψ , φ ψ φ ψ 4

Normal Rules �Example p 1 p 2 / p 1 p 2 wff , φ , ψ , φ ψ φ ψ �Each premise is associated with a context restriction. 5

Many-Sided Sequents � Classical sequent: ( , are finite sets of formulas) � n-sided sequent: 1 ; 2 ; … ; n � Notation ◦ Let I be a finite set of signs. ◦ A signed formula: i ψ (i I and ψ is a formula). ◦ A sequent is a finite set of signed formulas. � Negative interpretation [Baaz, Fermüller, Zach `93] {i 1 ψ1, …, in ψn} is true iff ik is not the truth-value assigned to ψk for some i k n � Classical sequent notation is I = {t, f} { t ψ | ψ } { f ψ | ψ } 6

Normal Rules �A normal rule: ◦ Premises: sequents s 1 … sm ◦ Context restrictions: corresponding sets of signed formulas 1 … m ◦ A Conclusion: a sequent c �Its application: (s 1) (s’ 1) … (sm) (s’ m) (c) s’ 7

Examples �S 4’s Box , ψ I = {t, f} p 1 , / p 1 ={t φ|φ wff } {f φ|φ wff } � 3 -Valued , ψ Lukasiewicz's Implication [Zach `93] I = {f, I, t} f p 1 , , I p 1, I p 2 , , t p 2 , / t p 1 p 2 ={ i φ | i I , φ wff } (i. e. no context restriction) , φ; ; Σ ; , φ, ψ; Σ ; ; Σ, ψ ; ; Σ, φ ψ 8

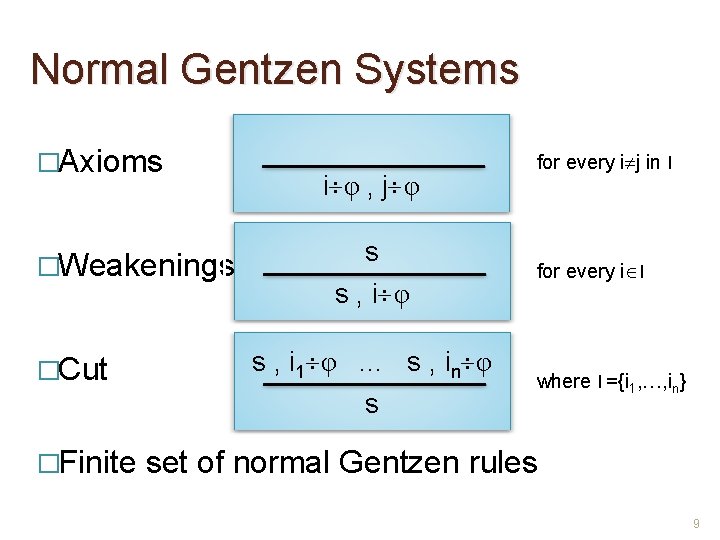
Normal Gentzen Systems �Axioms �Weakenings �Cut i φ , j φ s s , i φ s , i 1 φ … s , in φ s �Finite for every i j in I for every i I where I ={i 1, …, in} set of normal Gentzen rules 9

Examples of Normal Gentzen Systems �Normal Gentzen systems are suitable for: ◦ ◦ ◦ ◦ Classical logic Intuitionistic logic Dual-intuitionistic logic Bi-intuitionistic logic S 4 and S 5 n-valued Lukasiewicz logic … 10

Kripke Semantics �Kripke Frame ◦ Set of worlds W ◦ Legal set of relations R 1, R 2, … W W ◦ Legal valuation v : W x wff I sequent s is true in a W iff i φ s. v(a, φ) i �A sequent is R-true in a W iff it is true in every b W s. t. a. Rb �A 11

G-Legal Kripke Frames �A normal system G induces a set of G-legal Kripke frames: ◦ A preorder R for every context-restriction in G. �If is the set of all signed formulas, R is the identity relation ◦ Generalized persistence condition If i φ , v(a, φ)=i implies v(b, φ)=i for every b s. t. a. R b. ◦ The valuation should respect the logical rules of G Respect a rule s 1, 1 , …, sm, m / c : If 1 i m. σ(si) is R i-true in a W, then σ(c) is true in a 12

Example: Primal Intuitionistic Implication (Gurevich ‘ 09) �Rules 1 2 p 2 , wff / p 1 p 2 p 1, wff , p 2 , wff / p 1 p 2 �Semantics , , , = Rwff Persistence if v(a, )=t then v(b, )=t for every b a Respect rule #1 v(a, )=t if v(b, )=t for every b a Respect rule #2 v(a, )=f if v(a, )=t and v(a, )=f ◦ v(a, ) is free when v(a, )=f and (v(b, )=f or v(b, )=t for every b a) 13

Strong Soundness and Completeness �For every normal system G, C├G s iff every G-legal frame which is a model of C is also a model of s. �Applications: ◦ Several known completeness theorems are immediately obtained as special cases. ◦ Compactness theorem. ◦ Basis for semantic proofs of analycity. ◦ Semantic decision procedure for analytic systems. 14

Analycity �A normal system is (strongly) analytic iff it has the subformula property, i. e. C├G s implies that there exists a proof of s from C in G that contains only subformulas of C and s. �Analycity implies: decidability, consistency and conservativity. 15

Semantic Characterization of Analycity � Def Given a set E of formulas, an E-Semiframe is a Kripke frame, except for: v : W E I instead of v : W wff I. � Notation Given a set E of formulas, C├Es. G iff there exists a proof of s from C in G containing only formulas from E. � Thm C├Es. G iff every G-legal E-semiframe which is a model of C is also a model of s. � Cor G is analytic iff for every C and s, if every G-legal frame which is a model of C is also a model of s, then this is also true with respect to sub[C, s]-semiframes. 16

Semantic Proofs of Analycity To prove that G is analytic, it suffices to prove: � Every G-legal semiframe can be G-legal frame. extended to a This can be easily done in many important cases: � ◦ ◦ Normal systems for classical logic, intuitionistic logic, dual and bi-intuitionistic logics, S 4, S 5, nvalued Lukasiewicz's logic… The family of coherent canonical systems. 17

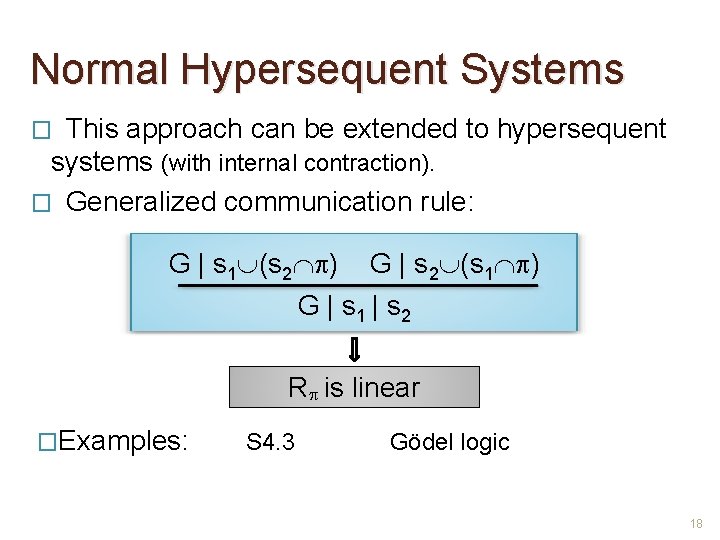
Normal Hypersequent Systems This approach can be extended to hypersequent systems (with internal contraction). � Generalized communication rule: � G | s 1 (s 2 ) G | s 2 (s 1 ) G | s 1 | s 2 R is linear �Examples: S 4. 3 Gödel logic 18

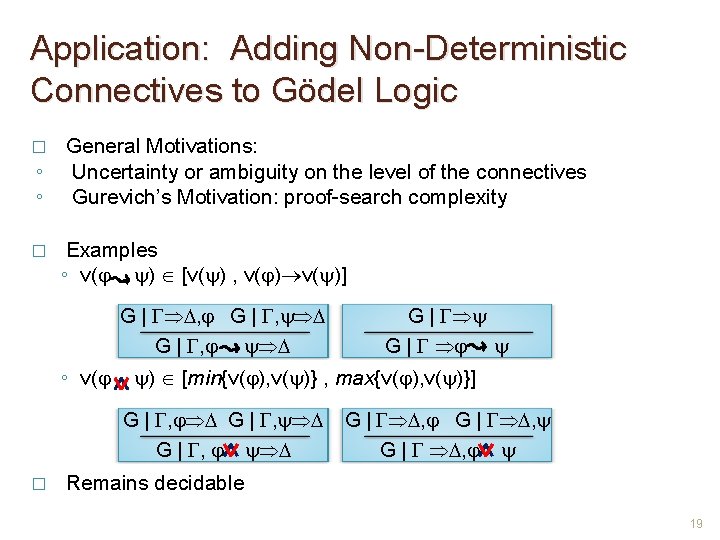
Application: Adding Non-Deterministic Connectives to Gödel Logic � ◦ ◦ � General Motivations: Uncertainty or ambiguity on the level of the connectives Gurevich’s Motivation: proof-search complexity Examples ◦ v( ) [v( ) , v( )] G | , G | , ◦ v( ) [min{v( ), v( )} , max{v( ), v( )}] G | , � G | , G | , Remains decidable 19

Thank you! 20