Kriging Introduction Method invented in the 1950 s

Kriging - Introduction • Method invented in the 1950 s by South African geologist Daniel Krige (1919 -) for predicting distribution of minerals. • Became very popular for fitting surrogates to expensive computer simulations in the 21 st century. • It is one of the best surrogates available. • It probably became popular late mostly because of the high computer cost of fitting it to data.

Kriging philosophy • We assume that the data is sampled from an unknown function that obeys simple correlation rules. • The value of the function at a point is correlated to the values at neighboring points based on their separation in different directions. • The correlation is strong to nearby points and weak with far away points, but strength does not change based on location. • Normally Kriging is used with the assumption that there is no noise so that it interpolates exactly the function values. • It works out to be a local surrogate, and it uses functions that are very similar to radial basis functions.

Reminder: Covariance and Correlation • Covariance of two random variables X and Y • The covariance of a random variable with itself is the square of the standard deviation • Covariance matrix for a vector contains the covariances of the components • Correlation • The correlation matrix has 1 on the diagonal.

Correlation between function values at nearby points for sine(x) • Generate 10 random numbers, translate them by a bit (0. 1), and by more (1. 0) x=10*rand(1, 10) 8. 147 9. 058 1. 267 9. 134 6. 324 0. 975 2. 785 5. 469 9. 575 9. 649 xnear=x+0. 1; xfar=x+1; • Calculate the sine function at the three sets. ynear=sin(xnear) 0. 9237 0. 2637 0. 9799 0. 1899 0. 1399 0. 8798 0. 2538 -0. 6551 -0. 2477 -0. 3185 y=sin(x) 0. 9573 0. 3587 0. 9551 0. 2869 0. 0404 0. 8279 0. 3491 -0. 7273 -0. 1497 -0. 2222 yfar=sin(xfar) 0. 2740 -0. 5917 0. 7654 -0. 6511 0. 8626 0. 9193 -0. 5999 0. 1846 -0. 9129 -0. 9405 • Compare corelations. r=corrcoef(y, ynear) 0. 9894; rfar=corrcoef(y, yfar) 0. 4229 • Decay to about 0. 4 over one sixth of the wavelength.

Gaussian correlation function •

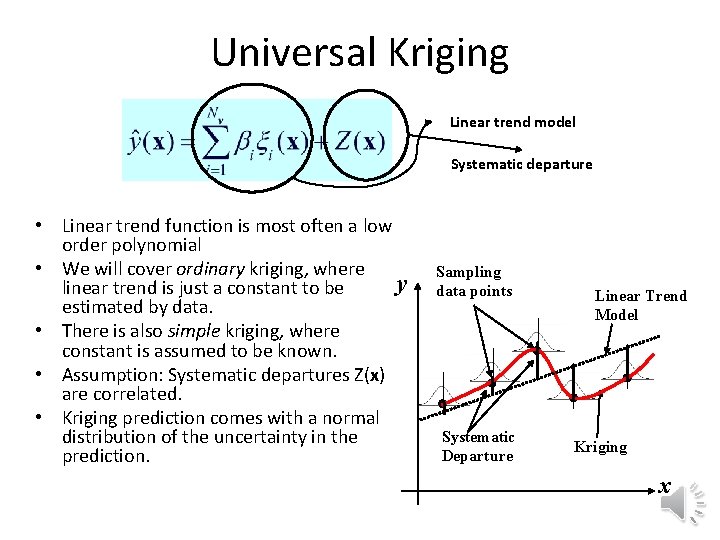
Universal Kriging Linear trend model Systematic departure • Linear trend function is most often a low order polynomial • We will cover ordinary kriging, where y linear trend is just a constant to be estimated by data. • There is also simple kriging, where constant is assumed to be known. • Assumption: Systematic departures Z(x) are correlated. • Kriging prediction comes with a normal distribution of the uncertainty in the prediction. Sampling data points Systematic Departure Linear Trend Model Kriging x

Notation •

Prediction and shape functions •

Fitting the data •

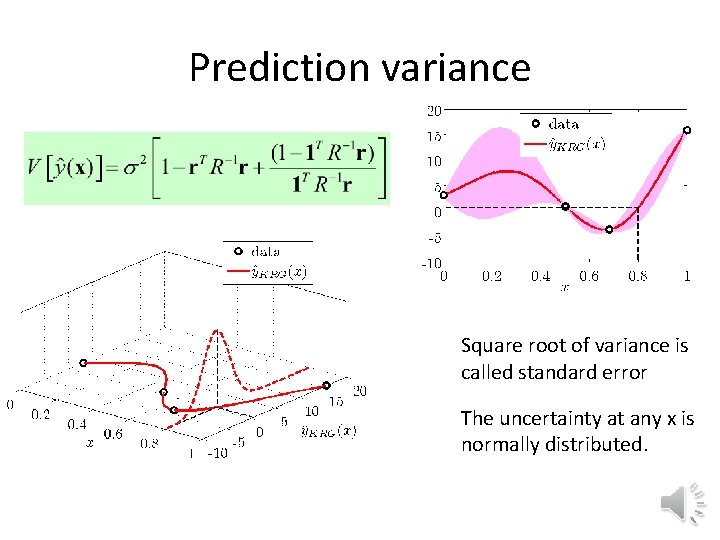
Prediction variance Square root of variance is called standard error The uncertainty at any x is normally distributed.

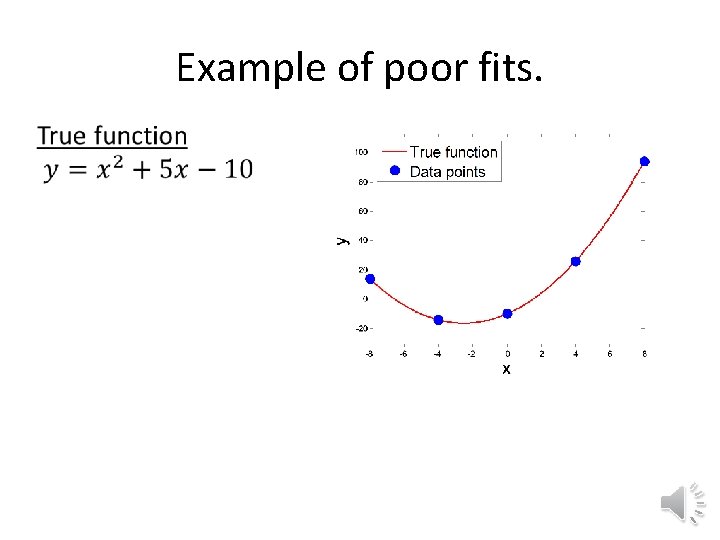
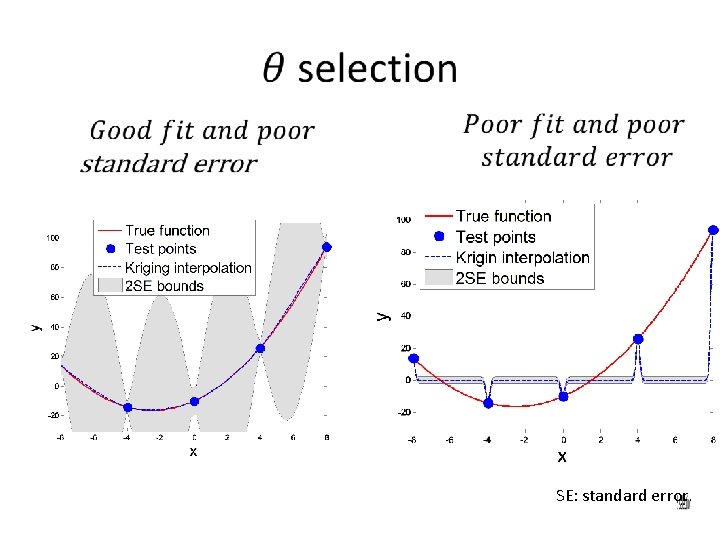
Kriging fitting problems • The maximum likelihood or cross-validation optimization problem solved to obtain the kriging fit is often ill-conditioned leading to poor fit, or poor estimate of the prediction variance. • Poor estimate of the prediction variance can be checked by comparing it to the cross validation error. • Poor fits are often characterized by the kriging surrogate having large curvature near data points (see example on next slide). • It is recommended to visualize by plotting the kriging fit and its standard error.

Example of poor fits.

SE: standard error

Problems • Fit the quadratic function of Slide 13 with kriging using different options, like different covariance and trend function and compare the accuracy of the fit. • For this problems compare the standard error with the actual error.