Kramers a k a Cramers Rule Component j

Kramer’s (a. k. a Cramer’s) Rule • Component j of x = A-1 b is • Form Bj by replacing column j of A with b.

Total Unimodularity • A square, integer matrix B is unimodular (UM) if its determinant is 1 or -1. • An integer matrix A is called totally unimodular (TUM) if every square, nonsingular submatrix of A is UM. • From Cramer’s rule, it follows that if A is TUM and b is an integer vector, then every BFS of the constraint system Ax = b is integer.

TUM Theorem • An integer matrix A is TUM if – All entries are -1, 0 or 1 – At most two non-zero entries appear in any column – The rows of A can be partitioned into two disjoint sets such that • If a column has two entries of the same sign, their rows are in different sets. • If a column has two entries of different signs, their rows are in the same set. • The MCNFP constraint matrices are TUM.

General Form of the MCNF Problem

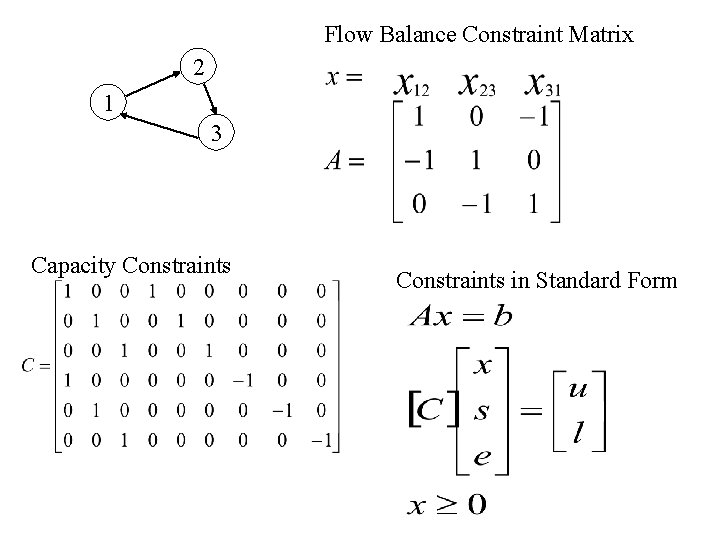
Flow Balance Constraint Matrix 2 1 3 Capacity Constraints in Standard Form

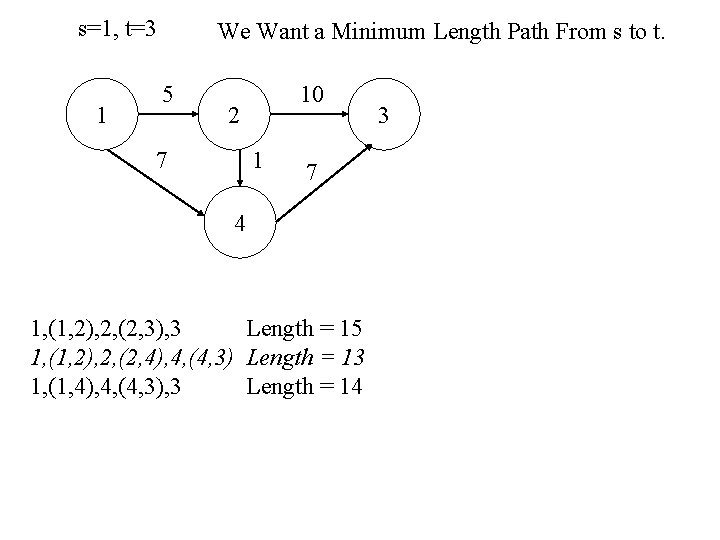
Shortest Path Problems • Defined on a Network – Nodes, Arcs and Arc Costs – Two Special Nodes • Origin Node s • Destination Node t • A path from s to t is an alternating sequence of nodes and arcs starting at s and ending at t: s, (s, v 1), v 1, (v 1, v 2), …, (vi, vj), vj, (vj, t), t

s=1, t=3 1 We Want a Minimum Length Path From s to t. 5 10 2 7 1 7 4 1, (1, 2), 2, (2, 3), 3 Length = 15 1, (1, 2), 2, (2, 4), 4, (4, 3) Length = 13 1, (1, 4), 4, (4, 3), 3 Length = 14 3

Maximizing Rent Example • Optimally Select Non-Overlapping Bids for 10 periods

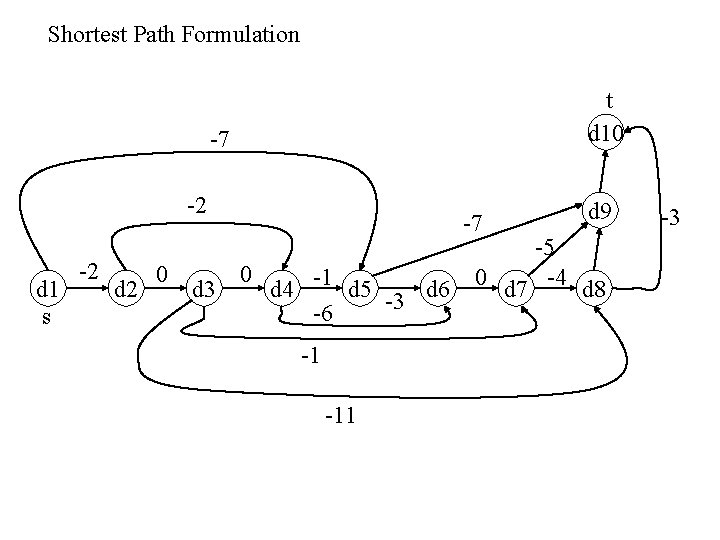
Shortest Path Formulation t d 10 -7 -2 d 1 s -2 d 2 0 d 3 -7 0 d 4 -1 d 5 d 6 -3 -6 -1 -11 d 9 -5 0 d 7 -4 d 8 -3

MCNF Formulation of Shortest Path Problems • • • Origin Node s has a supply of 1 Destination Node t has a demand of 1 All other Nodes are Transshipment Nodes Each Arc has Capacity 1 Tracing A Unit of Flow from s to t gives a Path from s to t

Maximum Flow Problems • Defined on a Network – Source Node s – Sink Node t – All Other Nodes are Transshipment Nodes – Arcs have Capacities, but no Costs • Maximize the Flow from s to t

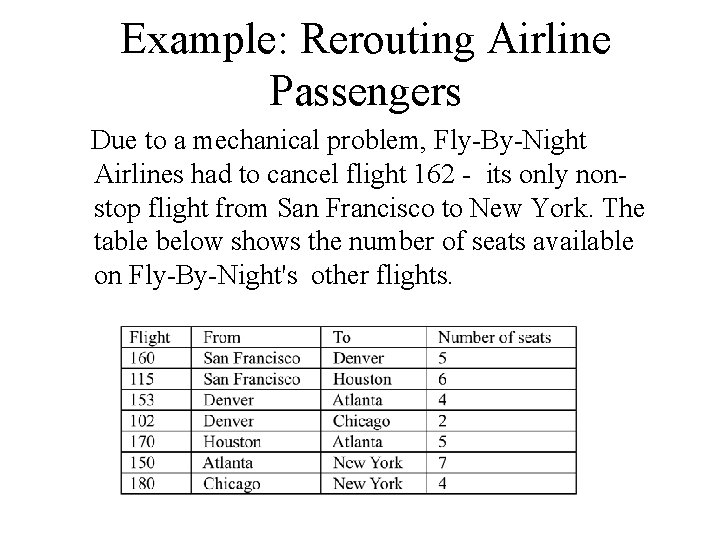
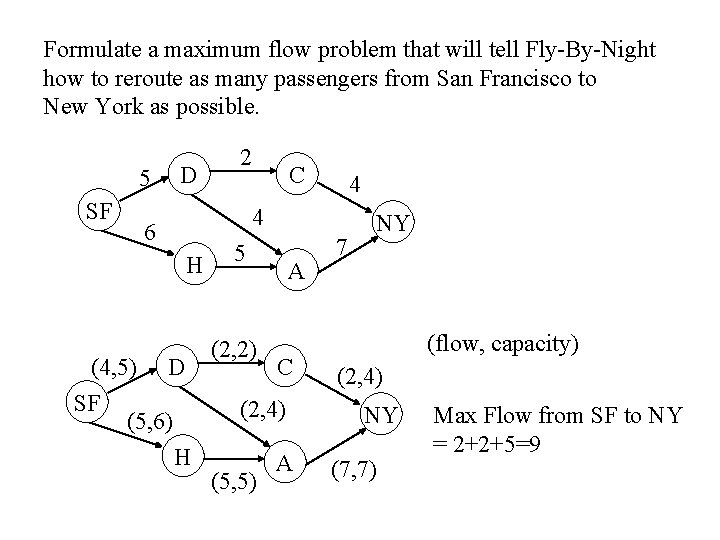
Example: Rerouting Airline Passengers Due to a mechanical problem, Fly-By-Night Airlines had to cancel flight 162 - its only nonstop flight from San Francisco to New York. The table below shows the number of seats available on Fly-By-Night's other flights.

Formulate a maximum flow problem that will tell Fly-By-Night how to reroute as many passengers from San Francisco to New York as possible. 5 SF D 2 C 4 4 6 H (4, 5) D SF (5, 6) H 5 (2, 2) A C (2, 4) (5, 5) A 7 NY (flow, capacity) (2, 4) NY (7, 7) Max Flow from SF to NY = 2+2+5=9

MCNF Formulation of Maximum Flow Problems • Let Arc Cost = 0 for all Arcs • Add an infinite capacity arc from t to s – Give this arc a cost of -1

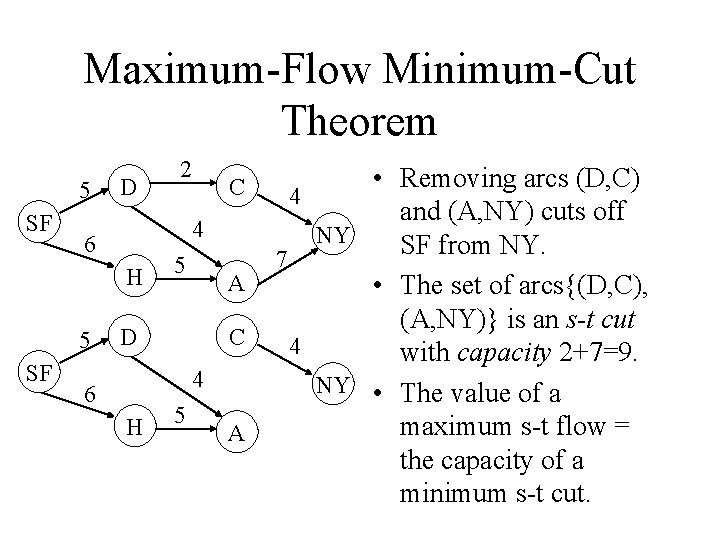
Maximum-Flow Minimum-Cut Theorem 5 SF D H SF C 4 6 5 2 5 A D C 4 6 H 5 A • Removing arcs (D, C) 4 and (A, NY) cuts off NY SF from NY. 7 • The set of arcs{(D, C), (A, NY)} is an s-t cut 4 with capacity 2+7=9. NY • The value of a maximum s-t flow = the capacity of a minimum s-t cut.