Korea University How to Implement 3 D Graphics

Korea University How to Implement 3 D Graphics Applications Jung Lee, airjung@korea. ac. kr Computer Graphics Laboratory

Korea University In This Class n Draw a 3 D scene on the screen n n Orthographic and perspective Necessary operations n Backface culling n n n 3 D clipping Depth calculation n n Inner product between view direction and normal vectors Determines which object is closer to the eye position Scan conversion n After projecting all visible objects on the view plane Jung Lee, airjung@korea. ac. kr 2 Computer Graphics Laboratory

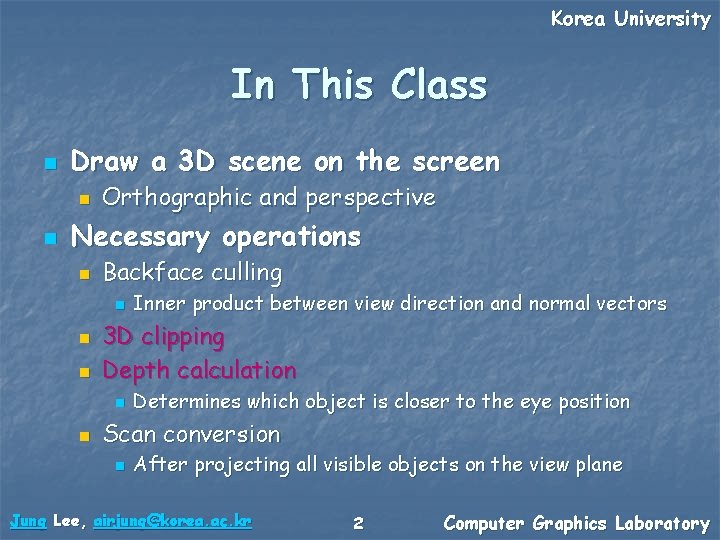
Korea University 3 D Clipping n For the objects outside the side planes n n n Just project them onto the view plane 2 D polygon/line clipping using the projected shapes For the objects outside the near/far planes n Investigate all the lines of each object n n Case of fully outside: clipped Case of intersection n Intersecting points will be used for projection Jung Lee, airjung@korea. ac. kr 3 Computer Graphics Laboratory

Korea University 3 D Clipping Example Far Plane : Intersecting Points Near Plane View Window <Orthographic Projection> Jung Lee, airjung@korea. ac. kr 4 Computer Graphics Laboratory

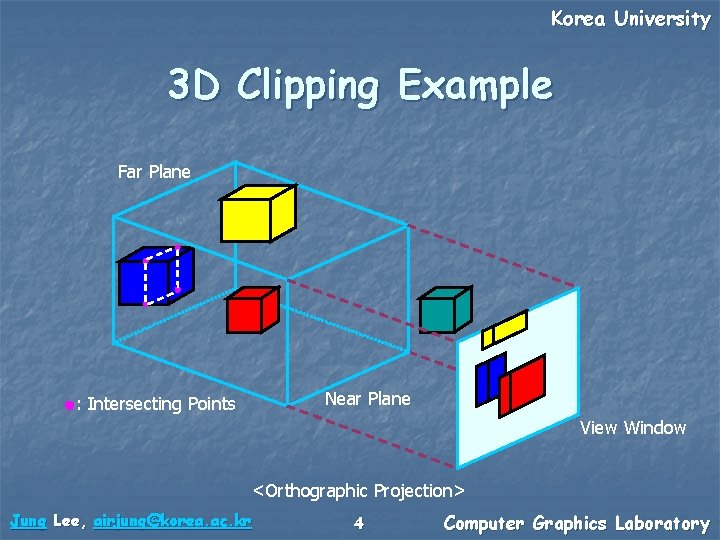
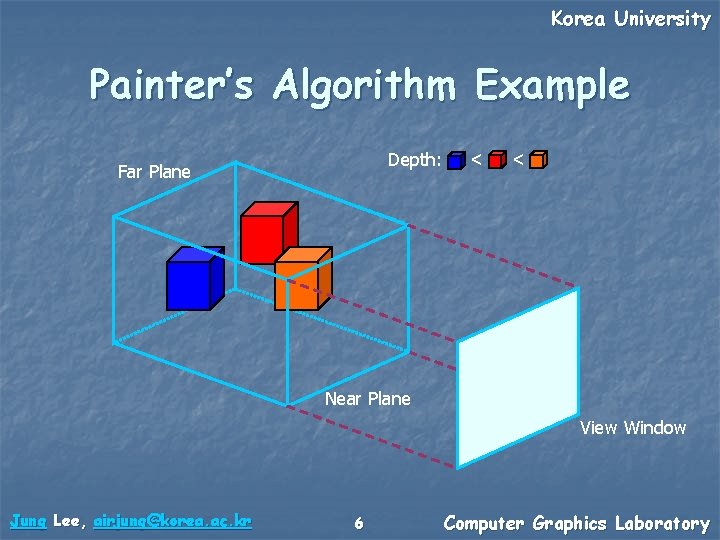
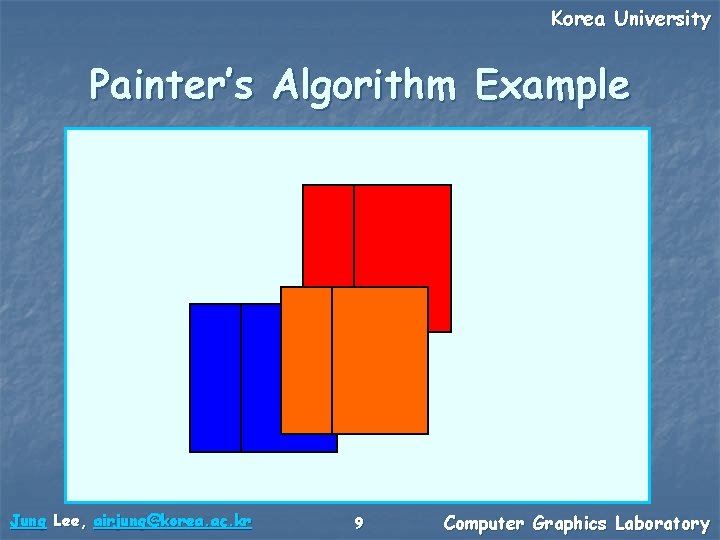
Korea University Depth Sorting n Painter’s algorithm n n Draw the farther objects first The simplest way The closer object overrides the farther one Problem n n In the case of concave objects Depth buffer n n Robust way Store the depth of the drawn pixels Jung Lee, airjung@korea. ac. kr 5 Computer Graphics Laboratory

Korea University Painter’s Algorithm Example Depth: Far Plane < < Near Plane View Window Jung Lee, airjung@korea. ac. kr 6 Computer Graphics Laboratory

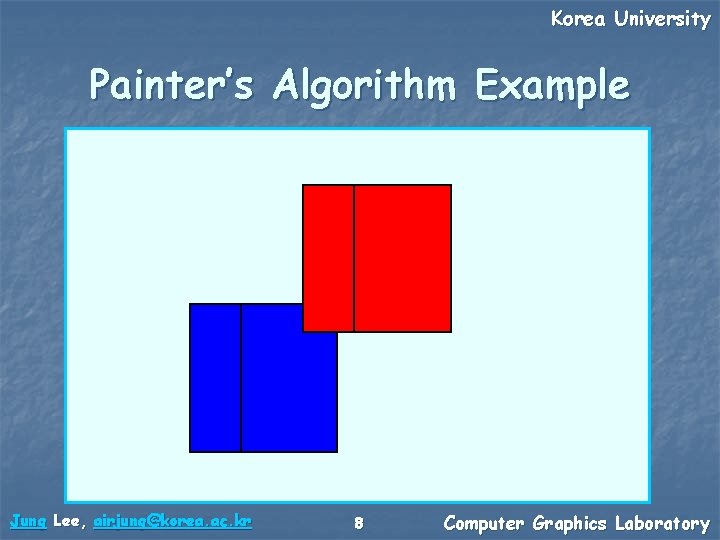
Korea University Painter’s Algorithm Example Jung Lee, airjung@korea. ac. kr 7 Computer Graphics Laboratory

Korea University Painter’s Algorithm Example Jung Lee, airjung@korea. ac. kr 8 Computer Graphics Laboratory

Korea University Painter’s Algorithm Example Jung Lee, airjung@korea. ac. kr 9 Computer Graphics Laboratory

Korea University Basic Data Types n For rendering n Point (Vertex) n n Can be represented as a vector Polygon usually triangle n n n Consists of n vertices (n: # of its member points) Connectivity information To transform/draw a triangle n n Transform/draw its member lines bottom-up Common attributes n n Color Normal vector Jung Lee, airjung@korea. ac. kr 10 Computer Graphics Laboratory

Korea University Basic Data Types n For transformation n Vector n n 4 x 1 for homogeneous coordinate system Inner product Cross product Matrix n n n 4 x 4 for homogeneous coordinate system Multiplication Translation, rotation, scaling matrices Jung Lee, airjung@korea. ac. kr 11 Computer Graphics Laboratory

Korea University VECTOR Class class VECTOR { void Add(VECTOR v); void Subtract(VECTOR v); VECTOR Cross. Product(VECTOR v); float Inner. Product(VECTOR v); float dir[4]; }; Jung Lee, airjung@korea. ac. kr 12 Computer Graphics Laboratory

Korea University VECTOR Method void VECTOR: : Add(VECTOR v) { for(int i=0; i<4; i++) dir[i] += v. dir[i]; } void VECTOR: : Subtract(VECTOR v) { for(int i=0; i<4; i++) dir[i] -= v. dir[i]; } Jung Lee, airjung@korea. ac. kr 13 Computer Graphics Laboratory

Korea University VECTOR Method VECTOR: : Cross. Product(VECTOR v) { VECTOR result; result. dir[0] result. dir[1] result. dir[2] result. dir[3] = = dir[1] * v. dir[2] - dir[2] * v. dir[1]; dir[2] * v. dir[0] - dir[0] * v. dir[2]; dir[0] * v. dir[1] - dir[1] * v. dir[0]; 1; return result; } Jung Lee, airjung@korea. ac. kr 14 Computer Graphics Laboratory

Korea University VECTOR Method float VECTOR: : Inner. Product(VECTOR v) { float result; result = dir[0] * v. dir[0] + dir[1] * v. dir[1] + dir[2] * v. dir[2]; return result; } Jung Lee, airjung@korea. ac. kr 15 Computer Graphics Laboratory

Korea University LINE class LINE { VECTOR head; VECTOR tail; }; Jung Lee, airjung@korea. ac. kr 16 Computer Graphics Laboratory

Korea University TRIANGLE Class class TRIANGLE { LINE e 1; // edges LINE e 2; // edges LINE e 3; // edges char rgb[3]; // color VECTOR normal; // normal vector }; Jung Lee, airjung@korea. ac. kr 17 Computer Graphics Laboratory

Korea University MATRIX Class class MATRIX { MATRIX Multiply(MATRIX m); VECTOR Multiply(VECTOR v); void Createfrom. Elements(float *e); void Trans(float tx, float ty, float tz); void Scale(float sx, float sy, float sz); void Rotate. X(float angle); void Rotate. Y(float angle); void Rotate. Z(float angle); float element[4][4]; }; Jung Lee, airjung@korea. ac. kr 18 Computer Graphics Laboratory

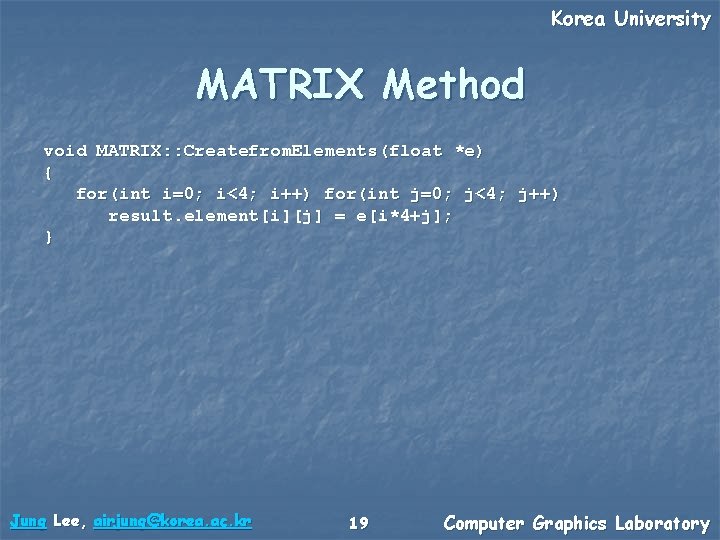
Korea University MATRIX Method void MATRIX: : Createfrom. Elements(float *e) { for(int i=0; i<4; i++) for(int j=0; j<4; j++) result. element[i][j] = e[i*4+j]; } Jung Lee, airjung@korea. ac. kr 19 Computer Graphics Laboratory

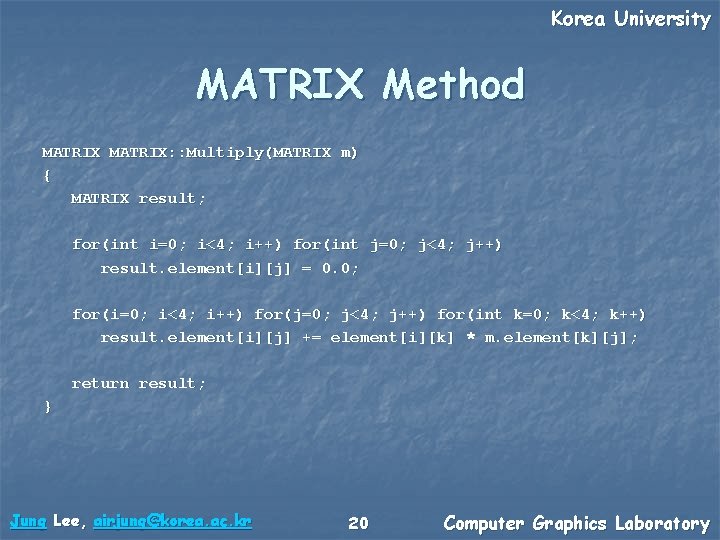
Korea University MATRIX Method MATRIX: : Multiply(MATRIX m) { MATRIX result; for(int i=0; i<4; i++) for(int j=0; j<4; j++) result. element[i][j] = 0. 0; for(i=0; i<4; i++) for(j=0; j<4; j++) for(int k=0; k<4; k++) result. element[i][j] += element[i][k] * m. element[k][j]; return result; } Jung Lee, airjung@korea. ac. kr 20 Computer Graphics Laboratory

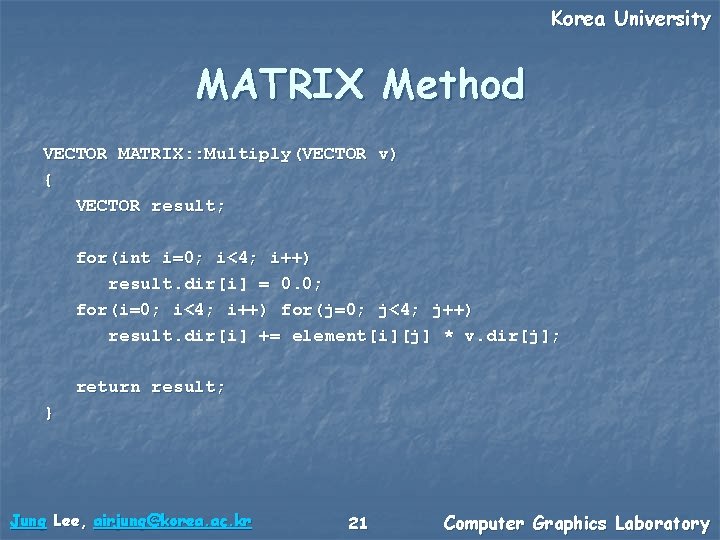
Korea University MATRIX Method VECTOR MATRIX: : Multiply(VECTOR v) { VECTOR result; for(int i=0; i<4; i++) result. dir[i] = 0. 0; for(i=0; i<4; i++) for(j=0; j<4; j++) result. dir[i] += element[i][j] * v. dir[j]; return result; } Jung Lee, airjung@korea. ac. kr 21 Computer Graphics Laboratory

Korea University MATRIX Method void MATRIX: : Trans(float tx, float ty, float tz) { for(int i=0; i<4; i++) for(int j=0; j<4; j++) element[i][j] = 0. 0; element[0][0] element[1][1] element[2][2] element[3][3] = = 1. 0; element[0][3] = tx; 1. 0; element[1][3] = ty; 1. 0; element[2][3] = tz; 1. 0; } Jung Lee, airjung@korea. ac. kr 22 Computer Graphics Laboratory

Korea University MATRIX Method void MATRIX: : Scale(float sx, float sy, float sz) { for(int i=0; i<4; i++) for(int j=0; j<4; j++) element[i][j] = 0. 0; element[0][0] = sx; element[1][1] = sy; element[2][2] = sz; element[3][3] = 1. 0; } Jung Lee, airjung@korea. ac. kr 23 Computer Graphics Laboratory

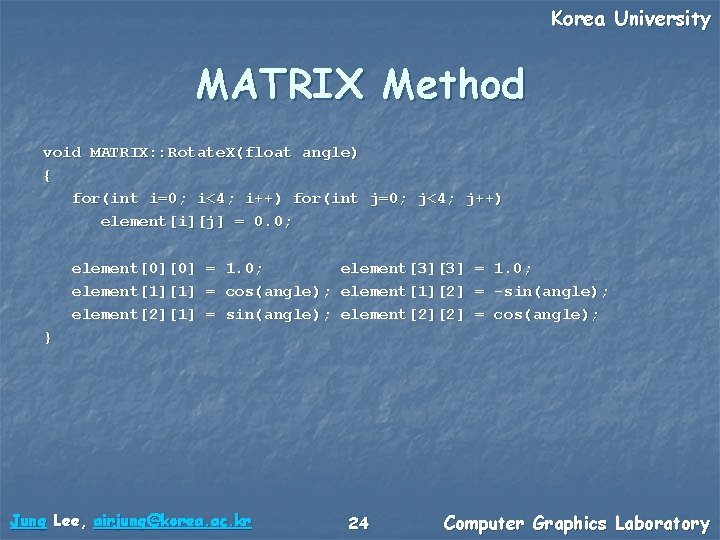
Korea University MATRIX Method void MATRIX: : Rotate. X(float angle) { for(int i=0; i<4; i++) for(int j=0; j<4; j++) element[i][j] = 0. 0; element[0][0] element[1][1] element[2][1] = = = 1. 0; cos(angle); sin(angle); element[3][3] element[1][2] element[2][2] = = = 1. 0; -sin(angle); cos(angle); } Jung Lee, airjung@korea. ac. kr 24 Computer Graphics Laboratory

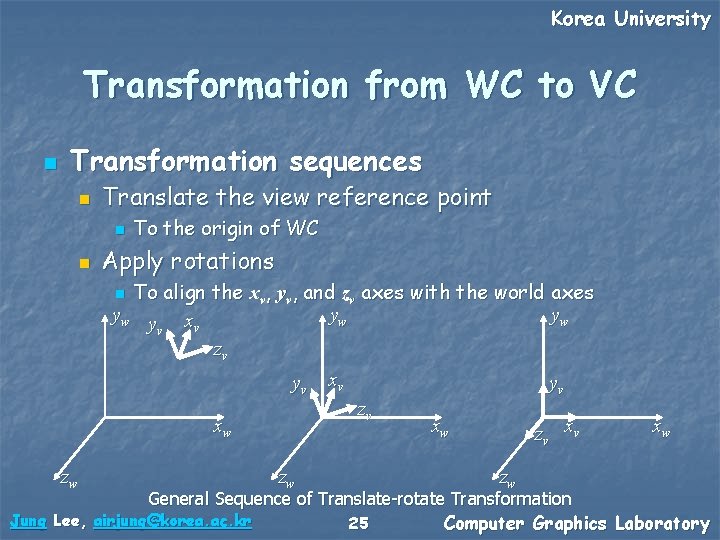
Korea University Transformation from WC to VC n Transformation sequences n Translate the view reference point n n To the origin of WC Apply rotations To align the xv, yv, and zv axes with the world axes yw y x yw yw v v zv n yv xw zw zw xv zv yv zv x v xw zw xw General Sequence of Translate-rotate Transformation Jung Lee, airjung@korea. ac. kr 25 Computer Graphics Laboratory

Korea University Transformation from WC to VC n Translation n View reference point (x 0, y 0, z 0) Jung Lee, airjung@korea. ac. kr 26 Computer Graphics Laboratory

Korea University Transformation from WC to VC n Rotation by uvn system n Calculate unit uvn vectors n n N: view-plane normal vector V: view-up vector U: perpendicular to both N and V Form the composite rotation matrix Jung Lee, airjung@korea. ac. kr 27 Computer Graphics Laboratory

Korea University Source Example float ele[16]; MATRIX t, r, wc 2 vc; t. Trans(-x 0, –y 0, -z 0); for(int i=0; i<15; i++) ele[i] = 0; ele[15] = 1. 0; for(i=0; i<3; i++) { ele[i] = u[i]; ele[4+i] = v[i]; } r. Createfrom. Elements(ele); ele[8+i] = n[i]; wc 2 vc = r. Multiply(t); Jung Lee, airjung@korea. ac. kr 28 Computer Graphics Laboratory