Koorde A Simple Degree Optimal DHT Frans Kaashoek

Koorde: A Simple Degree Optimal DHT Frans Kaashoek, David Karger MIT Brought to you by the IRIS project 1

DHT Routing n Distributed hash tables n n Implement hash table interface Map any ID to the machine responsible for that ID (in a consistent fashion) Standard primitive for P 2 P Machines not all aware of each other n n Each tracks small set of “neighbors” Route to responsible node via sequence of “hops” to neighbors 2

Performance Measures n Degree n n Hop count n n How many nodes can fail Maintenance overhead n n How long to reach any destination node Fault tolerance n n How many neighbors nodes have E. g. , making sure neighbors are up Load balance n How evenly keys distribute among nodes 3

Tradeoffs n With larger degree, hope to achieve n n n But higher degree implies n n n Smaller hop count Better fault tolerance More routing table state per node Higher maintenance overhead to keep routing tables up to date Load balance “orthogonal issue” 4

Current Systems n n Chord, Kademlia, Pastry, Tapestry O(log n) degree O(log n) hop count O(log n) ratio load balance n n Chord: O(1) load balance with O(log n) “virtual nodes” per real node Multiplies degree to O(log 2 n) 5

Outliers n CAN n n n Degree d O(dn 1/d) hops Viceroy n n n O(log n) hop count Constant average degree But some nodes have degree log n 6

Lower Bounds to Shoot For n Theorem: if max degree is d, then hop count is at least logd n n n Proof: < dh nodes at distance h Allows degree O(1) and O(log n) hops Or deg. O(log n) and O(log n / loglog n) hops Theorem: to tolerate half nodes failing, (e. g. net partition) need degree W(log n) n n Pf: if less, some node loses all neighbors Might as well take O(log n / loglog n) hops! 7

Koorde n n n New routing protocol Shares almost all aspects with Chord But, meets (to within constant factor) all lower bounds just mentioned: n n n Degree 2 and O(log n) hops Or degree log n and O(log n / loglog n) hops and fault tolerant Like Chord, O(log n) load balance n or constant with O(log n) times degree 8

Chord Review n Chord consists of n Consistent hashing to assign IDs to nodes n n ■ n Efficientroutingprotocoltotofindrightnode Koorde Fast join/leave protocol n n n Good load balance Few data items shifted Fault tolerance to half of nodes failing Efficient maintenance over time 9

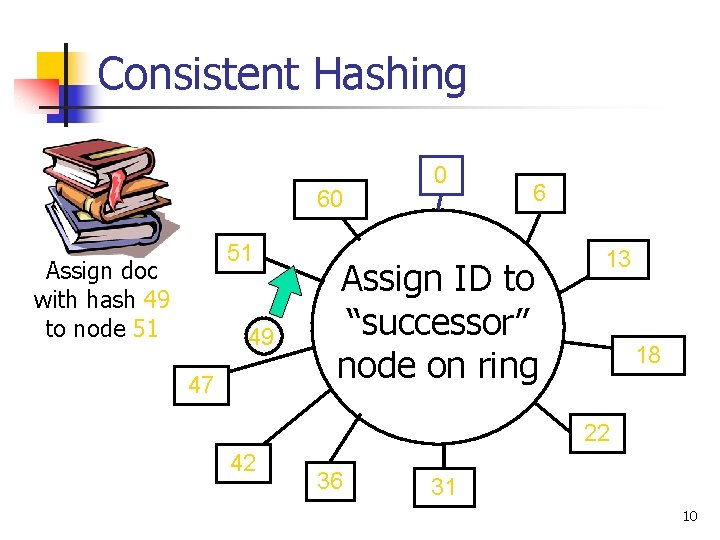
Consistent Hashing 60 51 Assign doc with hash 49 to node 51 49 47 0 6 Assign ID to “successor” node on ring 13 18 22 42 36 31 10

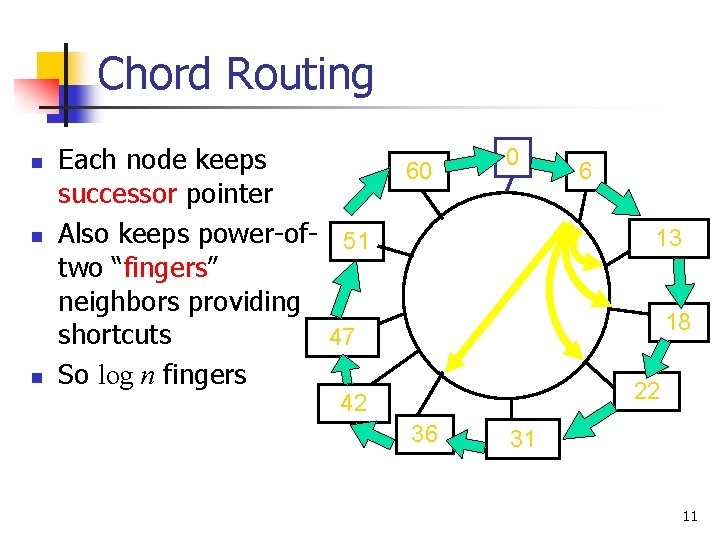
Chord Routing n n n Each node keeps successor pointer Also keeps power-of- 51 two “fingers” neighbors providing shortcuts 47 So log n fingers 60 0 6 13 18 22 42 36 31 11

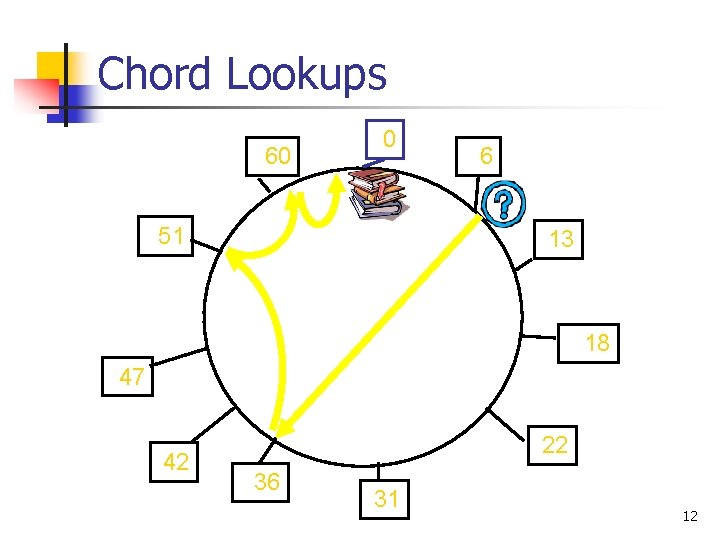
Chord Lookups 60 0 51 6 13 18 47 42 22 36 31 12

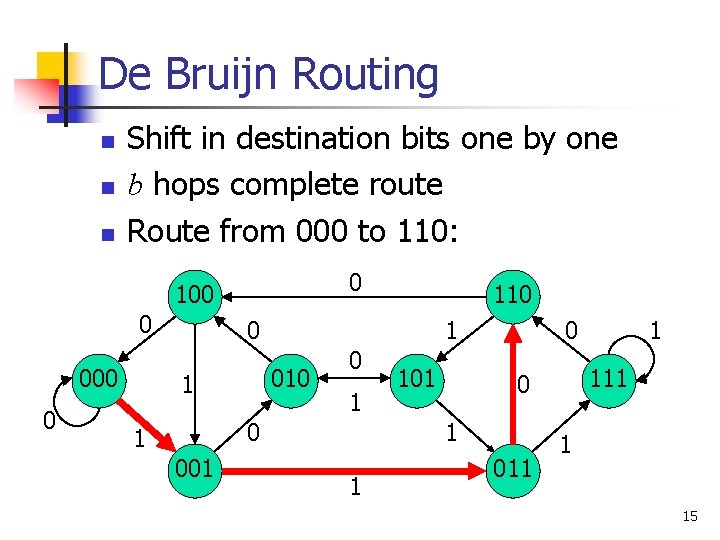
Koorde Idea n Chord acts like a hypercube n n Fingers flip one bit Degree log n (log n different flips) Diameter log n Koorde uses a de. Bruijn network n n n Fingers shift in one bit Degree 2 (2 possible bits to shift in) Diameter log n 13

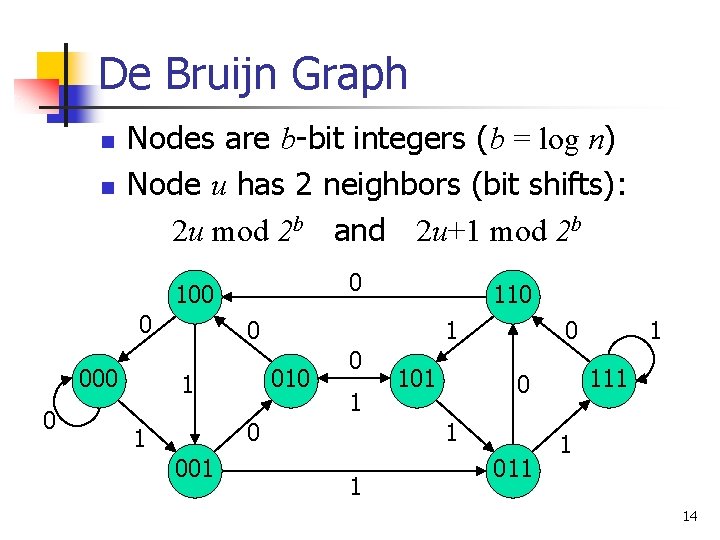
De Bruijn Graph n n Nodes are b-bit integers (b = log n) Node u has 2 neighbors (bit shifts): 2 u mod 2 b and 2 u+1 mod 2 b 0 100 0 000 0 110 0 1 010 1 0 1 001 101 0 1 111 0 1 011 1 1 14

De Bruijn Routing n n n Shift in destination bits one by one b hops complete route Route from 000 to 110: 0 100 0 000 0 110 0 1 010 1 0 1 001 101 0 1 111 0 1 011 1 1 15

Routing Code n Procedure u. LOOKUP(k, to. Shift) /* u is machine, k is target key to. Shift is target bits not yet shifted in */ if k = u then Return u /* as owner for k */ else /* do de Bruijn hop */ t = u ° top. Bit(to. Shift) Return t. lookup(k, toshift áá 1) n Initially call self. LOOKUP(k, k) 16

Summary n Each node has 2 outgoing neighbors n n Also two incoming Can show good routing load balance Need b = log n bits for n distinct nodes So log n hops to route 17

Problems to Solve n Want b-bit ring, b >> log n, to avoid colliding identifiers as nodes join n Implies use b >> log n hops Worse, most nodes not present to route! Solutions n n Imaginary routing: present nodes simulate routing actions of absent nodes Short cuts: use gaps to start route with most of destination bits already shifted in 18

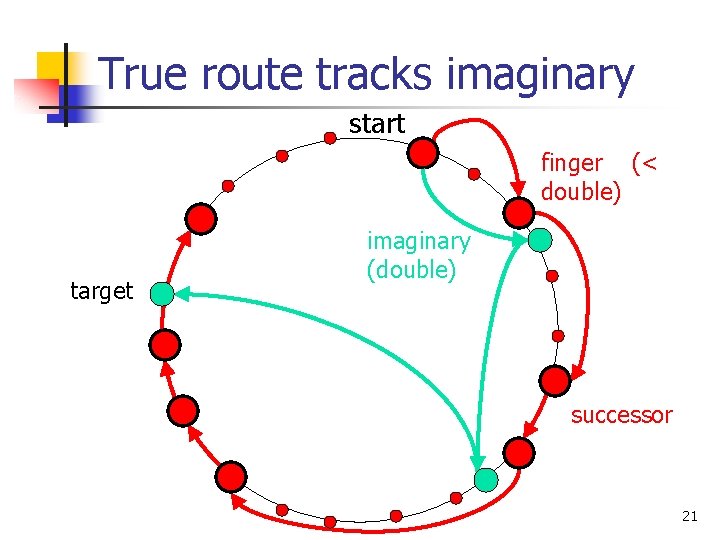
Imaginary routing n Node u holds two pointers n n Successor on ring One finger: predecessor of 2 u (mod 2 b) n n On sparse ring, is also predecessor of 2 u+1 So handles both de Bruijn edges Node u “owns” all imaginary nodes between self and (real) successor Simulates de Bruijn routing from those imaginary nodes to others by forwarding to the others’ real owners 19

Code n Procedure u. LOOKUP(k, to. Shift, i) if k Î (u, u. successor] then return u. successor /* as bucket for k */ else if i Î (u, u. successor] then /* i belongs to u; do de Bruijn hop */ return u. finger. LOOKUP(k, toshift áá 1, i ° top. Bit(to. Shift)) else /* i doesn’t belong to u; forward it */ return u. successor. LOOKUP(k, to. Shift, i) n Initially call self. LOOKUP(k, k, self) 20

True route tracks imaginary start finger (< double) target imaginary (double) successor 21

Correctness n Once b de Bruijn steps happen, done n n n Successor steps delay de Bruijn steps, but not forever n n At this point, i = k Will follow successors to bucket for k After finite number of successor steps, reach predecessor of i Conclude: all necessary de Bruijn steps happen in finite time. So correct. 22

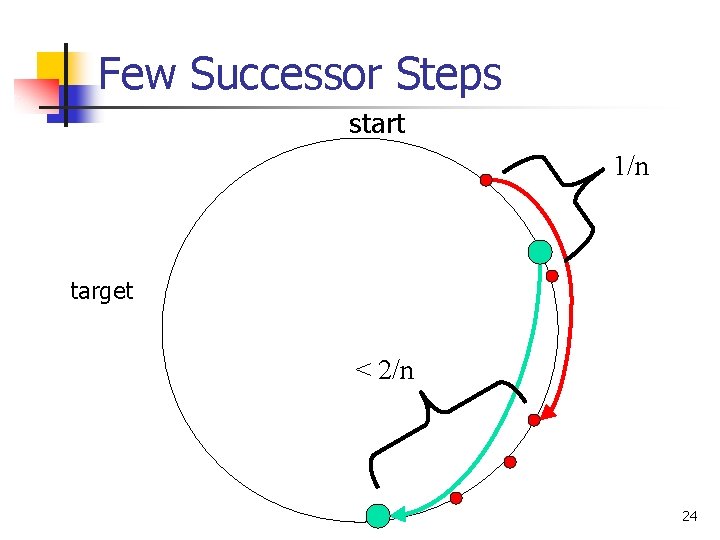
How long? n n Only b de Bruijn steps Just bound (expected) number of successor steps per de Bruijn step n n n Nodes randomly distributed on ring So node expects to own size 1/n interval So distance to imaginary node on de Bruijn step is 1/n De Bruijn step doubles everything, makes distance 2/n Expect 2 nodes in interval of that size 23

Few Successor Steps start 1/n target < 2/n 24

Summary n n n Each de Bruijn hop followed by 2 successor hops (in expectation) b de Bruijn hops Conclude 2 b successor hops so 3 b hops in total Expectation argument extends to “with high probability” argument (same bounds) Remaining problem: b>>log n, too big 25

Exploit Address Blocks n n n n Only n real nodes Each owns ~1/n “block” of keyspace Within that block, only top log n bits “significant”; low bits arbitrary So set low bits to high bits of target Then just have to shift out log n most significant bits So log n de Bruijn hops, So O(log n) hops in total 26

Example n n n Start at u = 001011011… Successor 001110101…. u “owns” imaginary 00101****** Target 1101011…. Set imaginary start 001011101011… Only need to shift out 00101 n 5 hops, independent of b 27

Summary n Koorde uses n n n 2 neighbors per node (one successor, one finger) And requires O(log n) routing hops with high probability 28

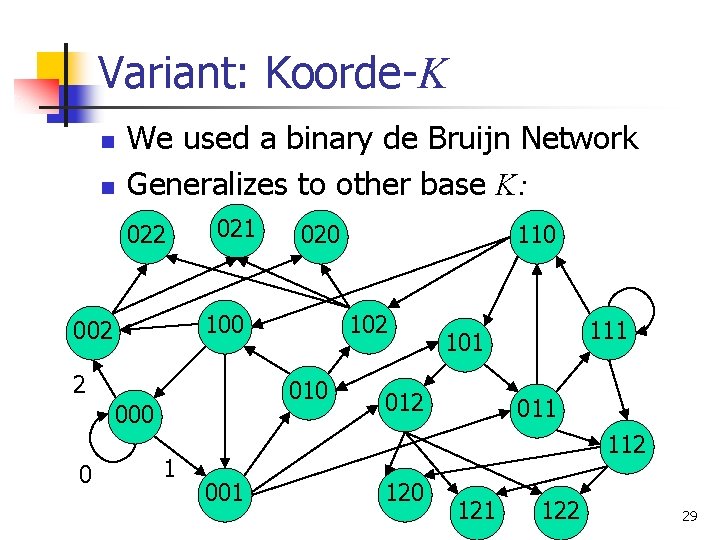
Variant: Koorde-K n n We used a binary de Bruijn Network Generalizes to other base K: 022 021 2 010 000 1 110 102 100 002 0 020 111 101 012 011 112 001 120 121 122 29

Analysis n To represent n distinct node ids need log. K n base-K digits n n Suggests log. K n hops to route Same problem as Koorde: b >> log. K n n Same solution: imaginary routing Node u points at predecessor(Ku) Same analysis: K de Bruijn hops interspersed with successor hops 30

Successor Hops n Now de Bruijn hop multiplies ids by K n n So expect K nodes between finger and next imaginary node Implies K successor hops per de Bruijn hop Gives K log. K n hops---no good To avoid successor hops, u fingers predecessor(Ku) and following K nodes n n Allows K successor hops by one finger Gives O(log. K n) hops as desired 31

Summary n n n Using K fingers per node, can achieve O(log. K n) = O(log n / log K) routing hops As discussed earlier, degree log n is necessary (and sufficient) for fault tolerance (and is degree of most previous systems) So, O(log n / log n ) hops 32

Summary: What do we Gain? n Lower degree for same number of hops n n n Storage isn’t really an issue But lower degree should translate into lower maintenance traffic Lower hop count for same degree n n n And tunable Other systems also have tunable hop count But at low hop counts (high degree) their extra log factor in degree does matter 33

What do we lose? n Chord is “self stabilizing” n n From successors, can build entire routing system quickly by “pointer jumping” to find fingers Koorde is not n n n Given only successor pointers, no clear fast way to find fingers Not a problem for joins, because joiner can use lookup to find its finger But could be a problem if massive changes 34

More Info http: //www. pdos. lcs. mit. edu/chord/ 35