Konsep Matriks Macammacam Matriks Kompetensi Dasar Mendeskripsikan macammaca

Konsep Matriks

Macam-macam Matriks Kompetensi Dasar : Mendeskripsikan macam-maca matriks Indikator : 1. Matriks ditentukan unsur dan notasinya 2. Matriks dibedakan menurut jenis dan relasinya Hal. : Matriks Adaptif

Macam – macam Matriks Pengertian Matriks v Matriks adalah susunan bilangan-bilangan yang terdiri atas baris dan kolom-kolom. v Masing-masing bilangan dalam matriks disebut entri atau elemen. Ordo (ukuran) matriks adalah jumlah baris kali jumlah kolom. Notasi: Matriks: A = [aij] Elemen: (A)ij = aij A= a 11 a 21 : ai 1 : am 1 a 12……. a 1 j ……a 1 n a 22 ……a 2 j……. a 2 n : : : ai 2 ……aij……. . ain : : : am 2……amj……. amn baris kolom Ordo A: m x n Hal. : Matriks Adaptif

Macam-macam Matriks 1. Matriks Baris Matriks baris adalah matriks yang hanya terdiri dari satu baris. 2 Hal. : 5 1 -8 -2 0 25 14 8 Matriks Adaptif

Macam-macam Matriks 2. Matriks Kolom adalah matriks yang hanya terdiri dari satu kolom 2 -7 9 2 1 Hal. : Matriks Adaptif

Macam – macam Matriks 3. Matriks Persegi Matriks persegi (bujur sangkar) adalah matriks yang jumlah baris dan jumlah kolom sama. 1 2 4 2 2 2 3 3 3 Trace(A) = 1 + 2 + 3 diagonal utama Trace dari matriks adalah jumlahan elemen-elemen diagonal utama Hal. : Matriks Adaptif

DETERMINAN DAN INVERS Contoh: Invers matriks 2 x 2 A= A-1 = Hal. : 3 2 4 1 = I Matriks Adaptif

Macam- macam Matriks 4. Matriks Nol Matriks nol adalah matriks yang semua elemennya nol 0 0 0 0 Matriks identitas adalah matriks persegi yang elemen diagonal I 3 I 4 utamanya 1 I 2 dan elemen lainnya 0 Hal. : 1 0 1 0 0 0 0 1 0 0 0 0 1 Matriks Adaptif

Macam-macam Matriks 5. Matriks ortogonal Matriks A orthogonal jika dan hanya jika AT = A – 1 A= B= 0 -1 1 0 AT= ½√ 2 -½√ 2 B T= 0 1 -1 0 = A-1 ½√ 2 -½√ 2 = B-1 (A A-1 -1)T = (A AT)-1 Jika A adalah matriks orthogonal, maka (A-1)T = (AT)-1 Hal. : Matriks Adaptif

Macam – macam Matriks A= 4 2 6 7 5 3 -9 7 AT = A’ = 4 5 2 3 6 -9 7 7 Definisi: Transpose mariks A adalah matriks AT kolom-kolomnya adalah baris-baris dari A, baris-barisnya adalah kolom-kolom dari A. [AT]ij = [A]ji nxm Jika A adalah matriks m x n, maka matriks transpose AT berukuran ………. . Hal. : Matriks Adaptif

Macam – macam Matriks Kesamaan dua matriks » Dua matriks sama jika ukuran sama dan setiap entri yang bersesuaian sama. A= C= E= G= Hal. : 1 2 4 2 1 3 1 2 2 2 1 3 1 2 4 2 2 2 B= D= F= 2 2 2 4 5 6 H= 5 9 0 7 1 2 4 2 1 3 2 1 2 2 1 3 x 2 4 2 2 ? 4 ? 9 ? 2 ? 5 ? 0 ? Matriks A=B C≠D E = F jika x = 1 2 ? 6 ? 7 ? G=H Adaptif

Macam-macam Matriks Simetri Matriks A disebut simetris jika dan hanya jika A = AT A= A = Hal. : 1 2 3 4 4 2 2 3 2 5 7 0 A’ = 3 7 8 2 4 0 2 9 4 2 2 3 A simetri = AT Matriks Adaptif

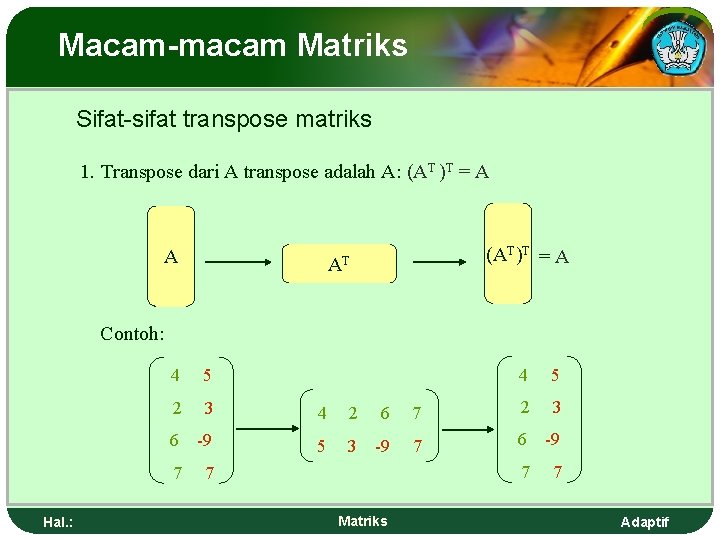
Macam-macam Matriks Sifat-sifat transpose matriks 1. Transpose dari A transpose adalah A: (AT )T = A A (AT)T = A AT Contoh: 4 5 2 3 4 2 6 6 -9 5 3 -9 7 Hal. : 4 5 7 2 3 7 6 -9 7 7 Matriks 7 Adaptif

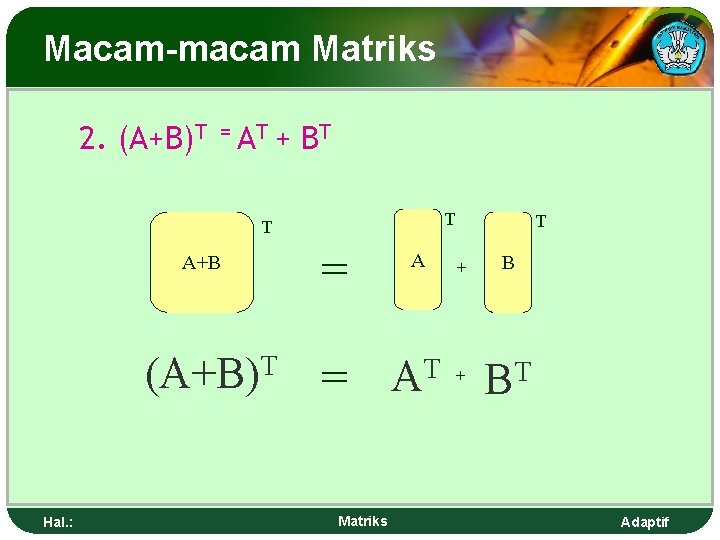
Macam-macam Matriks 2. (A+B)T = AT + BT T T A+B T (A+B) Hal. : = A T + B T + A = BT Matriks Adaptif

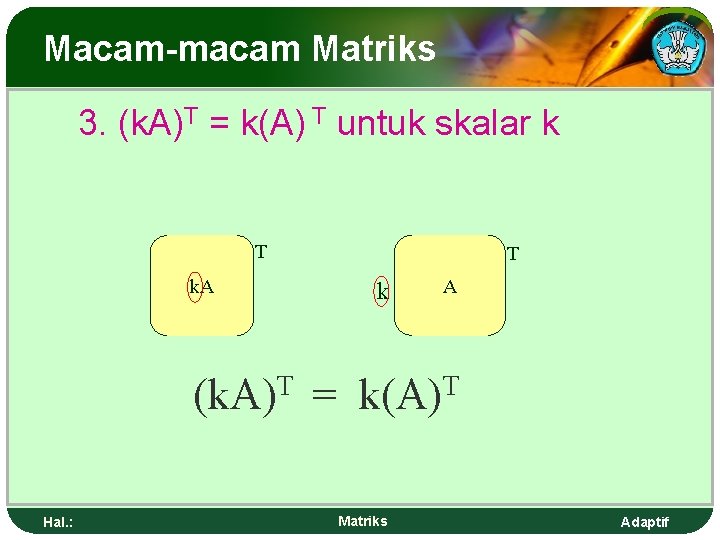
Macam-macam Matriks 3. (k. A)T = k(A) T untuk skalar k T T k. A T (k. A) Hal. : k = A T k(A) Matriks Adaptif

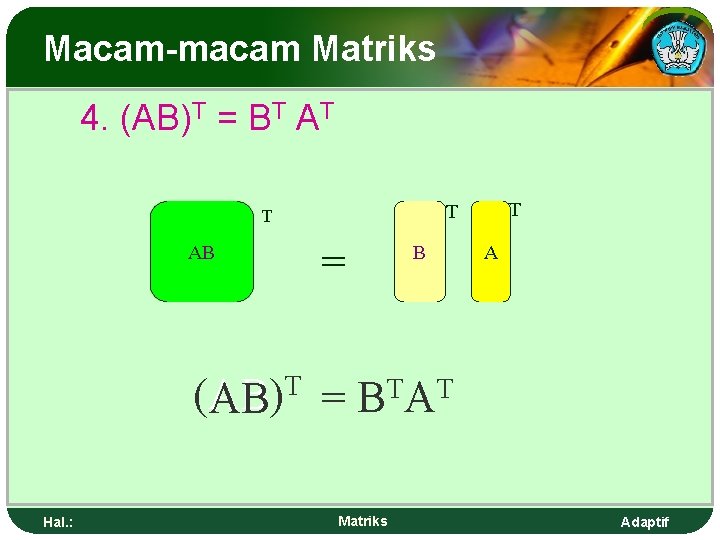
Macam-macam Matriks 4. (AB)T = BT AT AB = T (AB) = B T AT AB Hal. : T T T Matriks B A Adaptif

Macam-macam Matriks Soal : Isilah titik-titik di bawah ini 1. A simetri maka A + AT= ……. . 2. ((AT)T)T = ……. 3. (ABC)T = ……. 4. ((k+a)A)T = …. . . 5. (A + B + C)T = ………. Kunci: 1. 2 A 2. AT 3. CTBTAT 4. (k+a)AT 5. AT + BT + CT Hal. : Matriks Adaptif

OPERASI MATRIKS Kompetesi Dasar Menyelesaikan Operasi Matriks Indikator 1. 2. Hal. : Dua matriks atau lebih ditentukan hasil penjumlahan atau pengurangannya Dua matriks atau lebih ditentukan hasil kalinya Matriks Adaptif

OPERASI MATRIKS Penjumlahan dan pengurangan dua matriks Contoh : A= A+B= A-B= Hal. : 10 22 1 -1 B= 10+2 22+6 1+7 -1+5 10 -2 22 -6 1 -7 -1 -5 2 6 7 5 = 12 28 8 4 8 16 -6 -6 = Matriks Adaptif

OPERASI MATRIKS Apa syarat agar dua matriks dapat dijumlahkan? Jawab: Ordo dua matriks tersebut sama A = [aij] dan B = [bij] berukuran sama, A + B didefinisikan: (A + B)ij = (A)ij + (B)ij = aij + bij Hal. : Matriks Adaptif

OPERASI MATRIKS Jumlah dua matriks K= C= C+D K+L 1 3 5 4 -9 7 0 9 -13 5 6 1 7 2 3 = = 7 3 1 -2 4 -5 9 -4 3 L = D = ? ? ? ? 25 30 5 35 10 15 D+C L+K = = Apa kesimpulanmu? Apakah jumlahan matriks bersifat komutatif? Hal. : Matriks Adaptif

OPERASI MATRIKS v Soal: C= A = 3 -8 0 4 4 7 5 -1 8 0 0 0 3 7 2 D 2= 4 5 2 4 5 -1 8 0 0 0 B = 6 E = 4 Feedback: C +D = v v v Hal. : C + D =… C+E=… A+B=… Matriks 2 7 2 5 2 6 6 -1 2 9 9 8 -2 16 8 Adaptif

OPERASI MATRIKS Hasil kali skalar dengan matriks A= 5 6 1 7 2 3 5 A = 5 x 5 5 x 6 5 x 1 5 x 5 5 x 2 5 x 3 = 25 30 5 35 10 15 Apa hubungan H dengan A? H= 250 300 50 350 100 150 H = 50 A Diberikan matriks A = [aij] dan skalar c, perkalian skalar c. A mempunyai entri-entri sebagai berikut: (c. A)ij = c. (A)ij = caij Catatan: Pada himpunan Mmxn, perkalian matriks dengan skalar bersifat tertutup (menghasilkan matriks dengan ordo yang sama) Hal. : Matriks Adaptif

OPERASI MATRIKS v K 3 x 3 K= 4 K = 5 K = Hal. : 1 3 5 4 -9 7 0 9 -13 4 16 -36 12 28 0 20 36 -52 5 20 -45 15 35 0 25 45 -65 Matriks Adaptif

OPERASI MATRIKS v Diketahui bahwa c. A adalah matriks nol. Apa kesimpulan Anda tentang A dan c? Contoh: cc == 70 c. A = AA == 0*2 7*0 0*7 7*0 0*2 0*5 7*0 0*2 7*0 0*6 = 20 70 20 50 20 60 0 0 0 kesimpulan Kasus 1: c = 0 dan A matriks sembarang. Kasus 2: A matriks nol dan c bisa berapa saja. Hal. : Matriks Adaptif

OPERASI MATRIKS Perkalian matriks dengan matriks v Definisi: § Jika A = [aij] berukuran m x r , dan B = [bij] berukuran r x n, maka matriks hasil kalir A dan B, yaitu C = AB mempunyai elemen yang didefinisikan sebagai berikut: (C)ij = (AB)ij = ∑ aikbkj = ai 1 b 1 j +ai 2 b 2 j+………airbrj k=1 • Syarat: A= Hal. : A mxr B rxn 2 3 4 5 8 -7 9 -4 1 -5 7 -8 AB mxn B= Matriks 1 2 7 -6 4 -9 Tentukan AB dan BA Adaptif

OPERASI MATRIKS Perkalian matriks dengan matriks Contoh : 2 A= 3 4 1 5 8 -7 9 -4 1 -5 7 -8 B= 2 7 -6 4 -9 11 3 = AB = 2. 1 +3. 7+4. 4+5. 11 -35 -49 -35 -94 -55 94 -35 = -49 -35 -94 -55 BA tidak didefinisikan Hal. : Matriks Adaptif

OPERASI MATRIKS 1. Diberikan A dan B, AB dan BA terdefinisi. Apa kesimpulanmu? A B B A mxn nxk mxn m=k ABmxm AB dan BA matriks persegi ABnxn 2. AB = O matriks nol, apakah salah satu dari A atau B pasti matriks nol? A= 2 2 3 3 B= 3 -3 -2 2 AB = 0 0 AB matriks nol, belum tentu A atau B matriks nol Hal. : Matriks Adaptif

OPERASI MATRIKS Contoh 1: Tentukan hasil kalinya jika terdefinisi. A= C= • • • Hal. : A B = ? ? AC = ? ? BD = ? ? CD = ? ? DB = ? ? 2 4 2 3 7 3 4 9 5 7 -11 4 3 5 -6 5 0 6 B= D= Matriks 1 -9 8 5 2 0 0 6 1 8 9 5 6 2 5 6 -9 0 0 -4 7 8 9 Adaptif

OPERASI MATRIKS Contoh 2: A= 2 1 3 2 A 2 = 2 1 3 2 A 3 = A x A 2 = 2 1 3 2 A 0 = I An = A A A …A n faktor An+m = An Am Hal. : Matriks Adaptif

DAN DETERMINAN INVERS Kompetensi Dasar: Menentukan determinan dan invers Indikator : 1. Matriks ditentukan determinannya 2. Matriks ditentukan inversnya Hal. : Matriks Adaptif

DETERMINAN DAN INVERS Determinan Matriks ordo 2 x 2 Nilai determinan suatu matriks ordo 2 x 2 adalah hasil kali elemen diagonal utama dikurangi hasil kali elemen pada diagonal kedua. Misalkan diketahui matriks A berordo 2 x 2, A = Determinan A adalah det A = Hal. : = ad - bc Matriks Adaptif

DETERMINAN DAN INVERS B adalah invers dari matriks A, jika AB = BA = I matriks identitas, ditulis B = A-1 A Jika A = Hal. : A-1 = A-1 A = I , maka Matriks Adaptif

DETERMINAN DAN INVERS Contoh 1 : Tentukan invers dari matriks Jawab : det B = (-5). (-4) – (-2). (-10) = 20 – 20 = 0 , sehingga matriks B tidak memiliki invers Hal. : Matriks Adaptif

DETERMINAN DAN INVERS Contoh : 1. Kapan matriks TIDAK mempunyai invers? ad-bc = 0 2. Tentukan invers matriks berikut ini a. b. c. d. Hal. : 5 1 1 2 0 1 0 2 0 0 4 1 1 0 0 1 a. 2/3 -1/5 5/3 b. tidak mempunyai invers c. tidak mempunyai invers d. Matriks 1 0 0 1 Adaptif

DETERMINAN DAN INVERS Contoh 2 : Diketahui matriks Tunjukkan bahwa A. A-1 = A-1. A = I dan B. B-1 = B-1. B = I 4 2 ½ -½ 2 2 -½ 1 A-1 A = 2 1 ½ -½ 1 2 2 1 -½ -½ 1 3 3 1 0 3 -2 Hal. : 4 2 -½ 2 2 1 A-1 4 B ½ -½ B-1 = = A 2 1 ½ -½ 1 2 2 1 -½ -½ 1 3 3 1 0 3 -2 Matriks 0 0 1 I 4 B-1 1 B = 1 0 0 0 1 I Adaptif

DETERMINAN DAN INVERS Matriks ordo 3 x 3 Determinan Matriks Ordo 3 x 3 Dengan aturan Sarrus, determinan A adalah sebagai berikut. _ _ Hal. : _ + + + Matriks Adaptif

DETERMINAN DAN INVERS Sistem Persamaan Linear Dua Variabel dengan Menggunakan Matriks Misal SPL Persamaan tersebut dapat di ubah menjadi bentuk matriks berikut Hal. : Matriks Adaptif

DETERMINAN DAN INVERS Misalkan Hal. : maka dapat ditulis Matriks Adaptif

DETERMINAN DAN INVERS Contoh : Tentukan nilai x dan y yang memenuhi sistem persamaan linear Jawab : Sistem persamaan Jika dibuat dalam bentuk matriks menjadi Hal. : Matriks Adaptif

DETERMINAN DAN INVERS Perkalian matriks berbentuk AP = B dengan Jadi nilai x = 5 dan y = 2 Hal. : Matriks Adaptif

DETERMINAN DAN INVERS Penyelesaian sistem persamaan linear dua variabel dengan menggunakan determinan atau aturan Cramer. Misal SPL Maka dengan aturan Cramer, diperoleh dan Hal. : Matriks Adaptif

DETERMINAN DAN INVERS Contoh : Gunakan aturan Cramer untuk menentukan himpunan penyelesaian sistem persamaan linear Jawab : Dengan aturan Cramer diperoleh Jadi, himpunan penyelesaiannya adalah {(1, 2)}. Hal. : Matriks Adaptif

DETERMINAN DAN INVERS v Menyelesaikan Sistem Persamaan Linear Tiga Variabel dengan menggunakan Matriks v SPL dalam bentuk: a 11 x 1 + a 12 x 2 + a 13 x 3 +…. . a 1 nxn = b 1 a 21 x 1 + a 22 x 2 + a 23 x 3 +……. a 2 nxn = b 2 am 1 x 1 + am 2 x 2 + am 3 x 3 + ……amnxn = bm v Dapat disajikan dalam bentuk persamaan matriks: = x 1 b 1 a 12……. . . a 1 n x 2 b 2 a 21 a 22 ……. . a 2 n : : : xn bn am 1 am 2…… amn x A: matriks koefisien b Ax = b Hal. : Matriks Adaptif

DETERMINAN DAN INVERS Contoh : SPL x 1 + 2 x 2 + x 3 = 6 -x 2 + x 3 = 1 4 x 1 + 2 x 2 + x 3 = 4 Dapat disajikan dalam bentuk matriks sebagai berikut 1. x 1 +2. x 2 + 1. x 3 0. x 1 + -1. x 2 + 1. x 3 4. x 1 +2. x 2 + 1. x 3 Hal. : = 6 1 2 1 x 1 1 0 -1 1 x 2 4 4 2 1 x 3 Matriks 6 = 1 4 Adaptif

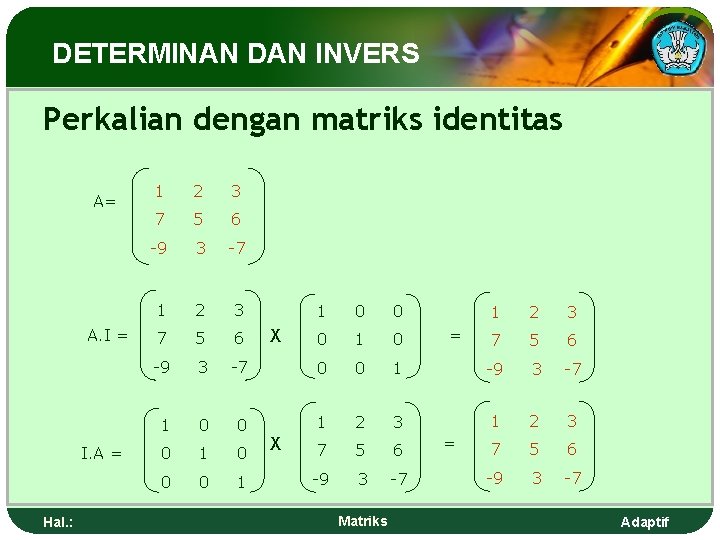
DETERMINAN DAN INVERS Perkalian dengan matriks identitas A= A. I = I. A = Hal. : 1 2 3 7 5 6 -9 3 -7 1 2 3 7 5 6 -9 3 1 1 0 0 0 1 0 -7 0 0 1 0 0 0 1 X X 1 2 3 7 5 6 1 -9 3 -7 2 3 1 2 3 7 5 6 -9 3 -7 Matriks = = Adaptif

DETERMINAN DAN INVERS AB = A dan BA = A, apa kesimpulanmu? 1 3 5 4 -9 7 0 9 -13 1 0 0 1 = 1 0 0 1 1 3 5 4 -9 7 0 9 -13 = A I = I A 1 3 5 4 -9 7 0 9 -13 = A AB = A dan BA = A, maka B = I (I matriks identitas) Hal. : Matriks Adaptif

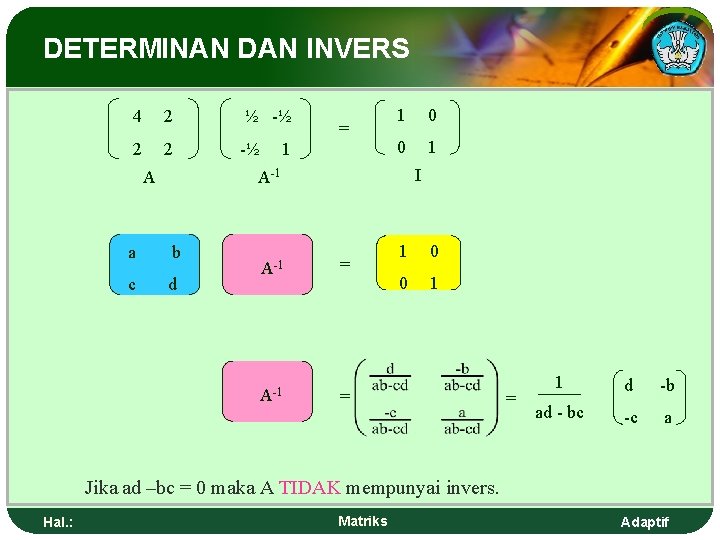
DETERMINAN DAN INVERS 4 2 ½ -½ 2 2 -½ = 1 1 0 0 1 I A-1 A a b c d A-1 = 1 0 0 1 = = 1 d -b ad - bc -c a Jika ad –bc = 0 maka A TIDAK mempunyai invers. Hal. : Matriks Adaptif

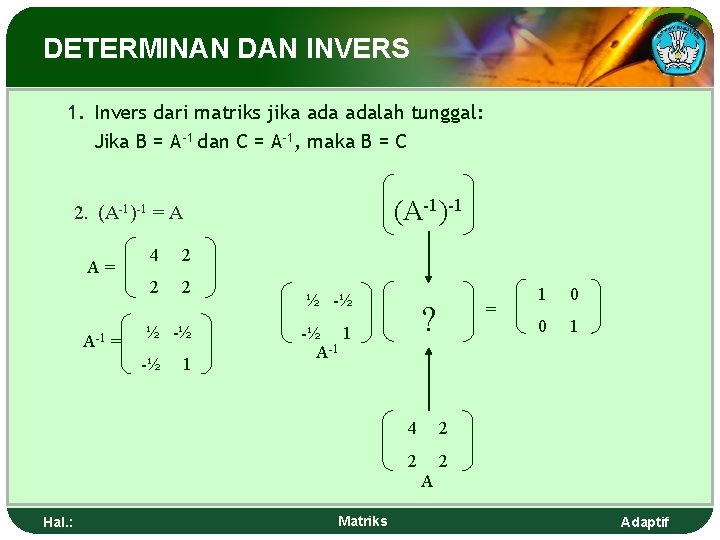
DETERMINAN DAN INVERS 1. Invers dari matriks jika adalah tunggal: Jika B = A-1 dan C = A-1, maka B = C (A-1)-1 2. (A-1)-1 = A A= A-1 = 4 2 2 2 ½ -½ -½ 1 ½ -½ ? -½ 1 A-1 = 4 2 2 2 1 0 0 1 A Hal. : Matriks Adaptif

DETERMINAN DAN INVERS 3. Jika A mempunyai invers maka An mempunyai invers dan (An)-1 = (A-1)n, n = 0, 1, 2, 3, … A= A 3 = (A 3)-1 = (A-1)3 = Hal. : 2 2 2 4 2 4 2 2 2 2 A-1 = -½ 0. 625 -1 sama ½ -½ 4 1 = 104 64 64 40 -1 1. 625 ½ -½ -½ 1 1 Matriks 1 = 0. 625 -1 -1 1. 625 Adaptif

DETERMINAN DAN INVERS 4. (AB)-1 = B-1 A= 4 2 2 2 (AB)-1 = B-1 A-1 = A-1 B-1 = Hal. : B= 16 24 10 14 3 5 2 2 -1 B-1 = 5/4 ½ -¾ -0. 875 1. 5 0. 625 -1 = ½ 5/4 ½ -½ ½ -¾ -½ 1 ½ -½ ½ 5/4 -½ ½ -¾ 1 ½ Matriks = = -0. 875 1. 5 0. 625 -1 -0. 5 1 0. 75 -1. 375 Adaptif