Kondo effect in charmbottom nuclei ar Xiv 1602

Kondo effect in charm/bottom nuclei ar. Xiv: 1602. 00227 [hep-ph] Shigehiro Yasui Tokyo Institute of Technology International workshop on J-PARC hadron physics in 2016@KEK, Tokai, 2 -4 Mar. 2016

1. Multi-flavor nucleus Nucleus + Strangeness 1. Hadron-nucleon interaction 2. Hadron in medium 3. Nuclear structure Impurity physics

1. Multi-flavor nucleus S. H. Lee’s talk D. Suenaga’s talk Nucleus + Charm Mass hierarchy (m >>Λ c ~1. 2 Ge. V QCD) ~0. 2 Ge. V 1. Hadron-nucleon interaction ? ? 3. Nuclear structure ? Impurity physics 2. Hadron in medium

1. Multi-flavor nucleus Charm nucleus mass spectroscopy D, D* - Binding energy - Dispersion relation - Spectral function - Reaction - Restoration of χSB - Nuclear structure - etc. q c Nucleus Kondo effect : quantum impurity physics

Contents 1. Multi-flavor nucleus 2. Kondo effect 2. 1 What’s Kondo effect? 2. 2 Kondo effect in atomic nuclei (mean-field + RPA) 3. Conclusion Mean-field approach to Kondo effect bulk systems F. Takano, T. Ogawa, Prog. Theor. Phys. 35, 343 (1966) A. Yoshimori, A. Sakurai, Suppl. Prog. Theor. Phys. 46, 162 (1970) M. Eto, Y. V. Narazov, Phys. Rev. B 64, 085322 (2001) finite systems This work

2. Kondo effect JUN KONDO (1930 -)

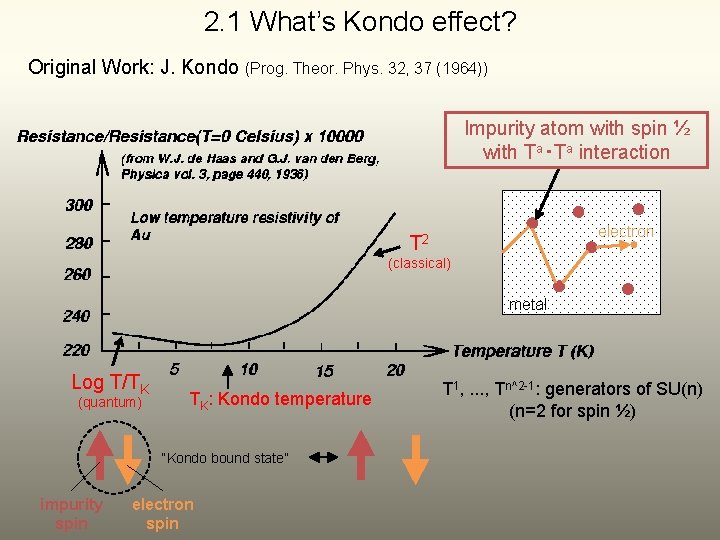
2. 1 What’s Kondo effect? Original Work: J. Kondo (Prog. Theor. Phys. 32, 37 (1964)) Impurity atom with spin ½ with Ta・Ta interaction electron T 2 (classical) metal Log T/TK (quantum) TK: Kondo temperature “Kondo bound state” impurity spin electron spin T 1, . . . , Tn^2 -1: generators of SU(n) (n=2 for spin ½)

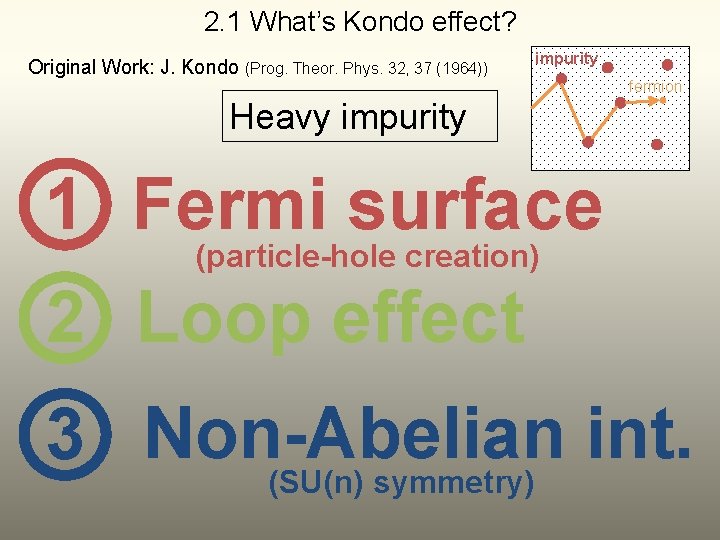
2. 1 What’s Kondo effect? Original Work: J. Kondo (Prog. Theor. Phys. 32, 37 (1964)) impurity fermion Heavy impurity 1 Fermi surface (particle-hole creation) 2 Loop effect int. 3 Non-Abelian (SU(n) symmetry)

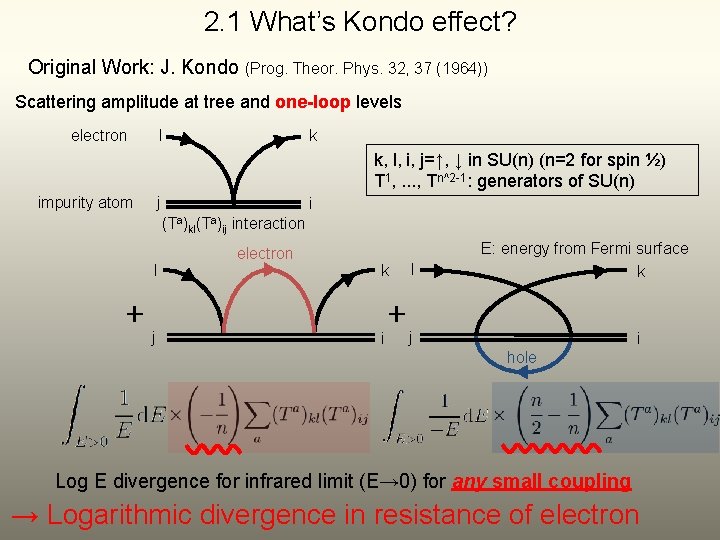
2. 1 What’s Kondo effect? Original Work: J. Kondo (Prog. Theor. Phys. 32, 37 (1964)) Scattering amplitude at tree and one-loop levels l electron k k, l, i, j=↑, ↓ in SU(n) (n=2 for spin ½) T 1, . . . , Tn^2 -1: generators of SU(n) impurity atom j i (Ta) l +j kl (Ta) ij interaction electron k l E: energy from Fermi surface k + j i i hole Log E divergence for infrared limit (E→ 0) for any small coupling → Logarithmic divergence in resistance of electron

2. 1 What’s Kondo effect? Application to nuclear/quark matter NJL-type: S. Y. , K. Sudoh, Phys. Rev. C 88, 015201 (2013) QCD: K. Hattori, K. Itakura, S. Ozaki, S. Y. , Phys. Rev. D 92, 065003 (2015) nucleon D, B meson (τa)kl(τa)ij interaction “Isospin Kondo effect” ① nuclear matter ② nucleon-hole loop ③ isospin SU(2) symmetry u, d, s quark c, b quark (λa)kl(λa)ij interaction “Color (QCD) Kondo effect” ① quark matter ② quark-hole loop ③ color SU(3) symmetry Cf. “Magnetic catalysis QCD Kondo effect” S. Ozaki, K. Itakura, Y. Kuramoto, ar. Xiv: 1509: 06966 [hep-ph]

2. 1 What’s Kondo effect? Application to nuclear/quark matter NJL-type: S. Y. , K. Sudoh, Phys. Rev. C 88, 015201 (2013) QCD: K. Hattori, K. Itakura, S. Ozaki, S. Y. , Phys. Rev. D 92, 065003 (2015) nucleon D, B meson (τa)kl(τa)ij interaction “Isospin Kondo effect” ① nuclear matter ② nucleon-hole loop ③ isospin SU(2) symmetry What’s about in atomic nuclei? (finite size nuclear systems) u, d, s quark c, b quark (λa)kl(λa)ij interaction “Color (QCD) Kondo effect” ① quark matter ② quark-hole loop ③ color SU(3) symmetry Cf. “Magnetic catalysis QCD Kondo effect” S. Ozaki, K. Itakura, Y. Kuramoto, ar. Xiv: 1509: 06966 [hep-ph]

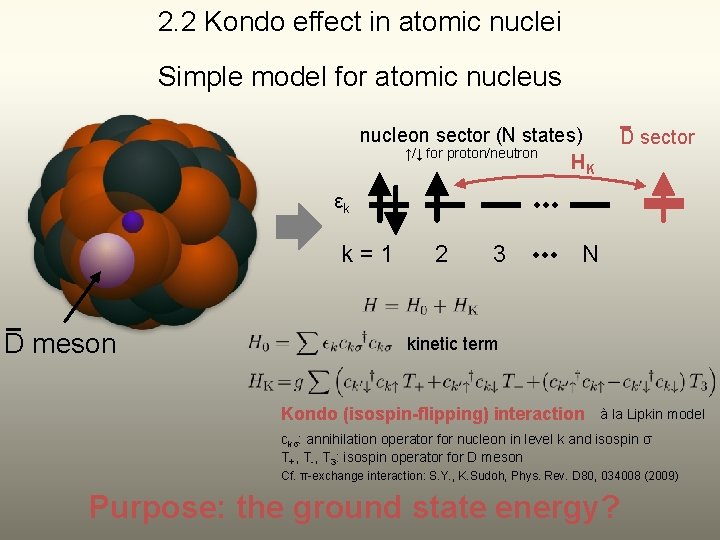
2. 2 Kondo effect in atomic nuclei Simple model for atomic nucleus nucleon sector (N states) ↑/↓ for proton/neutron HK D sector εk k=1 D meson 2 3 N kinetic term Kondo (isospin-flipping) interaction à la Lipkin model ckσ: annihilation operator for nucleon in level k and isospin σ T+, T-, T 3: isospin operator for D meson Cf. π-exchange interaction: S. Y. , K. Sudoh, Phys. Rev. D 80, 034008 (2009) Purpose: the ground state energy?

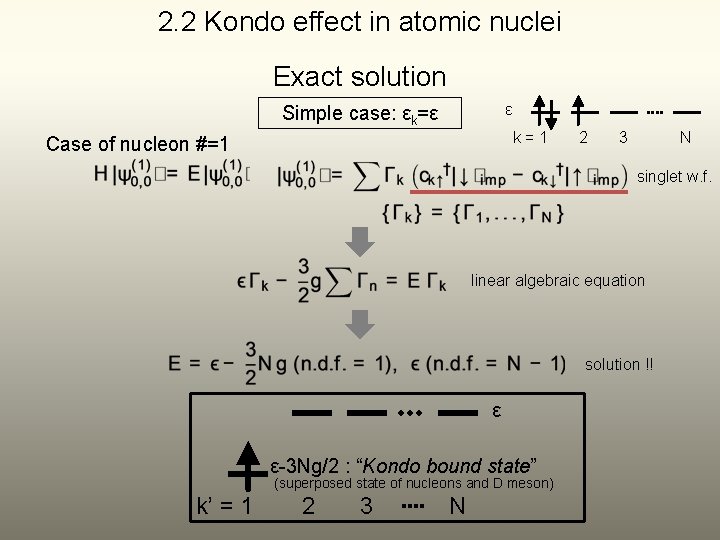
2. 2 Kondo effect in atomic nuclei Exact solution ε Simple case: εk=ε k=1 Case of nucleon #=1 2 3 N singlet w. f. linear algebraic equation solution !! ε ε-3 Ng/2 : “Kondo bound state” (superposed state of nucleons and D meson) k’ = 1 2 3 N

? k 2. 2 Kondo effect in atomic nuclei What’s about more general cases? r o Mean-field (+RPA) approach w t Step 1. Introduce auxiliary fermion fields fσ (SU(2)) e o i s fermion # 0, 2 fermion # 1 physical space auxiliary fermion # constraint Step 2. Introduce Lagrange multiplier λ w o H d Step 3. Apply mean-field (Δ) approx. Step 4. Variation by λ and Δ “gap” color singlet

2. 2 Kondo effect in atomic nuclei What’s about more general cases? Mean-field (+RPA) approach Step 1. Introduce auxiliary fermion fields fσ (SU(2)) fermion # 0, 2 fermion # 1 physical space auxiliary fermion # constraint Step 2. Introduce Lagrange multiplier λ Step 3. Apply mean-field (Δ) approx. Step 4. Variation by λ and Δ “gap” color singlet

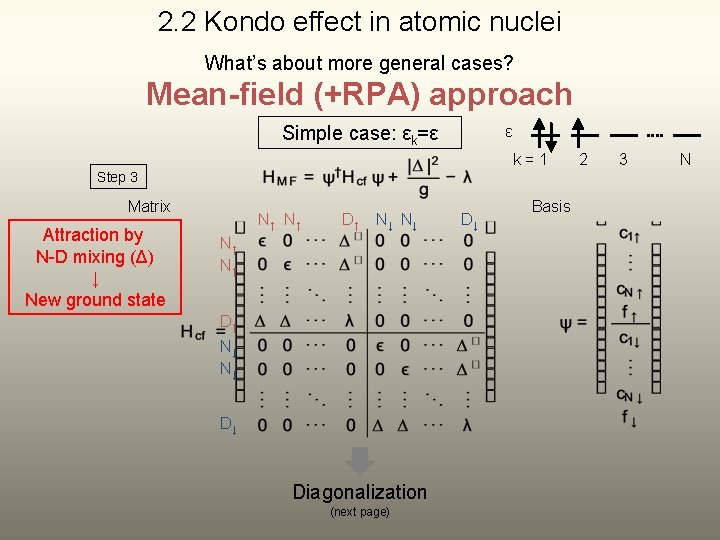
2. 2 Kondo effect in atomic nuclei What’s about more general cases? Mean-field (+RPA) approach Simple case: εk=ε ε k=1 Step 3 Matrix Attraction by N-D mixing (Δ) ↓ New ground state N↑ N↑ D↑ N↓ N↓ D↓ Diagonalization (next page) D↓ Basis 2 3 N

2. 2 Kondo effect in atomic nuclei What’s about more general cases? Mean-field (+RPA) approach Simple case: εk=ε ε k=1 2 3 N Step 3 Diagonalized matrix New basis lowest energy (↑) lowest energy (↓) Linear combination of (coherent) nucleon and D meson

2. 2 Kondo effect in atomic nuclei What’s about more general cases? Mean-field (+RPA) approach Simple case: εk=ε ε k=1 2 3 N Step 3 Diagonalized matrix lowest energy (↓) lowest energy (↑) Step 4 Variation by “Kondo bound state” Binding energy (MF): Ng different form exact solution 3 Ng/2?

2. 2 Kondo effect in atomic nuclei What’s about more general cases? Mean-field (+RPA) approach Simple case: εk=ε ε ① Mean-value of auxiliary fermion number is one. k=1 2 3 N ② Fluctuation effect random-phase ( approximation; RPA) zero-point energy in H. O. potential Binding energy (MF+RPA): 1. 378 Ng close to exact solution 3 Ng/2=1. 5 Ng!!

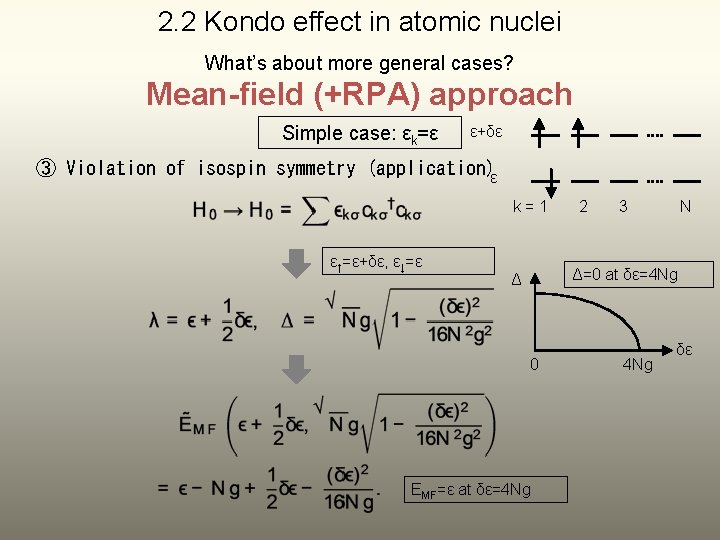
2. 2 Kondo effect in atomic nuclei What’s about more general cases? Mean-field (+RPA) approach Simple case: εk=ε ε+δε ③ Violation of isospin symmetry (application)ε k=1 ε↑=ε+δε, ε↓=ε 2 3 N Δ=0 at δε=4 Ng Δ 0 EMF=ε at δε=4 Ng δε

3. Conclusion 1. We study the ground state of charm nucleus (D meson) with isospin Kondo effect. Isospin-dependent interaction 2. We apply the mean-field + RPA approach x to. Nuclear withmodel D meson the ground system state in a simple in success. This method can be applied to realistic nuclear = 3. “Kondo bound state” structure with charm/bottom hadron. Future works: 1. Application to realistic D meson-nucleon interaction. 2. Effect by nuclear shell effects/collective modes. 3. Observables for experiments. 4. etc.

References HQS doublet/singlet in exotic hadrons and nuclei S. Y. , K. Sudoh, Y. Yamaguchi, S. Ohkoda, A. Hosaka, T. Hyodo, Phys. Lett. B 727, 185 (2013) Y. Yamaguchi, S. Ohkoda, T. Hyodo, A. Hosaka, S. Y. , Phys. Rev. D 91, 034034 (2015) D(*)N, D(*)NN hadronic molecules S. Y. , K. Sudoh, Phys. Rev. D 80, 034008 (2009) Y. Yamaguchi, S. Ohkoda, S. Y. , A. Hosaka, Phys. Rev. D 84, 014032 (2011) Y. Yamaguchi, S. Ohkoda, S. Y. , A. Hosaka, Phys. Rev. D 85, 054003 (2013) Y. Yamaguchi, S. Y. , A. Hosaka, Nucl. Phys. A 927, 110 (2014) D(*) in nuclear matter and Kondo effects S. Y. , K. Sudoh, Phys. Rev. C 87, 015202 (2013) S. Y. , K. Sudoh, Phys. Rev. C 88, 015201 (2013) NLO in 1/m. Q expansion for D(*) in nuclear matter S. Y. , K. Sudoh, Phys. Rev. C 89, 015201 (2014) D(*)N hadronic molecules Y. Yamaguchi, S. Ohkoda, S. Y. , A. Hosaka, Phys. Rev. D 87, 074019 (2013)

1. Multi-flavor nucleus D (B) meson in nuclear matter Quark-meson coupling model, QCD sum rules, hadronic interactions (mean-field approach, channel coupling, pion interaction), . . . Binding energy [Me. V] Quark-meson coupling model QCD rum rule Mean field Hadron dynamics WT-type coupling ~ a few ten Me. V -50 Me. V [27] +30 Me. V [28] -66 Me. V [29] (Repulsive? Attractive? ) [6] K. Tsushima, D. -H. Lu, A. W. Thomas, K. Saito and R. H. Landau, Phys. Rev. C 59, 2824 (1999). [7] A. Sibirtsev, K. Tsushima and A. W. Thomas, Eur. Phys. J. A 6, 351 (1999). [15] T. Hilger, R. Thomas and B. Kampfer, Phys. Rev. C 79, 025202 (2009). [16] T. Hilger, R. Schulze and B. Kampfer, J. Phys. G G 37, 094054 (2010). [17] Z. -G. Wang and T. Huang, Phys. Rev. C 84, 048201 (2011). [18] A. Mishra, E. L. Bratkovskaya, J. Schaffner-Bielich, S. Schramm and H. Stoecker, Phys. Rev. C 69, 015202 (2004). [19] M. F. M. Lutz and C. L. Korpa, Phys. Lett. B 633, 43 (2006). [20] L. Tolos, A. Ramos and T. Mizutani, Phys. Rev. C 77, 015207 (2008). [21] A. Mishra and A. Mazumdar, Phys. Rev. C 79, 024908 (2009). [22] A. Kumar and A. Mishra, Phys. Rev. C 81, 065204 (2010). [23] C. E. Jimenez-Tejero, A. Ramos, L. Tolos and I. Vidana, Phys. Rev. C 84, 015208 (2011). [24] A. Kumar and A. Mishra, Eur. Phys. J. A 47, 164 (2011). [25] C. Garcia-Recio, J. Nieves, L. L. Salcedo and L. Tolos, Phys. Rev. C 85, 025203 (2012). [26] S. Yasui, K. Sudoh, Phys. Rev. C 87, 015202 (2013). [27] A. Hayashigaki, Phys. Lett. B 487, 96 (2000) [28] K. Suzuki, P. Gubler, M. Oka, Pos Hadron 2013, 179 (2014). [29] K. Azzi, N. Er, H. Sundu, Eur. Phys. J. C 74, 3021 (2014). π exchange [26]