Kompresja danych Instytut Informatyki UWr Studia dzienne Wykad

Kompresja danych Instytut Informatyki UWr Studia dzienne Wykład nr 2: rozszerzone i dynamiczne Huffmana

Kod Huffmana - niemiłe przypadki. . . Niech alfabet składa się z 2 liter: P(a)=1/16 P(b)=15/16 Mamy H(1/16, 15/16) = -1/16*log(1/16)-15/16*log(15/16) 0. 34 Natomiast algorytm Huffmana daje kod K: K(a)=0 K(b)=1 Czyli S(K) = 1/16*1+15/16*1 = 1. . . żadnej kompresji, prawie 3 razy gorzej od entropii. . .

Kod Huffmana - rozszerzamy. . . Dla rozkładu prawdopodobieńtw jak poprzednio: P(A)=1/16 P(B)=15/16 Wprowadźmy rozszerzony alfabet {AA, AB, BA} Para P(para) Kod Huffm AA 1 / 256 100 AB 15 / 256 101 BB 225 / 256 0 BA 15 / 256 11 średnia długość powyższego kodu Huffmana: S(H) = 1/256 * 3 + 15/256 * 3 +15/256 * 2 + 225/256*1 1. 18 a entropia: H(1/256, 15/256, 225/256) 0. 68 Czyli już „tylko” niecałe 2 razy gorzej od entropii.

Uogólnijmy rozszerzanie. . . Uogólniamy (dla ciągów niezależnych): n Dany rozkład prawdopodobieństw P = { p 1, , pn } odpowiadający symbolom a 1, , an n k-tym rozszerzeniem Pk rozkładu P nazywamy rozkład odpowiadający wszystkim k-elementowym ciągom symboli ze zbioru { a 1, , an } n prawdopodobieństwo ciągu ai 1 aik w rozkładzie Pk to pi 1*pi 2* *pik Jak zmieni się entropia? n n rozkład prawdopodobieństwa oryginalnych symboli nie zmienił się! A zatem „zawartość informacyjna” danych również powinna ulec zmianie!!!

Entropia dla rozszerzonego alfabetu Twierdzenie Niech Pk będzie rozkładem prawdopodobieństw k-tego rozszerzenia alfabetu z rozkładem P. Wówczas: H(Pk) = k H(P) Dowód: k = 1: oczywiste Krok indukcyjny: Załóżmy, że H(Pk-1) = (k-1) H(P). Wówczas:

Dowód c. d.

Rozszerzony alfabet c. d. Skoro H(Pk) = k H(P) to znaczy, że zgodnie z intuicją n liczba „bitów informacji” przypadających na jeden symbol rozszerzonego alfabetu jest k-krotnie większa od liczby bitów „informacji” na symbol oryginalnego alfabetu n ale jeden symbol w Pk odpowiada k symbolom w P n czyli liczba bitów na „oryginalny” symbol nie zmienia się. A jak z jakością kodów Huffmana dla rozszerzonego alfabetu?

Jakość Huffmana dla rozszerzonego. . . Wniosek Średnia długość kodu Huffmana dla rozszerzonego alfabetu z rozkładem Pk odpowiadająca przypadająca na jeden symbol alfabetu oryginalnego wynosi co najwyżej H(P)+1/k. Dowód: Optymalność kodu Huffmana gwarantuje, że S( Huffmank ) H(Pk) + 1 gdzie Huffmank to kod Huffmana dla Pk. A zatem na jeden symbol alfabetu oryginalnego przypada co najwyżej: S( Huffmank ) / k (H(Pk) + 1) / k = H(P) + 1/k bitów.

Kompresja a wydajność Wniosek Używając rozszerzonych kodów Huffmana dla coraz większych k osiągamy kompresję coraz bliższą entropii. Ale związane są z tym koszty: n W k-tym rozszerzeniu alfabetu o rozmiarze n uzyskujemy alfabet rozmiaru nk (wzrost wykładniczy!) n Oznacza to wykładniczy wzrost czasu tworzenia kodu n. . . oraz wykładniczy wzrost pamięci potrzebnej na przechowywanie (drzewa) kodu n Ale czas kompresji/dekompresji pozostaje liniowy! W praktyce: Trzeba wybrać kompromis między kompresją a czasem/pamięcią Problem techniczny: tekst musi mieć długość podzielną przez k.

Skąd brać prawdopodobieństwa? Prawdopodobieństwa ustalone z góry, w oparciu o specyfikę danych: n – – z góry znane koderowi i dekoderowi (np. standard wideo H. 263) ale przestaje działać gdy zmieni się charakterystyka danych Wyznaczamy prawdopodobieństwa w oparciu o częstość występowania symboli w kodowanym tekście: n – – konieczne 2 przebiegi: najpierw zliczanie częstości, potem kodowanie konieczne dołączenie kodu lub częstości do zakodowanych danych (dekoder ich nie zna!) Kodowanie dynamiczne: n – – – w każdym kroku korzystamy z częstości w dotychczas zakodowanej części tekstu (znać ją będzie też dekoder) wystarczy jeden przebieg nie trzeba dołączać kodu ani prawdopodobieństw (pbb) do danych.

Dynamiczne kody Huffmana. . . czyli wystarczy tylko raz policzyć do nieskończoności Idea: Przy kodowaniu każdej litery stosujemy kod Huffmana dla pbb opartych na częstościach już zakodowanej części Prawdopodobieństwa te znane są również dekoderowi: n n – n n Przy odkodowywaniu p-tej litery znane są już litery od pierwszej do (p-1)-szej Po każdej literze konieczne modyfikowanie (drzewa) kodu ALE wystarczy jeden przebieg kodowanego pliku! CEL: n Przebudowa kodu po każdym kroku nie powinna być kosztowna!

Dynamiczne kody Huffmana Ważne n przy kodowaniu modyfikujemy kod po zakodowaniu symbolu n przy dekodowaniu modyfikujemy kod przed odkodowaniem symbolu W ten sposób koder i dekoder przy każdym symbolu używają tego samego drzewa kodu!

Dynamiczne kody Huffmana Numerowanie wierzchołków drzewa: n od dołu do góry n od lewej do prawej 7 6 A 5 3 B 4 C 1 D 2

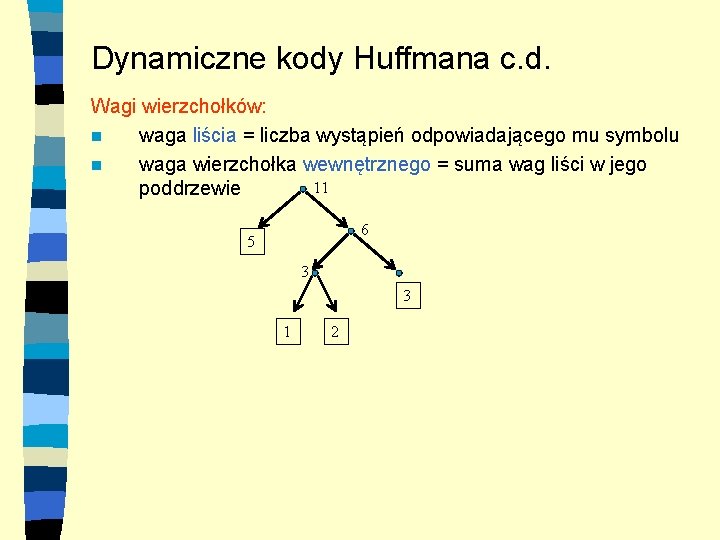
Dynamiczne kody Huffmana c. d. Wagi wierzchołków: n waga liścia = liczba wystąpień odpowiadającego mu symbolu n waga wierzchołka wewnętrznego = suma wag liści w jego 11 poddrzewie 6 5 3 3 1 2

Niezmiennik W optymalnym drzewie kodu dla n symboli istnieje numerowanie wszystkich wierzchołków v 1, , v 2 n-1 spełniające warunki: n w(v 1) w(v 2 n-1), gdzie w(x) to waga wierzchołka x n wierzchołki mające wspólnego rodzica mają sąsiednie numery I na odwrót: Jeśli drzewo kodu ma numerowanie spełniające powyższe warunki, kod jest optymalny Obserwacja: W kodzie Huffmana taką numerację można uzyskać poprzez numerowanie (od końca) w kolejności usuwania elementów (poprzez zsumowanie ich prawdopodobieństw) CEL: zachowywać tę własność w kodowaniu dynamicznym, bez przebudowywania całego drzewa.

Niezmiennik silniejszy Przypomnijmy W optymalnym drzewie kodu dla n symboli istnieje numerowanie wszystkich wierzchołków v 1, , v 2 n-1 spełniające warunki: n w(v 1) w(v 2 n-1), gdzie w(x) to waga wierzchołka x n wierzchołki mające wspólnego rodzica mają sąsiednie numery I na odwrót: Jeśli drzewo kodu ma numerowanie spełniające powyższe warunki, kod jest optymalny Dla nas interesujące jest tylko to, że powyższe własności zachodzą dla numerowania, które sobie zdefiniowaliśmy: n od dołu do góry n od lewej do prawej.

Inicjalizacja Na początku (alfabet a 1, …, am): n n drzewo kodu: złożone z jednego wierzchołka NP (od „nie przesłany”) o wadze 0 i numerze 2 m-1; UWAGI: – wierzchołek NP będzie w drzewie symbolizować wszystkie symbole, które jeszcze nie pojawiły się w tekście – numer 2 m-1 dlatego, że będzie 2 m-1 wierzchołków docelowo (m liści) Wszystkich literom przyporządkowujemy kody stałe, wykorzystywane tylko przy pierwszym pojawieniu się danej litery w tekście:

Kody stałe Niech e i r takie, że m = 2 e + r i 0 r < 2 e. Literze ai przyporządkowujemy kod stały: n (e+1) -bitowej reprezentacji liczby i-1 gdy 1 i 2 r n e-bitowej reprezentacji liczby i-r-1 w przeciwnym przypadku. Czyli n n Kod stały równy kodowi o stałej długości równej log m, gdy m jest potęgą dwójki Mała optymalizacja kodu o stałej długości, gdy m nie jest potęgą dwójki: – 2 r symboli ma kod o długości log m – m - 2 r symbol ma kod o długości log m

Kody stałe - przykład Niech m = 10 (alfabet ma 10 symboli). Wtedy : 10 = 23+2, czyli n e=3 n r=2 Inaczej: rysujemy drzewo o głębokości e+1 i staramy się wykorzystać „wolne” liście (dwa liście na poziomie e+1 dpowiadają jednemu wierzchołkowi na poziomie e) Litera Kod A 1 0000 A 2 0001 A 3 0010 A 4 0011 A 5 010 A 6 011 A 7 100 A 8 101 A 9 110 A 10 111 FAKT: kod stały jest kodem prefiksowym (ćw. )

Kodowanie Dla kolejnego symbolu tekstu b: n jeśli w drzewie kodu nie ma liścia o etykiecie b, kodujemy b jako: – kod wierzchołka NP – a za nim kod stały odpowiadający symbolowi b Dodaj 2 dzieci wierzchołka NP (o numerze p) – lewe dziecko to nowy NP (numerze p-2, waga 0) – prawe dziecko ma etykietę b (numer p-1, waga 1) n n Jeśli w drzewie kodu jest liść o etykiecie b: – kodujemy b za pomocą odpowiadającego mu w drzewie kodu słowa kodowego wykonaj aktualizację drzewa kodu

Dekodowanie Dopóki nie ma końca zakodowanego pliku: n odkoduj słowo kodowe odpowiadające liściowi aktualnego drzewa kodu n jeśli odkodowane słowo kodowe odpowiada literze alfabetu: zapisz ją. n jeśli odkodowane słowo kodowe odpowiada wierzchołkowi NP: – odkoduj kolejną literę według kodu stałego (e lub e+1 bitów według drzewa kodu stałego): zapisz ją. Następnie, dodaj 2 dzieci wierzchołka NP (o numerze p) – lewe dziecko to nowy NP (numerze p-2, waga 0) – prawe dziecko ma etykietę b (numer p-1, waga 1) n wykonaj aktualizację drzewa kodu.

Aktualizacja drzewa kodu CEL - zachowanie niezmiennika: numerowanie wszystkich wierzchołków v 1, , v 2 n-1 (od dołu do góry, od lewej do prawej) ma spełniać warunek: n w(v 1) w(v 2 n-1), gdzie w(x) to waga wierzchołka x Idea rozwiązania: n przechodzimy ścieżkę od liścia odpowiadającego ostatniemu symbolowi i zwiększamy wagi wszystkich wierzchołków o 1 n gdy zwiększenie wagi zaburza powyższy niezmiennik, zamieniamy aktualny wierzchołek z najwyżej położonym wierzchołkiem o takiej samej wadze. Efekt: koszt proporcjonalny do długości słowa kodowego a nie n log n. .

Aktualizacja drzewa kodu c. d. Blok: n zbiór wierzchołków o tej samej wadze. UWAGI: n Jeśli numeracja v 1, , v 2 n-1 spełnia warunek w(v 1) w(v 2 n-1), to wszystkie wierzchołki z jednego bloku tworzą spójny obszar w tej numeracji Jak reprezentujemy bloki: n lista dwustronna w kolejności odpowiadającej numeracji wszystkich wierzchołków n dodatkowo wskaźniki na początki bloków

Aktualizacja drzewa kodu c. d. Niech v to wierzchołek odpowiadający ostatnio zakodowanemu bądź odkodowanemu symbolowi: Dopóki v jest różny od korzenia: n jeśli numer v nie jest największy w bloku do którego v należy: zamień v z wierzchołkiem w o największym numerze w bloku (o ile w nie jest rodzicem v). UWAGI: – zamieniamy całe poddrzewa – v i w zamieniają się numerami – ale numery pozostałych wierzchołków nie zmieniają się n zwiększ wagę v o jeden: w(v)+1 n v rodzic(v)

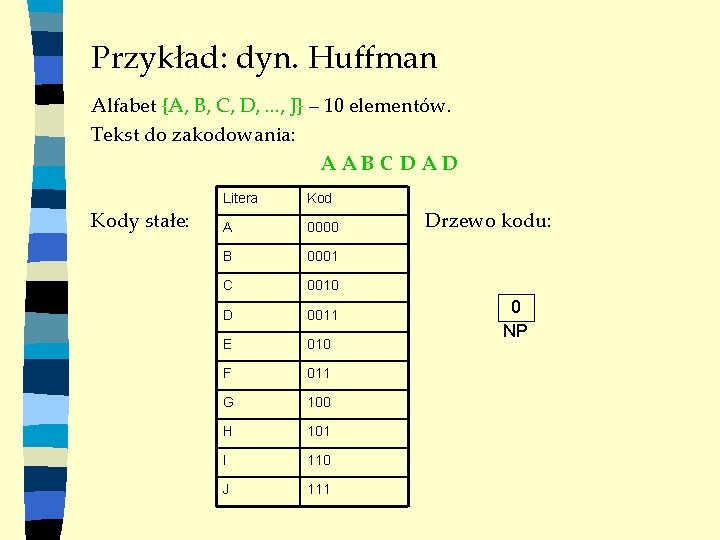
Przykład: dyn. Huffman Alfabet {A, B, C, D, . . . , J} – 10 elementów. Tekst do zakodowania: AABCDAD Kody stałe: Litera Kod A 0000 B 0001 C 0010 D 0011 E 010 F 011 G 100 H 101 I 110 J 111 Drzewo kodu: 0 NP

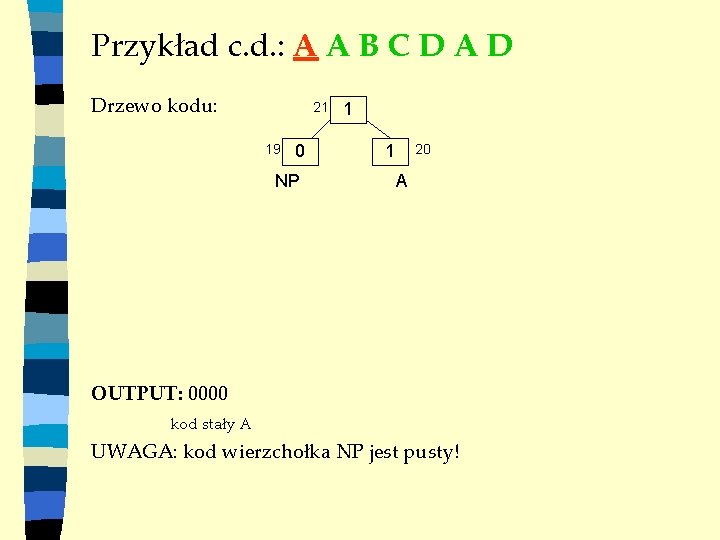
Przykład c. d. AABCDAD Drzewo kodu: 21 0 NP OUTPUT: 0000 kod stały A UWAGA: kod wierzchołka NP jest pusty!

Przykład c. d. : A A B C D A D Drzewo kodu: 21 19 0 NP 1 1 20 A OUTPUT: 0000 kod stały A UWAGA: kod wierzchołka NP jest pusty!

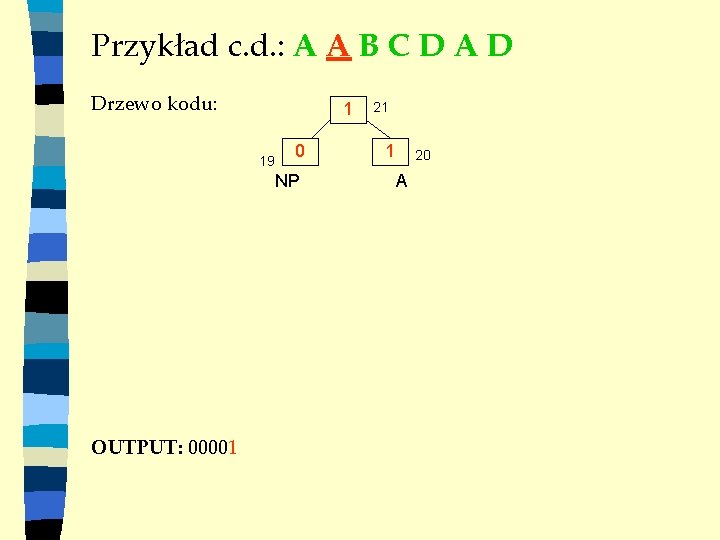
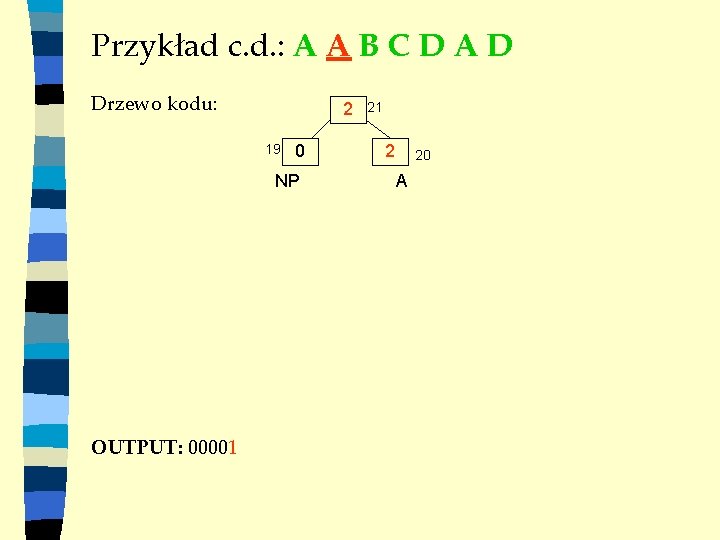
Przykład c. d. : A A B C D A D Drzewo kodu: 1 19 0 NP OUTPUT: 00001 21 1 20 A

Przykład c. d. : A A B C D A D Drzewo kodu: 2 19 0 NP OUTPUT: 00001 21 2 20 A

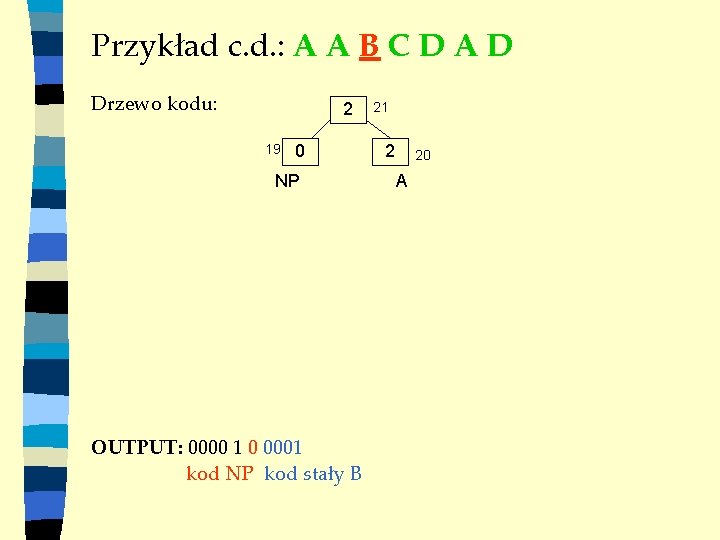
Przykład c. d. : A A B C D A D Drzewo kodu: 2 19 0 NP OUTPUT: 0000 1 0 0001 kod NP kod stały B 21 2 20 A

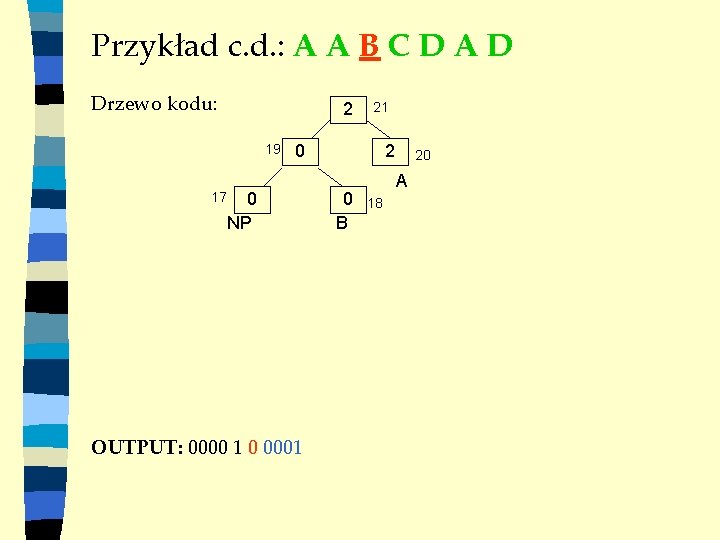
Przykład c. d. : A A B C D A D Drzewo kodu: 2 19 17 21 0 0 NP OUTPUT: 0000 1 0 0001 2 0 B 20 A 18

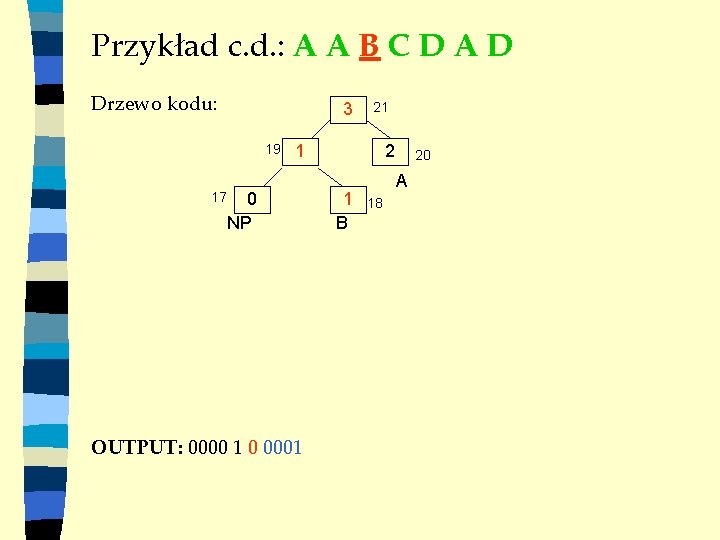
Przykład c. d. : A A B C D A D Drzewo kodu: 3 19 17 21 1 0 NP OUTPUT: 0000 1 0 0001 2 1 B 20 A 18

Przykład c. d. : A A B C D A D Drzewo kodu: 3 19 17 0 NP 21 1 2 1 B 20 A 18 OUTPUT: 0000 1 0 0001 00 0010 kod NP kod stały C

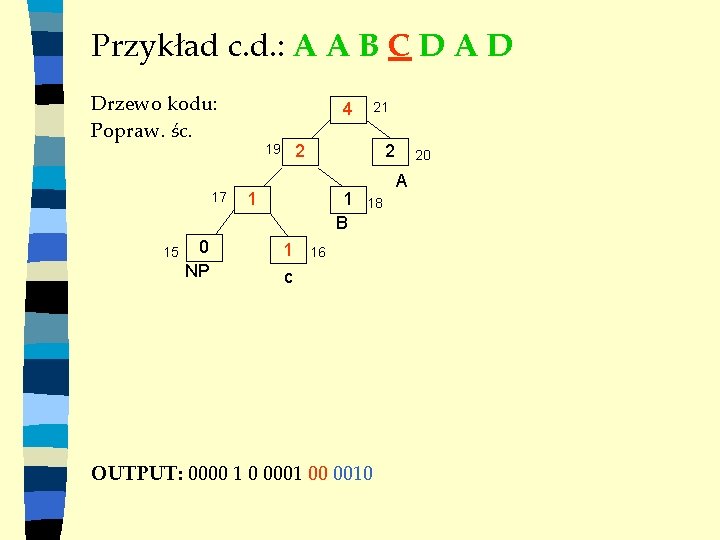
Przykład c. d. : A A B C D A D Drzewo kodu: 3 1 19 17 15 0 NP 21 2 0 1 B 0 c 20 A 18 16 OUTPUT: 0000 1 0 0001 00 0010

Przykład c. d. : A A B C D A D Drzewo kodu: Popraw. śc. 17 15 0 NP 4 21 2 19 2 1 1 B 1 c 20 A 18 16 OUTPUT: 0000 1 0 0001 00 0010

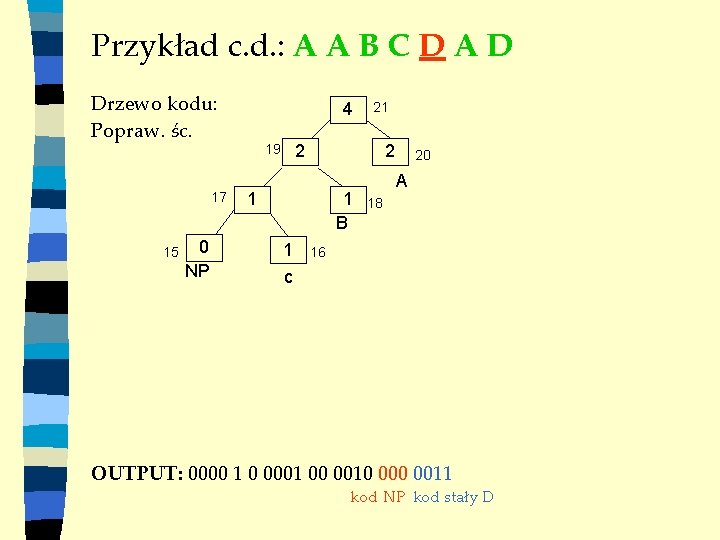
Przykład c. d. : A A B C D A D Drzewo kodu: Popraw. śc. 17 15 0 NP 4 21 2 19 2 1 1 B 1 c 20 A 18 16 OUTPUT: 0000 1 0 0001 00 0010 0011 kod NP kod stały D

Przykład c. d. : A A B C D A D Drzewo kodu: 4 2 19 15 13 0 NP 2 1 17 1 B 0 1 c 0 D 21 20 A 18 16 14 OUTPUT: 0000 1 0 0001 00 0010 0011

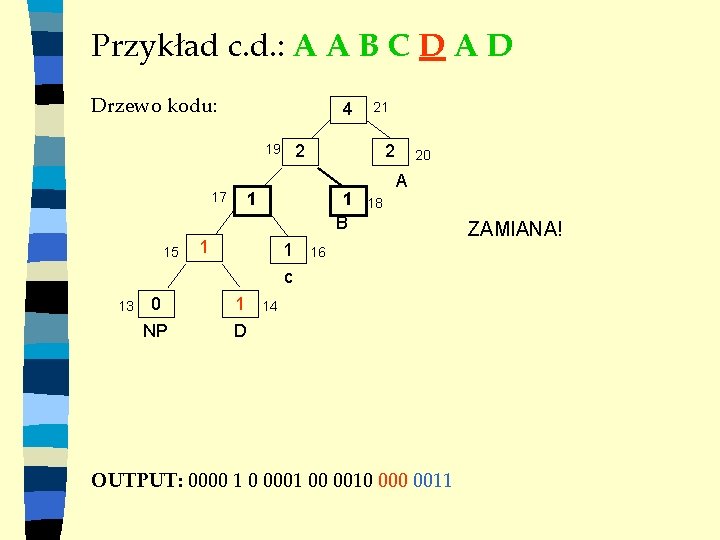
Przykład c. d. : A A B C D A D Drzewo kodu: 4 2 19 15 13 0 NP 2 1 17 1 B 1 1 c 1 D 21 20 A 18 16 14 OUTPUT: 0000 1 0 0001 00 0010 0011 ZAMIANA!

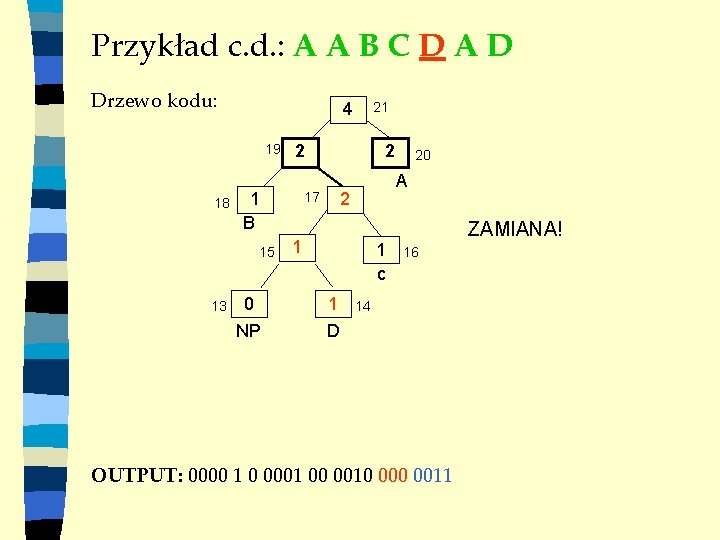
Przykład c. d. : A A B C D A D Drzewo kodu: 4 19 18 13 2 1 B 15 0 NP 21 2 A 2 17 1 1 c 1 D 20 ZAMIANA! 16 14 OUTPUT: 0000 1 0 0001 00 0010 0011

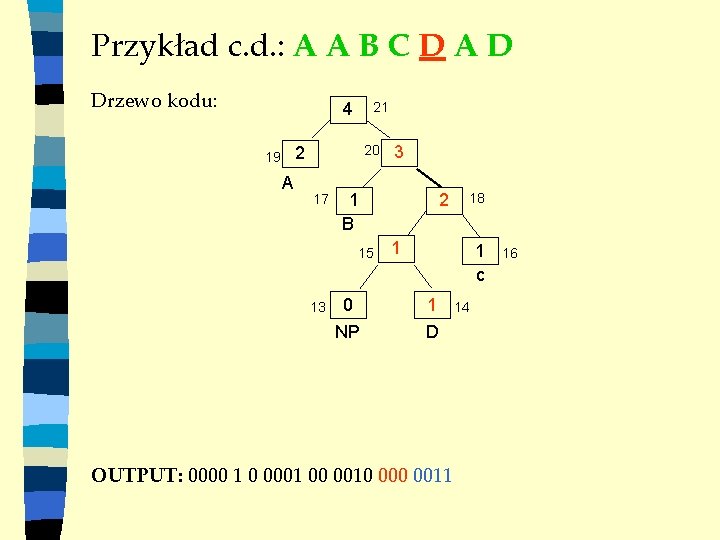
Przykład c. d. : A A B C D A D Drzewo kodu: 4 21 20 2 19 A 17 1 B 15 13 3 0 NP 2 18 1 1 c 1 D OUTPUT: 0000 1 0 0001 00 0010 0011 14 16

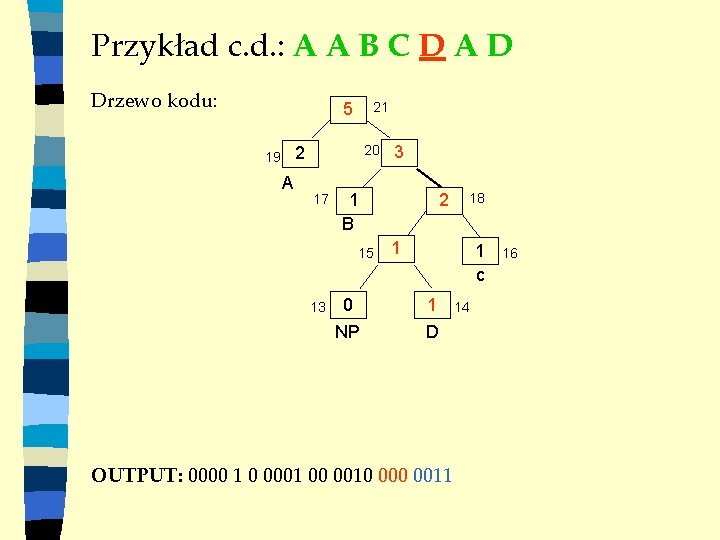
Przykład c. d. : A A B C D A D Drzewo kodu: 5 21 20 2 19 A 17 1 B 15 13 3 0 NP 2 18 1 1 c 1 D OUTPUT: 0000 1 0 0001 00 0010 0011 14 16

Przykład c. d. : A A B C D A D Drzewo kodu: 5 21 20 2 19 A 17 1 B 15 13 3 0 NP 2 18 1 1 c 1 D 16 14 OUTPUT: 0000 1 0 0001 00 0010 0011 0 Uwaga: A był kodowany jako 0000, 1 a na końcu jako 0.

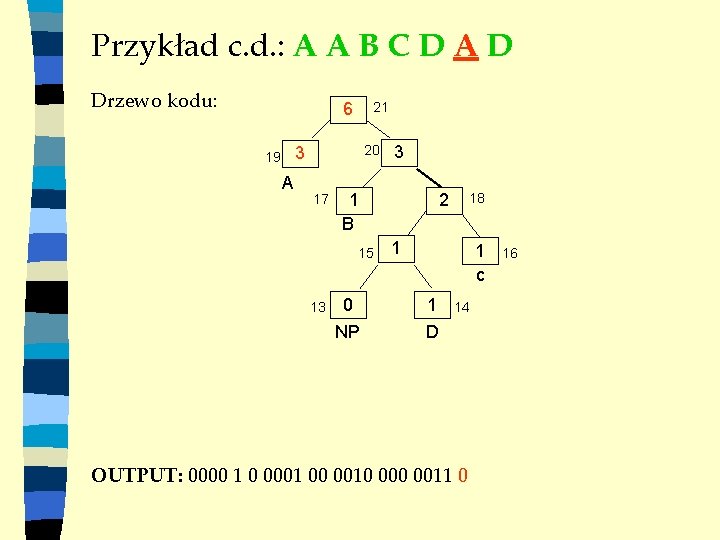
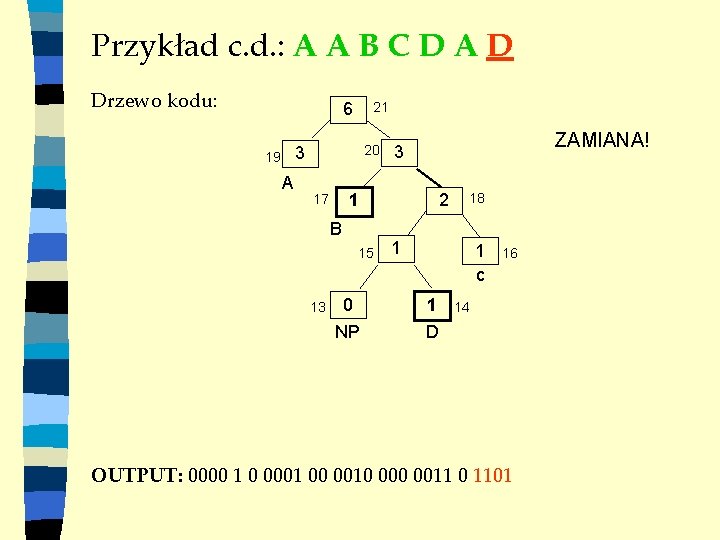
Przykład c. d. : A A B C D A D Drzewo kodu: 6 21 20 3 19 A 17 1 B 15 13 3 0 NP 2 18 1 1 c 1 D 14 OUTPUT: 0000 1 0 0001 00 0010 0011 0 16

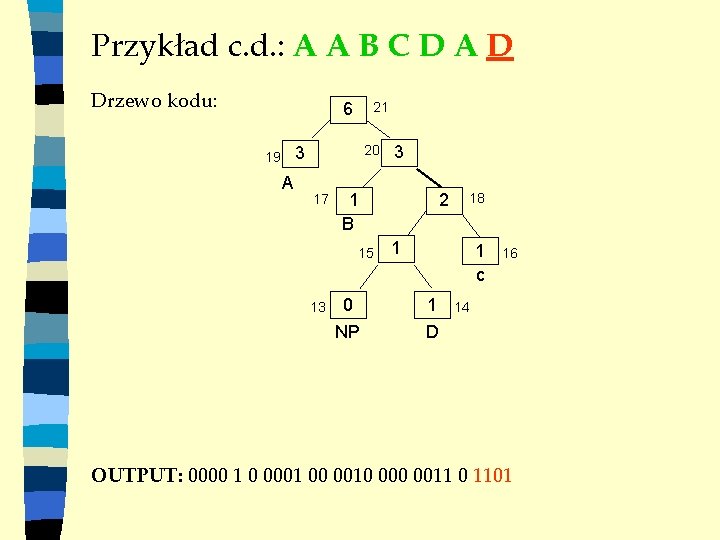
Przykład c. d. : A A B C D A D Drzewo kodu: 6 21 20 3 19 A 17 1 B 15 13 3 0 NP 2 18 1 1 c 1 D 16 14 OUTPUT: 0000 1 0 0001 00 0010 0011 0 1101

Przykład c. d. : A A B C D A D Drzewo kodu: 6 21 20 3 19 A 1 17 B 15 13 ZAMIANA! 3 0 NP 2 18 1 1 c 1 D 16 14 OUTPUT: 0000 1 0 0001 00 0010 0011 0 1101

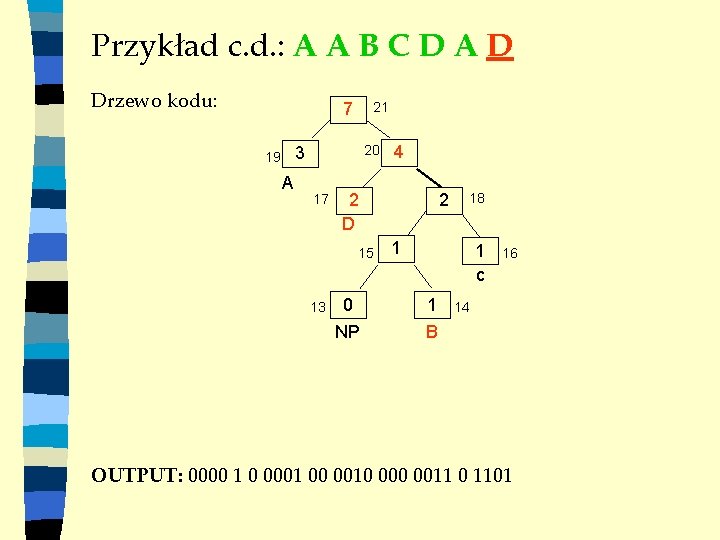
Przykład c. d. : A A B C D A D Drzewo kodu: 7 21 20 3 19 A 17 2 D 15 13 4 0 NP 2 18 1 1 c 1 B 16 14 OUTPUT: 0000 1 0 0001 00 0010 0011 0 1101

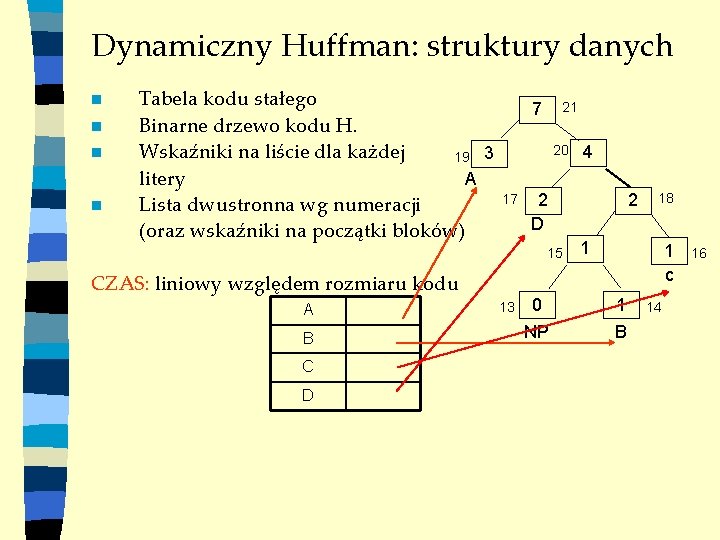
Dynamiczny Huffman: struktury danych n n Tabela kodu stałego Binarne drzewo kodu H. Wskaźniki na liście dla każdej 19 3 litery A Lista dwustronna wg numeracji (oraz wskaźniki na początki bloków) 7 21 20 17 2 D 15 CZAS: liniowy względem rozmiaru kodu A B C D 13 4 0 NP 2 18 1 1 c 1 B 14 16

Dynamiczny Huffman: niezmiennik? Chcemy pokazać, że algorytm modyfikacji drzewa kodu zachowuje własności: n Numeracja w algorytmie v 1, , v 2 n-1 jest numeracją od dołu do góry i od lewej do prawej n Wagi wierzchołków spełniają warunek: w(v 1) w(v 2 n-1) Szkic dowodu: n Zamiana z największym w bloku gwarantuje, że zanim zwiększymy wagę wierzchołka, „wypchniemy” go przed wszystkie wierzchołki, których waga stanie się mniejsza (czyli „na początek” jego bloku) n Ale razem z wierzchołkiem „przestawiamy” całe jego poddrzewo. . . co może zaburzyć numerację n Jednak: wszystkie wierzchołki pomiędzy dwoma zamienianymi są liśćmi (poza jednym przypadkiem. . . )

Kodowanie Huffmana: podsumowanie Własności n Optymalny wśród prefiksowych n Kodowanie i dekodowanie w czasie liniowym! n Kody rozszerzone: kompromis między zasobami a kompresją n Możliwość implementacji jednoprzebiegowej, dynamicznej: kompresja zbliżona do kodu statycznego, dodatkowy czas liniowy Zastosowania: n pk. ZIP, lha, gz, zoo, arj. formaty JPEG i MPEG (jako jeden z etapów, czasem zmodyfikowany) Eksperymenty n Bezstratna kompresja obrazów: współczynnik 1, 5 n Kompresja tekstów w języku naturalnym: wsp. 2 n Kompresja dźwięku: wsp. 1, 5 (kodowanie różnic)

Jak robiono to dawniej. . . Kody Shannona. . . czyli nierówność Krafta jest konstruktywna: n n p 1 … pn to prawdopodobieństwa symboli Fi = p 1 + p 2 +. . . + pi-1 Kod: n Słowo kodowe symbolu ai to pierwszych li = log (1/pi) bitów (``po przecinku'') w binarnej reprezentacji liczby Fi. Ale: n Pokazaliśmy wcześniej, że kod o takich długościach ma średnią długość co najwyżej H(p 1, …, pn )+1

Jak robiono to dawniej. . . Trzeba tylko pokazać, że: Kod Shannona jest kodem prefiksowym. Dowód (szkic): n Fi+1 – Fi = pi 1 / 2 l_i oraz li+1 li gwarantuje, że słowa kodowe coraz dłuższe a różnica między kodem ai i kodem aj dla j > i musi wystąpić wśród pierwszych li pozycji. Do tego tematu wrócimy. . .

Jak robiono to dawniej. . . dziel i zwyciężaj Kod Shannon-Fano v 1. 0. 0: Niech p 1 … pn to prawdopodobieństwa symboli n Jeśli n = 1, to kod(a 1)=0. n Jeśli n=2, to kod(a 1)=0, kod(a 2)=1. n Jeśli n > 2 : – podziel ciąg {p 1, . . . , pn} na dwa podciągi R = {p 1, . . . , pn 1} i S={pn 1+1, . . . , p n} takie, że różnica |(p 1+. . . +pn 1) – (pn 1+1+. . . +pn)| jest minimalna. n Rekurencyjnie, znajdź kody Shannon-Fano dla prawdopodobieństw p 1, . . . , pn 1 oraz pn 1+1, . . . , pn n Poprzedź kody symboli z S bitem 0, kody symboli z R, bitem 1.

Jak robiono to dawniej. . . dziel i zwyciężaj Kod Shannon-Fano v 1. 0. 1 Niech p 1 … pn to prawdopodobieństwa symboli – Wybieramy nie punkt podziału w uporządkowanym ciągu p 1, . . . , pn lecz podział zbioru {p 1, . . . , pn} na dwa podzbiory dające minimalną różnicę sum prawdopodobieństw