Komplekse tall Naturlige tall De frste typer tall

Komplekse tall Naturlige tall De første typer tall vi lærer om er de såkalte naturlige tall: 1, 2, 3, 4, …. Av og til regner også tallet 0 med blant de såkalte naturlige tall: 0, 1, 2, 3, 4, … Mengden av alle naturlige tall betegner vi med N (eller N 0 hvis 0 er med) Vi visualiserer ofte disse tallene ved å plassere dem på en såkalt tall-linje: 0 1 2 3 4 5 6 7 … La oss tenke oss at vi har et vilkårlig naturlig tall n. Adderer vi tallet 1 til n, får vi tallet n + 1 som er større enn n. Det finnes altså ikke noe største naturlige tall.

Komplekse tall Hele tall Vi utvider våre naturlige tall ved å ta med tilhørende negative heltall. Vi får da en tallmengde som vi kaller for hele tall: …, -3, -2, -1, 0, 1, 2, 3, … Mengden av alle hele tall betegner vi med Z. Vi visualiserer ofte disse tallene ved å plassere dem på en såkalt tall-linje: … -3 -2 -1 0 1 2 Eksempler på bruk av negative tall: - Representasjon av kuldegrader på et termometer - Underskudd på konto -… 3 …

Komplekse tall Rasjonale tall (brøker) Vi utvider våre hele tall ved å ta med alle brøker. Merk at alle heltall kan skrives som en brøk (eks: 2 = 2/1). Mengden av alle brøker kaller vi for rasjonale tall og benytter betegnelsen Q. Hvis vi har to gitte brøker p og q, så kan vi alltid finne en brøk som ligger mellom disse to, nemlig (p + q) / 2. Dermed så ville brøkene bli liggende svært tett på tall-linjen. p q (p + q) / 2 0 1/8 Eksempler på bruk av brøk: I et selskap har vi 8 personer og 1 bløtkake. Hvis kaken deles likt, får hver person 1 / 8 kake 1

Komplekse tall Irrasjonale tall Det finnes tall på den reelle tall-linje som ikke kan skrives som en brøk, dvs tall som ikke er rasjonale tall. Disse tallene kalles for irrasjonale tall. Eksempler på irrasjonale tall: 0 1 2 3 4 5 Bevis for at kvadratroten av 2 er et irrasjonalt tall: Eksempler på bruk av irrasjonale tall: Areal av en sirkel 6 7 …

Komplekse tall Irrasjonale tall Bevis for at er et irrasjonalt tall: 1 Vi har et kvadrat med side 1. I følge Pythagoras vil da diagonalen ha lengde 1 Anta at kan skrives som et rasjonalt tall. Vi skal vise at dette fører til en selvmotsigelse. Dette følger av figuren. Altså er ikke et helt tall. Vi antar at kan skrives som en brøk. Vi forkorter brøken slik at vi ikke kan forkorte mer mellom a og b. a / b kan ikke være et heltall i følge linjen ovenfor. Vi kvadrerer ligningen ovenfor. Høyresiden kan ikke forkortes og er ikke et heltall. Da har vi at tallet 2 ikke er et heltall, hvilket er en selvmotsigelse.

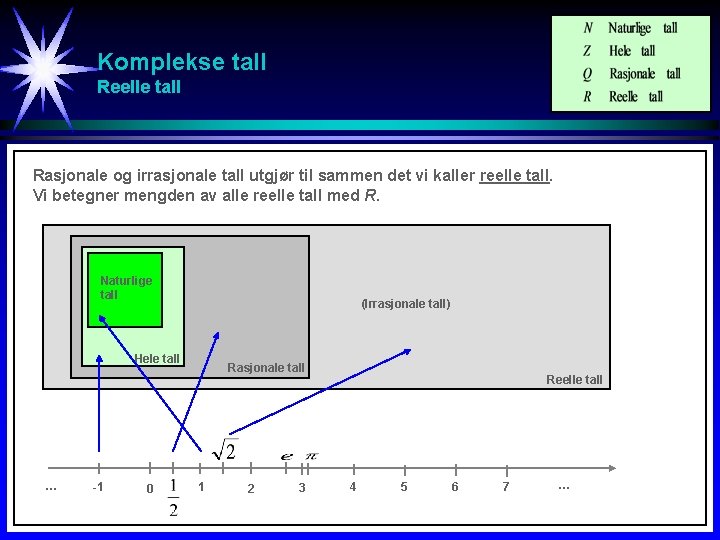
Komplekse tall Reelle tall Rasjonale og irrasjonale tall utgjør til sammen det vi kaller reelle tall. Vi betegner mengden av alle reelle tall med R. Naturlige tall (Irrasjonale tall) Hele tall … -1 0 Rasjonale tall 1 2 3 Reelle tall 4 5 6 7 …

Komplekse tall Reelle tall Tellbare mengder Vi sier at en mengde A er tellbar hvis mengden står i en en-til-en-korrespondanse med mengden av de naturlige tall N, dvs det finnes en bijektiv avbildning mellom A og N. A N Mengden N av alle naturlige tall er tellbar: Det kan vises at mengden Q av alle rasjonale tall er tellbar. Det kan vises at mengden R av alle reelle tall er ikke-tellbar.

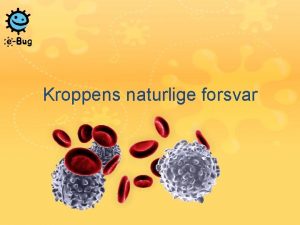
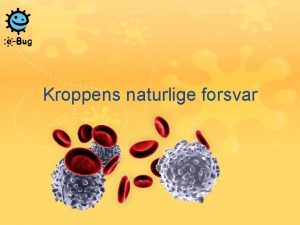
Komplekse tall Reelle tall Intervall L 1 = [0, 1] 0 L 2 = [0, 2] 0 1 2 Der er like mange reelle tall i intervallet L 1 = [0, 1] som det er i intervallet L 2 = [0, 2]. Dette er litt overraskende siden alle elementene i L 1 er inneholdt i L 2 , og det finnes elementer i L 2 som ikke er inneholdt i L 1. Rent intuitivt skulle vi kanske forvente dobbelt så mange elementer i L 2 som i L 1. Det som skaper disse overraskelsene er at disse to mengdene inneholder uendelig mange elementer. Vi må derfor først definere presist hva vi mener med ‘like mange’.

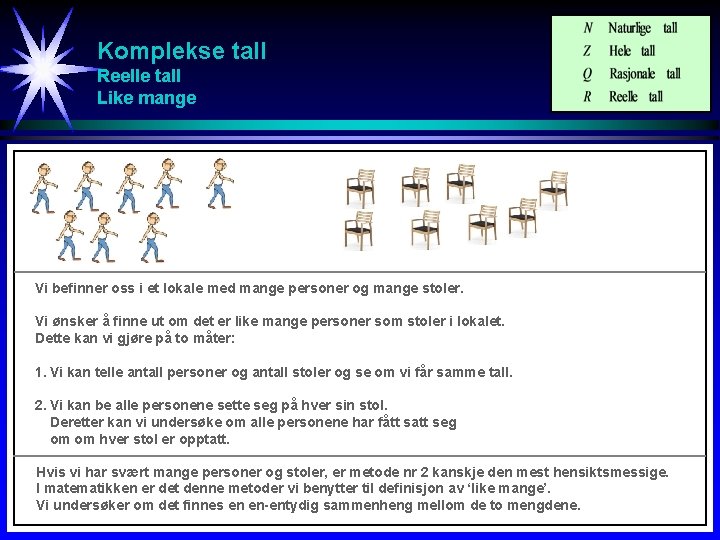
Komplekse tall Reelle tall Like mange Vi befinner oss i et lokale med mange personer og mange stoler. Vi ønsker å finne ut om det er like mange personer som stoler i lokalet. Dette kan vi gjøre på to måter: 1. Vi kan telle antall personer og antall stoler og se om vi får samme tall. 2. Vi kan be alle personene sette seg på hver sin stol. Deretter kan vi undersøke om alle personene har fått satt seg om om hver stol er opptatt. Hvis vi har svært mange personer og stoler, er metode nr 2 kanskje den mest hensiktsmessige. I matematikken er det denne metoder vi benytter til definisjon av ‘like mange’. Vi undersøker om det finnes en en-entydig sammenheng mellom de to mengdene.

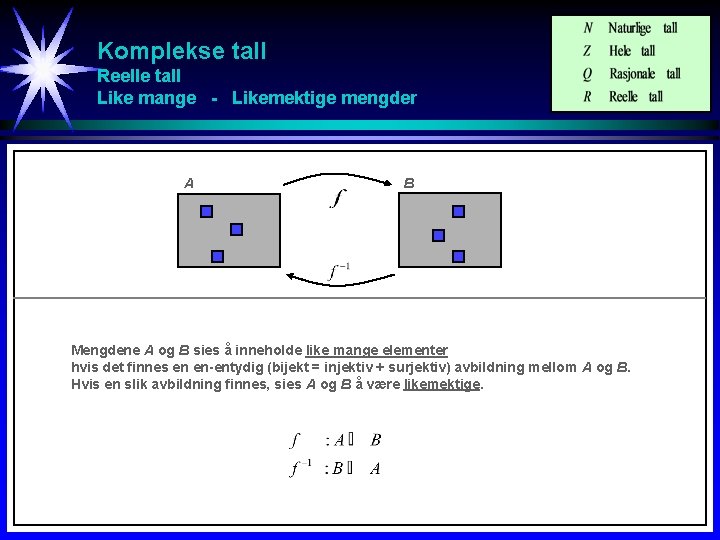
Komplekse tall Reelle tall Like mange - Likemektige mengder A B Mengdene A og B sies å inneholde like mange elementer hvis det finnes en en-entydig (bijekt = injektiv + surjektiv) avbildning mellom A og B. Hvis en slik avbildning finnes, sies A og B å være likemektige.

Komplekse tall Reelle tall Hele tall / Partall … -4 -3 -2 -2 -1 0 0 1 2 2 3 4 … Det finnes like mange hele tall som det finnes partall. Bevis: Følgende funksjon f er en bijektiv avbildning mellom disse to mengdene:

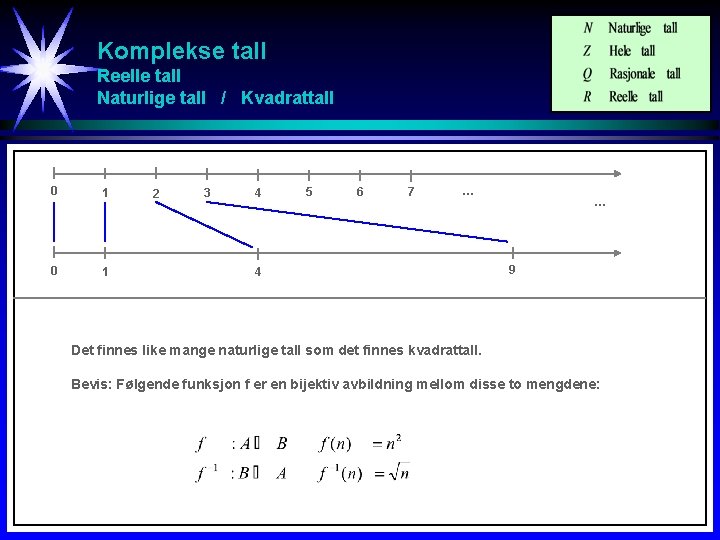
Komplekse tall Reelle tall Naturlige tall / Kvadrattall 0 1 2 3 4 5 6 7 … 4 … 9 Det finnes like mange naturlige tall som det finnes kvadrattall. Bevis: Følgende funksjon f er en bijektiv avbildning mellom disse to mengdene:

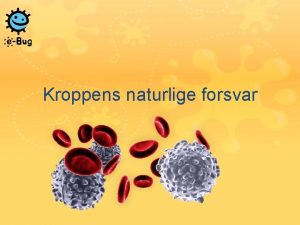
Komplekse tall Reelle tall Intervall [a, b] / Intervall [0, 1] Iab = [a, b] a b I 01 = [0, 1] 0 Det finnes like mange reelle tall i intervallet I 02 = [0, 2] som i intervallet I 01 = [ 0, 1]. 1 Det finnes like mange reelle tall i intervallet Iab = [a, b] som reelle tall i intervallet I 01 = [0, 1]. Bevis: Følgende funksjon f er en bijektiv avbildning mellom disse to mengdene:

Komplekse tall Det finnes oppgaver hvor vi trenger tall som ikke er reelle. Eks: Kloss + Elastisk fjær Siden kvadratrot av negative tall ikke finnes blant de reelle tall, må vi utvide de reelle tallene til såkalte komplekse tall.

Komplekse tall Imaginære tall Komplekst tall Reelle tall Det kan vises at de reelle tallene fyller ut hele den reelle tallinjen. Ved en videre utvidelse må vi derfor benytte en ny dimensjon. for å utvide til såkalte komplekse tall. Mengden av komplekse tall betegnes med C.

Komplekse tall - Ulike notasjoner Imaginære tall Komplekst tall Reelle tall

Komplekse tall - Kompleks konjugering

Komplekse tall - Addisjon

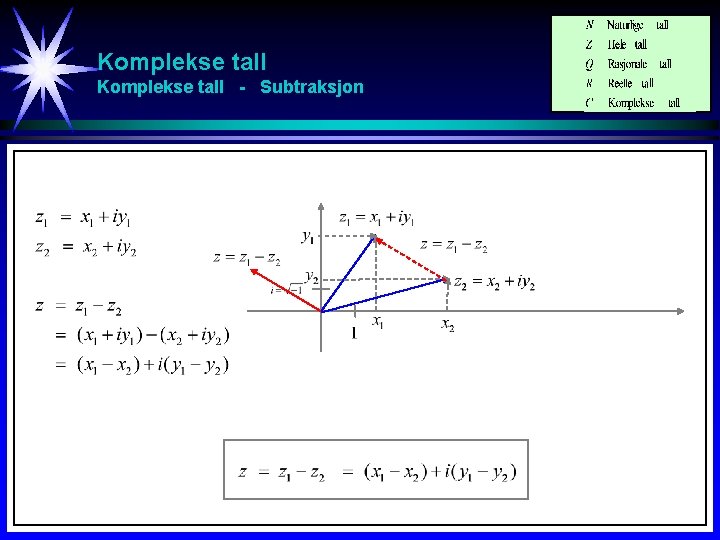
Komplekse tall - Subtraksjon

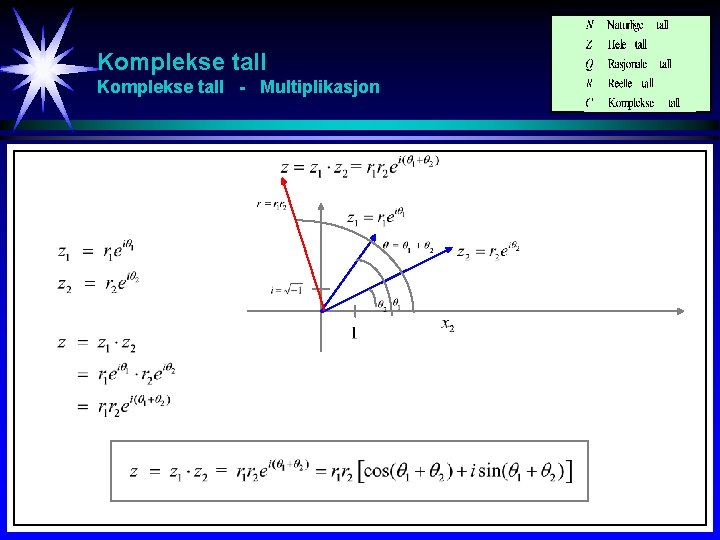
Komplekse tall - Multiplikasjon

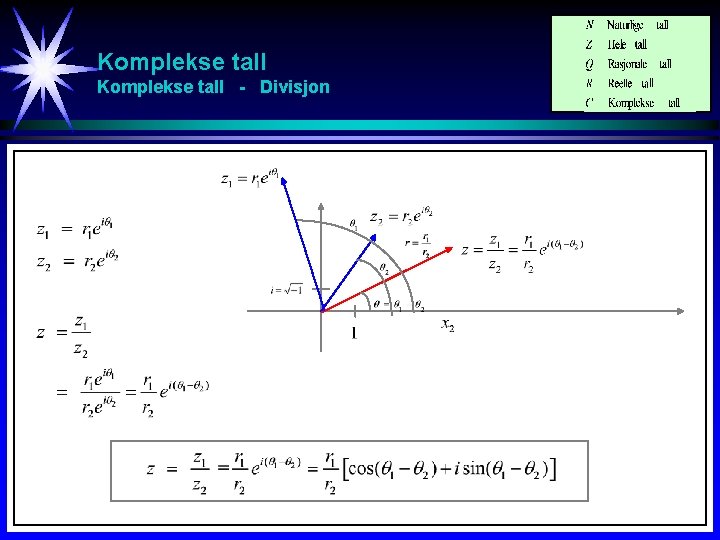
Komplekse tall - Divisjon

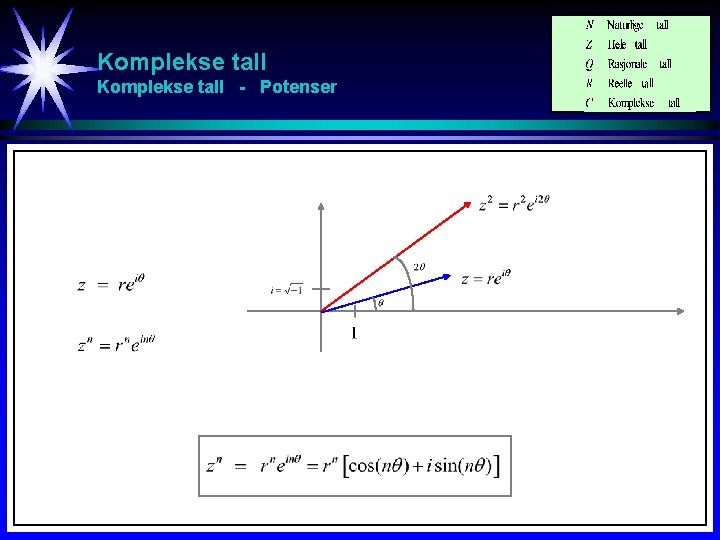
Komplekse tall - Potenser

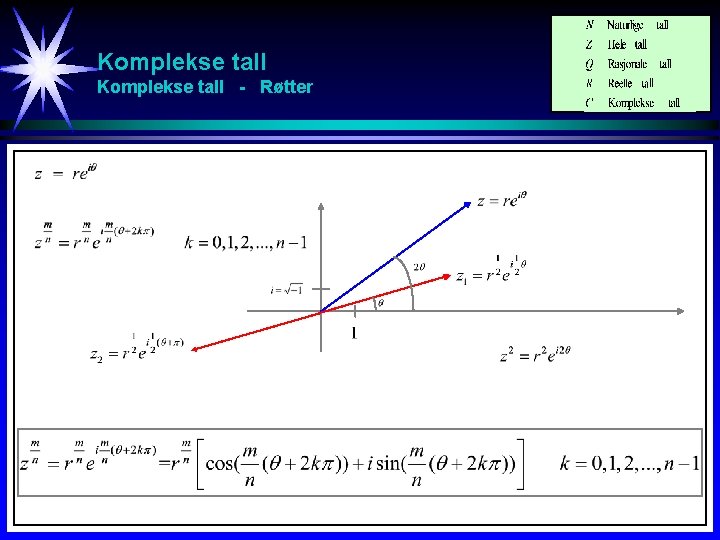
Komplekse tall - Røtter

Komplekse tall - Operasjoner

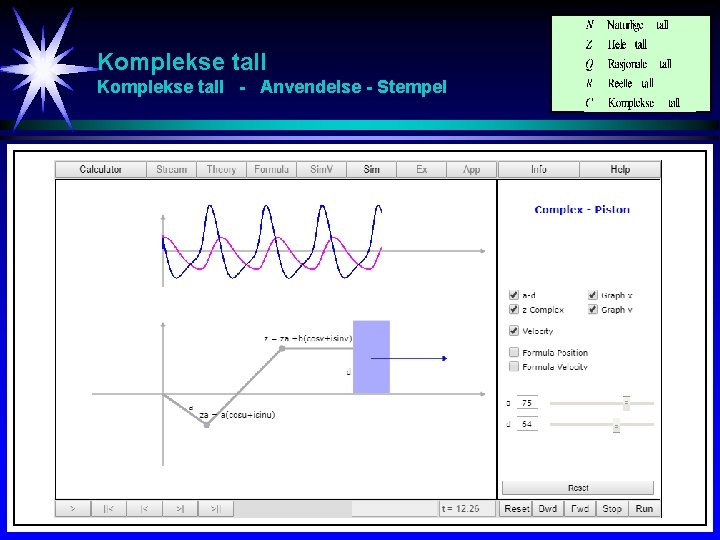
Komplekse tall - Anvendelse - Stempel

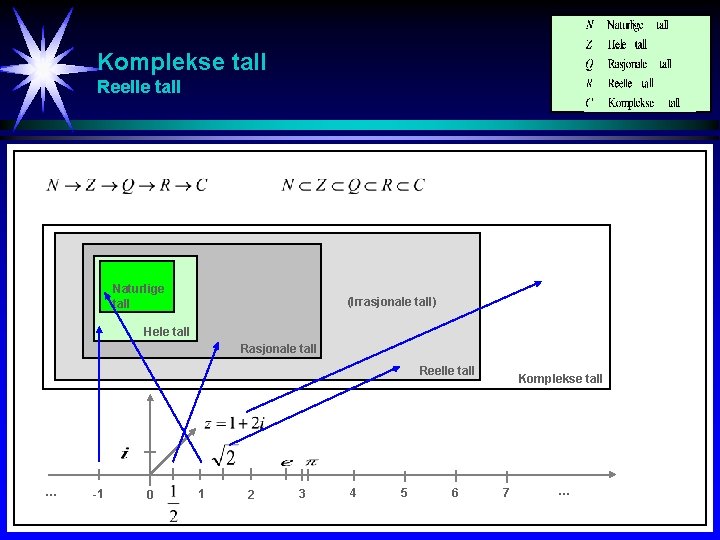
Komplekse tall Reelle tall Naturlige tall (Irrasjonale tall) Hele tall Rasjonale tall Reelle tall … -1 0 1 2 3 4 5 6 Komplekse tall 7 …

END