Koliina informacija Obrada informacija Koliina informacije Poruka moe

Količina informacija Obrada informacija

Količina informacije � Poruka može i ne mora sadržavati informaciju. Na primjer, osoba 'A' posmatra osobu 'B' kako baca kamen u zrak. Osoba 'B' poručuje osobi 'A' da je kamen pao na zemlju. Osobi 'A' poruka ne donosi nova saznanja o događaju, jer oko pada kamena na zemlju nema sumnje. Rezultat događaja osobi 'A' je 100% poznat i vjerovatan, jer drugačije ne može biti. Takva poruka u sebi ne sadrži informaciju. Količina informacije u njoj jednaka je nuli. . 2

� Ako pak osoba 'A' u zrak baci novčić i poruči osobi 'B' da je novčić pao na zemlju na jednu od strana, poruka također ne sadrži informaciju. 50% je moguće da novčić padne na jednu stranu, odnosno 50% je moguće da novčić padne na drugu stranu. Ali poruka da je novčić po padu pokazao 'broj' sadrži novo saznanje o događaju i u sebi sadrži informaciju. Količina informacije u poruci veća je od nule. � Poruka koja tačno opisuje rezultat neizvjesnog događaja, sadrži u sebi određenu količinu informacije. 3

� Claude Shannon (osnivač matematičke teorije informacije) je dokazao da se količina informacije može mjeriti. Jedinica mjerenje količine informacija je 1 BIT. � Bit je minimalna količina za merenje količine informacije. Bit može registrovati samo jednu od dve vrednosti: 0 i 1. � Bajt je veća jedinica za merenje količine informacija. Jedan bajt se sastoji od 8 bitova. � Veće ◦ ◦ jedinice od bajta su: 1 KB=1024 B= 210 B 1 MB = 1024 KB= 220 B 1 GB = 1024 MB= 230 B 1 TB = 1024 GB =240 B �U ovim jedinicama meri se kapacitet memorije računara i veličina fajlova (datoteka). 4

Obrada informacija � Pod obradom podataka možemo smatrati skup aktivnosti koje prevode podatke u oblik koji je upotrebljiv krajnjem korisniku. � Obradu informacija možemo poistovjetiti sa obradom podataka, jer ono što je obični podatak za jednog posmatrača, može biti informacija za drugog posmatrača. � Zajedno sa postupkom obrade informacija, obično se uporedo vrši postupak uskladištavanja (memoriranja) informacija. 5

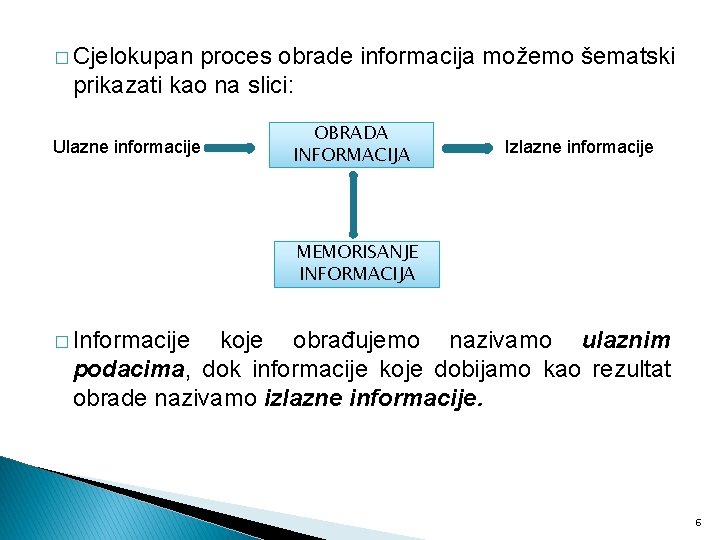
� Cjelokupan proces obrade informacija možemo šematski prikazati kao na slici: Ulazne informacije OBRADA INFORMACIJA Izlazne informacije MEMORISANJE INFORMACIJA � Informacije koje obrađujemo nazivamo ulaznim podacima, dok informacije koje dobijamo kao rezultat obrade nazivamo izlazne informacije. 6

� Obrada informacija je i sastavni dio uobičajenih ljudskih aktivnosti: npr. Učenik dok čita određeni udžbenik, vrši obradu informacija, on prikuplja podatke iz udžbenika, analizira ih, prevodi ih u njemu prihvatljiv oblik i pohranjuje u mozgu za kasniju upotrebu. U ovom slučaju čovjek preuzima ulogu obrađivača informacija. � Takva obrada informacija naziva se ručna (manualna, ljudska) obrada informacija. Ona podrazumjeva obradu informacija uz upotrebu papira, olovke, sveske, pa čak i mašina za pisanje, džepnih kalkulatora. . . ) 7

� Ručna obrada informacija ne može da obradi veliku količinu informacija, spora je i podložna greškama, a pored toga često se oslanja na krajnje monotone i dosadne postupke. Tako se javlja potreba za elektronskom obradom informacija. � Pod elektronskom obradom informacija smatramo upotrebu računara kao sredstva za automatsku obradu podataka. U ovom slučaju ulogu obrađivača informacija preuzima računar. � Računar je svaki uređaj koji je sposoban da prima podatke od korisnika, da ih memoriše i obrađuje prema zadanim uputstvima (programu) i da saopšti rezultate obrade. 8

Osnovne karakteristike elektronske obrade podataka su sljedeće: � Brzina – računar obrađivanje i na stotine miliona instrukcija u sekundi � Repetitivnost – bez zamora i dosade, računar obavlja iste instrukcije milion puta. � Tačnost – računar nikada neće napraviti grešku pod uslovom da su ulazni podaci tačni i program koji vrši obradu tačan. � Pouzdanost- Iako su skloni kvarovima, računari se rijetko kvare a popravke se brzo izvršavaju. � Ekonomičnost- danas su cijene računara relativno niske. 9

� Računar je superiorniji od čovjeka u brzini, jasnoći, preciznosti i količini memorisanih informacija. Ipak, računar ima jednu suštinsku manu u odnosu na čovjeka – teško se snalazi u nepredviđenim situacijama, jer ne posjeduje inteligenciju. Kako se informacije prenose? U vidu signala koje predstavljaju promjene neke fizikalne veličine, najčešće električne prirode. ü Ako je stanje posmatrane veličine poznato u svakom trenutku vremena unutar posmatranog intervala, takve veličine se nazivaju analogne veličine. ü Ukoliko je stanje posmatrane veličine poznato samo u određenim vremenskim trenucima, za takvu veličinu kažemo da je diskretne veličine. 10

� Diskretne veličine koje mogu uzimati samo vrijednosti iz unaprijed određenog i konačnog skupa vrijednosti, nazivaju se digitalne veličine, koje se najčešće predstavljaju u brojčanom obliku uz pomoć cifara. primjer: Razlika analogno - digitalno � Oprema kao što je sat ili merač krvnog pritiska koriste obe vrste prikaza analogni i digitalni prikaz. Npr. sat s digitalnim prikazom pokazuje tačno vreme 8: 23: 15, dok na analognom satu ne možemo videti tačno vreme jer se druga kazaljka uvek kreće. S druge strane, ako želimo videti koliko minuta ostaje do dolaska voza, potrebno je izračunati “vreme dolaska voza – trenutno vreme“ za sat s digitalnim prikazom, međutim sa satom koji ima analogni prikaz, možete vizuelno proceniti koliko je vremena prošlo, a koliko ostalo. 11

BROJNI SISTEMI Pojam i podjela

Brojni sistemi broj≠cifra Ø Broj je vrijednost , a cifra je samo zapis te vrijednosti. Ø Brojevi se predstavljaju pomoću cifara. Ø Brojni sistem je zajednički naziv za skup pravila pomoću kojih se jednoznačno zapisuju brojevi. Pravila opisuju kako se brojevi zapisuju (cifre), kao i kako se zapis tumači. 13

Podjela brojnih sistema � Primjer nepozicionog brojnog sistema je RIMSKI brojni sistem (svojstvo cifre ne zavisi od pozicije na kojoj se nalazi). Npr: rimski brojevi XI i IX �U oba slučaja cifra I ima vrednost 1. 14

Ø Pozicioni brojni sistemi su oni u kojima se težina cifre (njen udeo u celokupnoj vrednosti broja) određuje na osnovu njene pozicije u broju (što veća pozicija, to je veći i udeo u vrednosti broja) Primjer: arapski brojevi Broj 11 ima dve cifre 1 koje su različite težine. Što je pozicija cifre više levo, težina cifre je veća. Ø Pošto većina svijeta danas koristi pozicioni brojni sistem, uz njega usko se veže pojam baze brojnog sistema. Baza brojnog sistema je vrijednost koja se pridružuje pojedinoj cifri u pozicionom brojnom sistemu, zavisno od njenog položaju u zapisu. 15

Najpoznatiji brojni sistemi su: üdekadni-decimalni (baza 10), übinarni (baza 2) üoktalni (baza 8), i üheksadecimalni (baza 16). 16

Dekadni -decimalni brojni sistem � Tradicionalni brojni sistem, koji se izučava u školi, i koji se koristi u svakodnevnom životu, naziva se dekadni (decimalni) brojni sistem. U ovakvom sistemu, broj se predstavlja nizom cifara, a poziciji svake cifre odgovara određena težina. � Dekadni brojni sistem ima bazu 10 i sljedeće cifre: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. 17

Primjer: • Poziciona vrijednost raste idući u levo od zareza za svaku poziciju 10 puta, a opada isto za 10 puta za svaku poziciju desno od zareza. 18

Binarni brojni sistem Ø Sve računarske riječi, kao i sadržaj memorijskih lokacija i registara u računarskim sistemima, mogu se predstaviti pomoću binarnog brojnog sistema. Ø Binarni brojni sistem ima bazu 2 Ø Za formiranje brojeva koriste se sledeće cifre: 0 i 1. � Npr. riječ. 0110010111101100 16 -bitna računarska 19

� Binarne brojeve uvjek izgovaramo cifru po cifru, tj. binarni broj 100 čitamo isključivo “jedan nula” a nikada “sto”. � Današnji digitalni računari sve podatke pamte isključivo kao skupinu brojeva, pri čemu se svaki broj čuva u binarnom zapisu. Primjer: � Binarnom zapisu 100111 ekvivalentna je suma 39 u dekadnom brojnom sistemu, jer je: 20

Oktalni brojni sistem � Oktalni brojni sistem ima bazu 8. � Za formiranje brojeva koristi se 8 cifara: 0, 1, 2, 3, 4, 5, 6, 7. � Svaki broj oktalnog brojnog sistema se može predstaviti kao zbir proizvoda svojih cifara i njihovih pozicionih vrijednosti. Primjer: 21

Hekasadecimalni brojni sistem � Ima bazu 16 i cifre 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E. Navedena slova imaju sljedeće vrijednosti: A = 10, B = 11, C = 12, D = 13, E = 14, F = 15 22

Primjer: Recimo imamo FD 3 (baza 16) što je u dekadnom sistemu 4051. Bitno je uvidjeti da se slova zamjenjuju odgovarajućim vrijednostima! 23

Zadaci za vježbu. . 1. 1863(10)=? 2. 1010(2)=? 3. 251(8)=? 4. B 2 A 4(16)=? 24