KnowledgeBased Support Vector Machine Classifiers NIPS2002 Vancouver December

Knowledge-Based Support Vector Machine Classifiers NIPS*2002, Vancouver, December 9 -14, 2002 Glenn Fung Olvi Mangasarian Jude Shavlik University of Wisconsin-Madison

Outline of Talk v. Support Vector Machine (SVM) Classifiers Ø Standard Quadratic Programming formulation Ø Linear Programming formulation: 1 -norm linear SVM v Polyhedral Knowledge Sets Ø v Knowledge-Based SVMs Ø Incorporating knowledge sets into a classifier v Empirical Evaluation Ø The DNA promoter dataset Ø Wisconsin breast cancer prognosis dataset v Conclusion

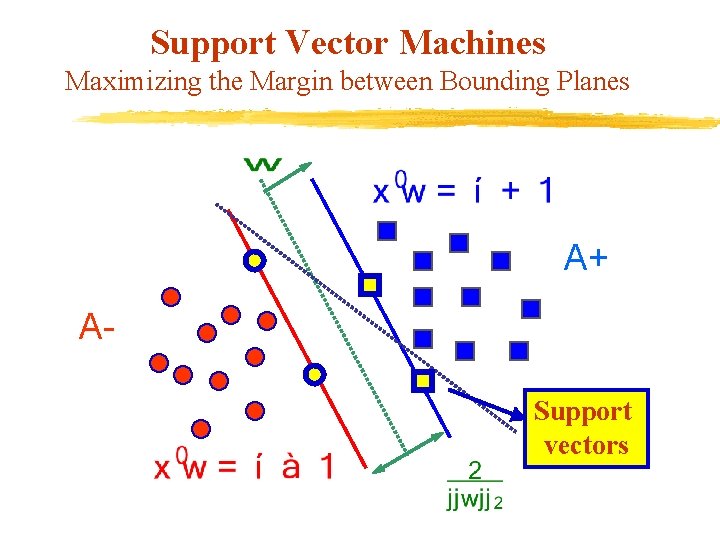
Support Vector Machines Maximizing the Margin between Bounding Planes A+ ASupport vectors

Support Vector Machines Maximizing the Margin between Bounding Planes A+ A-

Algebra of the Classification Problem 2 -Category Linearly Separable Case v Given m points in n dimensional space v Represented by an m-by-n matrix A in class +1 or – 1 specified by: v Membership of each Ø An m-by-m diagonal matrix D with +1 & -1 entries v Separate by two bounding planes, v More succinctly: where e is a vector of ones.

Support Vector Machines Quadratic Programming Formulation v Solve the following quadratic program: min s. t. v Minimize empirical error v Maximize the margin with weight by minimizing

Support Vector Machines Linear Programming Formulation v Use the 1 -norm instead of the 2 -norm: min s. t. v This is equivalent to the following linear program: min s. t.

Knowledge-Based SVM via Polyhedral Knowledge Sets

Incorporating Knowledge Sets Into an SVM Classifier v Suppose that the knowledge set: belongs to the class A+. Hence it must lie in the halfspace : v We therefore have the implication: v Will show that this implication is equivalent to a set of constraints that can be imposed on the classification problem.

Knowledge Set Equivalence Theorem

Proof of Equivalence Theorem ( Via Nonhomogeneous Farkas or LP Duality) Proof: By LP Duality:

Knowledge-Based SVM Classification

Knowledge-Based SVM Classification v Adding one set of constraints for each knowledge set to the 1 -norm SVM LP, we have:

Knowledge-Based LP with Slack Variables Minimize Error in Knowledge Set Constraints Satisfaction

Knowledge-Based SVM via Polyhedral Knowledge Sets

Empirical Evaluation The Promoter Recognition Dataset v Promoter: Short DNA sequence that precedes a gene sequence. v A promoter consists of 57 consecutive DNA nucleotides belonging to {A, G, C, T}. v Important to distinguish between promoters and nonpromoters v This distinction identifies starting locations of genes in long uncharacterized DNA sequences.

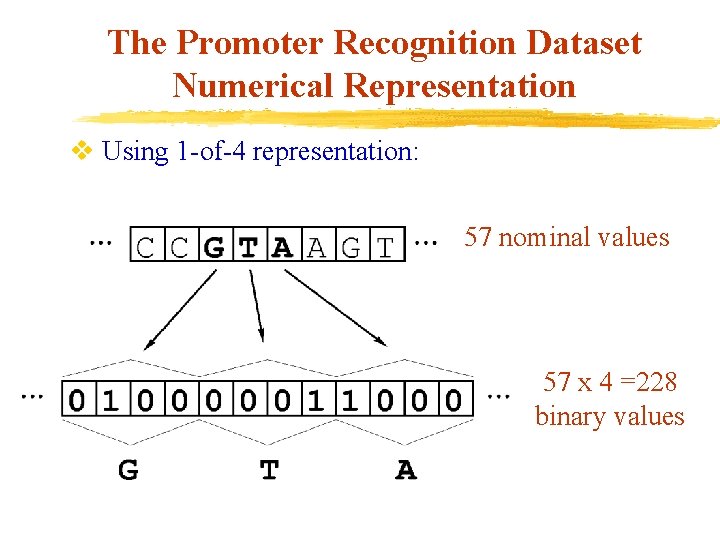
The Promoter Recognition Dataset Numerical Representation v Using 1 -of-4 representation: 57 nominal values 57 x 4 =228 binary values

Promoter Recognition Dataset Prior Knowledge Rules v Prior knowledge consist of the following 64 rules Ri:

Promoter Recognition Dataset Sample Rules A sample rule is:

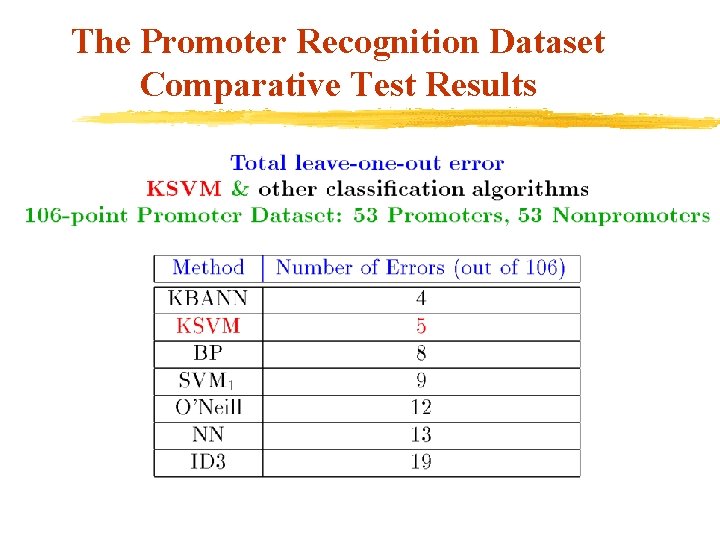
The Promoter Recognition Dataset Comparative Test Results

Wisconsin Breast Cancer Prognosis Dataset Description of the data v 110 instances corresponding to 41 patients whose cancer had recurred and 69 patients whose cancer had not recurred v 32 numerical features v The domain theory: two simple rules used by doctors:

Wisconsin Breast Cancer Prognosis Dataset Numerical Testing Results v Doctor’s rules applicable to only 32 out of 110 patients. v Only 22 of 32 patients are classified correctly by this rule. v. KSVM linear classifier applicable to all patients with correctness of 66. 4%. v Correctness comparable to best available results using conventional SVMs. v KSVM can get classifiers based on knowledge without using any data.

Conclusion v Prior knowledge easily incorporated into classifiers through polyhedral knowledge sets. v Resulting problem is a simple linear program. v Knowledge sets can be used with or without conventional labeled data. v In either case, KSVM is better than most classifiers tested.

Future Research v Generate classifiers based on prior expert knowledge in various fields Ø Diagnostic rules for various diseases Ø Financial investment rules Ø Intrusion detection rules v Extend knowledge sets to general convex sets v Nonlinear kernel classifiers. Challenges: Ø Express prior knowledge nonlinearly Ø Extend equivalence theorem to general convex sets

Web Pages