Knowledge Representation Reasoning Lecture 4 5 Predicate Logic

Knowledge Representation & Reasoning Lecture 4 & 5 : Predicate Logic or First Order Logic (FOL)

2 13/5/2011 TP 2623, shereen@ftsm. ukm. my Motivation Propositional logic is declarative J Propositional logic allows partial/disjunctive/negated information J (unlike most data structures and databases) J Propositional logic is compositional: J meaning of B 1, 1 P 1, 2 is derived from meaning of B 1, 1 and of P 1, 2 J Meaning in propositional logic is context-independent J (unlike natural language, where meaning depends on context) L Propositional logic has very limited expressive power L (unlike natural language) L E. g. , cannot say “pits cause breezes in adjacent squares” except by writing one sentence for each square

3 13/5/2011 TP 2623, shereen@ftsm. ukm. my Predicates and Constants • Let's consider the statements: Mariam is female Johan is male Mary and John are siblings • In propositional logic the above statements are atomic propositions: P = Mariam-is-female Q = Johan-is-male R = Mariam-and-Johan-are-siblings • In FOL atomic statements use predicates, with constants as argument: female(mariam) male(johan) siblings(mariam, johan)

4 13/5/2011 TP 2623, shereen@ftsm. ukm. my Variables and Quantifiers • Let's consider the statements: Everybody is male or female A male is not a female • In FOL predicates may have variables as arguments, whose value is bounded by quantifiers: • x. Male(x) Female(x) • Deduction (why? ): Mariam is not male(mariam)

5 13/5/2011 TP 2623, shereen@ftsm. ukm. my Functions Let’s consider the statement: ▫ The father of a person is male In FOL, objects of the domain may be denoted by functions applied to (other) objects: x. male(father(x))

6 13/5/2011 TP 2623, shereen@ftsm. ukm. my FOL Syntax • User define these primitives ▫ Constant symbols (i. e. the “individuals” in the world), e. g. Mariam, 3 ▫ Function symbols (mapping individuals to individuals), e. g. father-of(mariam)=johan; colour -of(sky)=blue ▫ Predicate symbols (mapping from individuals to truth value), e. g. greater(5, 3), green(grass), colour(grass, green)

7 13/5/2011 TP 2623, shereen@ftsm. ukm. my FOL Syntax • FOL supplies these primitives ▫ Variable symbols. e. g. x, y ▫ Connectives. Same as PL ▫ Quantifiers: Universal ( ) and existential ( ) corresponds to conjunction ( ) corresponds to disjunction ( ) usually used with “implies” to form (if then rules) usually used with “and” to specify a list of properties or facts about an individual Switching the order of does not change the meaning Switching the order of and does change the meaning

8 13/5/2011 Summary of FOL Syntax: Basic Elements • • Constants Predicates Functions Variables Connectives Equality Quantifiers Mariam, 2, UKM, . . . Brother, >, . . . Sqrt, Left. Side. Of, . . . x, y, a, b, . . . , , = , TP 2623, shereen@ftsm. ukm. my

9 13/5/2011 TP 2623, shereen@ftsm. ukm. my Atomic Sentences • Sentences are built from terms and atoms: ▫ A term is a logical expression that refers to an object Term = function (term 1, . . . , termn) or constant or variable ▫ An atomic sentence is an n-place predicate of n terms Atomic sentence = predicate (term 1, . . . , termn) or term 1 = term 2 • A well formed formula (wff) is an atomic sentence containing no free variables, i. e. all variables are “bound” by universal or existential quantifiers.

10 13/5/2011 TP 2623, shereen@ftsm. ukm. my Atomic sentence • Atomic sentence can have complex terms Friend-of(Father(Ahmad), Father(Ali)) Ahmad’s father is a friend of Ali’s father • We can use logical connectives to construct more complex sentences x (Pemandu(x) ⌐Penumpang(x)) Untuk setiap yang menjadi pemandu mereka adalah bukan penumpang x, y (Melatih(x, y) (Jurulatih(x) Pelatih(y))) x, y (Driving. Experience(x, y) (Driver(x) Passenger(y))) Untuk setiap yang melatih orang lain, seorang akan menjadi jurulatih dan seorang lagi menjadi pelatih

11 13/5/2011 TP 2623, shereen@ftsm. ukm. my Universal quantification • <variables> <sentence> Everyone at UKM is smart: x. At(x, UKM) Smart(x) • x P is true in a model m, iff P is true with x being each possible object in the model • Roughly speaking, equivalent to the conjunction of instantiations of P . . . At(Ahmad, UKM) Smart(Ahmad) At(Ali, UKM) Smart(Ali) At(Aminah, UKM) Smart(Aminah)

12 13/5/2011 TP 2623, shereen@ftsm. ukm. my A common mistake to avoid • Typically, is the main connective with • Common mistake: using as the main connective with : x At(x, UKM) Smart(x) means “Everyone is at UKM and everyone is smart”

13 13/5/2011 TP 2623, shereen@ftsm. ukm. my Existential quantification • <variables> <sentence> • Someone at UKM is smart: • x At(x, UKM) Smart(x) • x P is true in a model m, iff P is true with x being some possible object in the model • Roughly speaking, equivalent to the disjunction of instantiations of P At(Ahmad, UKM) Smart(Ahmad) At(Ali, UKM) Smart(Ali) At(Aminah, UKM) Smart(Aminah) . . .

14 13/5/2011 TP 2623, shereen@ftsm. ukm. my Another common mistake to avoid • Typically, is the main connective with • Common mistake: using as the main connective with : x At(x, UKM) Smart(x) is true if there is anyone who is not at UKM! Also means that some people at UKM are smart, but also say that some people who are not at UKM are also smart.

15 13/5/2011 TP 2623, shereen@ftsm. ukm. my Properties of quantifiers • x y is the same as y x • x y is not the same as y x • x y Loves(x, y) ▫ “There is a person who loves everyone in the world” • y x Loves(x, y) ▫ “Everyone in the world is loved by at least one person” • • • Quantifier duality: each can be expressed using the other x Likes(x, Ice. Cream) Everyone likes ice cream There is no one who does not like ice cream x Likes(x, Broccoli) Someone likes broccoli not all people does not like broccoli

16 13/5/2011 TP 2623, shereen@ftsm. ukm. my Equality • term 1 = term 2 is true under a given interpretation if and only if term 1 and term 2 refer to the same object • E. g. , definition of Sibling in terms of Parent: x, y Sibling(x, y) [ (x = y) m, f (m = f) Parent(m, x) Parent(f, x) Parent(m, y) Parent(f, y)]

17 13/5/2011 Translating language to FOL 1. 2. 3. 4. 5. Semua petani suka matahari Semua cendawan ungu adalah beracun Tiada cendawan ungu yang beracun Terdapat dua cendawan ungu Ali tidak tinggi TP 2623, shereen@ftsm. ukm. my

18 13/5/2011 TP 2623, shereen@ftsm. ukm. my Example FOL • Hubungan keluarga ▫ Ibu, suami, isteri, Ibu. Bapa(parent) dll • Ibu kepada individu adalah merupakan Ibu. Bapa perempuan individu tersebut m, c Ibu(c) = m (Perempuan(m) Ibu. Bapa(m, c)) • Lelaki & perempuan adalah hubungan disjoint x Lelaki(x) Perempuan(x) • Ibu. Bapa dan anak adalah hubungan inverse(berbalik) p, c Ibu. Bapa(p, c) Child(c, p) • Datok ialah Ibu. Bapa kepada Ibu. Bapa seorang individu g, c Datok(g, c) p Ibu. Bapa(g, p) ∧ Ibu. Bapa(p, c)

19 13/5/2011 TP 2623, shereen@ftsm. ukm. my Bird Example • • • Every normal bird can fly An ostrich is a bird and not a normal bird A whirlybird is not a bird Every object that is not a bird that is not normal is either a normalbird or a whirlybird Tweety is a bird Tweety is not a normal bird Tweety has her wings clipped There are precisely two individuals that are parents of Tweety, and they are both normal birds.

20 TP 2623, shereen@ftsm. ukm. my 13/5/2011 Interpreting the Bird Example • Domain ▫ {birds whirlybird} • Assign Constants ▫ Tweety • Assign Functions ▫ none • Assign Predicate Symbols ▫ ▫ ▫ ▫ Bird(x) Normal(x) Can-fly(x) Ostrich(x) Whirlybird(x) Clipped-wings(x) Parent(x, Tweety) Equals(x, y) • Every normal bird can fly • An ostrich is a bird and not a normal bird • A whirlybird is not a bird • Every object that is not a bird that is not normal is either a normalbird or a whirlybird • Tweety is a bird • Tweety is not a normal bird • Tweety has her wings clipped • There are precisely two individuals that are parents of Tweety, and they are both normal birds.

21 13/5/2011 Bird Example • Every normal bird can fly x [ (Bird(x) Normal(x)) Can-fly(x) ] • An ostrich is a bird and not a normal bird x [ (Ostrich(x) (Bird(x) Normal (x)) ] • A whirlybird is not a normal bird x [ (Whirlybird(x) (Bird(x) Normal (x) ) ] • A whirlybird is not a bird x [ (Whirlybird(x) Bird(x)) ] TP 2623, shereen@ftsm. ukm. my

22 13/5/2011 TP 2623, shereen@ftsm. ukm. my Bird Example • Every object that is not a bird that is not normal is either a normal bird or a whirlybird x [ (Bird(x) Normal(x)) ((Normal (x) (Bird(x)) Whirlybird(x))] • Tweety is a bird Bird(Tweety) • Tweety is not a normal bird (Normal (Tweety) Bird(Tweety)) • Tweety has her wings clipped Clipped-wings(Tweety)

23 13/5/2011 TP 2623, shereen@ftsm. ukm. my Bird Example • There are precisely two individuals that are parents of Tweety, and they are both normal birds. x y [ Equals(x, y) Parent(x, Tweety) Parent(y, Tweety) [ z (parent(z, Tweety) (equals (z, x) Equals (z, y))) ] ] x [ (Parent(x, Tweety) (normal(x) Bird (x)) ]

24 13/5/2011 TP 2623, shereen@ftsm. ukm. my Exercise Translate the following sentences into FOL 1. Everything is bitter or sweet. (Semua benda adalah pahit atau manis) 2. Either everything is bitter or everything is sweet. (Sama ada semua pahit atau semua benda manis) 3. There is somebody who is loved by everyone. (Ada seseorang yang disukai oleh semua) 4. If someone is noisy, everybody is annoyed. (Jika seseorang bising, maka semua orang lain akan marah)

Inference Rules for FOL

26 13/5/2011 TP 2623, shereen@ftsm. ukm. my Background • Inference rules for PL apply to FOL. For example: modus ponens, and-introduction, andelimination • New rules for use with quantifiers: ▫ Universal instantiation ▫ Existential elimination

27 13/5/2011 TP 2623, shereen@ftsm. ukm. my INFERENCE IN FIRST-ORDER LOGIC • Reducing first-order inference to propositional inference • Unification • First-order inference algorithms ▫ Forward chaining Deductive database and production systems ▫ Backward chaining and logic programming ▫ Resolution-based theorem proving

28 13/5/2011 TP 2623, shereen@ftsm. ukm. my Propositional vs First-Order Inference • Inference rules for quantifiers ▫ Infer the following sentences: King(John) ^ Greedy(John) => Evil(John) King(Richard) ^ Greedy(Richard) => Evil(Richard) King(Father(John)) ^ Greedy(Father(John)) => Evil(Father(John)) …

29 13/5/2011 TP 2623, shereen@ftsm. ukm. my Universal Instantiation (UI) Rule • Infer any sentence obtained by substituting a ground term for the variable. ▫ Ground term: a term without variables (i. e g). Where Subst(θ, α) is the result of applying the substitution θ to the sentence α for any variable v and ground term g • E. g. The three sentences given earlier: {x/John}, {x/Richard}, and {x/Father(John)}

30 13/5/2011 TP 2623, shereen@ftsm. ukm. my Existential Instantiation (EI) Rule • For any sentence α, variable v, and constant symbol k that does not appear elsewhere in KB, E. g. yields Crown(C 1) On. Head(C 1, John) Provided that C 1 is a new constant symbol, called a Skolem constant. • The existential sentence says that there is some object satisfying a condition, and the instantiation process is just giving a name to the object.

31 13/5/2011 TP 2623, shereen@ftsm. ukm. my Inference rules for quantifiers (Cont’d) • UI can be applied several times to add new sentences; the new KB is logically equivalent to the old. • EI can be applied once to replace the existential sentence; the new KB is not logically equivalent to the old, but is satisfiable iff the old KB is satisfiable, called inferentially equivalent.

32 13/5/2011 TP 2623, shereen@ftsm. ukm. my Reduction to Propositional inference • Suppose the KB contains just the following: King(John) Greedy(John) Brother(Richard, John) • Apply UI to the first sentence using all possible ground term substitution from the vocabulary of the KB, e. g. {x/John} and {x/Richard}: King(John) ^ Greedy(John) => Evil(John) King(Richard) ^ Greedy(Richard) => Evil(Richard) • And discard the universally quantified sentence.

33 13/5/2011 TP 2623, shereen@ftsm. ukm. my Unification • Unification is a process of finding substitutions that make different logical expressions look identical. • UNIFY algorithm takes two sentences and return a unifier for them if one exist: UNIFY(p, q) = θ where SUBST(θ, p) = SUBST(θ, q) • We can get the inference immediately if we can find a substitution θ such that: King(x) and Greedy(x) match King(John) and Greedy(y) θ = {x/John, y/John}

34 Unification (Cont’d) TP 2623, shereen@ftsm. ukm. my 13/5/2011 • E. g. Query: Knows(John, x): Whom does John know? ▫ Answers: Find all sentences in the KB that unify with Knows(John, x). • Results of unification with four diff sentences in KB: p q θ Knows(John, x) Knows(John, Jane) {x/Jane} Knows(John, x) Knows(y, Bill) {x/Bill, y/John} Knows(John, x) Knows(y, Mother(y)) {y/John, x/Mother(John)} Knows(John, x) Knows(x, Elizabeth) fail • Standardizing apart eliminates overlap of variables, e. g. Knows(z 17, Elizabeth)

35 13/5/2011 Generalized Modus Ponens (GMP) TP 2623, shereen@ftsm. ukm. my • First-order inference rule King(John) Greedy(John) • Inference process for John is evil: ▫ Find some x such that x is a king and x is greedy ▫ Infer that this x is evil • If there is some substitution θ that makes the premise of the implication identical to the sentences already in the KB, then assert the conclusion of the implication, after applying θ.

36 GMP (Cont’d) 13/5/2011 TP 2623, shereen@ftsm. ukm. my • More general inference step, where everyone is also greedy: • Conclusion: Evil(John) ▫ John is a king ▫ John is greedy (because everyone is greedy) • For atomic sentences pi, pi’, and q, where there is a substitution θ such that SUBST(θ, pi’) = SUBST(θ, pi), for all i,

37 13/5/2011 GMP (Cont’d) • There are n+1 premises to this rule: ▫ n atomic sentences pi’ ▫ 1 implication • The conclusion is the result of applying the substitution θ to the consequent q. • E. g. : p 1’ is King(John) p 2’ is Greedy(y) θ is {x/John, y/John} SUBST(θ, q) is Evil(John) p 1 is King(x) p 2 is Greedy(x) q is Evil(x) TP 2623, shereen@ftsm. ukm. my

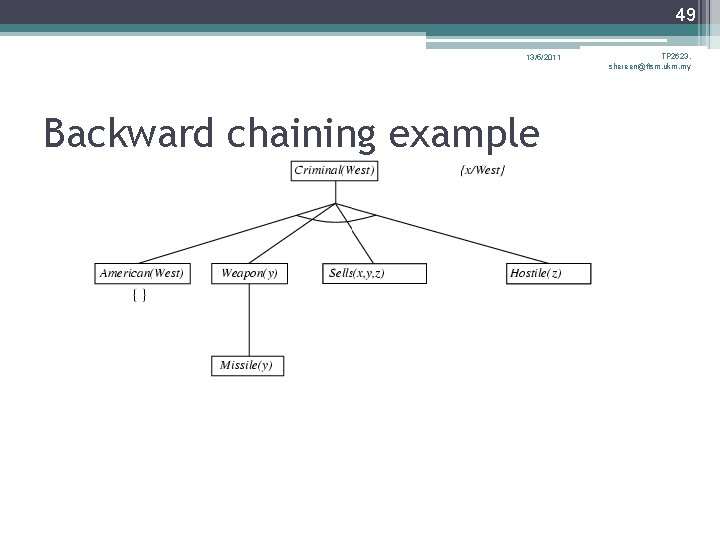
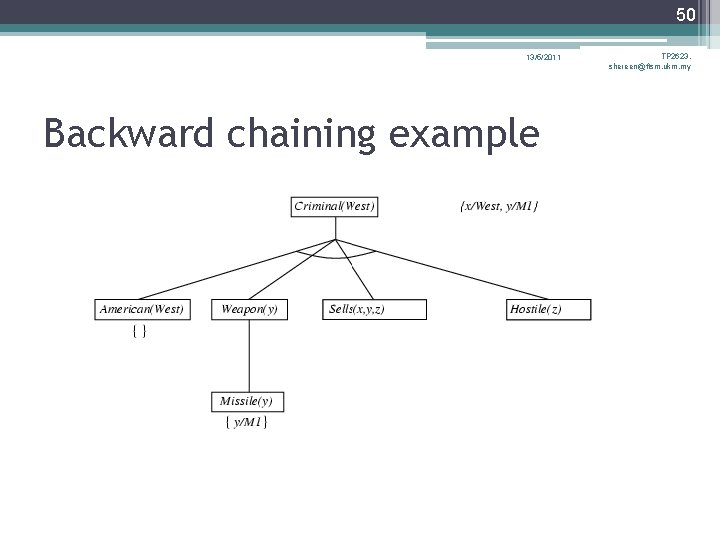
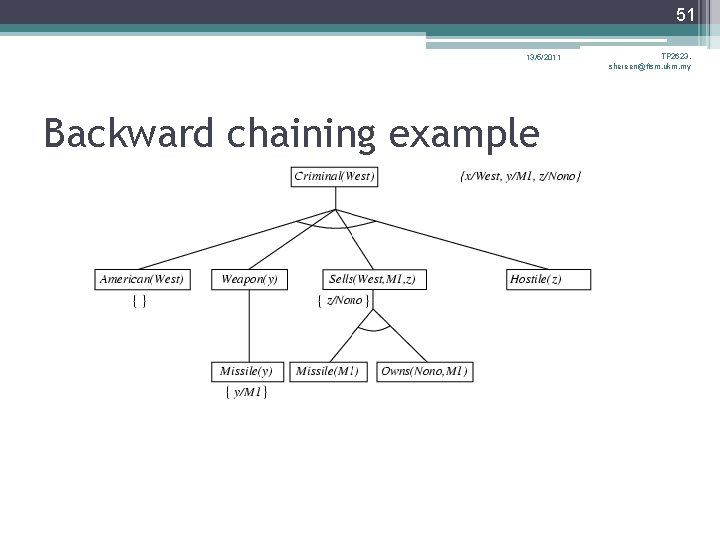
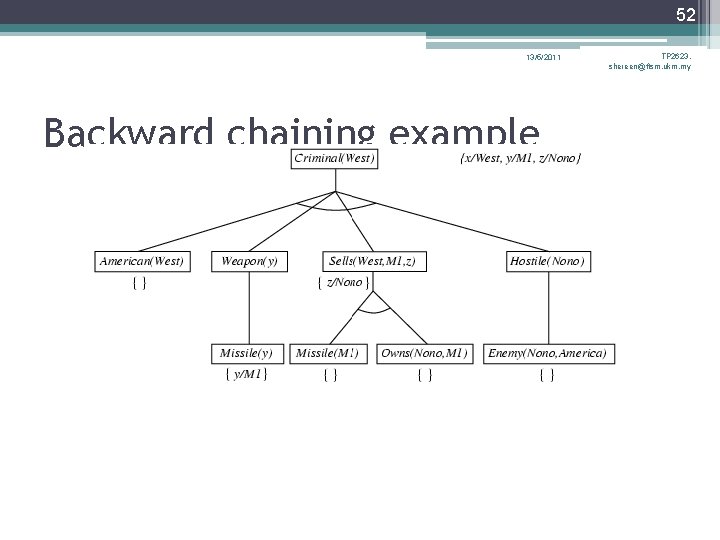
38 13/5/2011 TP 2623, shereen@ftsm. ukm. my Example knowledge base • The law says that it is a crime for an American to sell weapons to hostile nations. The country Nono, an enemy of America, has some missiles, and all of its missiles were sold to it by Colonel West, who is American. • Prove that Col. West is a criminal

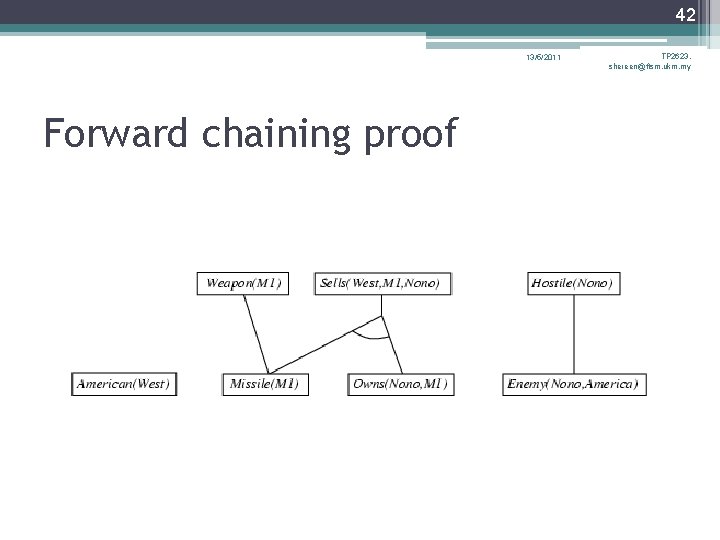
39 13/5/2011 TP 2623, shereen@ftsm. ukm. my Example knowledge base contd. . it is a crime for an American to sell weapons to hostile nations: American(x) Weapon(y) Sells(x, y, z) Hostile(z) Criminal(x) Nono … has some missiles, i. e. , x Owns(Nono, x) Missile(x) Owns(Nono, M 1) Missile(M 1) … all of its missiles were sold to it by Colonel West Missile(x) Owns(Nono, x) Sells(West, x, Nono) Missiles are weapons: Missile(x) Weapon(x) An enemy of America counts as "hostile“: Enemy(x, America) Hostile(x) West, who is American … American(West) The country Nono, an enemy of America … Enemy(Nono, America)

40 TP 2623, samn@ftsm. ukm. my Forward chaining algorithm

41 13/5/2011 Forward chaining proof TP 2623, shereen@ftsm. ukm. my

42 13/5/2011 Forward chaining proof TP 2623, shereen@ftsm. ukm. my

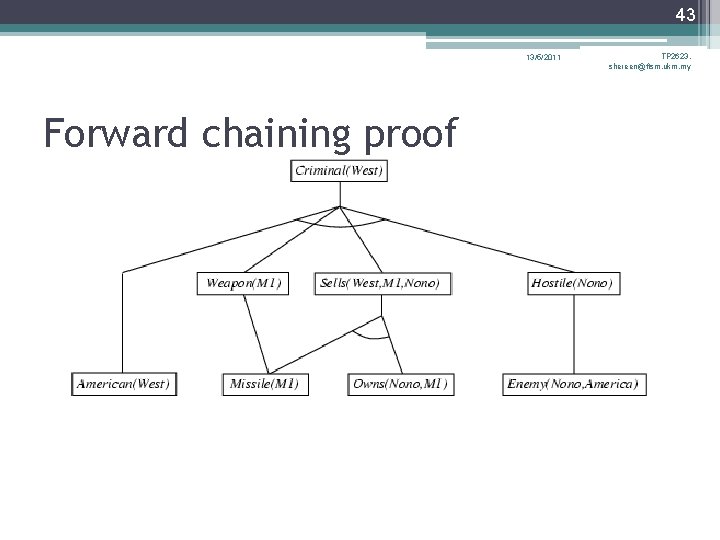
43 13/5/2011 Forward chaining proof TP 2623, shereen@ftsm. ukm. my

44 13/5/2011 TP 2623, shereen@ftsm. ukm. my Properties of forward chaining • Sound and complete for first-order definite clauses • Datalog = first-order definite clauses + no functions • FC terminates for Datalog in finite number of iterations • May not terminate in general if α is not entailed Forward chaining is widely used in deductive databases

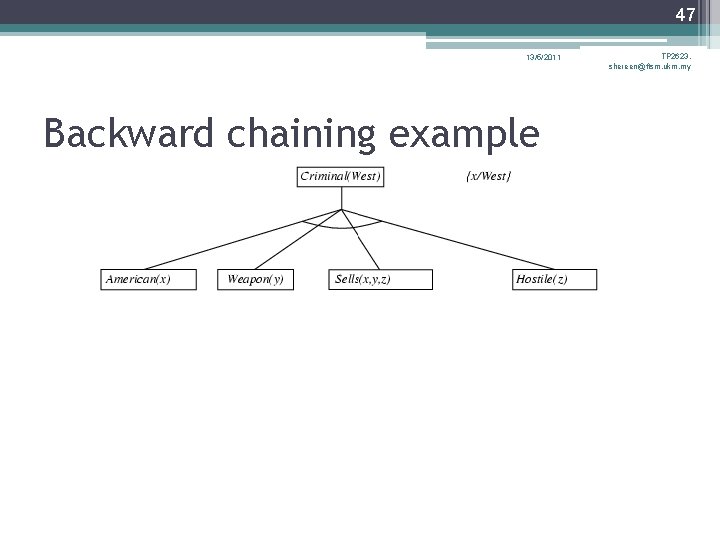
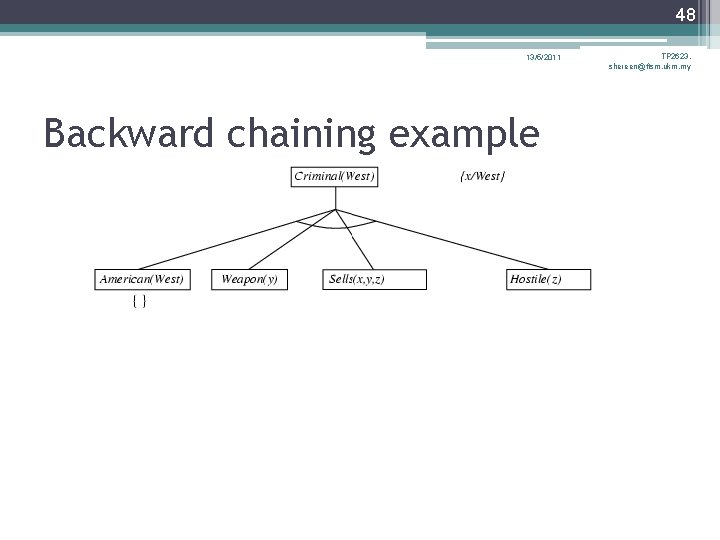
45 13/5/2011 TP 2623, shereen@ftsm. ukm. my Backward chaining algorithm SUBST(COMPOSE(θ 1, θ 2), p) = SUBST(θ 2, SUBST(θ 1, p))

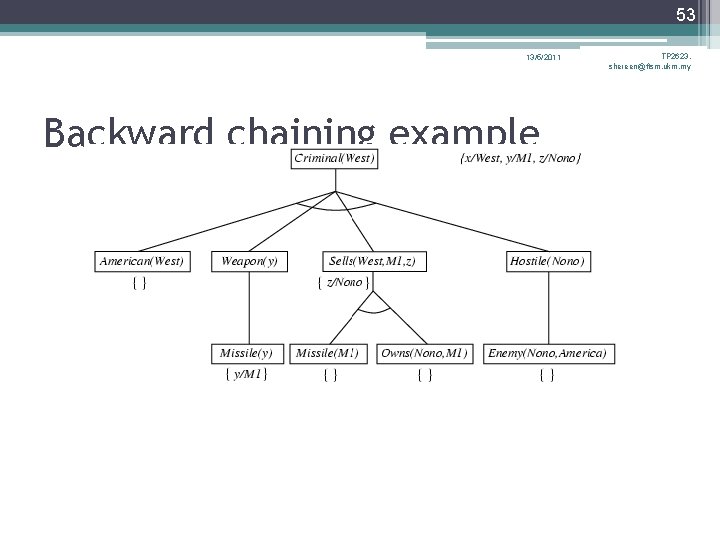
46 13/5/2011 Backward chaining example TP 2623, shereen@ftsm. ukm. my

47 13/5/2011 Backward chaining example TP 2623, shereen@ftsm. ukm. my

48 13/5/2011 Backward chaining example TP 2623, shereen@ftsm. ukm. my

49 13/5/2011 Backward chaining example TP 2623, shereen@ftsm. ukm. my

50 13/5/2011 Backward chaining example TP 2623, shereen@ftsm. ukm. my

51 13/5/2011 Backward chaining example TP 2623, shereen@ftsm. ukm. my

52 13/5/2011 Backward chaining example TP 2623, shereen@ftsm. ukm. my

53 13/5/2011 Backward chaining example TP 2623, shereen@ftsm. ukm. my

54 13/5/2011 TP 2623, shereen@ftsm. ukm. my Properties of backward chaining • Depth-first recursive proof search: space is linear in size of proof • Incomplete due to infinite loops ▫ fix by checking current goal against every goal on stack • Inefficient due to repeated subgoals (both success and failure) ▫ fix using caching of previous results (extra space) • Widely used for logic programming

55 TP 2623, shereen@ftsm. ukm. my End of Topic 5 13/5/2011