Knowledge Representation and Reasoning 2 Advance Artificial Intelligence

Knowledge Representation and Reasoning 2 Advance Artificial Intelligence 1

Knowledge Representation & Reasoning Knowledge representation is the study of how knowledge about the world can be represented and what kinds of reasoning can be done with that knowledge. We will discuss two different systems that are commonly used to represent knowledge in machines and perform algorithmic reasoning: • Propositional calculus • Predicate calculus Advance Artificial Intelligence 2

Predicate Calculus So it is a better idea to use predicates instead of propositions. This leads us to predicate calculus. Predicate calculus has symbols called • object constants, • relation constants, and • function constants These symbols will be used to refer to objects in the world and to propositions about the word. Advance Artificial Intelligence 3

Components Object constants: Strings of alphanumeric characters beginning with either a capital letter or a numeral. Examples: XY, Allahabad, 154, H 1 B Function constants: Strings of alphanumeric characters beginning with a lowercase letter and (sometimes) superscripted by their “arity”: Examples: father. Of 1, distance. Between 2 Advance Artificial Intelligence 4

Components Relation constants: Strings of alphanumeric characters beginning with a capital letter and (sometimes) superscripted by their “arity”: Examples: Beats. Up 2, Tired 1 Other symbols: Propositional connectives , , , and , delimiters (, ), [, ], and separator , . Advance Artificial Intelligence 5

Terms • An object constant is a term. • A function constant of arity n, followed by n terms in parentheses and separated by commas, is a term. Examples: father. Of(Sunita), times(3, minus(5, 2)) Advance Artificial Intelligence 6

Wffs Atoms: • A relation constant of arity n followed by n terms in parentheses and separated by commas is an atom. An atom is a wff. • Examples: Tired(Tanya), Older. Than(Pawan, Afsa) Propositional wffs: • Any expression formed out of predicate-calculus wffs in the same way that the propositional calculus forms wffs out of other wffs is a propositional wff. • Example: Older. Than(Pawan, Afsa) Older. Than(Afsa, Komal) Advance Artificial Intelligence 7

Interpretations An interpretation of an expression in the predicate calculus is an assignment that maps • object constants into objects in the world, • n-ary function constants into n-ary functions, • n-ary relation constants into n-ary relations. These assignments are called the denotations of their corresponding predicate-calculus expressions. Advance Artificial Intelligence 8

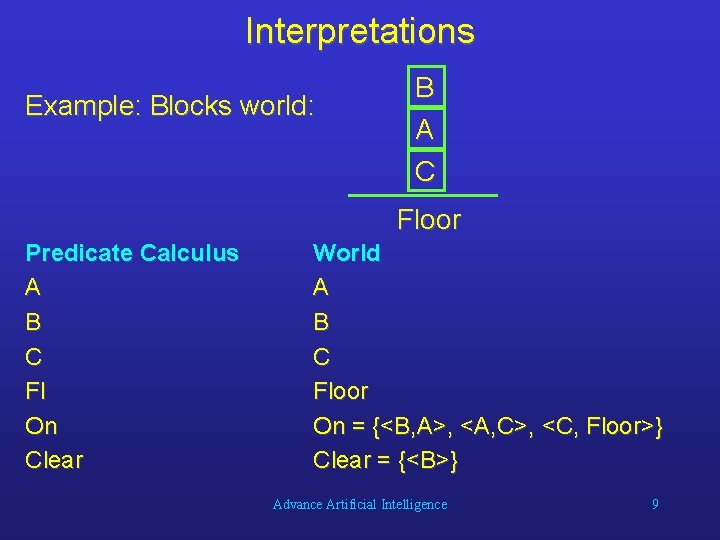
Interpretations Example: Blocks world: B A C Floor Predicate Calculus A B C Fl On Clear World A B C Floor On = {<B, A>, <A, C>, <C, Floor>} Clear = {<B>} Advance Artificial Intelligence 9

Quantification Introducing the universal quantifier and the existential quantifier facilitates the translation of world knowledge into predicate calculus. Examples: Paul beats up all professors who fail him. x(Professor(x) Fails(x, Paul) Beats. Up(Paul, x)) There is at least one intelligent IIITA professor. x(IIITAProf(x) Intelligent(x)) Advance Artificial Intelligence 10

Note about Resolution Refutation You have a set of hypotheses h 1, h 2, …, hn, and a conclusion c. Your argument is that whenever all of the h 1, h 2, …, hn are true, then c is true as well. In other words, whenever all of the h 1, h 2, …, hn are true, then c is false. If and only if the argument is valid, then the conjunction h 1 h 2 … hn c is false, because either (at least) one of the h 1, h 2, …, hn is false, or if they are all true, then c is false. Therefore, if this conjunction resolves to false, we have shown that the argument is valid. Advance Artificial Intelligence 11

Quantification Introducing the universal quantifier and the existential quantifier facilitates the translation of world knowledge into predicate calculus. Examples: Paul beats up all professors who fail him. x(Professor(x) Fails(x, Paul) Beats. Up(Paul, x)) There is at least one intelligent UMB professor. x(UMBProf(x) Intelligent(x)) Advance Artificial Intelligence 12

Knowledge Representation a) There are no crazy UMB students. x (UMBStudent(x) Crazy(x)) b) All computer scientists are either rich or crazy, but not both. x (CS(x) [Rich(x) Crazy(x)] [ Rich(x) Crazy(x)] ) c) All UMB students except one are intelligent. x (UMBStudent(x) Intelligent(x)) x, y (UMBStudent(x) UMBStudent(y) Identical(x, y) Intelligent(x) Intelligent(y)) d) Jerry and Betty have the same friends. x ([Friends(Betty, x) Friends(Jerry, x)] [Friends(Jerry, x) Friends(Betty, x)]) e) No mouse is bigger than an elephant. x, y (Mouse(x) Elephant(y) Bigger. Than(x, y)) Advance Artificial Intelligence 13

Rules of Inference x P(x) _____ P(c) if c U Universal instantiation P(c) for an arbitrary c U __________ x P(x) Universal generalization x P(x) ___________ P(c) for some element c U Existential instantiation P(c) for some element c U __________ x P(x) Existential generalization Advance Artificial Intelligence 14

Rules of Inference Example: Every IS student is a genius. Sonal is a IS student. Therefore, Sonal is a genius. I(x): “x is an IS student. ” G(x): “x is a genius. ” Advance Artificial Intelligence 15

Rules of Inference The steps used can be interpreted as: Step 1: x (I(x) G(x)) Step 2: I(Sonal) G(Sonal) Find some x such that x is an IS student and then infer that x is genius If there is some substitution α that makes the premise of the implication identical to sentences already in the knowledge base , then we can assert the conclusion after applying α. In the above case, {x/Sonal} Advance Artificial Intelligence 16

Unification It is the process of finding substitutions that make different logical expressions look identical. Unify(p, q) = α where Subst(α, p) = Subst(α, q) Advance Artificial Intelligence 17