KNOWLEDGE INSTITUTE OF TECHNOLOGY SALEM Department of Computer

KNOWLEDGE INSTITUTE OF TECHNOLOGY, SALEM Department of Computer Science and Engineering CS 6303 -COMPUTER ARCHITECTURE Mrs. T. Dhivya AP/CSE, KIOT

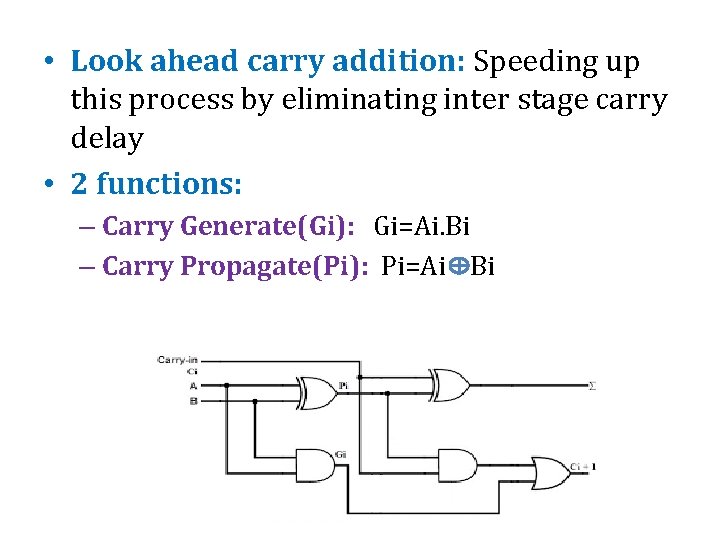
Design of Fast Adder/ Look ahead carry addition • Carry Propagation Delay: The sum and carry outputs of any stage cannot be produces until the input carry occurs; this leads to a time delay in the addition process. • Eg: 0 1 + 0 0 1 1 1 0 0 0

• Look ahead carry addition: Speeding up this process by eliminating inter stage carry delay • 2 functions: – Carry Generate(Gi): Gi=Ai. Bi – Carry Propagate(Pi): Pi=Ai Bi

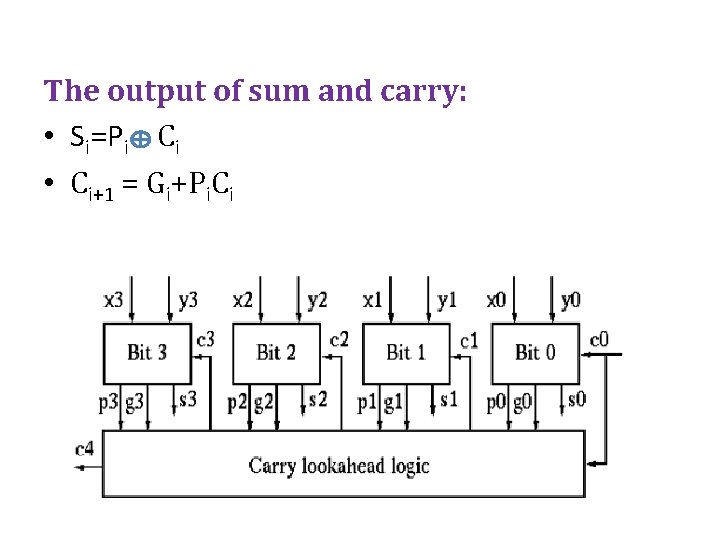
The output of sum and carry: • Si=Pi Ci • Ci+1 = Gi+Pi. Ci

• For example the carriers in a 4 stage carrylookahead adder are defined as follows: • C 1 = G 0+P 0 Cin • C 2 = G 1+P 1 C 1= G 1+P 1 G 0+P 1 P 0 Cin • C 3 = G 2+P 2 C 2= G 2+P 2 G 1+P 2 P 1 G 0+P 2 P 1 P 0 Cin • C 4 = G 3+P 3 C 3= G 3+P 3 G 2+P 3 P 2 G 1+P 3 P 2 P 1 G 0 +P 3 P 2 P 1 P 0 Cin

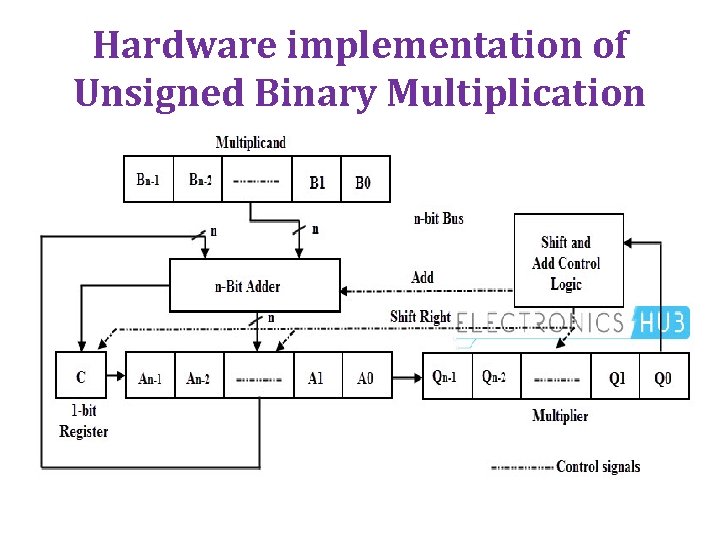
Multiplication • Complex operation than Addition and Subtraction. • It can able to perform in hardware and software • Example: 1 1 0 1 X 1 0 0 1 X 1 1 0 1 (Multiplicand) 1 0 0 1 (Multiplier) 1101 0000 1101 1 0 1 (Final Product) • The Product of 2 n-digit, can accommodated in 2 n digits

Hardware implementation of Unsigned Binary Multiplication

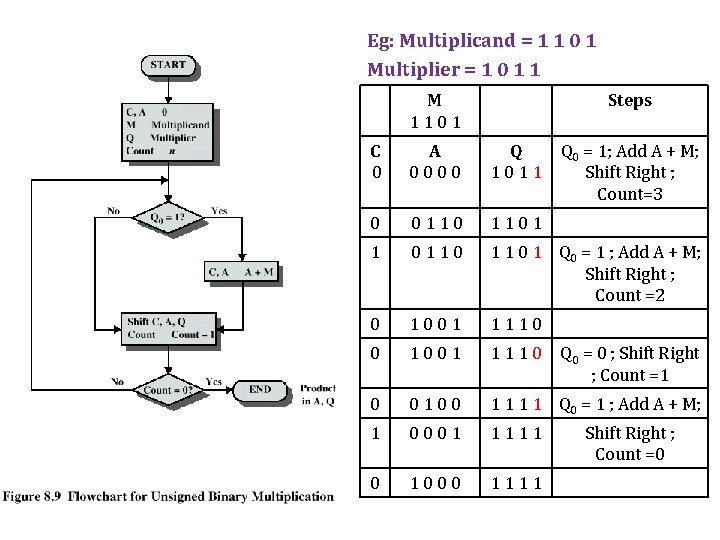
Eg: Multiplicand = 1 1 0 1 Multiplier = 1 0 1 1 M 1101 Steps C 0 A 0000 Q 1011 Q 0 = 1; Add A + M; Shift Right ; Count=3 0 0110 1101 1 0110 1 1 0 1 Q 0 = 1 ; Add A + M; Shift Right ; Count =2 0 1001 1110 0 0100 1 1 Q 0 = 1 ; Add A + M; 1 0001 1111 0 1000 1111 Q 0 = 0 ; Shift Right ; Count =1 Shift Right ; Count =0

Booth’s Algorithm – Signed number multiplication • This algorithm can reduce the number of operations required for multiplication by representing multiplier as a difference between two numbers • Recoding Scheme: A B A-B 0 0 1 -1 1 0 +1 1 1 0 Eg: 1 0 1 1 0 0 for Booth’s algorithm 1 01 1 0 0 -1 +1 0 -1 0 0 0 Implied Zero

Example: Multiplication of signed numbers (-9) x (7) using Booth’s algorithm Step 1: (i) 9 ->1001 1’s complement : 0110 2’s complement: 0110 +1 =10111 7 ->0111 Step 2: Recode the multiplier: 0111 0 -> +1 0 0 -1 Step 3: Multiply 1 0 1 1 1 x +1 0 0 -1 00001001 0000000 10111 110000001

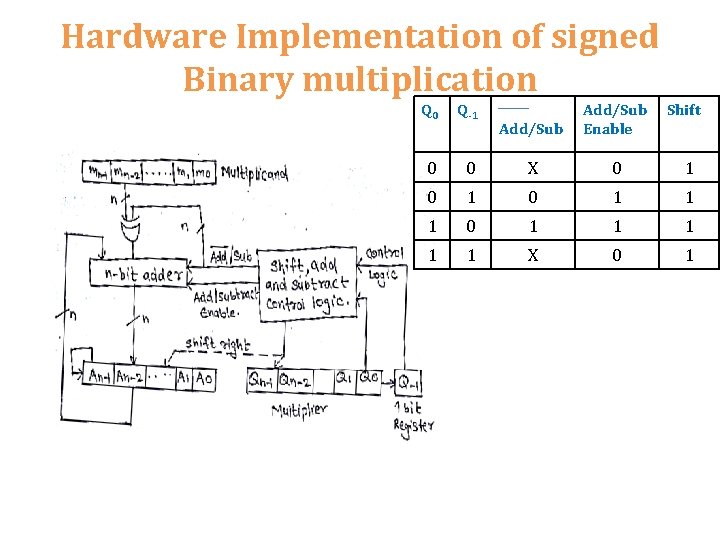
Hardware Implementation of signed Binary multiplication Q 0 Q-1 Add/Sub Enable 0 Shift 0 X 0 1 0 1 1 1 1 1 X 0 1

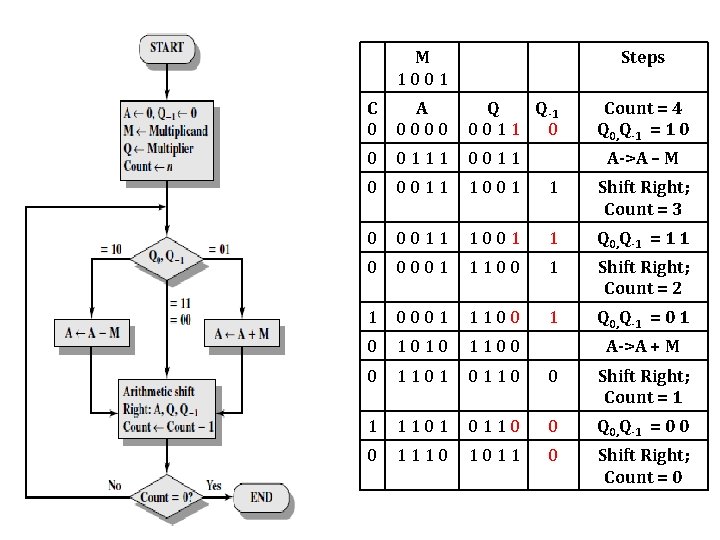
M 1001 Steps C 0 A 0000 Q Q-1 0011 0 Count = 4 Q 0, Q-1 = 1 0 0 0111 0011 0 0011 1001 1 Shift Right; Count = 3 0 0011 1001 1 Q 0, Q-1 = 1 1 0 0001 1100 1 Shift Right; Count = 2 1 0001 1100 1 Q 0, Q-1 = 0 1010 1100 0 1101 0110 0 Shift Right; Count = 1 1 1101 0110 0 Q 0, Q-1 = 0 0 0 1110 1011 0 Shift Right; Count = 0 A->A – M A->A + M

SOLVE? ? • Multiply 10111 x 00111 – Find for Both Signed and unsigned multiplication

Bit Pair Recoding of Multipliers / Modified Booth’s Algorithm • It halves the maximum number of summands. • To speed up the multiplication process in the Booth’s algorithm technique is called as bit pair recoding Multiplier Bit pair recoded bit – pair bit on the right multiplier bit at position i i+1 i i-1 0 0 0 1 +1 0 1 1 +2 1 0 0 -2 1 0 1 -1 1 1 0 -1 1 0

• Example: Find the bit pair for multiplier 11010 Solution: 111010 0 Sign Implied 0 to Right of LSB 0 -1 -2

• Example: Multiply the following pair of signed 2’s complement numbers using bit pair recoding of the multipliers: A=010111 B=101100 • Step 1: Recoded bit pair code for multiplier 1 0 1 1 0 0 0 ->Implied 0 -1 -1 0 • Step 2: Multiplication : 0 1 1 1 x -1 -1 0 00000 11101001 1000 110100

SOLVE? ? ? • Explain Booth’s algorithm to multiply the following pair of signed 2’s complement numbers • A= 110011 multiplicand • B= 101100 multiplier • Also, implement the above using bit – pair recoding and explain how it achieves faster multiplication • Answer: 00100000100

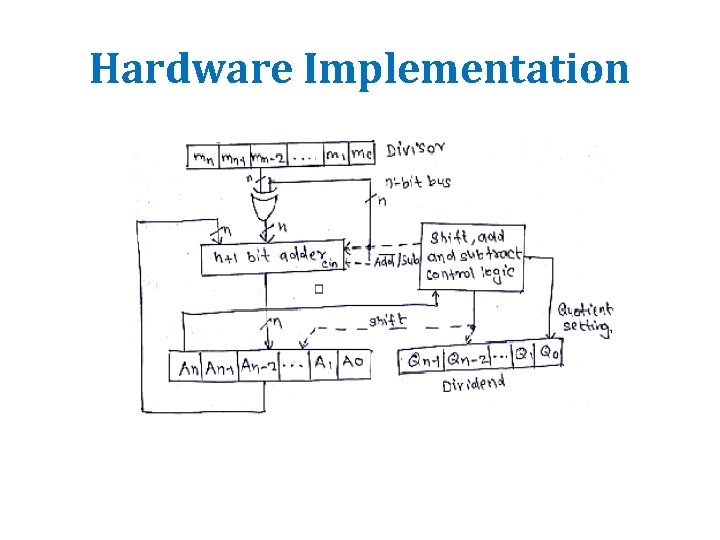
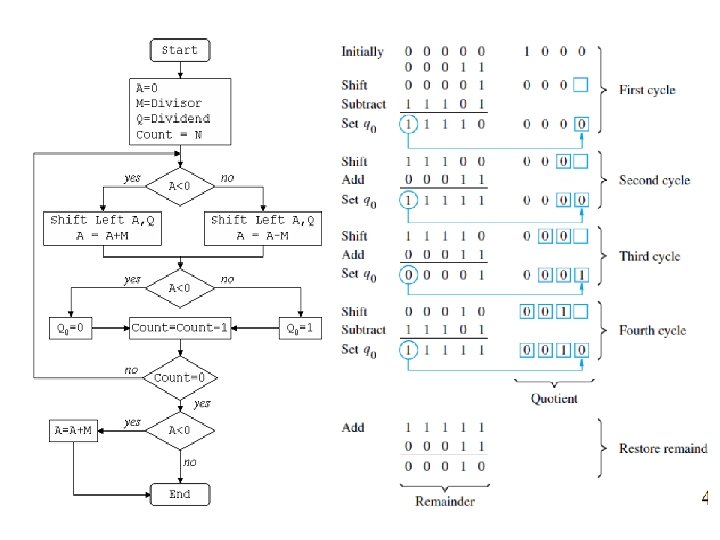
Division • Divide’s two operands, called the dividend and divisor, and the result, called the quotient, are accompanied by a second result, called the remainder. • Eg: Divide 10001010 by 1000 Dividend Divisior-10001010 10001 - Quotient 1000 01010 1000 10 – Remainder

• Relationship between the components: Dividend = Quotient X Divisor +Remainder • Division algorithm can be categorized into 2 ways: – Restoring Division – Non-Restoring Division

Hardware Implementation

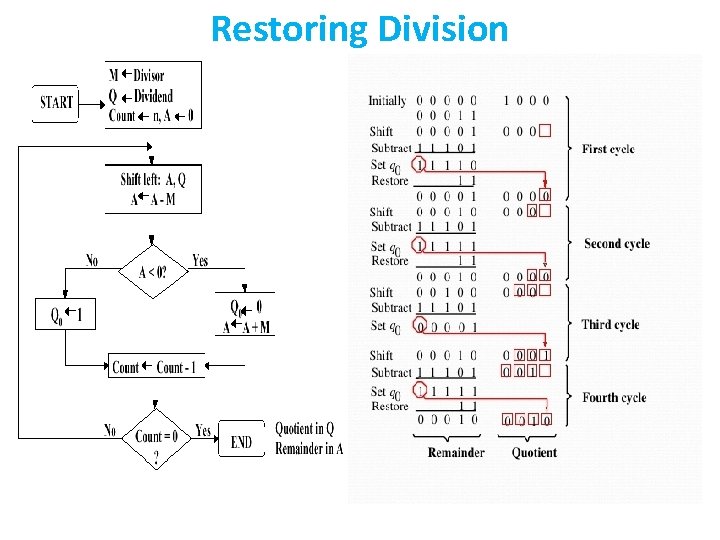
Restoring Division

SOLVE? • Divide 1001101 /1000 – Find both restoring and non restoring method

FLOATING POINT • Floating Point: Going beyond signed and unsigned integers, programming languages support • numbers with fractions, which are called reals in mathematics. Here are some • Examples of reals: – 3. 14159265… ten (pi) – 2. 71828… ten (e) – 0. 00001 ten or 1. 0 ten × 10 -9 (seconds in a nanosecond) – 3, 155, 760, 000 ten or 3. 15576 ten × 109(seconds in a typical century) • In binary, the form is (1. xxxxx) X 2 yyyyyy Eg: 1. 0 X 2 -1

Floating Point Representation • It has 3 fields – Sign – Exponent – Mantissa • Eg: 111101. 1000110 can be represented as: – 1. 111011000110*25 Exponent Mantissa Scaling Factor Therefore, Sign= 1 Mantissa = 111011000110 Exponent = 5

• The two most common floating point storage formats are defined by the IEEE 754 standard and are: • short real: 32 bit (also called single precision) S ( 1 bit )| EXPONENT ( 8 bits ) | MANTISSA ( 23 bits ) • Exponent E, value actually stored in the exponent field is E´=E(Exponent) + Bias(127) • long real: 64 bit (also called double precision) S ( 1 bit )| EXPONENT( 11 bits ) | MANTISSA ( 52 bits ) • Exponent E, value actually stored in the exponent field is E´=E(Exponent) + Bias(1023)

Represent 1259. 12510 in Single Precision and Double Precision Formats Solution: Step 1: Convert decimal value into binary value 1259 =100 1110 1011 0. 125 = 0. 001 Binary number = 100 1110 1011. 001 Step 2: Normalize the number 100 1011. 001 = 1. 00 1110 1011 001 x 210 Step 3: Here S=0 (+ve number) E=10 M=0011101011001

Step 4: Single Precision Bias =127 Therefore E´ = E +127 = 10 + 127 = 137 = 100010012 0 10001001 001110101100100000 Step 5: Double Precision Bia. S=1023 Therefore E´ = E +1023 = 10 + 1023 = 1034 = 100000010012 0 10000001001 0 0 1 1 1 0 0 0 0 0 0 …………. . 0 0 0