Knicole Colon Deepali Dhar Jeff Kaplan Joseph Kowalski






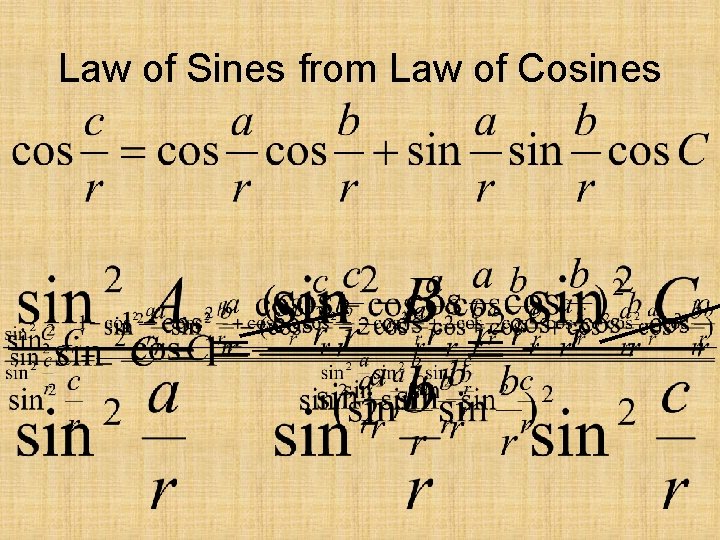

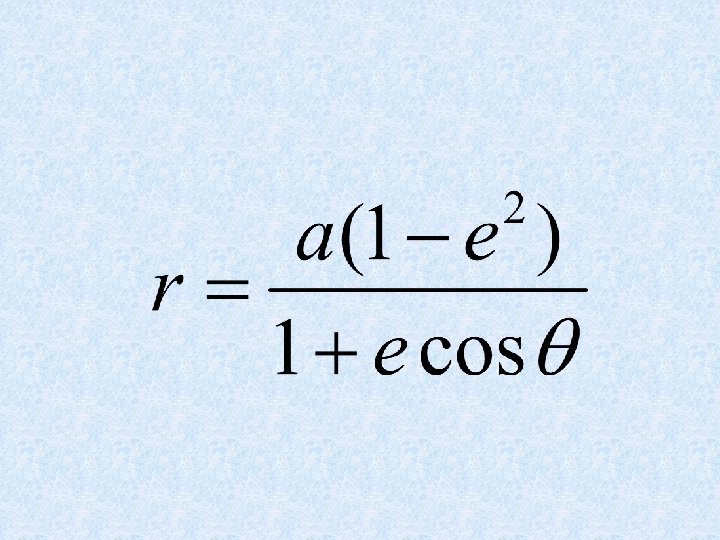



































- Slides: 61

Knicole Colon, Deepali Dhar, Jeff Kaplan Joseph Kowalski, Brandon Levan, D. Martin Ma Parker Meares, Jennifer Mitchel, Tyler Patla, Kirsten Ruch Advisor: Dr. Steve Surace Leader: Sally Warner

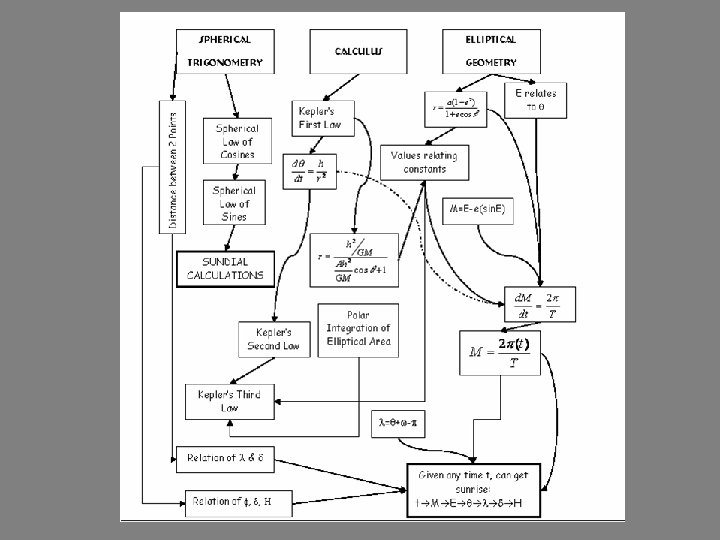
Abstract • What is Celestial Mechanics? Celestial Mechanics is study of the motion of celestial bodies such as stars, the sun, the planets and the moon. • We used derived laws of celestial mechanics to: – find the sunrise on any given day – calculate the latitude of the Arctic Circle – construct a sundial • We used spherical trigonometry to create a “Celestial Sphere” - what we see when we look at the sky.


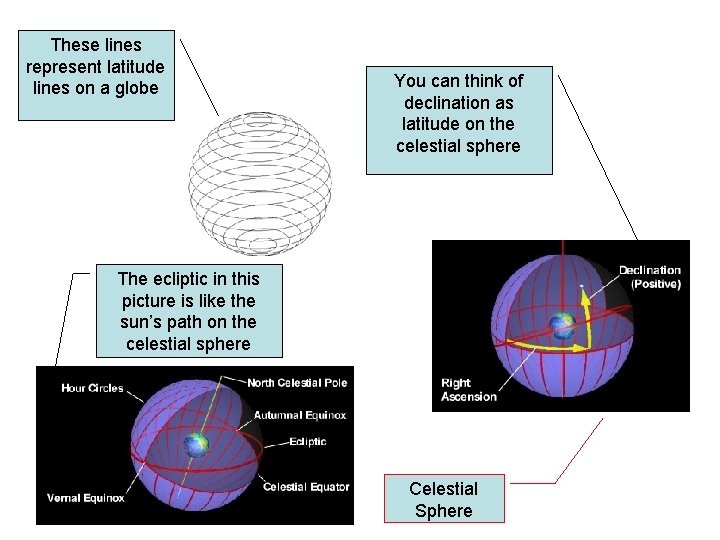
These lines represent latitude lines on a globe You can think of declination as latitude on the celestial sphere The ecliptic in this picture is like the sun’s path on the celestial sphere Celestial Sphere

Spherical Trigonometry Ø What is THIS? - Spherical trigonometry deals with triangles that lie on the surface of a sphere. - The sides of these triangles are created by using arcs of great circles

Spherical Trigonometry Why? - It is the foundation of working with celestial bodies What do we have to do? - We want to makes the laws of 2 D trigonometry, like the Law of Sines and the Law of Cosines, applicable to spheres.

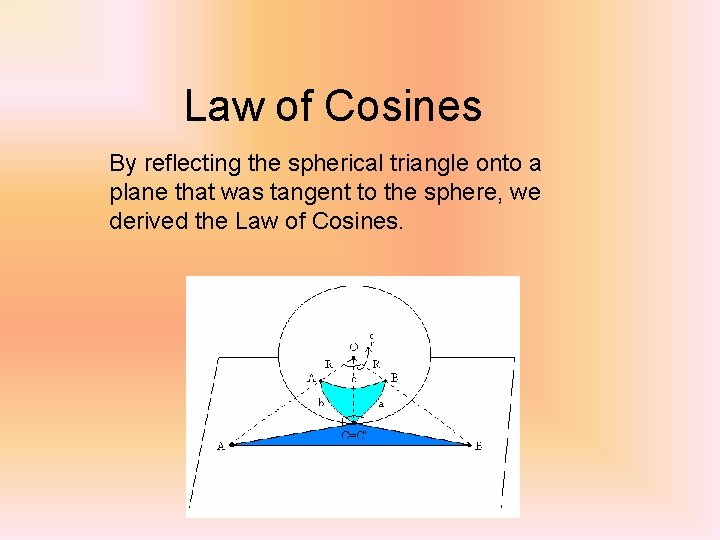
Law of Cosines By reflecting the spherical triangle onto a plane that was tangent to the sphere, we derived the Law of Cosines.

Law of Cosines Finally!!!

Law of Sines From the Law of Cosines, we can derive the Law of Sines by using trigonometric identities and a lot of algebra.
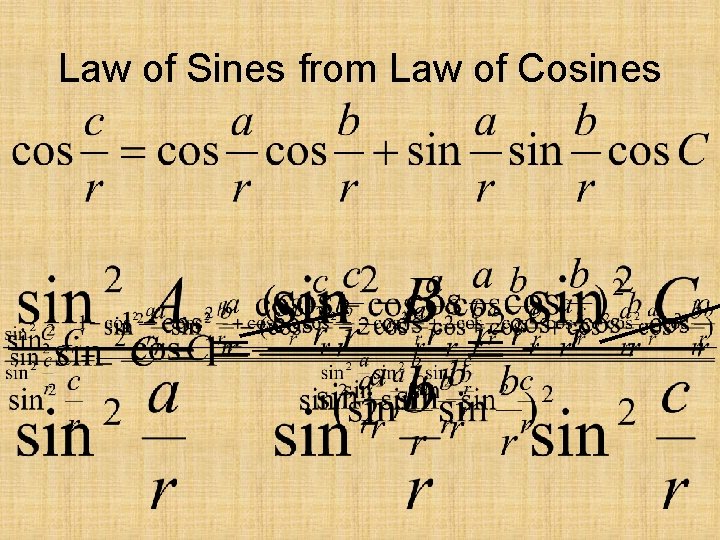
Law of Sines from Law of Cosines

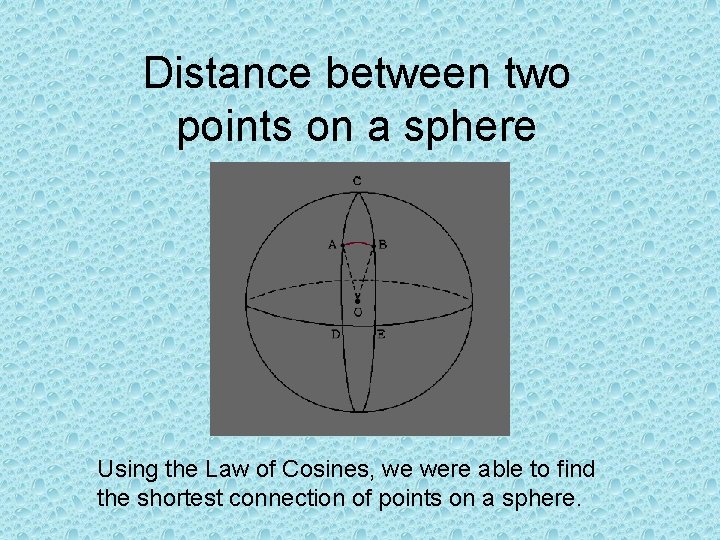
Distance between two points on a sphere Using the Law of Cosines, we were able to find the shortest connection of points on a sphere.

Results of Spherical Trigonometry Ø We rediscovered important and basic laws of trigonometry so that they apply to spheres Ø Now we can apply these laws to help us solve other more important problems

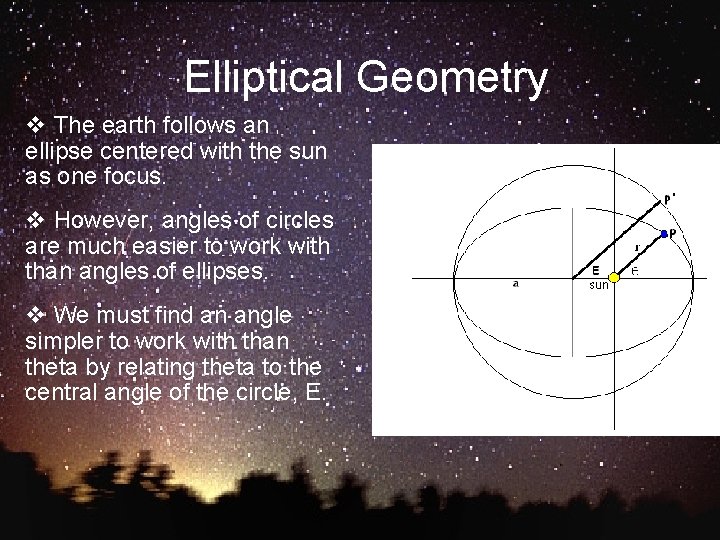
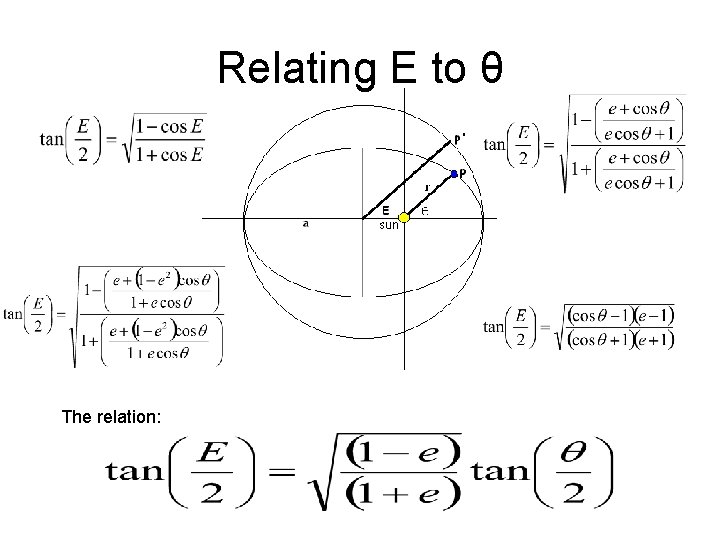
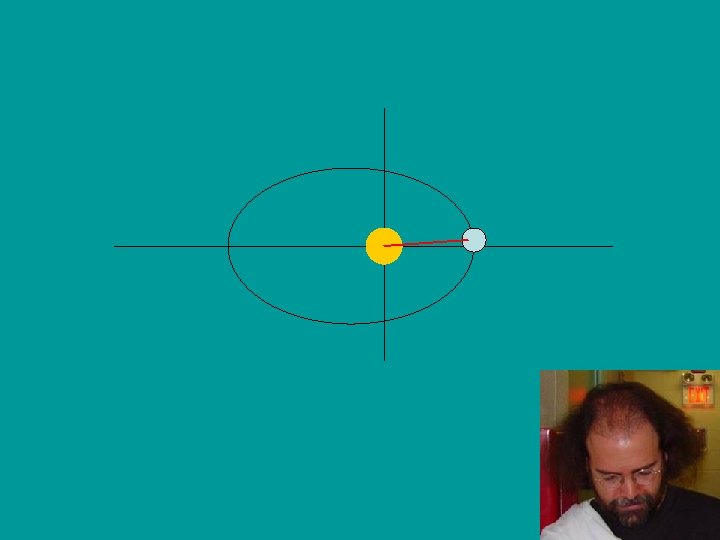
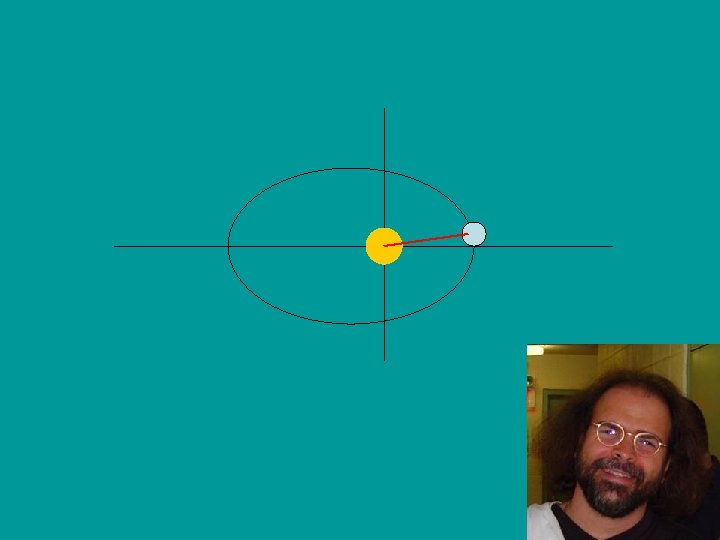
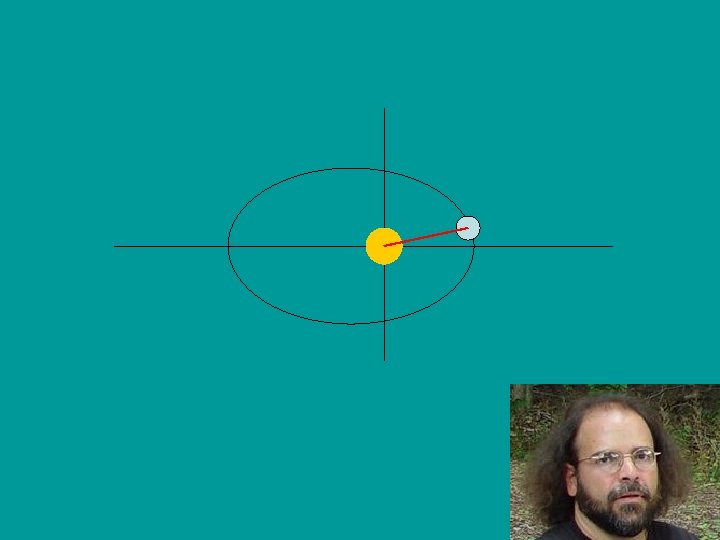
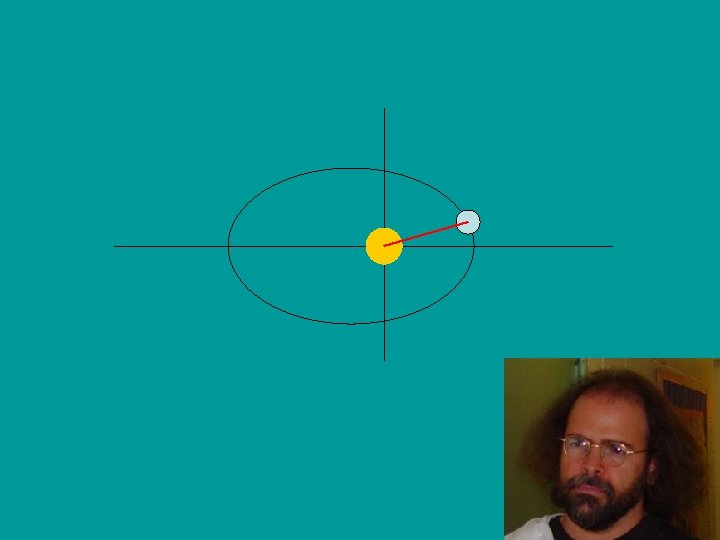
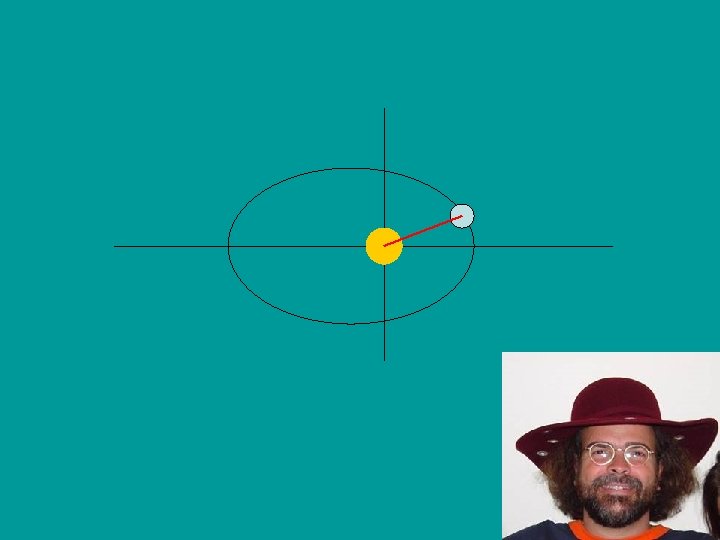
Elliptical Geometry v The earth follows an ellipse centered with the sun as one focus. v However, angles of circles are much easier to work with than angles of ellipses. v We must find an angle simpler to work with than theta by relating theta to the central angle of the circle, E.
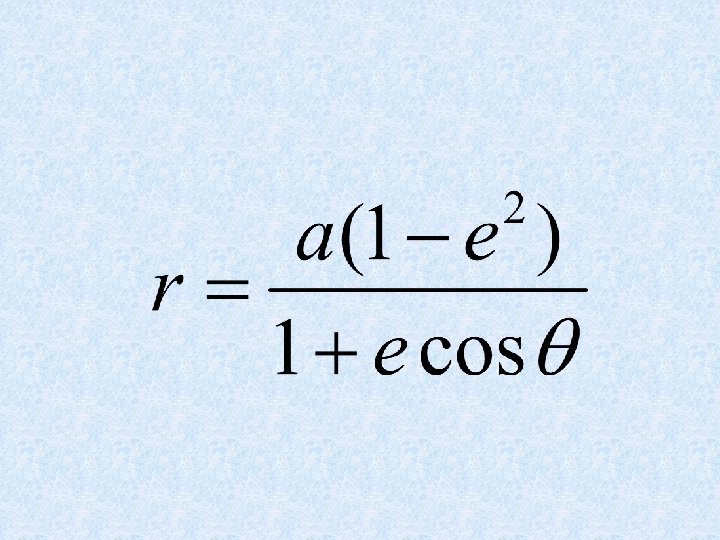

Relating E to θ The relation:

and E, a match made in heaven • This derivation provides us with a direct relation between our and the central angle E. • This relationship will be combined with Kepler’s Laws.

Kepler’s First Law • Planets move in elliptical orbits, with the sun at one of the foci of the ellipse, whereas it was previously thought that the planets orbited in circular paths. Earth travels in an elliptical orbit Focus of Ellipse Sun at other focus of ellipse

Kepler’s First Law • We derived the gravitational force on a planet from both the x and y directions.

Kepler’s First Law • After great simplification, we can determine that the radius of the earth’s orbit is a function of the angle from perihelion.

Kepler’s First Law • Comparing this equation with the geometric equation for an ellipse with the sun at a focus, we find out they are the same and can relate certain values to each other.

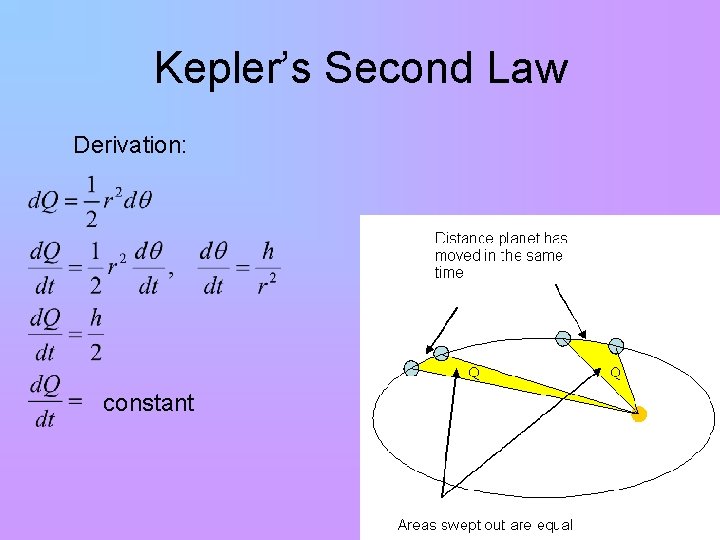
Kepler’s Second Law Derivation: constant

Kepler’s Second Law • The area of the sector of the ellipse over one change in time is equal to the same change in time over any other part of the orbit. • Planets move faster when they are closer to the sun, covering a greater area. They move slower when farther from the sun, as the centripetal gravitational force is smaller.

Kepler’s Third Law • The equations for the area of an ellipse can help us relate the time period to length a

Kepler’s Third Law • Using that equation, we can prove that the square of the period (T²) is proportional to the cube of the semi-major axis (a³)

Kepler’s Laws • Kepler figured his laws out by observation. Only later could they be derived mathematically from Newton’s laws. • We continue to use these fundamentals of elliptical orbits and equal area movement to derive other equations and statistics about our universe and our view of it.

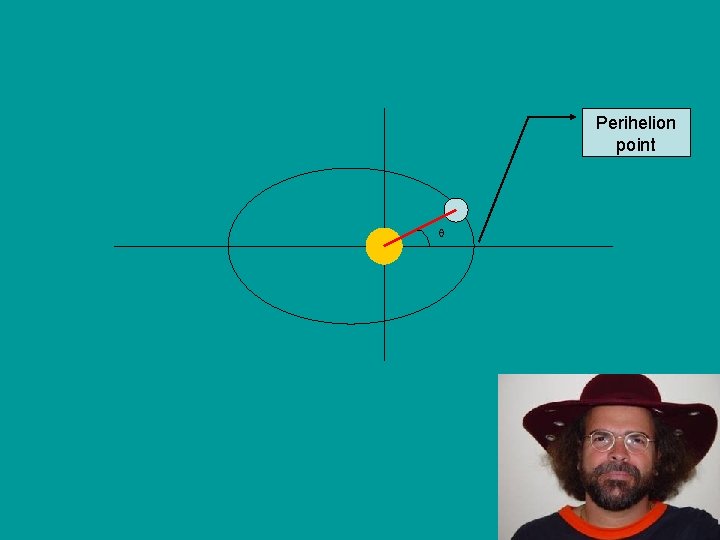
Tracking angle • The equation we have has angle , but what does this represent? • Take a look at the following diagram, the earth starts at the perihelion point, (which is around January 3) • is the angle from the x-axis to the line connecting the earth and the sun







Perihelion point

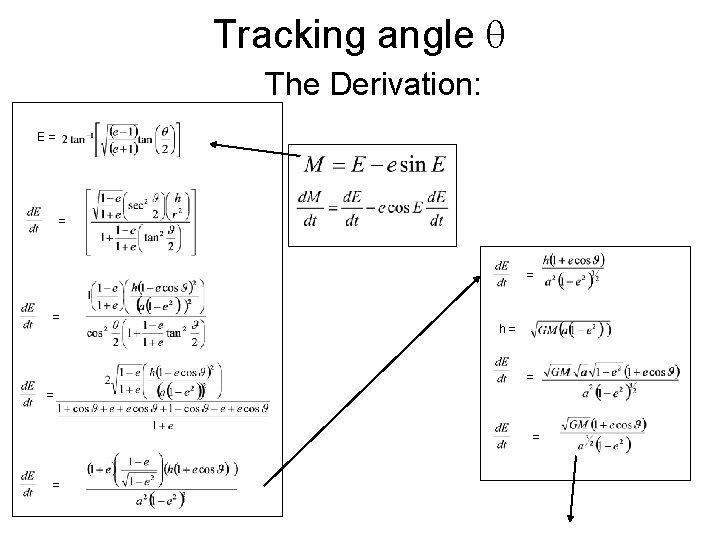
Tracking angle • does not change at a constant rate. • We need some quantity (M) that changes at a constant rate because each day goes by at a constant rate (24 hours per day).

Tracking angle The Derivation: E= = h= = =

More of the Derivation

Tracking angle • Now we have related to the time in this sequence: t M E • This essentially gives us the motion of the planets as a function of time

Finding • θ measures the angle from January 3, but measures from March 21, the vernal equinox • March 21 is a reference point since it has a 12 hour day – the first day of spring

Declination • Declination is a measure of the deviation of the sun from a straight path along the earth’s equator • Higher declination = longer day

Derivation of Declination • We know the maximum declination, , is 23. 43975. • Using the law of sines: Using this, we can find the declination on any day.

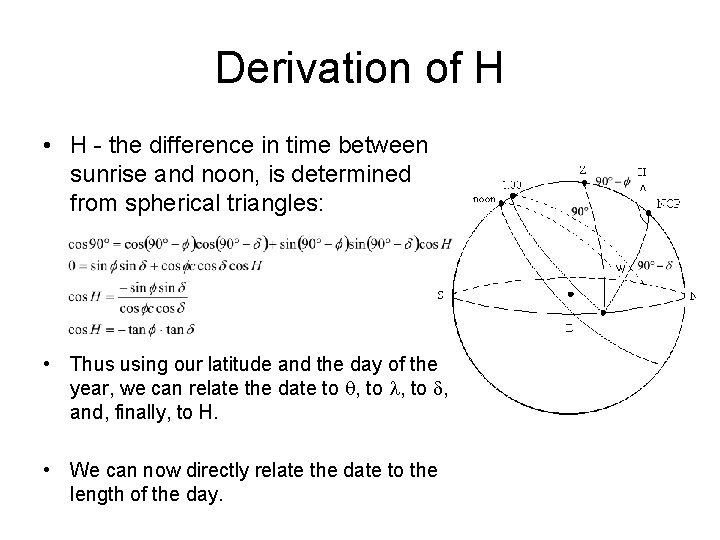
H: The path of the sun in the sky • The length of the day depends on declination and our latitude, 41 • H is the time from sunrise to noon and from noon to sunset

Derivation of H • H - the difference in time between sunrise and noon, is determined from spherical triangles: • Thus using our latitude and the day of the year, we can relate the date to , and, finally, to H. • We can now directly relate the date to the length of the day.

Results of Knowing H • H is the final variable in the series that now enables us to convert the date into the length of the day t M E H

Calculating the Sunrise • By now we have all information describing the apparent motion of the sun, and tracking its path in the sky • Using this information, we can calculate the sunrise at any given day

Calculating the Sunrise • Using today, Friday August 16 2002, as the day, we set t = 228 days, since August 16 is 228 days from January 3 rd.

Calculating the Sunrise • A time of 6. 7566 hours between midday and sunrise yields a sunrise time of 6: 15 A. M. • When compared to 3 researched values (6: 09, and 6: 07), this time is accurate within 8 minutes or 0. 56%.

Finding the Arctic Circle • Ever wondered how far north you have to go before you reach somewhere the sun never sets? • Well, that is what we have calculated: the latitude of the Arctic and Antarctic Circles

Calculating the Arctic Circle • The latitude where the sunrise is 12 hours from noon on the summer solstice is the latitude of the Arctic Circle. • Also, on the summer solstice, the declination of the sun is at its maximum, which simplifies the calculation

Calculating the Arctic Circle • This latitude of 66. 5603 is equal to a latitude 66 33’, which is the latitude of the Arctic Circle.


Thinking in terms of 3 -dimensional space, several things had to be determined • Latitude ( ) here: 41 • Coordinates of the sun • Coordinates of stick tip pointing north, tilted at • How to track sun’s shadow To do this, the points were first visualized a plane tilted at angle .

Let N be sun’s position in the tilted plane ( degrees) and T be the stick tip. N =(R cos , R sin , 0) T = (0, 0, L) However, since the sundial would be built on a flat surface, the plane had to reflect this. To do this, we rotated the Z and X axis (90 - ). Now: Z’ = to the ground and. . X’= points toward the horizon Y =Y’. .

…doesn’t mean they aren’t out to get me!!!

With the plane tilted, we then recalculated the sun and stick tip positions and fitted a 3 D line to them. z’ = sin( + ) = z cos + x sin NOTE: Y = Y’ (no change in y-axis position) THE NEW POINTS N' = (R cos sin , R sin , R cos ) T' = (-L cos , 0, L sin ) Line Equation

To isolate ‘t’, we used our knowledge that Z’ = 0 where the shadow hits the ground. 0 = L sin + (R cos - L sin )t t was then substituted into the x and y equations to allow us to track the shadow’s progress relative to the center line.

The need now was for a way to calculate the angle between the sun’s shadow and the center line. A tangent expression was formed to do so. … messy algebra … “Abracadabra, alacazam!

Using the tangent expression, these angles were obtained: ANGLE OF ANGLE ON TIME SUN ( º ) X' (cm) GROUND ( º ) 7: 00 AM 90 undefined 90 8: 00 AM 75 247. 5 68 9: 00 AM 60 115 49 10: 00 AM 45 64. 9 33 11: 00 AM 30 38. 4 21 12: 00 PM 15 17. 6 10 1: 00 PM 0 0 0 2: 00 PM -15 17. 6 -10 3: 00 PM -30 38. 4 -21 4: 00 PM -45 64. 9 -33 5: 00 PM -60 115 -49 6: 00 PM -75 247. 5 -68 7: 00 PM -90 undefined -90 All that remained was to set the stick at 41* which again was done with simple trig. (SEE PICTURE)


Conclusion • Using Newton’s Laws and calculus we were able to mathematically prove Kepler’s Laws. • Kepler’s Laws, along with geometry, enable us to predict the motion of the planets using precise mathematical equations rather than relying on past data.

Conclusion • We are able to relate the date to , , , and H, which directly leads to the length of the day, as well as sunrise and sunset. • Our equations also enable us to determine at what latitudes the sun will not set or rise on certain days.

“Yes he is” “No he isn’t” “Yes he is” “Shut up, Surace” “No, you shut up, Surace” The End Why is Brandon staring at me? Hey, he’s cute!
 Knicole colón
Knicole colón What is colon used for
What is colon used for Semicolon example of use
Semicolon example of use Uses of semicolon
Uses of semicolon What is semicolon
What is semicolon Semi-colon vs colon
Semi-colon vs colon Colons examples
Colons examples When is colon used
When is colon used @rip2
@rip2 Vasant dhar
Vasant dhar Ameet dhar
Ameet dhar Epidemais croisiere
Epidemais croisiere Data privacy
Data privacy Piotr kowalski warszawa
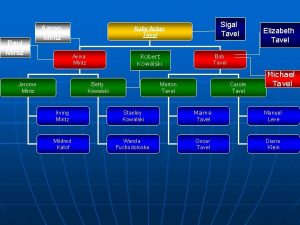
Piotr kowalski warszawa Prolog family tree
Prolog family tree Betty kowalski
Betty kowalski Cindy kowalski
Cindy kowalski Włodzimierz kowalski
Włodzimierz kowalski Pawel kowalski
Pawel kowalski Zachariasz kowalski
Zachariasz kowalski Constella fass
Constella fass Kaplan's icons
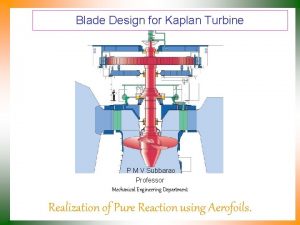
Kaplan's icons Kaplan turbine formula
Kaplan turbine formula Dina c. kaplan
Dina c. kaplan Rotor francis
Rotor francis Kaplan and norton strategy map
Kaplan and norton strategy map Kaplan register book
Kaplan register book Kaplan blade
Kaplan blade Turbina semi kaplan
Turbina semi kaplan Robert s kaplan balanced scorecard
Robert s kaplan balanced scorecard Soft heaps of kaplan and zwick uses
Soft heaps of kaplan and zwick uses Ba 523
Ba 523 Kaplan meier jmp
Kaplan meier jmp Haim kaplan
Haim kaplan Mudr. vlastislav kaplan
Mudr. vlastislav kaplan Strategic map template
Strategic map template Soren kaplan
Soren kaplan Dnxc bsc
Dnxc bsc Habits of a scholar
Habits of a scholar Turbina kaplan partes
Turbina kaplan partes Los grandes síndromes geriátricos kaplan pdf
Los grandes síndromes geriátricos kaplan pdf Haim kaplan
Haim kaplan Shirish gadgeel
Shirish gadgeel Shay mozes
Shay mozes Frederic kaplan
Frederic kaplan Bailey kaplan
Bailey kaplan Mark kaplan coral glades
Mark kaplan coral glades Chapter 3 skeletal system answer key
Chapter 3 skeletal system answer key Kaplan approach elbow
Kaplan approach elbow Kaplan gre
Kaplan gre Haim kaplan
Haim kaplan Nabrali smo kiticu najljepšega cvijeća tekst
Nabrali smo kiticu najljepšega cvijeća tekst Kaplanlearn
Kaplanlearn Bracketing in counselling
Bracketing in counselling Turbina kaplan componentes
Turbina kaplan componentes Audrey kaplan
Audrey kaplan Feele lab
Feele lab Gülay büyükaksoy kaplan
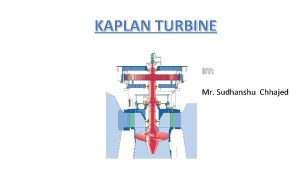
Gülay büyükaksoy kaplan Kaplan turbine
Kaplan turbine Kaplan acca course fee
Kaplan acca course fee Depth and complexity icons meanings
Depth and complexity icons meanings Tesco balanced scorecard
Tesco balanced scorecard