KNAPSACK Algorithms 1 FINITE 2 DEFINITENESS 3 INPUTOUTPUT

KNAPSACK公開金鑰密碼學 Algorithms 1. FINITE 2. DEFINITENESS 3. INPUT/OUTPUT 4. GENERALITY 5. EFFECTIVENESS 1

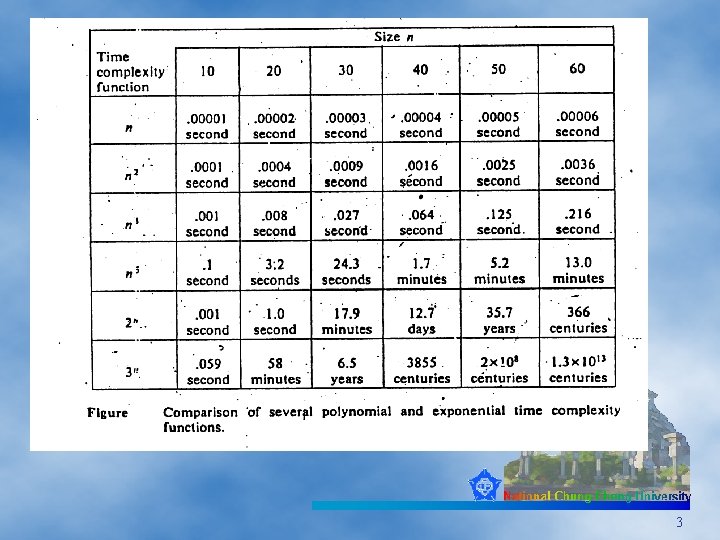
NP-Complete 問題 • 到目前為止尚未有好的Algorithm， 可在Polynomial time解決。 • 如 0/1 -Knapsack 2

3

4

an 5

6

Simple Knapsack Problem • 為一特例，其問題之解可以在Linear time求得 • 向量A 內之元素呈Supper increasing，即 Example N=5，C=14，及A =(1，3，5，10，22) 則 m 5=0 ----因 14<22 m 4=1 ----因 14>10 m 3=0 ----因 4<5 m 2=1 ----因 4>3 m 1=1 ----因 1=1 M=(1, 1, 0) 8

Merkle-Hellman Knapsack 將Simple Knapsack 轉成一般的0/1 Knapsack 1. 選一個Simple Knapsack A =(a 1, a 2, …, an) 2. 選一整數u，使得 u > 3. 選一整數e為加密金鑰，e和u互質 4. 計算解密金鑰d，e × d=1 mod u 5. 轉換A 為一般的0/1 Knapsack A 6. A=(e × A ) mod u 7. Public Key = A 8. Trapdoor = d 和u (A =d. A mod u) 9. 密文C = M× AT 9

Merkle-Hellman Knapsack方法（續） • 解密步驟 轉換密文C為可用Simple Knapsack求解之值C C =d × C mod u =d×MAT mod u =d×M×(e×A T) mod u =MA T 因A 為Simple Knapsack，故M可以很快求得。 10

Example: Merkle-Hellman Knapsack 設A =(1, 3, 5, 10)，u=20和e=7， 則d=3 A=(7, 1, 15, 10) 設M＝ 13，以二進位法表示(1, 1, 0, 1) C=M×AT=7+1+10=18 解密 C =3× 18 mod 20=14 11

Merkle-Hellman Knapsack方法的保密性 • 原先建議n=100，但Knapsack Problem可在T＝ 0 (2 n/2) 時間解決，n=100，250=1015 • 使用一個processor約11574天可完成，1000個處理機 可在 12天完成，故為安全起見，取n=200 • Merkle-Hellman 建議使用多組e，d來重覆處A=e. A 。 • 雖然 0/1 Knapsack 是NP-complete，但不意味著由 Simple Knapsack轉換之Problem一定是NP-complete 12

Example: Graham-Shamir Knapsacks 設n=5，A 如下所示 j Rj Ij Sj 1 011010 10000 000101 =a 1 2 001001 01000 000011 =a 2 3 0100100 000100 =a 3 4 011000 000111 =a 4 5 000110 00001 000001 =a 5 M=(0, 1, 0, 0, 1) C`=M×A T=a 2 +a 5 =(R 2+R 5, I 2+I 5, S 2+S 5)=001111 01001 000100 恰為明文 14

數位簽章 ‧RSA Digital Signature (R. L. Rivest, A. Shamir, and L. M. Adleman, 1978) ‧El. Gamal Digital Signature (T. El. Gamal, 1985) ‧Schnorr’s Digital Signature (C. P. Schnorr, 1989) ‧Blind Signature (D. Chaum, 1983) 15

Introduction q Three Basic Services of Cryptography 1. Secrecy (provided by cryptosystems) 2. Authenticity (provided by digital signature scheme) 3. Integrity (provided by digital signature scheme) q Two Famous Digital Signature Schemes 1. RSA Digital signature scheme (based on the factorization problem) 2. El. Gamal digital signature scheme (based on the discrete logarithm) 16

Introduction q Applications: Blind signature (for electronic commerce) 17

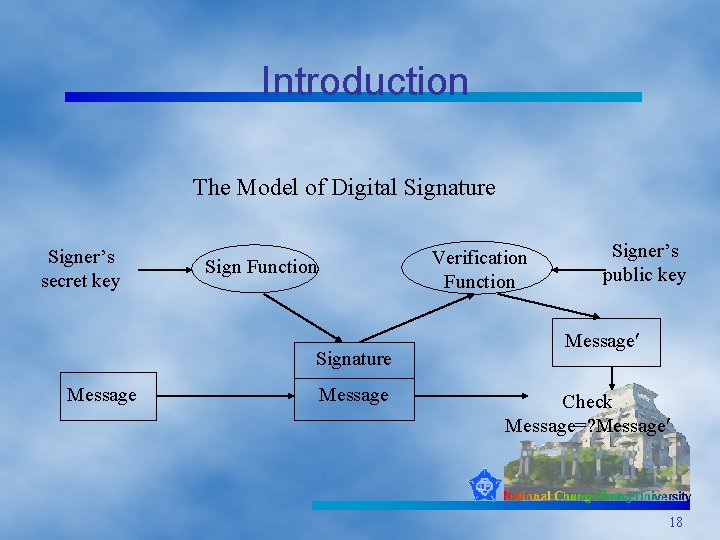
Introduction The Model of Digital Signature Signer’s secret key Verification Function Signature Message Signer’s public key Message Check Message=? Message 18

RSA Public Key Cryptosystem and Digital Signature Scheme q Rivest, Shamir, and Adleman proposed in 1978 q RSA Public Key Cryptosystem ◆ Security Basis: Factorization Problem. ◆ Construction: 1. Choose two large prime numbers P and Q, then compute N=P×Q. 2. Select an integer e such that gcd(e, (N))=1. 3. Compute d such that e×d mod (N)=1. 4. Public key = (N, e). 5. Private key = (P, Q, d). 19

RSA Public Key Cryptosystem and Digital Signature Scheme q RSA Digital Signature Scheme v Sign Function: Signature S=Md mod N. v Verification Function: M=Se mod N. q Example 1. P=11, Q=13, N=143, and (143)=120. 2. e=103, then d=7 (for 103× 7 mod 120=1 ). 3. Sign for M=3: S=37 mod 143=42. 4. Verification: M= Se mod N = 42103 mod 143=3. 20

El. Gamal Public Key Cryptosystem and Digital Signature Scheme q El. Gamal proposed in 1985 q El. Gamal Public Key Cryptosystem ◆ Security Basis: Discrete Logarithm Problem 1. If P is a large prime and g and y are integers, find x such that y=gx mod P. 2. The security restriction on P: P-1 must contain a large prime factor Q. ◆ Construction: 1. Choose a large prime number P and a generator g of GF(P). 2. Private key: a random integer x between 1 and P-1. 3. Public key: y=gx mod P. 21

El. Gamal Public Key Cryptosystem and Digital Signature Scheme q El. Gamal Digital Signature Scheme v Sign Function: Signature (r, s) for message M. 1. Select a random integer k between 1 and P-1 such that gcd(k, P-1)=1. 2. Compute r=gk mod P. 3. Compute s=k-1(M-xr) mod (P-1). v. Verification Function: 1. Verify by checking whether g. M mod P = (rs) ×(yr) mod P. 2. (rs) ×(yr)=g(M-xr) × gxr = g(M-xr)+xr=g. M mod P. 22

El. Gamal Public Key Cryptosystem and Digital Signature Scheme q Example 1. P=23, g=5. 2. x=3, then y=10 (for 53 mod 23=10 ). 3. Sign for the message M=8. 4. Select k=5 between 1 and 22 (P-1). 5. Compute r = gk mod P = 55 mod 23 = 20. 6. Compute s = k-1(M-xr) mod (P-1) = 5 -1(8 -3× 20) mod 22 = 9× 14 mod 22 = 16. 7. Verification: 8. g. M= 58 mod 23 =16 9. (rs)(yr) mod P = 2016 × 1020 mod 23= 13× 3 mod 23 = 16. 23

Schnorr’s Digital Signature Scheme q Schnorr’s Digital Signature Scheme v Sign Function: Signature (r, s) for message M. 1. Select a random integer k between 1 and P-1. 2. Compute r = h(M, gk mod P). 3. Compute s = k + x*r mod (P-1). , where the secret key x the public key y= g-x mod P 4. Send (M, r, s) to the receiver. v. Verification Function: 1. Compute gk mod P=gsyr mod P. 2. Verify by checking whether r = h(M, gk mod P). 24

Blind Signature q D. Chaum proposed in 1983 q D. Chaum’s Blind Signature Scheme ◆ It uses the RSA algorithm. Security Basis: Factorization Problem ◆ Construction: Bob has a public key, e, a private key, d, and a public modulus, N. Alice wants Bob to sign message M blindly. 1. Alice chooses a random integer k between 1 and N. Then she blinds M by computing t = Mke mod N. 2. Bob signs t, td=(Mke)d mod N. 3. Alice unblinds td by computing s=td/k mod N = Md mod N. s is the signature of message M. 25

Blind Signature Property: Untraceable Applications: Blind signature can be used in electronic cash system. Bank 1. t=SN×ke mod N SN: Serial # k: random number 2. t Consumer 4. s=(td)/k mod N=SNd mod N Coin: SN＋s 3. td mod N 5. Coin -signs coins -database 7. Coin Merchant 6. Verify the signature s 26