KLMH VLSI Physical Design From Graph Partitioning to

© KLMH VLSI Physical Design: From Graph Partitioning to Timing Closure Chapter 7 – Specialized Routing Original Authors: Andrew B. Kahng, Jens Lienig, Igor L. Markov, Jin Hu Lecture by Prof. John Reuben, VLSI Physical Design: From Graph Partitioning to Timing Closure Chapter 7: Specialized Routing Lienig VIT University, INDIA

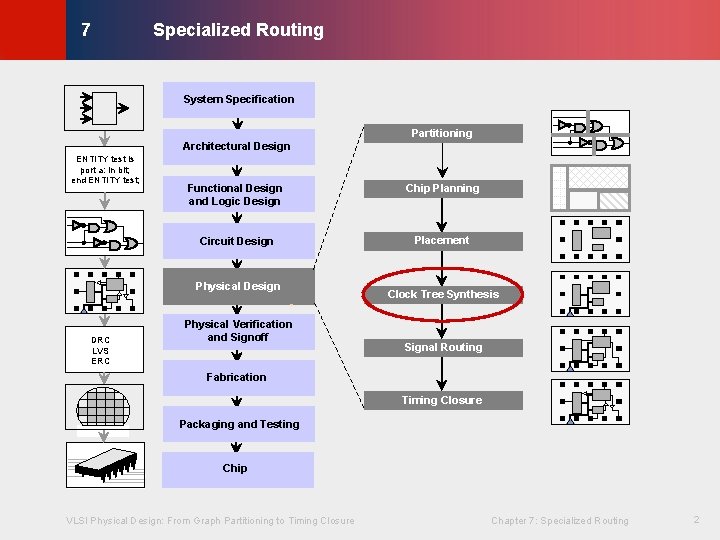
Specialized Routing © KLMH 7 System Specification Partitioning Architectural Design ENTITY test is port a: in bit; end ENTITY test; Functional Design and Logic Design Chip Planning Circuit Design Placement Physical Design DRC LVS ERC Physical Verification and Signoff Clock Tree Synthesis Signal Routing Fabrication Timing Closure Packaging and Testing VLSI Physical Design: From Graph Partitioning to Timing Closure Chapter 7: Specialized Routing 2 Lienig Chip

Basic Concepts in Clock Networks © KLMH 7. 4 7. 1 Introduction to Area Routing 7. 2 Net Ordering in Area Routing 7. 3 Non-Manhattan Routing 7. 3. 1 Octilinear Steiner Trees 7. 3. 2 Octilinear Maze Search 7. 4 Basic Concepts in Clock Networks 7. 4. 1 Terminology 7. 4. 2 Problem Formulations for Clock-Tree Routing 7. 5 Modern Clock Tree Synthesis VLSI Physical Design: From Graph Partitioning to Timing Closure Chapter 7: Specialized Routing 3 Lienig 7. 5. 1 Constructing Trees with Zero Global Skew 7. 5. 2 Clock Tree Buffering in the Presence of Variation

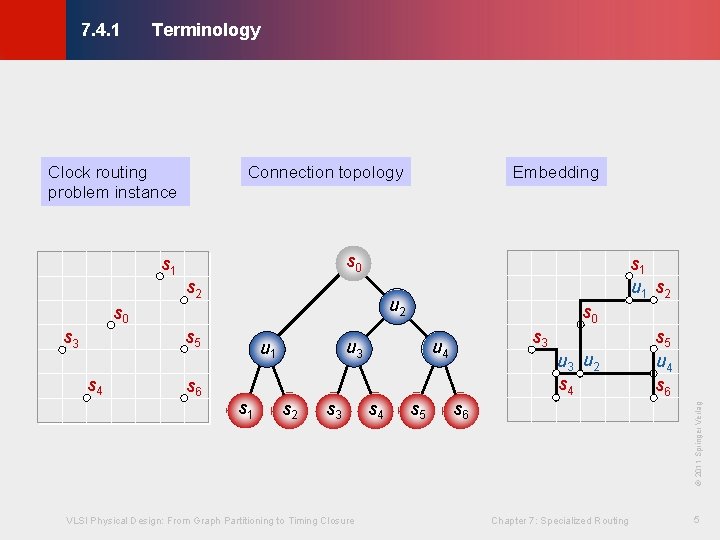
Terminology © KLMH 7. 4. 1 · A clock routing instance (clock net) is represented by n+1 terminals, where s 0 is designated as the source, and S = {s 1, s 2, … , sn} is designated as sinks - Let si, 0 ≤ i ≤ n, denote both a terminal and its location · A clock routing solution consists of a set of wire segments that connect all terminals of the clock net, so that a signal generated at the source propagates to all of the sinks - Two aspects of clock routing solution: topology and geometric embedding · The clock-tree topology (clock tree) is a rooted binary tree G with n leaves corresponding to the set of sinks VLSI Physical Design: From Graph Partitioning to Timing Closure Chapter 7: Specialized Routing 4 Lienig - Internal nodes = Steiner points

Terminology © KLMH 7. 4. 1 Connection topology s 0 s 1 s 2 s 6 u 3 u 1 s 0 s 2 s 3 VLSI Physical Design: From Graph Partitioning to Timing Closure s 3 u 4 s 5 u 3 u 2 s 4 s 6 s 5 u 4 s 6 © 2011 Springer Verlag s 5 s 4 s 1 u 1 s 2 u 2 s 0 s 3 Embedding Chapter 7: Specialized Routing 5 Lienig Clock routing problem instance

Terminology © KLMH 7. 4. 1 · Clock skew: (maximum) difference in clock signal arrival times between sinks · Local skew: maximum difference in arrival times of the clock signal at the clock pins of two or more related sinks - Sinks within distance d > 0 - Flip-flops or latches connected by a directed signal path · Global skew: maximum difference in arrival times of the clock signal at the clock pins of any two (related or unrelated) sinks - Difference between shortest and longest source-sink path delays in the clock distribution network VLSI Physical Design: From Graph Partitioning to Timing Closure Chapter 7: Specialized Routing 6 Lienig - The term “skew” typically refers to “global skew”

Problem Formulations for Clock-Tree Routing © KLMH 7. 4. 2 · Zero skew: zero-skew tree (ZST) - ZST problem · Bounded skew: true ZST may not be necessary in practice - Signoff timing analysis is sufficient with a non-zero skew bound - In addition to final (signoff) timing, this relaxation can be useful with intermediate delay models when it facilitates reductions in the length of the tree VLSI Physical Design: From Graph Partitioning to Timing Closure Chapter 7: Specialized Routing 7 Lienig - Bounded-Skew Tree (BST) problem

Modern Clock Tree Synthesis © KLMH 7. 5 7. 1 Introduction to Area Routing 7. 2 Net Ordering in Area Routing 7. 3 Non-Manhattan Routing 7. 3. 1 Octilinear Steiner Trees 7. 3. 2 Octilinear Maze Search 7. 4 Basic Concepts in Clock Networks 7. 4. 1 Terminology 7. 4. 2 Problem Formulations for Clock-Tree Routing 7. 5 Modern Clock Tree Synthesis VLSI Physical Design: From Graph Partitioning to Timing Closure Chapter 7: Specialized Routing 8 Lienig 7. 5. 1 Constructing Trees with Zero Global Skew 7. 5. 2 Clock Tree Buffering in the Presence of Variation

Modern Clock Tree Synthesis © KLMH 7. 5 · A clock tree should have low skew, while delivering the same signal to every sequential gate · Clock tree synthesis is performed in two steps: (1) Initial tree construction (Sec. 7. 5. 1) with one of these scenarios - Construct a regular clock tree, largely independent of sink locations - Simultaneously determine a topology and an embedding - Construct only the embedding, given a clock-tree topology as input VLSI Physical Design: From Graph Partitioning to Timing Closure Chapter 7: Specialized Routing 9 Lienig (2) Clock buffer insertion and several subsequent skew optimizations (Sec. 7. 5. 2)

Constructing Trees with Zero Global Skew © KLMH 7. 5. 1 H-tree - Blockages can spoil the symmetry of an H-tree - Non-uniform sink locations and varying sink capacitances also complicate the design of H-trees VLSI Physical Design: From Graph Partitioning to Timing Closure Chapter 7: Specialized Routing 10 Lienig · Used for top-level clock distribution, not for the entire clock tree © 2011 Springer Verlag · Exact zero skew due to the symmetry of the H-tree

© KLMH X Tree If routing is not restricted to being rectilinear, an X-tree structure can be used. Smaller Delay than H-Tree. VLSI Physical Design: From Graph Partitioning to Timing Closure Chapter 7: Specialized Routing Lienig Cross talk due to close proximity of wires.

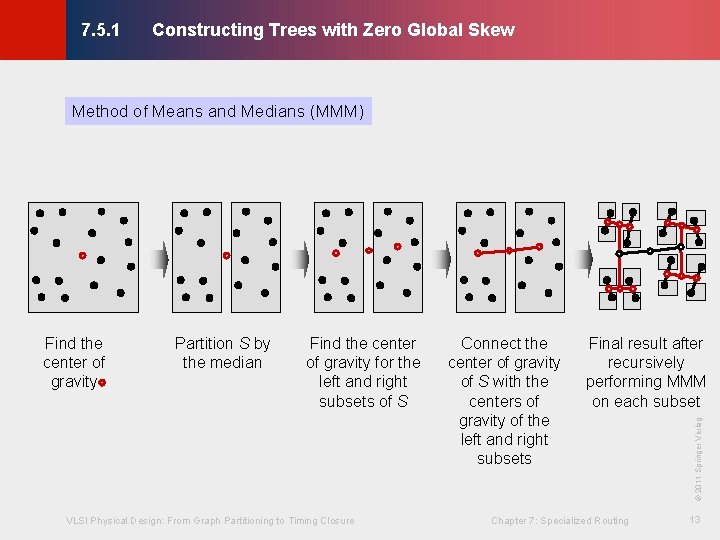
Constructing Trees with Zero Global Skew © KLMH 7. 5. 1 Method of Means and Medians (MMM) · Can deal with arbitrary locations of clock sinks · Basic idea: - Recursively partition the set of terminals into two subsets of equal size (median) - Connect the center of gravity (COG) of the set to the centers of gravity of the two subsets (the mean) Clock skew is only minimized. The resulting tree may not have zero-skew. VLSI Physical Design: From Graph Partitioning to Timing Closure Chapter 7: Specialized Routing 12 Lienig •

Constructing Trees with Zero Global Skew © KLMH 7. 5. 1 Method of Means and Medians (MMM) Find the center of gravity for the left and right subsets of S VLSI Physical Design: From Graph Partitioning to Timing Closure Connect the center of gravity of S with the centers of gravity of the left and right subsets Final result after recursively performing MMM on each subset Chapter 7: Specialized Routing © 2011 Springer Verlag Partition S by the median 13 Lienig Find the center of gravity

Constructing Trees with Zero Global Skew © KLMH 7. 5. 1 · S is the set of clock sinks in x-y plane · Calculate the center of mass of points in S. · Order the points in the increasing order of x-coordinate, Sx(S) · partition the original region in the x dimension into two sub-regions with approximately equal number of points in each sub-region(SL and SR). · Route from the center of mass of S to each of the centers of mass of SL and SR respectively. · The regions SL and SR are then recursively split in the y direction (the direction opposite to the previous one). VLSI Physical Design: From Graph Partitioning to Timing Closure Chapter 7: Specialized Routing 14 Lienig Method of Means and Medians (MMM)

· Basic MMM algorithm produces non-rectilinear tree. · Some wires may intersect eachother (more dense distributions of pins in some area can cause this) · In the second phase, each wire in the tree can be converted to a rectilinear tree and also intersections can be removed by another algorithm. VLSI Physical Design: From Graph Partitioning to Timing Closure Chapter 7: Specialized Routing Lienig © KLMH Second phase-refinements

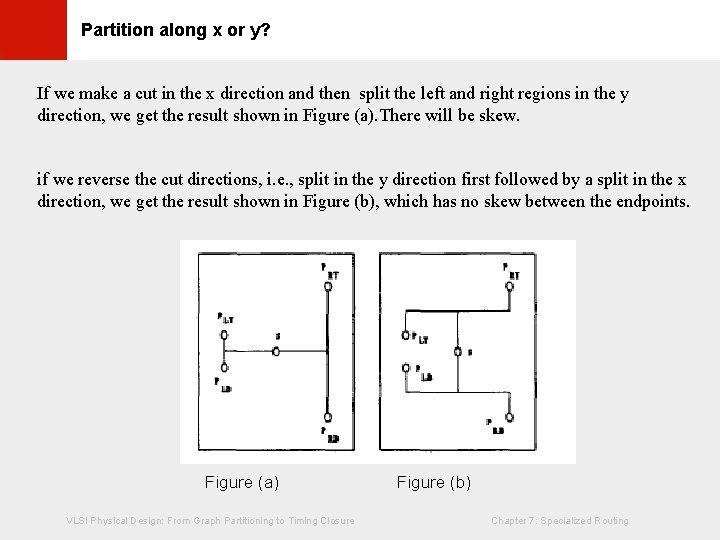
If we make a cut in the x direction and then split the left and right regions in the y direction, we get the result shown in Figure (a). There will be skew. © KLMH Partition along x or y? if we reverse the cut directions, i. e. , split in the y direction first followed by a split in the x direction, we get the result shown in Figure (b), which has no skew between the endpoints. VLSI Physical Design: From Graph Partitioning to Timing Closure Figure (b) Chapter 7: Specialized Routing Lienig Figure (a)

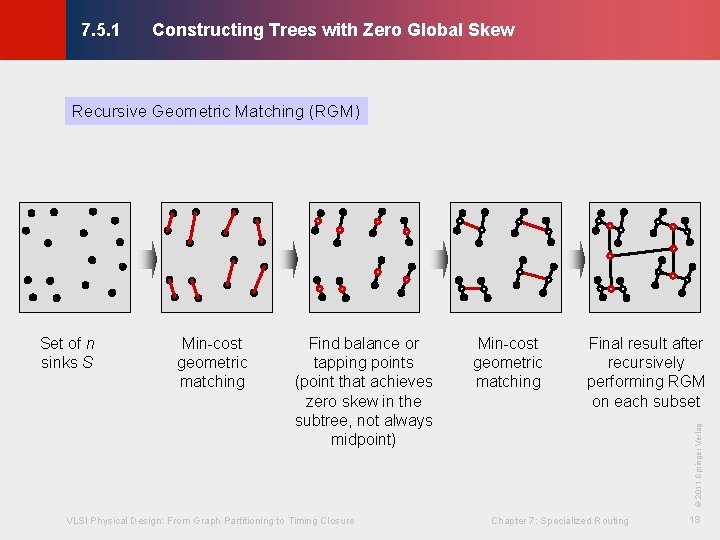
Constructing Trees with Zero Global Skew © KLMH 7. 5. 1 Recursive Geometric Matching (RGM) · RGM proceeds in a bottom-up fashion - Compare to MMM, which is a top-down algorithm · Basic idea: - Recursively determine a minimum-cost geometric matching of n sinks - Find a set of n / 2 line segments that match n endpoints and minimize total length (subject to the matching constraint) - After each matching step, a balance or tapping point is found on each matching segment to preserve zero skew to the associated sinks VLSI Physical Design: From Graph Partitioning to Timing Closure Chapter 7: Specialized Routing 17 Lienig - The set of n / 2 tapping points then forms the input to the next matching step

Constructing Trees with Zero Global Skew © KLMH 7. 5. 1 Recursive Geometric Matching (RGM) Find balance or tapping points (point that achieves zero skew in the subtree, not always midpoint) VLSI Physical Design: From Graph Partitioning to Timing Closure Min-cost geometric matching Final result after recursively performing RGM on each subset © 2011 Springer Verlag Min-cost geometric matching Chapter 7: Specialized Routing 18 Lienig Set of n sinks S

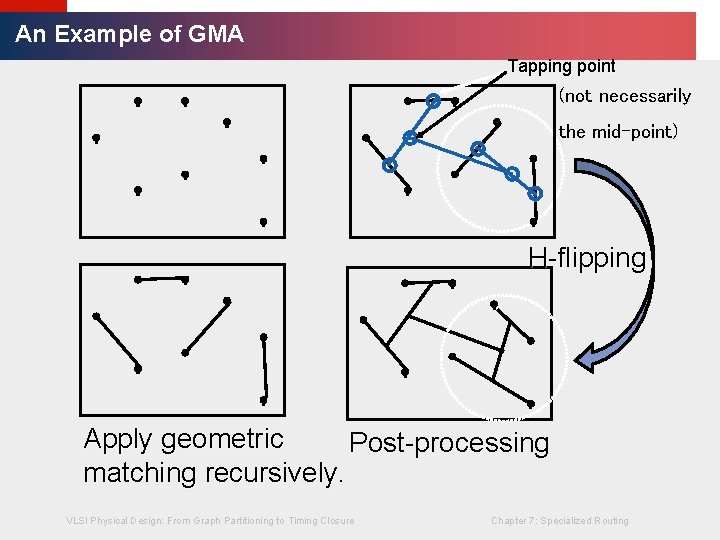
· GMA can achieve near zero average clock skew. · MMM is a top-down algorithm, but GMA is a bottom-up algorithm. VLSI Physical Design: From Graph Partitioning to Timing Closure Chapter 7: Specialized Routing Lienig © KLMH GMA

Tapping point (not necessarily © KLMH An Example of GMA the mid-point) H-flipping VLSI Physical Design: From Graph Partitioning to Timing Closure Chapter 7: Specialized Routing Lienig Apply geometric Post-processing matching recursively.