KLASSZIKUS KINETIKAI ALAPOK Pta Gyrgy Modern fizikai kmia

KLASSZIKUS KINETIKAI ALAPOK • Póta György: Modern fizikai kémia (Digitális Tankönyvtár, 2013), 2. 2 fejezet • P. W. Atkins: Fizikai kémia III. (Tankönyvkiadó, Budapest, 2002)

Reakciósebesség, sebességi egyenlet • A reakciók sztöchiometriai egyenletét – hasonlóan, mint a termodinamikában – itt is a jobb oldalra rendezve adjuk meg: 2 • A direkt reakcióra: • Általános esetben: a termék sztöchiometriai együtthatója és a kiindulási anyagé (reaktánsé). • Bevezetjük a következő mennyiséget:

Reakciósebesség, sebességi egyenlet • A kémiai reakcióban fellépő sztöchiometria miatt az egyes Bj anyagfajták anyagmennyisége időben egymással arányosan változik. Ez azt jelenti, hogy az mennyiség minden anyagfajtára (azaz a j indextől függetlenül) ugyanaz az érték. Itt nj a j-edik, Bj anyagfajta anyagmennyisége, t pedig az idő. Természetesen feltételezzük, hogy a reakcióban ténylegesen változó mennyiségű anyagfajtákról van szó, azaz νj ≠ 0. • A reakció sebessége: ahol V a reakcióelegy térfogata, cj pedig a j-edik anyagfajta moláris koncentrációja. Az így definiált reakciósebesség abszolút értéke független attól, hogy az egyenletben melyik anyagfajta adatai szerepelnek.

Reakciósebesség, sebességi egyenlet • A reakciósebesség a Bj anyagfajták anyagmennyiségének, a hőmérsékletnek és esetleg a nyomásnak a függvénye. A függvényt megadó sebességi egyenlet: ahol w–(c 1, c 2, …, c. N) > 0 és w+(c 1, c 2, …, c. N) > 0 az oda- és a visszareakció sebességét jelöli. A w, w– és w+ konkrét alakját elméleti megfontolások vagy kísérletek segítségével adhatjuk meg.

Reakciósebesség, sebességi egyenlet • Az ún. elemi reakciók esetében a reakcióegyenlet nem csupán a sztöchiometriai viszonyokat, hanem a molekuláris történést is kifejezi. Ebben az esetben a sztöchiometriai együtthatók együttese rögzített (nem szorozható meg egy tetszőleges szorzó tényezővel). Az elemi reakció sebességi egyenlete: valamint: és ahol k – > 0 az oda-, k+ > 0 a visszafelé irányuló reakció sebességi együtthatója. Ezt az egyenletet történeti okok miatt tömeghatás-típusú vagy Guldberg–Waage-egyenletnek szokás nevezni.

Reakciósebesség, sebességi egyenlet • Előfordul, hogy a visszafelé irányuló reakció sebessége elhanyagolható az oda irányuló reakcióéhoz képest. Az így létrejövő egyirányú reakció egyenletében a ⇌ megfordítható nyilat a → egyirányú nyíllal helyettesítjük, a sebességi egyenletben pedig elhagyjuk a w+ tagot.

Reakciósebesség, sebességi egyenlet • Amennyiben a reakciósebesség koncentrációfüggését leíró w sebességi egyenlet és a térfogat időfüggését megadó V(t) függvényértékek ismertek, a reakcióban szereplő anyagfajták koncentrációjának időbeli változását a következő differenciálegyenlet-rendszer írja le: ahol j = 1, 2, …, N • A megoldáshoz szükséges a kezdeti (t = 0 -ra vonatkozó) koncentrációk (cj(0) = c 0 j) ismerete. • Ha a V térfogat állandó, akkor:

Reakciósebesség, sebességi egyenlet • Egynél több reakció egyidejű (szimultán) lejátszódása esetén az eddig leírtakat általánosíthatjuk. • A rendszerben lejátszódó, i-edik reakció általános alakja: ahol i = 1, 2, …, M ahol νij– ≥ 0 a Bj reaktáns sztöchiometriai együtthatója, νij+ ≥ 0 pedig a Bj terméké. Ha a j-edik anyagfajta valóban szerepel az i-edik reakcióban, akkor sztöchiometriai együtthatója pozitív, egyébként 0. • Az egyes anyagfajták koncentrációjának időbeli változását leíró kezdetiérték-feladat ekkor: és cj(0) = c 0 j

Reakciósebesség, sebességi egyenlet • Előfordul, hogy egy reakciórendszerben egyszerre több elemi reakció megy végbe, viszont az összetétel változása egyetlen „bruttó” reakcióegyenlettel és a hozzá tartozó „bruttó” sebességi egyenlettel kielégítően leírható. Ekkor összetett reakcióról beszélünk, amelynek mechanizmusán a háttérben futó elemi reakciók összességét értjük. Erről a „Reakciómechanizmusok analízise” témakörben részletesebben is szó lesz. • Összetett reakcióknál a sebességi egyenlet sokféle alakú lehet. Külön említést érdemel a következő (elemi reakcióhoz hasonló): Itt azonban az αj kitevőkre – az egyes anyagfajtákra vonatkozó részrendekre – nincsenek szigorú kikötések.

A kinetikai differenciálegyenletek és cj(0) = c 0 j (2 -vel korábbi slide) • A kinetikai differenciálegyenlet-rendszer megoldása csak akkor fogadható el, ha nemnegatív kezdeti értékből indulva t > 0 esetén nemnegatív marad. • A megoldásnak a teljes t > 0 tengelyre értelmezve kell lennie. • A kinetikai differenciálegyenletek megoldásának létezése, pozitivitása és korlátossága a matematika által nyújtott eszközökkel precízen és általánosan vizsgálható. • Léteznek eredmények a változó T rendszerekre is.

A kinetikai differenciálegyenletek és cj(0) = c 0 j • A megoldás analitikus alakban (tehát véges képlettel) biztosan előállítható, ha az egyenlet jobb oldala az ismeretlenek lineáris függvénye. Ez a lineáris differenciálegyenletekre vonatkozó tételekből következik. • A nemlineáris jobb oldalú rendszerek csak egyszerű esetekben oldhatók meg analitikusan. Ilyen például a következő állandó térfogatú rendszer: X+Y→Z w = k[X][Y] (A koncentrációt a szokásos módon szögletes zárójellel jelöltük. )

A kinetikai differenciálegyenletek – Nemlineáris jobb oldalú rendszerek X+Y→Z w = k[X][Y] • A kinetikai differenciálegyenletek: • A kezdeti feltételek (t = 0 időpontban): [X](0) = [X]0 [Y](0) = [Y]0 [Z](0) = [Z]0 • A rendszer egyszerűsítése céljából felhasználjuk, hogy a megoldás teljes értelmezési intervallumán , így [X] – [Y] = [X]0 – [Y]0 • Ezt felhasználva: [Y] = [Y]0 – [X]0 + [X] és

A kinetikai differenciálegyenletek – Nemlineáris jobb oldalú rendszerek X+Y→Z w = k[X][Y] • Ebben már csak egyetlen ismeretlen függvény ([X]) szerepel. A szeparálható változójú differenciálegyenlet megoldása: ahol [Y]0 – [X]0 ≠ 0 • Ebből [X] a t idő függvényeként kifejezhető, ezt felhasználva pedig [Y] = [Y]0 – [X]0 + [X] és (mivel [Z] + [X] = [Z]0 + [X]0) [Z] = [Z]0 + [X]0 – [X] is megadható.

A kinetikai differenciálegyenletek • A bonyolult kinetikai rendszerekben – amelyek rendszerint sok egyszerre lejátszódó reakciót tartalmaznak – az összetétel változása célszerűen a kinetikai differenciálegyenletek numerikus megoldásával határozható meg. (Ez sem mindig könnyű feladat, mert a kinetikai differenciál-egyenletek sok esetben nehezen kezelhető, ún. „merev” („stiff”) rendszerek. )

A reakciókinetika feladata • A reakciókinetika direkt feladata az, hogy a lejátszódó reakciók és sebességi egyenleteik ismeretében megadja a rendszer összetételének (és esetleg hőmérsékletének, nyomásának) időbeli változását. • Az ipari és egyéb alkalmazások során rendszerint a direkt feladat megoldására van szükség. Az ehhez szükséges egyenleteket az előző pontokban már áttekintettük. • Jelenleg még nem ismerünk olyan törvényt, amely megadná, hogy adott reaktánsok összekeverésekor milyen kémiai reakciók fognak létrejönni. A reakciókinetikai kutatások során a legtöbb esetben a mért időbeli adatok (pl. koncentrációk) segítségével megpróbáljuk meghatározni, hogy milyen sztöchiometriájú és sebességű kémiai reakciók játszódnak le a vizsgált rendszerben. Ez a reakciókinetika inverz feladata.

A reakciókinetika feladata • Az egyszerűbb reakciók felderítésére alkalmas, főként grafikus módszerekkel Fizikai Kémia II. -n foglalkoztunk. • A bonyolult kinetikai rendszereket általában számítógép segítségével tanulmányozzuk. A mérési adatok illesztésénél a következő célfüggvényt szokás használni: ahol p = (p 1, p 2, …, pm) a paraméterek vektora, N a mérési adatpontok száma, yjexp a j-edik mért adatpont, σ(yjexp) a j-edik kísérleti adatpont szórása, yjm a j-edik adatpontnak megfelelő, p paraméterkészlettel számított érték. • A feladat megtalálni azt a p paramétervektort, amelynél a legkisebb az E(p) célfüggvény értéke.

A reakciókinetika feladata • Gyakran felmerülő nehézség, hogy az E(p) célfüggvénynek több minimumhelye van. Ekkor a globális minimumot kell megtalálni. • Szintén gyakori, hogy a kémiai feladat meghatározza, hogy az optimális paramétervektort a p mely tartományában kell keresni. • A célfüggvény használata esetén a méréseket a legkisebb négyzetes eltérés szerint legjobban leíró paraméterkészletet keressük. Mivel a mért adatok szórnak, emiatt nem várható, hogy minden adatot pontosan leírjon a modell (ez az E(p) = 0 esetnek felelne meg). Ha nagyon jó a modell egyezése a mérési adatokkal (tehát a mérési adatok eltérését a modelltől csak a mérési adatok szórása okozza), akkor E(p) ≈ 1.

Hőmérsékletfüggés • A tapasztalat szerint a reakciósebesség függ a T-től. Számos esetben jó közelítéssel érvényes az eredeti Arrhenius-egyenlet: • Széles (több száz K) hőmérséklettartományban ez általában már nem alkalmazható és ilyenkor az ún. kiterjesztett Arrhenius-egyenletet szokták használni:

Hőmérsékletfüggés • Az eredeti Arrhenius-egyenlet viszonylag egyszerű magyarázatát adja az ütközési elmélet, amely a gázfázisú A+B→P w = k[A][B] reakció sebességi együtthatóját a következőképpen adja meg: ahol P a sztérikus faktor, σ a két molekula ütközési hatáskeresztmetszete, μ a redukált tömeg, k. B a Boltzmann-állandó, T a termodinamikai hőmérséklet, NA az Avogadro-állandó, R a gázállandó, Ea az aktiválási energia. • P az ütköző molekulák egymáshoz viszonyított helyzetét veszi figyelembe. • σ értéke RA és RB sugarú, merev gömb alakú részecskék esetén: • μ az A és B részecske m. A és m. B tömegéből számítható ki: Az ütközési elmélet hátránya, hogy P és Ea értékét paraméterként kezeli, azokat kiszámítani nem képes.

Hőmérsékletfüggés • Az átmeneti komplex elmélete összefüggést teremt a sebességi együttható és a reagáló részecskék, valamint a belőlük képződő átmeneti komplex anyagszerkezeti adatai között. • A gázfázisú A + B ⇌ C# → P reakcióra az Eyring-egyenlet értelmében: ahol κ a transzmissziós tényező, h a Planck-állandó, p 0 a standard nyomás, ΔE 0 a nullponti energiák különbsége, q. A 0, q. B 0 és q. C 0 az A, B és C# részecskék állapotösszegei (amelyek a részecskék transzlációs, rotációs és vibrációs állapotösszegeinek szorzatát jelentik). A – vonal azt jelenti, hogy a q. C 0 állapotösszegből a C# széteséséhez vezető rezgés állapotösszegét leválasztottuk.

Hőmérsékletfüggés • Főként az ipari gyakorlatban változó hőmérsékletű kinetikai rendszerekkel is találkozunk. Ekkor a kinetikai differenciálegyenletekhez a hőmérséklet változását leíró egyenlet is társul: A Jq hőáram hőszigetelt rendszerben nulla, egyébként pedig gyakran arányos a rendszer és a környezet hőmérsékletének különbségével. Az egyenletben szerepelnek a wi reakciósebességek, amelyek függenek a hőmérséklettől. A változó hőmérsékletű rendszerek tényleges szimulációjához szükséges, hogy ezt a függést megadjuk.

KINETIKAI EGYSZERŰSÍTŐ ELVEK • Póta György: Modern fizikai kémia (Digitális Tankönyvtár, 2013), 2. 5. 3 fejezet • P. W. Atkins: Fizikai kémia III. (Tankönyvkiadó, Budapest, 2002)

Kinetikai egyszerűsítő elvek • A kinetikai egyszerűsítő elvek segítségével egy bonyolult mechanizmus (vagy annak kinetikai differenciálegyenlet-rendszere) egyszerűsíthető. • Ha egy kinetikai differenciálegyenlet-rendszert a megmaradó mennyiségek figyelembe vételével egyszerűsítenek, akkor az egyszerűsített modell eredménye pontosan azonos lesz az eredeti modellével. • A nagy feleslegben alkalmazott reaktáns, a gyors előegyensúly, a sebesség-meghatározó lépés és a kvázistacionárius közelítés eltérő módon, de mind a reakciókinetikai modellben levő nagyon különböző időskálák létezését használják fel. Az így kapott szimulációs eredmények nem azonosak az eredeti mechanizmussal kapott megoldással, de a hiba kicsi (1% alatti).

Megmaradó mennyiségek • Sok reakciómechanizmus olyan rendszert ír le, amelyben megmaradó mennyiségek vannak. • Zárt rendszerben ilyen a rendszer összes tömege, az anyagfajták • • anyagmennyiségének összege (ha minden reakciólépésre teljesül, hogy az anyagmennyiség-változás a reakciólépés során nulla). Állandó térfogatú rendszerben a moláris koncentrációk összege is állandó. Zárt rendszerben kémiai reakciók nem változtathatják meg az elemek anyagmennyiségét, tehát minden elemre külön-külön az összes anyagmennyiségük megmaradó mennyiség. Megmaradó mennyiség az összes entalpia adiabatikus rendszerben, …vagy a töltés elektrokémiailag zárt rendszerekben. Ugyancsak megmaradó mennyiségként jelenik meg, ha egy atomcsoport nem változik meg a reakciólépések során (megmaradó atomcsoport). Ilyen lehet például az adenozin-csoport; ekkor az AMP, ADP és ATP összege a zárt biokémiai reakciórendszerben állandó.

Megmaradó mennyiségek • Ha egy NS anyagfajtát tartalmazó mechanizmusban NC megmaradó mennyiséget lehet azonosítani, akkor a kinetikai differenciálegyenlet-rendszernek N = NS – NC független változója van. • Ekkor tehát elegendő N anyagfajta koncentrációját számítani a differenciálegyenlet-rendszer megoldásával, és a többi NC anyagfajta koncentrációja a megmaradó mennyiségek kezdeti értéke alapján számítható. • A kinetikai differenciálegyenlet-rendszer változói számának csökkentése a megmaradó mennyiségek alapján nem közelítés, ilyenkor az eredetivel pontosan azonos megoldást kapunk.

Megmaradó mennyiségek Példa: • Az A → B → C sorozatos elsőrendű reakciórendszerben mindkét reakciólépés során a reakcióegyenlet bal és jobb oldalán az anyagfajták anyagmennyisége megegyezik. A reakciólépések során tehát az anyagmennyiség megőrződik, emiatt állandó térfogatú zárt rendszerben minden t időpillanatban: [A](t) + [B](t) + [C](t) = [A]0 + [B]0 + [C]0 • Elegendő tehát csak az A és B anyagfajták koncentráció– idő függvényét számítanunk, ebből C koncentrációja minden időpontban számítható: [C](t) = [A]0 + [B]0 + [C]0 – [A](t) – [B](t)

Nagy feleslegben alkalmazott reaktáns • A „nagy feleslegben alkalmazott reaktáns”-közelítés akkor alkalmazható, ha az egyik reaktánsból olyan sok van jelen, hogy a reakció során koncentrációja elhanyagolható mértékben változik meg, és így állandónak tekinthető. Ennek alapján pl. másodrendű reakciólépés elsőrendűvé alakítható át, és ebben a speciális esetben a módszer neve pszeudo-elsőrendű közelítés. X+Y→Z w = k[X][Y] • A megoldás az [X]0 ≠ [Y]0 esetre: [Y] = [Y]0 – [X]0 + [X] és [Z] = [Z]0 + [X]0 – [X]

Nagy feleslegben alkalmazott reaktáns • Sokkal könnyebb dolgunk van, ha [X]0 << [Y]0, mert ekkor Y koncentrációja a reakció végéig alig változik. Ekkor bevezethetünk egy új k′=k [Y]0 sebességi együtthatót, ami az X → Z reakcióhoz tartozik. E reakció következtében az X koncentrációja elsőrendű kinetika szerint csökken: • Az X koncentrációjának lecsengéséből minden Y koncentrációhoz kiszámítják a pszeudo-elsőrendű k′ sebességi együtthatót, majd az [Y] - k′ adatpárokból, egyenest illesztve határozzák meg a k másodrendű sebességi együtthatót: [X] k′ Meredekség = k [Y] idő

Nagy feleslegben alkalmazott reaktáns • A módszer előnye, hogy nem kell az [X] abszolút értékét megmérni, elég az X koncentrációjával arányos jelet mérni a kísérletben (például fényelést vagy fluoreszcens jelet); ekkor az exponenciális lecsengési görbe illesztésével már meghatározható a k′ együttható. [X]-val arányos jel [X] idő

Nagy feleslegben alkalmazott reaktáns Példa: • Az ·OH + C 2 H 6 = ·C 2 H 5 + H 2 O gázfázisú elemi reakció sebességi együtthatóját szeretnénk meghatározni. A kezdeti reakcióelegyben C 2 H 6 és HNO 3 van Ar hígítógázban. • A C 2 H 6 és a HNO 3 nem reagál egymással, de a 193 nm hullámhosszú lézerfény villanása a salétromsav egy részét elbontja, és a HNO 3 + hν = ·OH + NO 2 reakcióban OH-gyökök képződnek. • Ha a lézervillanás után az OH-gyök és a C 2 H 6 összemérhető koncentrációban lenne jelen, akkor az OH-gyök abszolút koncentrációját kellene mérni, ami nehéz feladat.

Nagy feleslegben alkalmazott reaktáns Példa: • Az ·OH + C 2 H 6 = ·C 2 H 5 + H 2 O gázfázisú elemi reakció sebességi együtthatóját szeretnénk meghatározni. A kezdeti reakcióelegyben C 2 H 6 és HNO 3 van Ar hígítógázban. • A C 2 H 6 és a HNO 3 nem reagál egymással, de a 193 nm hullámhosszú lézerfény villanása a salétromsav egy részét elbontja, és a HNO 3 + hν = ·OH + NO 2 reakcióban OH-gyökök képződnek. • Ehelyett az C 2 H 6 -t változó, de ismert koncentrációban, több ezerszeres feleslegben alkalmazzák. Ekkor elegendő olyan módszer választani (pl. fluoreszcens fény erősségének mérése), amivel az OH-gyök koncentrációjával arányos jelet mérhetünk.

Nagy feleslegben alkalmazott reaktáns Példa: Az C 2 H 6 -t nagy koncentrációban alkalmazzák, majd a mért exponenciális görbe illesztésével meghatározzák az adott C 2 H 6 koncentrációhoz tartozó k′ pszeudo-elsőrendű sebességi együtthatót.

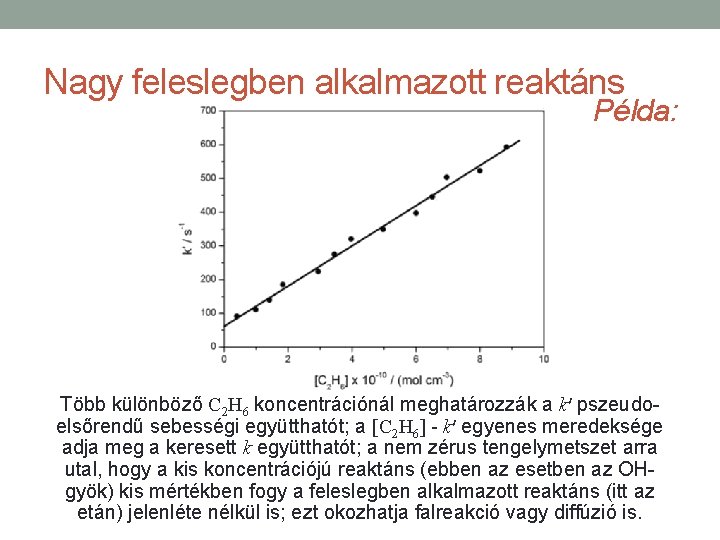
Nagy feleslegben alkalmazott reaktáns Példa: Több különböző C 2 H 6 koncentrációnál meghatározzák a k′ pszeudoelsőrendű sebességi együtthatót; a [C 2 H 6] - k′ egyenes meredeksége adja meg a keresett k együtthatót; a nem zérus tengelymetszet arra utal, hogy a kis koncentrációjú reaktáns (ebben az esetben az OHgyök) kis mértékben fogy a feleslegben alkalmazott reaktáns (itt az etán) jelenléte nélkül is; ezt okozhatja falreakció vagy diffúzió is.

Gyors előegyensúly • A „gyors előegyensúly”-közelítés akkor alkalmazható, ha egy gyors egyensúlyi reakciólépés-pár anyagfajtáit lassú reakciók fogyasztják vagy termelik. • Beállt egyensúly esetén az odairányú és a visszairányú reakciók sebessége egymással egyenlő, emiatt a részt vevő anyagfajták koncentrációinak aránya számítható a reakciólépések sztöchiometriája és az egyensúlyi állandó alapján. • Feltételezzük, hogy ha az egyensúlyi reakciólépések sebessége jóval nagyobb, mint az egyéb reakciólépéseké, akkor az egyensúlyi reakcióban résztvevő reaktánsok és termékek koncentrációaránya ugyanúgy számítható, mintha a lassú reakciólépések nem is lennének ott.

Gyors előegyensúly Példa: • Egy X ⇌ Y egyensúlyi reakció sebességi együtthatói k 1 és k-1, az egyensúlyi állandó pedig: K 1 = k 1/k-1. • Beállt egyensúly esetén az ellentétes irányú folyamatok sebessége azonos: k 1 [X] = k-1 [Y], így [Y] = (k 1/k-1)[X] = K 1 [X]. • Tegyük fel, hogy az Y reaktánst egy harmadik, az előző kettőnél sokkal lassabb reakció is fogyasztja, aminek a sebességi együtthatója k 2. A „gyors előegyensúly”-közelítés szerint ebben az X ⇌ Y → Z reakciórendszerben is jó közelítéssel [Y] = K 1 [X]. Ez azt jelenti, hogy: • Az enzimkinetikai mechanizmusoknál különösen gyakori, hogy a termék keletkezésének k′ = k 2 K 1 sebességi együtthatóját úgy adják meg, mint az enzim két (kevésbé reaktív X és nagyon reaktív Y) formája közötti átalakulást jellemző K 1 egyensúlyi állandó és a B továbbalakulását jellemző k 2 sebességi együttható szorzatát.

Sebesség-meghatározó lépés • Sebesség-meghatározó lépésnek nevezik azt a reakciólépést, aminek értéke meghatározza a termék keletkezési sebességét. • Ha a végtermék elsőrendű reakciók sorozatán keresztül keletkezik a kiindulási anyagból, akkor a legkisebb sebességi együtthatójú reakció lesz a sebesség-meghatározó lépés. • Tetszőleges mechanizmus esetén az a reakciólépés a sebességmeghatározó, amelyik sebességi együtthatójának kis megváltoztatására a végtermék termelődési sebessége jelentősen megnő. Ez általában nem a legkisebb sebességi együtthatójú reakció! • Ha egy végtermék koncentrációjának számítjuk a normált lokális érzékenységi együtthatóit (lásd később), akkor azt tapasztaljuk, hogy a legnagyobb érzékenységi együtthatónak megfelelő reakciólépés a sebesség-meghatározó.

Sebességmeghatározó lépés Példa: • Tegyük fel, hogy az F végtermék az A kiindulási anyagból sorozatos elsőrendű reakciók útján keletkezik: • A C anyag keletkezését a B anyagból a d[C]/dt = k 2[B] egyenlet írja le. Ha azonban k 2 << k 1, k 3, k 4, k 5, akkor a keletkező C anyag nagyon gyorsan továbbalakul, és hamarosan F keletkezik belőle. Ennek az F anyagnak a keletkezése is leírható tehát a d[F]/dt = k 2 [B] egyenlettel. • Tehát ha k 1, k 3, k 4 és k 5 sokkal nagyobb, mint k 2, akkor az F keletkezési sebességét csak k 2 értéke szabja meg. • Így F és B koncentrációváltozásának mérésével csak a k 2 sebességi együtthatót lehet meghatározni. Láthatjuk azt is, hogy elsőrendű reakciósorozatban nem feltétlenül az első reakció a sebességmeghatározó.

Kvázistacionárius közelítés • A kvázistacionárius közelítést annak egyik első alkalmazója után szokás Bodenstein-elvnek, illetve angol nevének (quasi steady-state approximation) rövidítése után QSSAnak nevezni.

Kvázistacionárius közelítés • A módszer lényege: 1. A reakciómechanizmus anyagfajtái közül kiválasztunk egyeseket, amelyeket a többitől eltérően kezelünk és amelyeket a továbbiakban kvázistacionárius (QSSA-) anyagoknak fogunk nevezni. A QSSA-anyagok általában nagy reaktivitású és kis koncentrációjú köztitermékek, mint pl. a gyökök. 2. Az ezen anyagok koncentrációváltozását leíró differenciálegyenletekben a bal oldalt nullával tesszük egyenlővé. A kapott egyenletek egy algebrai (tehát nem differenciál-) egyenletrendszert alkotnak, amely megadja, hogyan függ a QSSA-anyagok koncentrációja a többi (nem QSSA-) anyag koncentrációjától.

Kvázistacionárius közelítés • A módszer lényege: 3. A nem QSSA-anyagokra vonatkozó differenciálegyenletrendszer és a QSSA-anyagokra vonatkozó algebrai egyenletrendszer együtt úgynevezett csatolt differenciál-algebrai egyenletrendszert ad. Ezt az egyenletrendszert megoldva az eredeti kinetikai differenciálegyenlet-rendszerével csaknem azonos megoldást kaphatunk, amennyiben helyesen választottuk ki a kvázistacionárius anyagfajtákat. 4. Szerencsés esetben az algebrai egyenletrendszer külön is megoldható, tehát az egyes QSSA-anyagfajták koncentrációját explicit algebrai egyenletekkel ki tudjuk számítani, és ezeket az explicit algebrai egyenleteket be tudjuk írni a nem QSSAanyagok differenciálegyenlet-rendszerébe. Gyakran, de nem mindig, a kapott differenciálegyenlet-rendszernek meg tudunk feleltetni egyszerűbb reakciómechanizmust.

Kvázistacionárius közelítés • A kvázistacionárius közelítés úgy is felfogható, hogy a nemkvázistacionárius anyagfajták koncentrációjából algebrai úton kiszámítható az összes kvázistacionárius anyagfajta koncentrációja. Bármi volt kezdetben a kvázistacionárius anyagfajták koncentrációja, előbb-utóbb ezek a koncentrációk a QSSA-közelítésből kapott algebrai egyenletek megoldásából adódó értékek közelében lesznek. A kvázistacionárius közelítés kulcsa, hogy mely anyagokat választjuk kvázistacionárius anyagfajtának, és hogy mekkora hibát követünk el a QSSA alkalmazásával.

Kvázistacionárius közelítés Összefüggés egy anyagfajta koncentrációja, annak koncentrációváltozási sebessége, és a QSSA- és a valódi koncentráció különbsége, tehát a kvázistacionárius közelítés hibája között.

Kvázistacionárius közelítés Példa: • A kvázistacionárius közelítés szokásos alappéldája: • Ha k 2>>k 1, akkor a B anyag nagyon gyorsan reagál, és alkalmazható rá a kvázistacionárius közelítés. Ekkor B koncentrációját nem a d[B]/dt = k 1[A]−k 2[B] differenciálegyenlettel, hanem a következő algebrai egyenlettel számítjuk: 0 = k 1[A] − k 2[B] • Ebből B koncentrációja kifejezhető: Mivel a kiindulási feltételezésünk szerint k 2 >> k 1, ezért B koncentrációjának lefutása hasonló alakú lesz, mint A-é, csak sokkal kisebb értékekkel. Nyilvánvaló, hogy ha [B]0 kezdeti értéke nulla volt, akkor ez csak egy bizonyos időtartam (az úgynevezett „indukciós periódus”) letelte után teljesülhet.