KKL KruskalKatona and Monotone Nets Ryan ODonnell Karl

KKL, Kruskal-Katona, and Monotone Nets Ryan O’Donnell Karl Wimmer Carnegie Mellon University & Duquesne University

Monotone. Nets

Monotone. Nets H is a γ-net for monotone functions if: ∀ monotone f : {0, 1}n → {0, 1}, ∃ h ∈ H s. t. corr[h, f]≥ γ. monotone: x ≤ y ⇒ f(x) ≤ f(y)

Monotone. Nets H is a γ-net for monotone functions if: ∀ monotone f : {0, 1}n → {0, 1}, ∃ h ∈ H s. t. corr[h, f]≥ γ. corr[h, f] = Pr[ h(x) = f(x) ] − Pr[ h(x) ≠ f(x) ] dist[h, f] = ½ − ½ corr[h, f]

who what [KV 89] {0, 1, x 1, …, xn} γ ≥ Ω( 1 / n ) [BT 95] {0, 1, x 1, …, xn} γ = Θ( log n / n ) [BBL 98] {0, 1, Maj} γ = Θ( this work {0, 1, x 1, …, xn, Maj} ≥ Θ( Ω( γ= ) γ ≤ O( ) [BBL 98] any |H| = poly(n) how much )

who what why [KV 89] {0, 1, xlearning Weak 1, …, xn} γ ≥ Ω( 1 / n ) [BT 95] {0, 1, x 1, …, xn} γ = Θ( log n / n ) [BBL 98] {0, 1, Maj} γ = Θ( this work {0, 1, x 1, …, xn, Maj} γ = Θ( ) γ ≤ O( ) [BBL 98] any |H| = poly(n) how much )

Cor: [OW 09] Weak learning Monotone functions are weakly-learnable with advantage Ω( under the uniform distribution. )

Weak learning Cor: [OW 09] Monotone functions are weakly-learnable with advantage Ω( under the uniform distribution. Proof: Draw O(n / log n) examples (x, f(x)). Output most correlated-seeming function in the net. )

Weak learning Cor: [OW 09] Monotone functions are weakly-learnable with advantage Ω( ) under the uniform distribution. Proof: Draw O(nϵ) examples (x, f(x)). Output 0, 1, x 1, …, or xn if it seems good. Else output Maj.

who what [KV 89] {0, 1, x 1, …, xn} γ ≥ Ω( 1 / n ) [BT 95] {0, 1, x 1, …, xn} γ = Θ( log n / n ) [BBL 98] {0, 1, Maj} γ = Θ( this work {0, 1, x 1, …, xn, Maj} γ = Θ( ) γ ≤ O( ) [BBL 98] any |H| = poly(n) how much )

Weak learning Cor: [OW 09] Monotone functions are weakly-learnable with advantage Ω( ) under the uniform distribution. Thm: [BBL 98] Any learning alg. for monotone functions which sees only poly(n) examples achieves advantage O( ).

who what how [KV 89] {0, 1, x 1, …, xn} γ ≥ Ω( 1 / n ) [BT 95] {0, 1, x 1, …, xn} γ = Θ( log n / n ) [BBL 98] {0, 1, Maj} γ = Θ( this work {0, 1, x 1, …, xn, Maj} γ = Θ( ) γ ≤ O( ) [BBL 98] any |H| = poly(n) how much )

who how [KV 89] Expansion [BT 95] KKL Theorem [BBL 98] Kruskal-Katona γ = Θ( this work Generalized KKL γ = Θ( ⇒ how much γ ≥ Ω( 1 / n ) γ = Θ( log n / n ) ⇒ Robust Kruskal-Katona ) )

Part 1: The KKL Theorem

Kahn-Kalai-Linial Theorem [KKL 88] For f : {0, 1}n → {0, 1}, Def: ∃ i ∈ [n] s. t.

x 101001010000001 0 000101000101 1

) ity ic 0 000101000101 0 1 1 0 on 101001010000001 ot x on (m f(x) KKL: for some i

who how [KV 89] Expansion [BT 95] KKL Theorem [BBL 98] Kruskal-Katona γ = Θ( this work Generalized KKL γ = Θ( ⇒ how much γ ≥ Ω( 1 / n ) γ = Θ( log n / n ) ⇒ Robust Kruskal-Katona ) )

Expansion Theorem for the hypercube

Expansion Theorem for the hypercube

Expansion Theorem for the hypercube

Expansion:

Expansion: KKL refined: [Talagrand] If Inf i [f] ≤ 1/n. 01 for all i, then Tight: “Tribes” is monotone, has corr. O(log n / n) with 0, 1, x 1, …, xn.

KKL • No known combinatorial proof • (log n) may look small, but → ∞ • why a o(1) frac. voters can control any 2 -party election [KKL 88] • why monotone graph properties have sharp thresholds [FK 96] • why Sparsest-Cut SDP has superconstant integrality gap [DKSV 06]

KKL: Proof sketch Expansion Theorem is not tightfor tiny sets. Apply this idea to each set ∂ i f = {x : f(x) ≠ f(x(i))}.

KKL: Proof sketch Expansion Theorem is not tightfor tiny sets. Apply this idea to each set ∂ i f = {x : f(x) ≠ f(x(i))}. [Harper’ 64]: Look at g(x) : = Pr[ short rand. walk from x in ∂ i f ]. Generalize [Har 64] to g : {0, 1}n → ℝ, “Log-Sobolev Inequality”[Gross’ 75]

Intermission

KKL, Kruskal-Katona, and Monotone Nets Ryan O’Donnell Karl Wimmer Carnegie Mellon University & Duquesne University

Kruskal-Katona Theorem “Slice”: Def: If f monotone, μk+1 ≥ complicated-fcn(μk, k) KK Thm. gives exact minimizer for each μk.

Corollary of KK: [Lov 79, BT 87] If f monotone

Corollary of KK: Tight: If f(x) = xi, f monotone

Implies [BBL 98]: {0, 1, Maj} is -net. Sketch: Assume μn/2 = 1/2. KK … Ω(1) prob. mass

[us]: {0, 1, x 1, …, xn, Maj} is Robust Kruskal-Katona Thm: Let f be monotone, If corr then [f, xi] ≤ 1/n. 01 ∀ i, -net.

Similar to KKL, but localizedto a slice. Robust Kruskal-Katona Thm: Let f be monotone, If corr then [f, xi] ≤ 1/n. 01 ∀ i,

Similar to KKL, but localizedto a slice. thm: “KKL on Let f : ” → {0, 1}. If Inf ij [f] ≤ 1/n. 01 for all i, j, then

Summary: ? thm: “KKL on ⇒ ✔ Robust Kruskal-Katona ✔ ⇒ ✔ Net Theorem for mono. fcns ✔

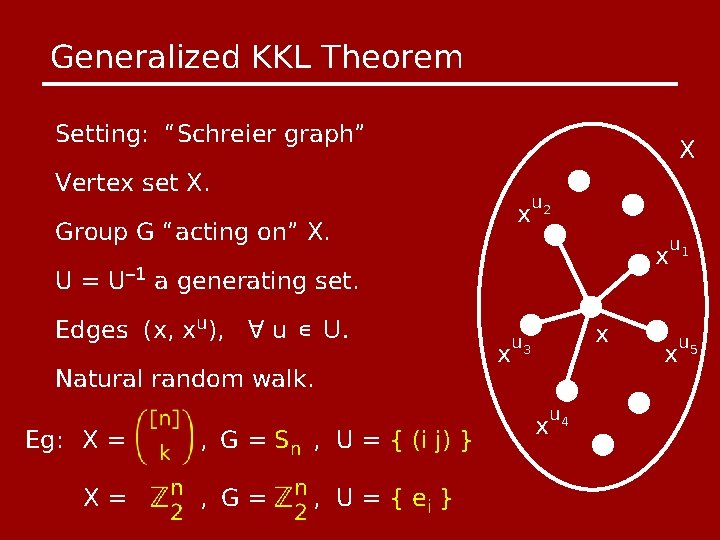
Generalized KKL Theorem Setting: “Schreier graph” X Vertex set X. x Group G “acting on” X. u 2 x U = U– 1 a generating set. Edges (x, xu), ∀ u ∈ U. Natural random walk. Eg: X = X= , G = Sn , U = { (i j) } , G= , U = { ei } x x u 3 x u 4 u 1 x u 5

Can carry out KKL proof assuming… U is closed under conjugation (u v u− 1 ∈ U ∀ u, v ∈ U) , { ei }: abelian , { (i j) }: conj. class

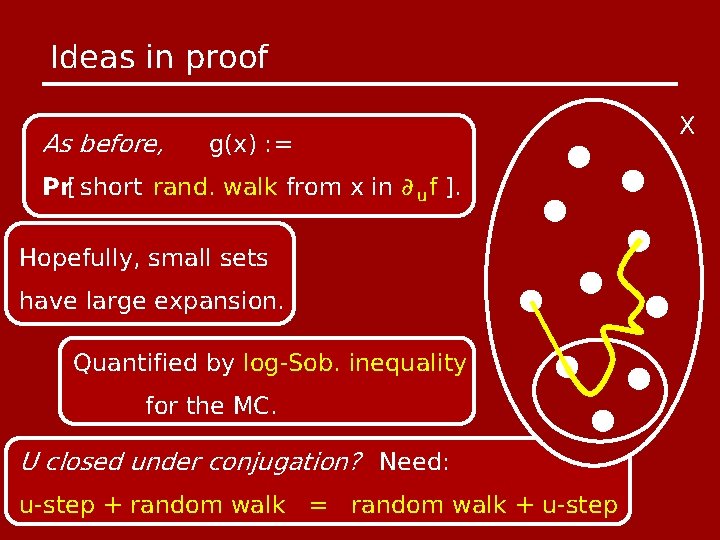
Ideas in proof As before, g(x) : = Pr[ short rand. walk from x in ∂ u f ]. Hopefully, small sets have large expansion. Quantified by log-Sob. inequality for the MC. U closed under conjugation? Need: u-step + random walk = random walk + u-step X

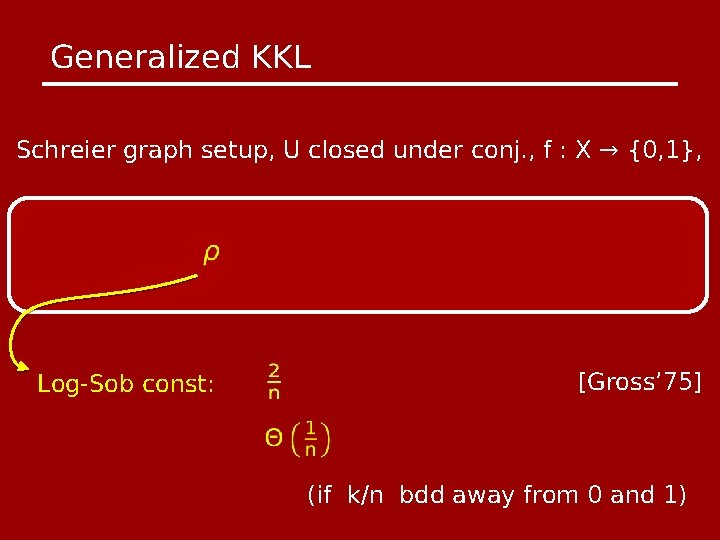
Generalized KKL Schreier graph setup, U closed under conj. , f : X → {0, 1}, Log-Sob const: [Gross’ 75] (if k/n bdd away from 0 and 1)

Generalized KKL Schreier graph setup, U closed under conj. , f : X → {0, 1}, f balanced ⇒ Log-Sob const: [Gross’ 75] (if k/n bdd away from 0 and 1)

Summary: ✔ thm: “KKL on ⇒ ✔ Robust Kruskal-Katona ✔ ⇒ ✔ Net Theorem for mono. fcns ✔

Open problems • Generalize KKL further: weaken “U closed under conjugation” ? • For fun: Our monotone net had size n+3. Could probably make it n+1. Is size n required for an optimal net?