Kirchhoffs laws Outcomes State Kirchhoffs second law and

Kirchhoff’s laws Outcomes: State Kirchhoff’s second law and appreciate that this is a consequence of conservation of energy. Apply Kirchhoff’s first and second laws to circuits. Select and use the equation for the total resistance of two or more resistors in series. Recall and use the equation for the total resistance of two or more resistors in parallel.

Kirchhoff’s first law The German physicist Gustav Kirchhoff established two laws which help us to understand the function of electric circuits. Kirchhoff’s first law states that: The sum of the currents leaving any junction is always equal to the sum of the currents that entered it. This law is based upon the idea of the conservation of charge: no charge can be lost or made in a circuit. I IN Thus the sum of the currents at a junction should be zero. IIN = I 1 + I 2 … + In ΣI = 0 2 of 27 I 1 I 3 I 2 © Boardworks Ltd 2009

The energy in a circuit What happens to the energy supplied to a circuit? Batteries and power supplies supply electrical energy to a circuit. Devices within the circuit transduce this energy: bulbs produce heat and light, resistors produce heat. What is the conservation of energy? Energy cannot be created or destroyed. All of the energy provided by a power supply must be used by the circuit. How does the voltage of a battery relate to the voltage measured across the devices in a circuit? Voltage is the energy transferred to the charge in a circuit. The battery’s voltage is shared between the components, which transduce this energy into different forms. 3 of 27 © Boardworks Ltd 2009

Kirchhoff’s second law is based upon the law of the conservation of energy. It states that: The total voltage across a circuit loop is equal to the sum of the voltage drops across the devices in that loop. Essentially, the energy you put into the circuit equals the energy you get out of each circuit loop. An equation can be produced for each loop in a circuit. For example: VIN = V 1 + V 2 VIN = IR 1 + IR 2 4 of 27 VIN I V 1 V 2 R 1 R 2 © Boardworks Ltd 2009

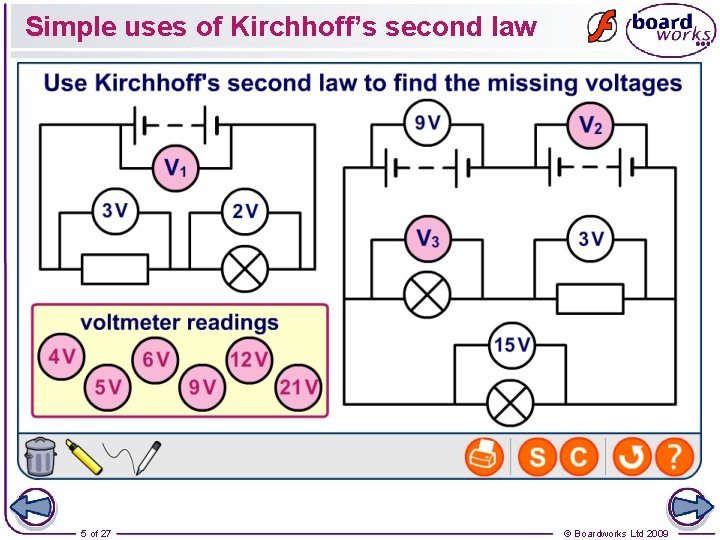
Simple uses of Kirchhoff’s second law 5 of 27 © Boardworks Ltd 2009

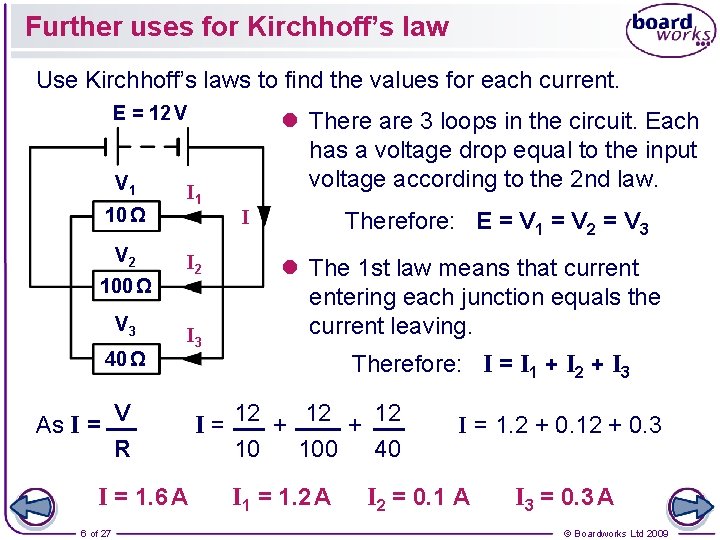
Further uses for Kirchhoff’s law Use Kirchhoff’s laws to find the values for each current. E = 12 V V 1 10 Ω V 2 100 Ω V 3 40 Ω As I = I 1 I 2 I 3 V R I = 1. 6 A 6 of 27 l There are 3 loops in the circuit. Each has a voltage drop equal to the input voltage according to the 2 nd law. I Therefore: E = V 1 = V 2 = V 3 l The 1 st law means that current entering each junction equals the current leaving. Therefore: I = I 1 + I 2 + I 3 I = 12 + 12 10 100 40 I 1 = 1. 2 A I = 1. 2 + 0. 12 + 0. 3 I 2 = 0. 1 A I 3 = 0. 3 A © Boardworks Ltd 2009

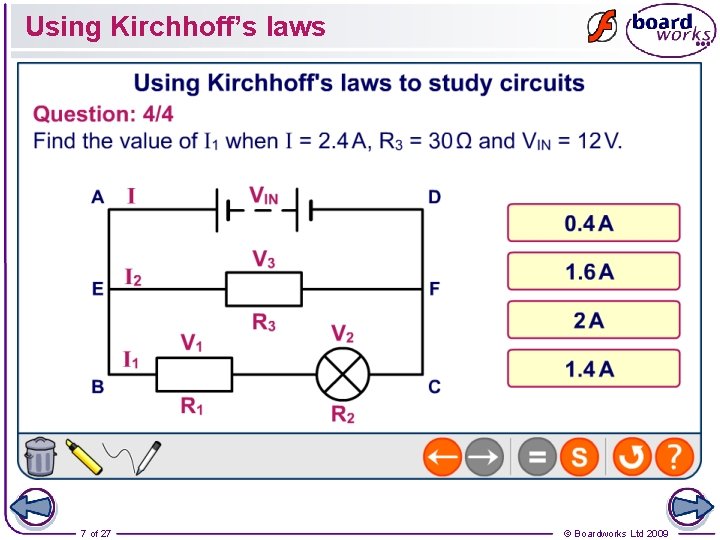
Using Kirchhoff’s laws 7 of 27 © Boardworks Ltd 2009

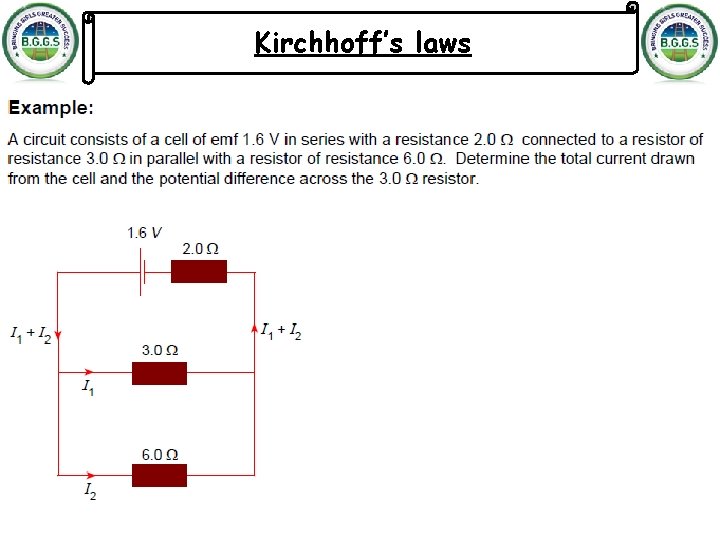
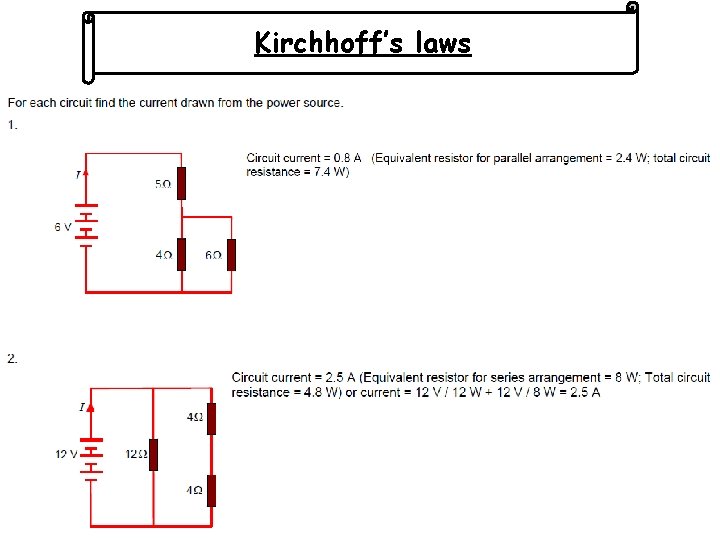
Kirchhoff’s laws

Kirchhoff’s laws

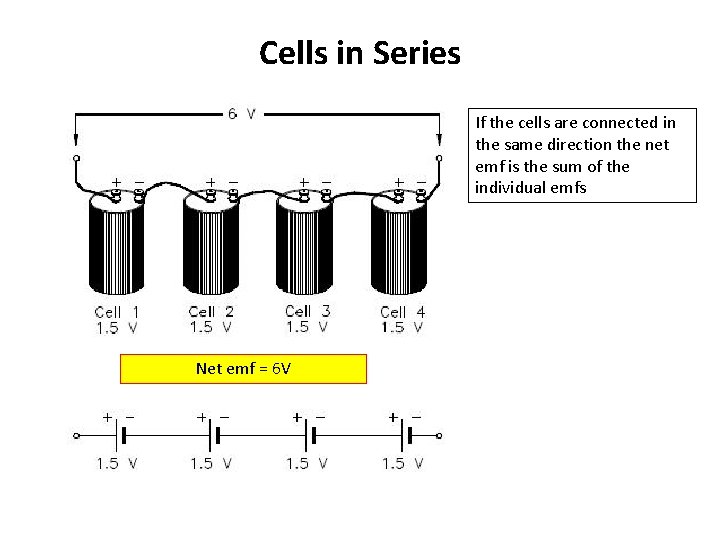
Cells in Series If the cells are connected in the same direction the net emf is the sum of the individual emfs Net emf = 6 V

Cells in Series continued If the cells are connected in opposite directions then net emf is the difference between the emfs, in this case the net emf = 3 V in the direction of the 5 V emf. 2 V 5 V Note: the total internal resistance of the cells in series is the sum of the individual internal resistance of the cells. ( since all the internal resistance are in series) See worked example on page 67

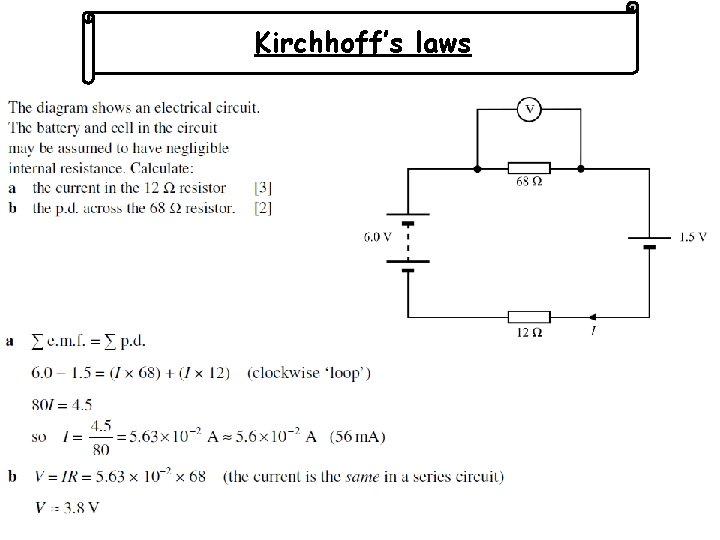
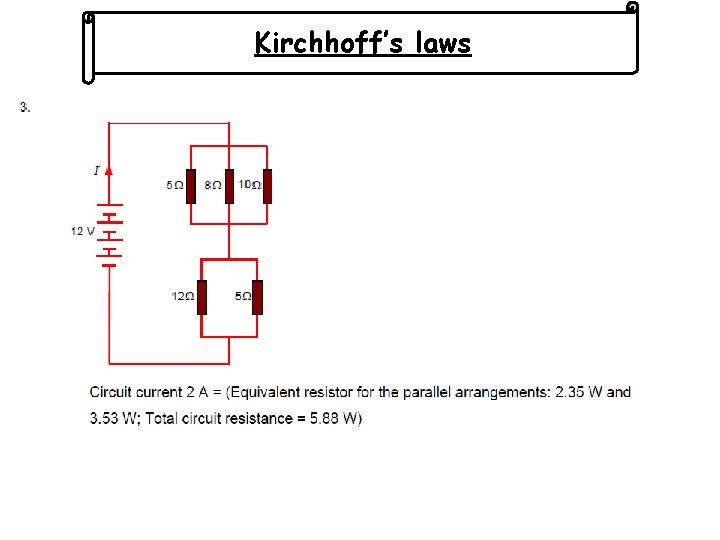
Kirchhoff’s laws

Kirchhoff’s laws

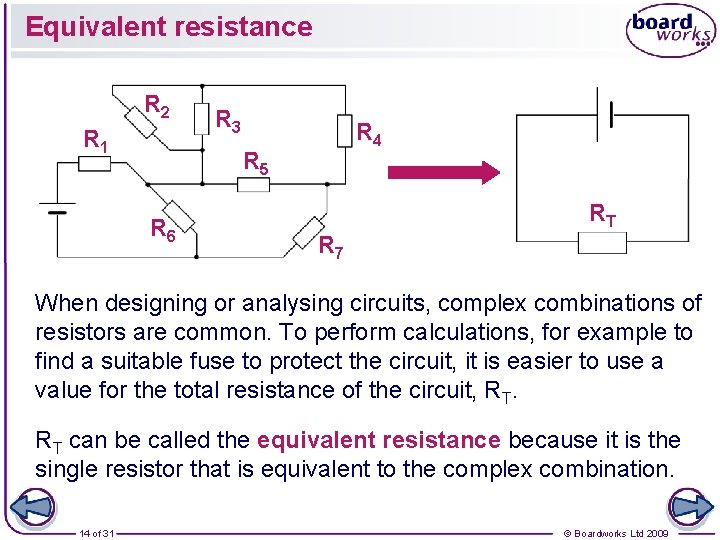
Equivalent resistance R 2 R 1 R 3 R 4 R 5 R 6 RT R 7 When designing or analysing circuits, complex combinations of resistors are common. To perform calculations, for example to find a suitable fuse to protect the circuit, it is easier to use a value for the total resistance of the circuit, RT. RT can be called the equivalent resistance because it is the single resistor that is equivalent to the complex combination. 14 of 31 © Boardworks Ltd 2009

Resistors in series To work out the equivalent resistance of resistors in series, the resistor values can just be added together: 10 Ω 20 Ω 15 Ω equivalent resistance = 10 + 20 + 15 = 45 Ω In general for a number of resistors, n: RT = R 1 + R 2 + … + R n 15 of 31 © Boardworks Ltd 2009

Resistors in Series • In Series, the resistances of the individual components add up, as expected • A few lessons ago we learned that the longer a resistor, the larger its resistance • This is an example of that effect

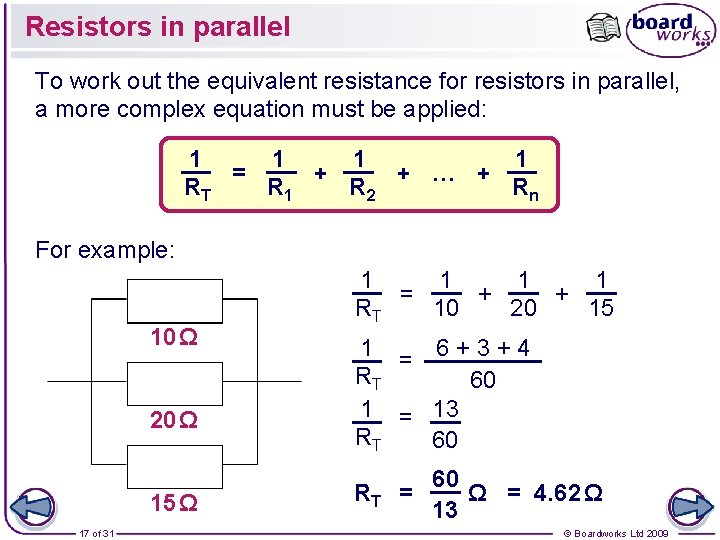
Resistors in parallel To work out the equivalent resistance for resistors in parallel, a more complex equation must be applied: 1 1 = + + … + RT R 1 R 2 Rn For example: 10 Ω 20 Ω 15 Ω 17 of 31 1 1 = + + RT 10 20 15 1 = 6+3+4 RT 60 1 = 13 RT 60 = Ω = 4. 62 Ω 13 © Boardworks Ltd 2009

Resistors in Parallel • In Parallel, adding more resistors reduces the total Resistance • A few lessons ago we learned that the thicker a resistor, the smaller its resistance • This is an example of that effect – two identical resistors in parallel is just like using one resistor that’s twice as wide! So the resistance is halved R 1 R 2 R

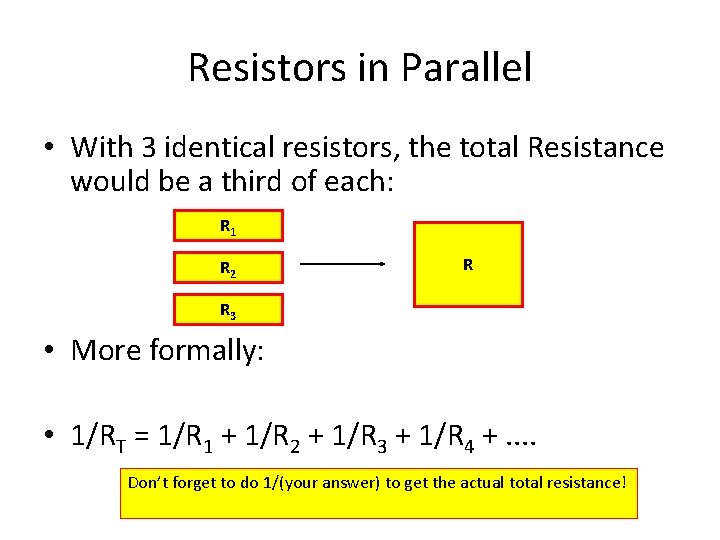
Resistors in Parallel • With 3 identical resistors, the total Resistance would be a third of each: R 1 R 2 R R 3 • More formally: • 1/RT = 1/R 1 + 1/R 2 + 1/R 3 + 1/R 4 +. . Don’t forget to do 1/(your answer) to get the actual total resistance!

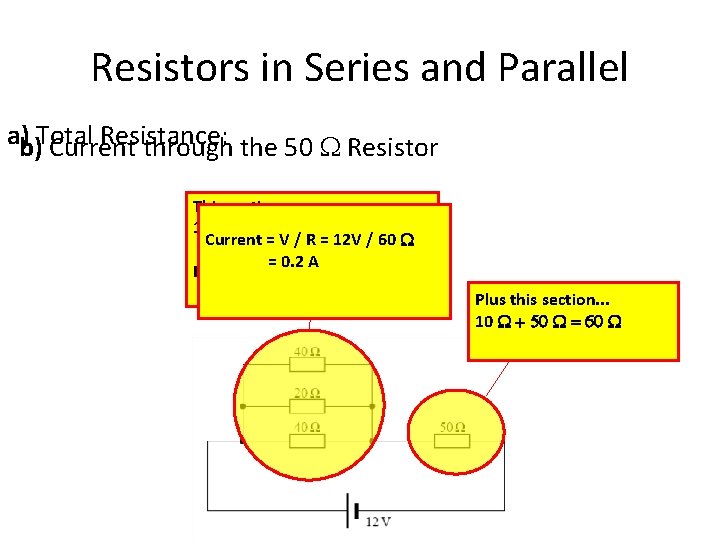
Resistors in Series and Parallel 1 A battery of e. m. f. 12 V and negligible internal resistance is connected to a resistor network as shown in the circuit diagram. (a) Calculate the total resistance of the circuit. (3 marks) (b) Calculate the current through the 50 Ω resistor. (1 mark)

Resistors in Series and Parallel a)b)Total Resistance: Current through the 50 W Resistor This section: 1/RT = 1/40 + 1/20 + 1/40 Current = V / R = 12 V / 60 W = 0. 1 = 0. 2 A RT = 10 W Plus this section. . . 10 W + 50 W = 60 W

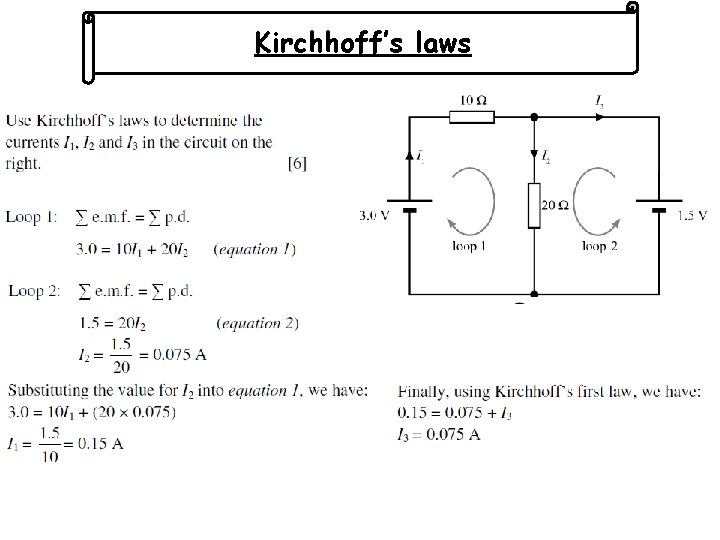
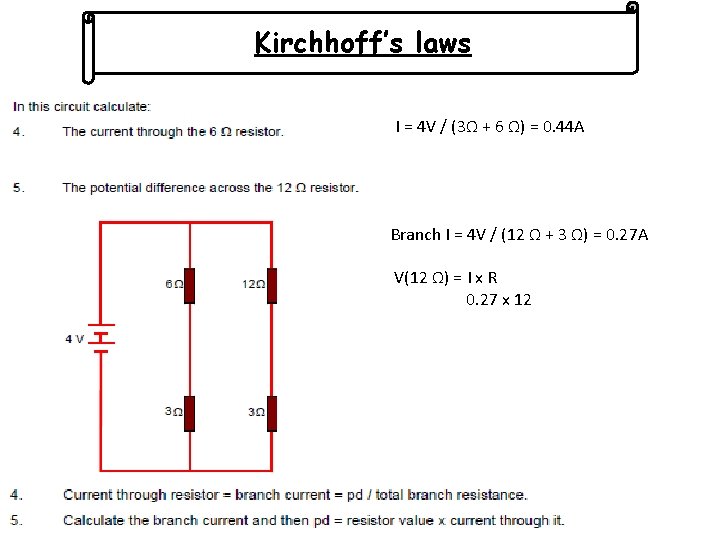
Kirchhoff’s laws

Kirchhoff’s laws

Kirchhoff’s laws I = 4 V / (3Ω + 6 Ω) = 0. 44 A Branch I = 4 V / (12 Ω + 3 Ω) = 0. 27 A V(12 Ω) = I x R 0. 27 x 12