KINETICS AP CHEMISTRY CHAPTER 12 Although we can

KINETICS AP CHEMISTRY CHAPTER 12 Although we can know a lot of things about a chemical reaction, including the reactants and expected products, the stoichiometry and the energy, we must understand the rate of the reaction to truly grasp what is occurring. Although graphite can be compressed into a diamond, the reaction is so slow that we cannot view this in our lifetime. Therefore, we must choose to examine only those reactions that occur at a reasonable rate.

Chemical Kinetics ◦ Thermodynamics tells us if a reaction can occur ◦ Kinetics tells us how quickly the reaction occurs ◦ some reactions that are thermodynamically feasible are kinetically so slow as to be imperceptible 2

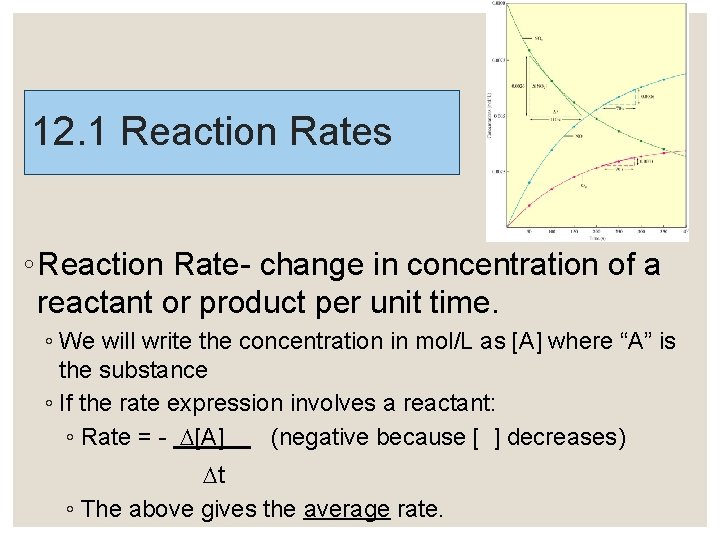
12. 1 Reaction Rates ◦ Reaction Rate- change in concentration of a reactant or product per unit time. ◦ We will write the concentration in mol/L as [A] where “A” is the substance ◦ If the rate expression involves a reactant: ◦ Rate = - [A] (negative because [ ] decreases) t ◦ The above gives the average rate.

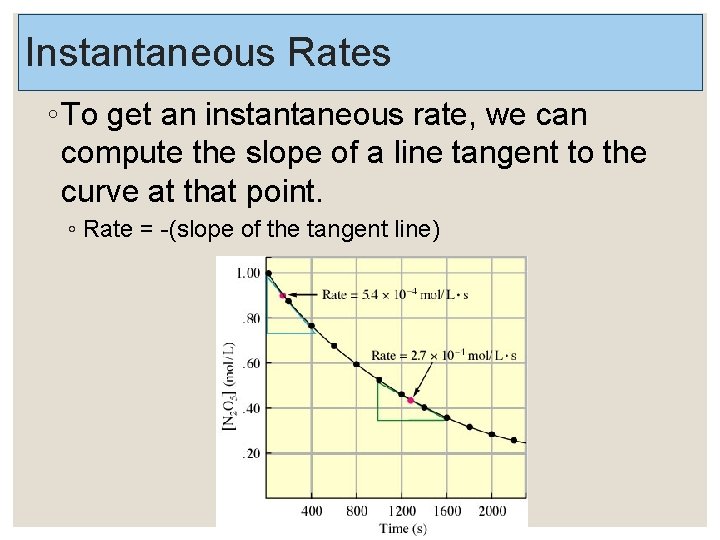
Instantaneous Rates ◦ To get an instantaneous rate, we can compute the slope of a line tangent to the curve at that point. ◦ Rate = -(slope of the tangent line)

We Use “Initial Rates” ◦ The rate of a reaction is not constant but changes with time because concentrations change with time. ◦ We will only work with reaction rates that are “initial rates” (reverse reaction is negligible)

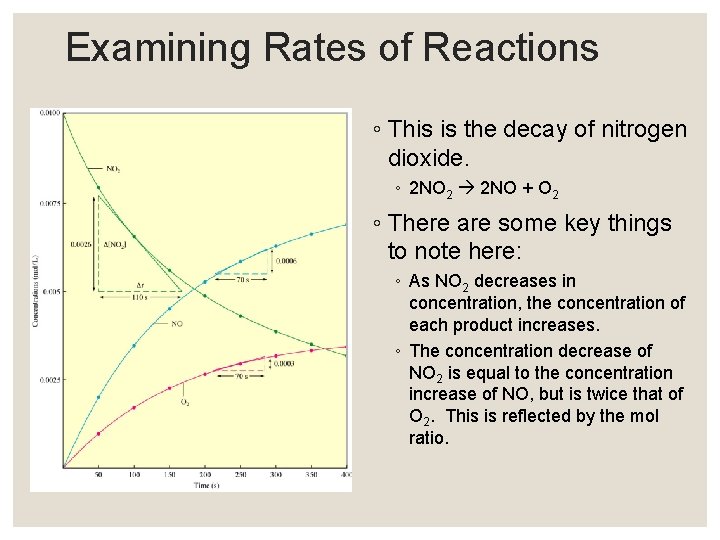
Examining Rates of Reactions ◦ This is the decay of nitrogen dioxide. ◦ 2 NO 2 2 NO + O 2 ◦ There are some key things to note here: ◦ As NO 2 decreases in concentration, the concentration of each product increases. ◦ The concentration decrease of NO 2 is equal to the concentration increase of NO, but is twice that of O 2. This is reflected by the mol ratio.

12. 2 Rate Laws: An Introduction ◦ Rate laws can express how quickly a reactant is consumed or the rate at which a product is produced. In this chapter, however, we will focus on the consumption of reactants. ◦ We will make the assumption that only the forward reaction is occurring; this means that calculations of the reverse reaction do not have to be considered here.

12. 2 Rate Laws: An Introduction ◦ Differential Rate Law or Rate Equation- a rate law that expresses how the rate depends on concentration. ◦ For the reaction a. A + b. B + … g. G + h. H +… ◦ Rate = k[A]m[B]n… ◦ [A] & [B] represent molarities

Rate = k[A]m[B]n ◦ The exponents are positive or negative, integers or fractions. ◦ Usually positive integers (small whole numbers) ◦ k = rate constant ◦ The value of k depends on the type of reaction, temperature and presence of a catalyst ◦ The faster the reaction, the larger the k value

The Order of Reaction ◦ The exponents determine the order of the reactants. The sum of the exponents is the order of the reaction. ◦ R = k[A][B]2 is first order in A, second order in B and third order overall. ◦ The units of k can be calculated by reaction orders and units of concentration and rate.

Finding Units for the Rate Constant ◦ For example, if rate is in mol/L. s in the above rate law, we can find the units for k as follows:

The “shortcut” to determining units of k is as follows: k = Lx/molx. time. ◦ The value of x will be one less than the order of the reaction. ◦ If the reaction is 3 rd order, k = L 2/mol 2. time. ◦ If the reaction is 2 nd order, k = L/mol. time ◦ If the reaction is 1 st order, k = 1/time

12. 3 Determining the Form of the Rate Law ◦ Determining Differential Rate Laws from Experimental Data ◦ If doubling the initial [ ] of a reactant causes the initial rate to double, the reaction is first order in that reactant. ◦ If doubling the initial [ ] of a reactant causes the initial rate to quadruple, the reaction is second order in that reactant. ◦ If doubling the initial [ ] of a reactant causes the initial rate to increase 8 times, the reaction is third order in that reactant. ◦ If doubling the initial [ ] of a reactant does not change the initial rate, the reaction is zero order in that reactant and that reactant is removed from the rate law.

Ex. 2 A + B 2 C [A] 0. 40 0. 80 [B] 0. 20 0. 40 Rate 0. 10 0. 20 0. 80 nd 2 • The reaction is ____ order in terms of A. 1 st • The reaction is ____ order in terms of B. Rate = k[A]2[B] • The rate law is __________. 3 rd order overall. • The reaction is ____

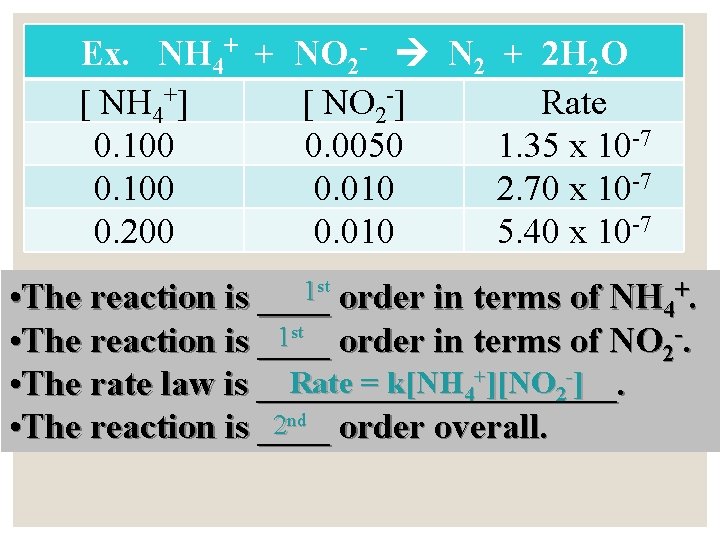
Ex. NH 4+ + NO 2 - N 2 + 2 H 2 O [ NH 4+] [ NO 2 -] Rate 0. 100 0. 0050 1. 35 x 10 -7 0. 100 0. 010 2. 70 x 10 -7 0. 200 0. 010 5. 40 x 10 -7 st 1 • The reaction is ____ order in terms of NH +. 4 NO 2 -. 1 st order in terms of • The reaction is ____ Rate = k[NH 4+][NO 2 -] • The rate law is __________. 2 nd order overall. • The reaction is ____

Ex. A B [A] Rate 0. 050 3. 00 x 10 -4 0. 100 1. 20 x 10 -3 0. 200 4. 80 x 10 -3 x k[A] Rate = k[A]2

[ A] 0. 100 0. 200 0. 400 Ex. A + B C [ B] Rate 0. 200 1. 00 x 10 -5 0. 400 2. 00 x 10 -5 Rate = k[A]x[B]y Rate = k[A]0[B]y Rate = k [B]

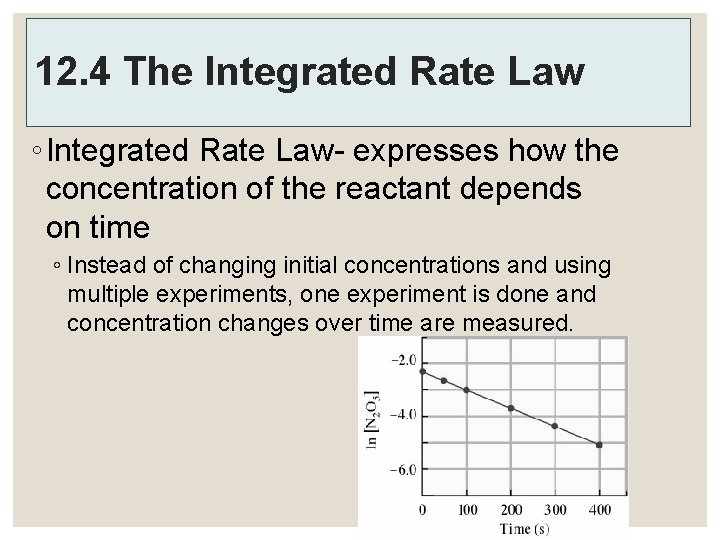
12. 4 The Integrated Rate Law ◦ Integrated Rate Law- expresses how the concentration of the reactant depends on time ◦ Instead of changing initial concentrations and using multiple experiments, one experiment is done and concentration changes over time are measured.

A Note… ◦ The rate law we choose to determine by experiment often depends on what types of data are easiest to collect. If we can conveniently measure how the rate changes as the concentrations are changed, we can readily determine the differential rate law. On the other hand, if it is more convenient to measure eth concentration as a function of time, we can determine the form of the integrated rate law.

1 st order integrated rate law ln [A]0 = kt [A]t “Naughty Katy”

A plot of ln[A] vs t always gives a straight line for a 1 st order reaction. The slope = -k.

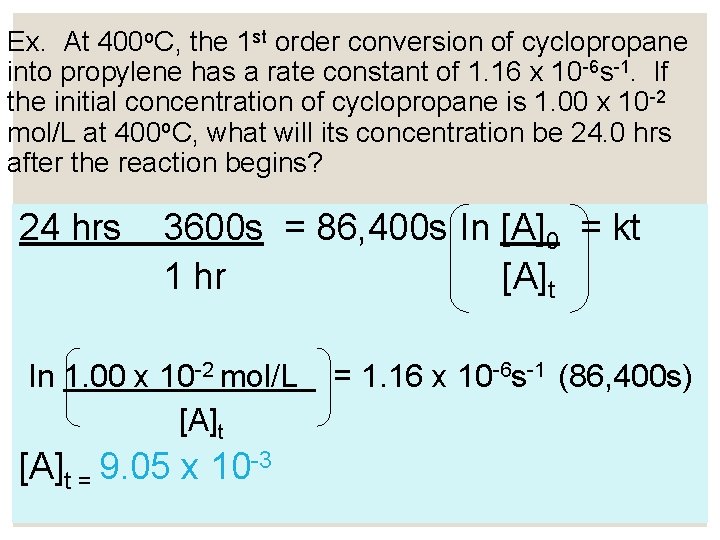
Ex. At 400 o. C, the 1 st order conversion of cyclopropane into propylene has a rate constant of 1. 16 x 10 -6 s-1. If the initial concentration of cyclopropane is 1. 00 x 10 -2 mol/L at 400 o. C, what will its concentration be 24. 0 hrs after the reaction begins? 24 hrs 3600 s = 86, 400 s ln [A]0 = kt 1 hr [A]t ln 1. 00 x 10 -2 mol/L [A]t = 9. 05 x 10 -3 = 1. 16 x 10 -6 s-1 (86, 400 s)

21. 2 The Kinetics of Radioactive Decay ◦ Every radioactive sample has a decay rate, or amount of particles that will decay over time. ◦ This is a first-order process ◦ This a derivative of the “naughty katy” equation ◦ Rate = -(ΔN/Δt) = k. N

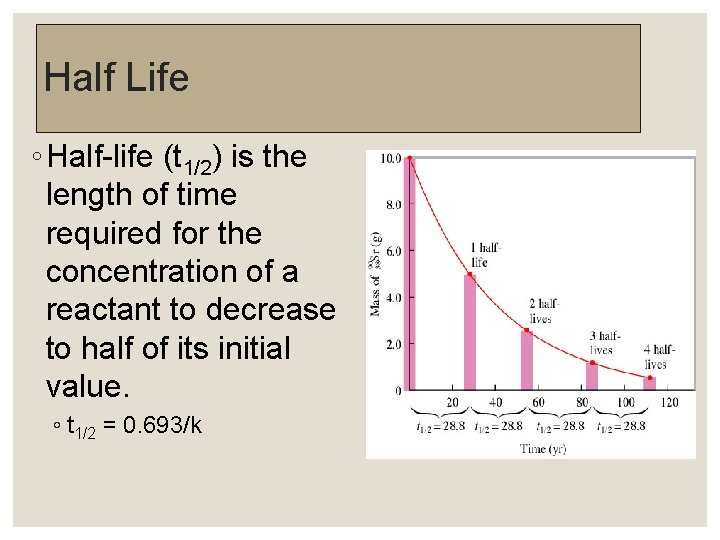
Half Life ◦ Half-life (t 1/2) is the length of time required for the concentration of a reactant to decrease to half of its initial value. ◦ t 1/2 = 0. 693/k

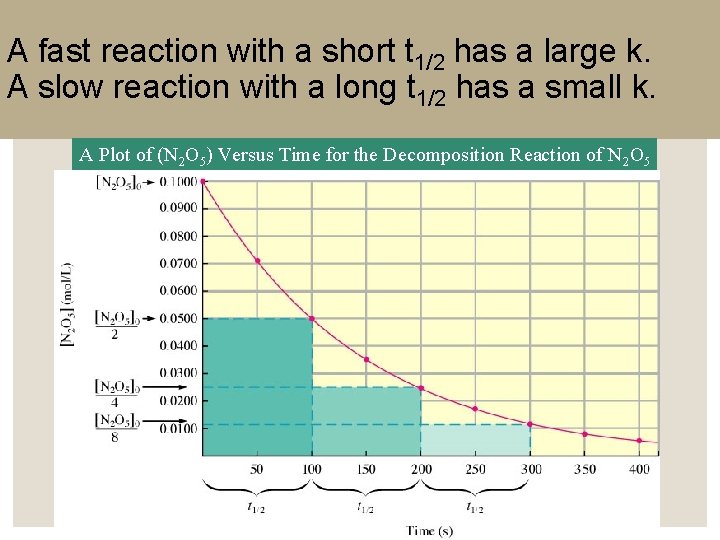
A fast reaction with a short t 1/2 has a large k. A slow reaction with a long t 1/2 has a small k. A Plot of (N 2 O 5) Versus Time for the Decomposition Reaction of N 2 O 5

Example: The decomposition of SO 2 Cl and Cl 2 is a first order reaction with k = 2. 2 x 10 -5 s-1 at 320 o. C. Determine the half-life of this reaction. t 1/2 = 0. 693/k t 1/2 = 0. 693/(2. 2 x 10 -5 s-1) t 1/2 = 31500 s or 525 min or 8. 75 hours

Example: The decomposition of N 2 O 5 dissolved in CCl 4 is a first order reaction. The chemical change is: 2 N 2 O 5 4 NO 2 + O 2 At 45 o. C the reaction was begun with an initial N 2 O 5 concentration of 1. 00 mol/L. After 3. 00 hours the N 2 O 5 concentration had decreased to 1. 21 x 10 -3 mol/L. What is the half-life of N 2 O 5 expressed in minutes at 45 o. C? ln [A]0 = kt [A]t ln 1. 00 = k(180 min) 1. 21 x 10 -3 k = 0. 0373 min-1 t 1/2 = 0. 693/k t 1/2 = 0. 693/0. 0373 min-1 = 18. 6 min

More Advanced Half-life Problems ◦ Ex. The radioactive decay of thallium-206 to lead-206 has a half-life of 4. 20 min. Starting with 5. 00 x 1022 atoms of thallium-206, calculate the number of such atoms left after 42. 0 min. t 1/2 = 0. 693/k 4. 20 min = 0. 693/k k = 0. 165 min-1 ln(N 0/Nt) = kt ln(5. 00 x 1022/Nt) = 0. 165(42. 0) Nt = 4. 89 x 1019 atoms

A freshly isolated sample of 90 Y was found to have an activity of 9. 8 x 105 disintegrations per minute at 1: 00 PM on December 3, 1995. At 2: 15 PM on December 17, 1995, its activity was redetermined and found to be 2. 6 x 104 disintegrations per minute. Calculate the half-life of 90 Y. time = 14 days, 1 ¼ hours = 337. 25 hours ln(N 0 /Nt) = kt ln (9. 8 x 105/2. 6 x 104) = k(337. 25 hr) k = 0. 011 hr -1 t 1/2 = 0. 693/k t 1/2 = 63 hours t 1/2 = 0. 693/0. 011 hr -1

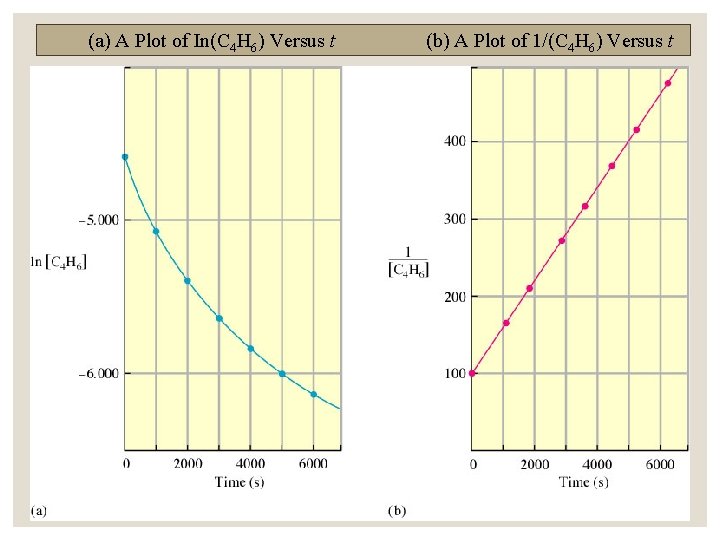
Second order integrated rate law (aka Differential Rate Law) ◦ Rate = k[A]2 1 1 = kt [A]0 A plot of 1/[A]t versus t produces a straight line with slope k.

(a) A Plot of In(C 4 H 6) Versus t (b) A Plot of 1/(C 4 H 6) Versus t

Zero Order Rate Law ◦ Rate = k ◦ [A]t - [A]o = -kt ◦ A plot of [A] versus t produces a straight line with slope -k. A Plot of (A) Versus t for a Zero -Order Reaction

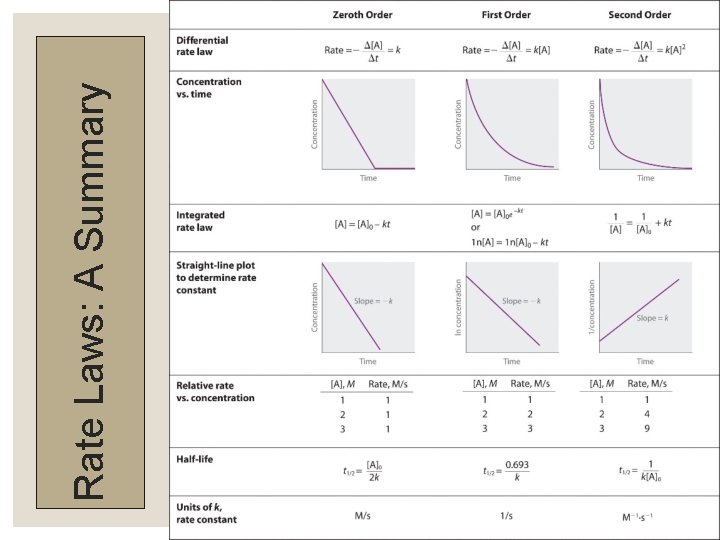
Rate Laws: A Summary

Comparing Class Data Group Concentration % change of mass after 1 min Other variable tested/result

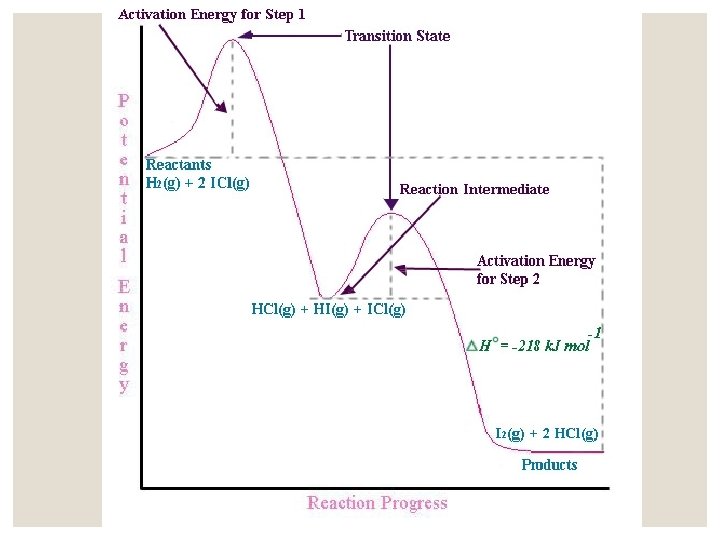
12. 5 Reaction Mechanisms ◦ Reaction mechanisms diagram a series of steps in which a chemical reaction occurs. ◦ Intermediate- a species that is neither a product nor a reactant in the overall equation Is used up in a subsequent step Elementary step- a reaction whose rate law can be written from its molecularity (balanced equation) Molecularity- the number of species that must collide to produce the reaction represented by the elementary step.

Reaction Mechanisms ◦ Unimolecular step- a reaction step involving only one molecule. ◦ Bimolecular step- a reaction step involving the collision of two molecules (Rate law always 2 nd order)

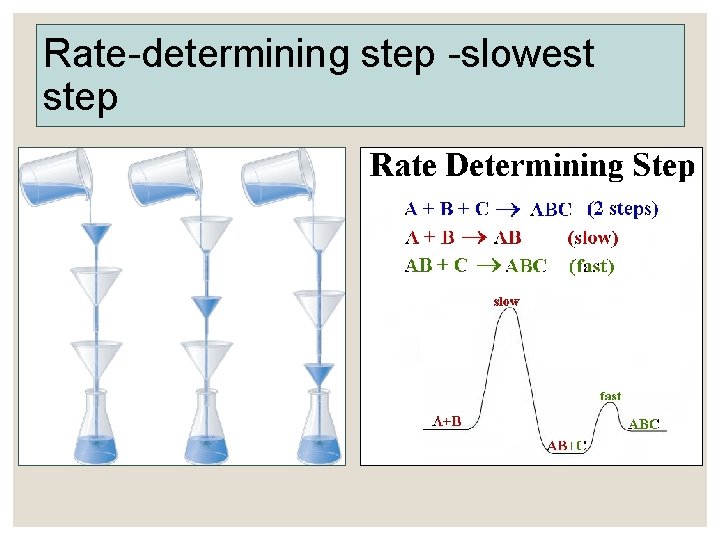
Rate-determining step -slowest step

Elementary Reaction -agrees with the balanced equation • Reaction mechanisms must: • 1. Add up to the overall balanced equation. • 2. Agree with the rate law • We can’t prove a mechanism absolutely. We can only come up with a possible mechanism.

Ex. Elementary Rxn : NO + N 2 O NO 2+ N 2 Rate Law: Rate = k[NO][N 2 O] Ex. The reaction 2 NO 2(g) + F 2(g) 2 NO 2 F is thought to proceed via the following twostep mechanism: NO 2 + F 2 NO 2 F + F slow F + NO 2 F fast Rate law for the reaction: Rate = k [NO 2][F 2]

When an intermediate is a reactant in the ratedetermining step, the derivation of the rate law is more difficult. Ex. NO 2 + CO NO + CO 2 Mechanism: NO 2 + NO 2 k 1 NO 3 + NO fast k-1 NO 3 + CO 2 + NO 2 slow The slow step determines the rate law. Rate law: R = k[NO 3][CO] But, NO 3 was an intermediate. We must come up with something equal to NO 3 to substitute. k[NO 2]2 = k[NO 3][NO] [NO 3] = [NO 2]2 R = k [NO 2]2[CO] [NO]

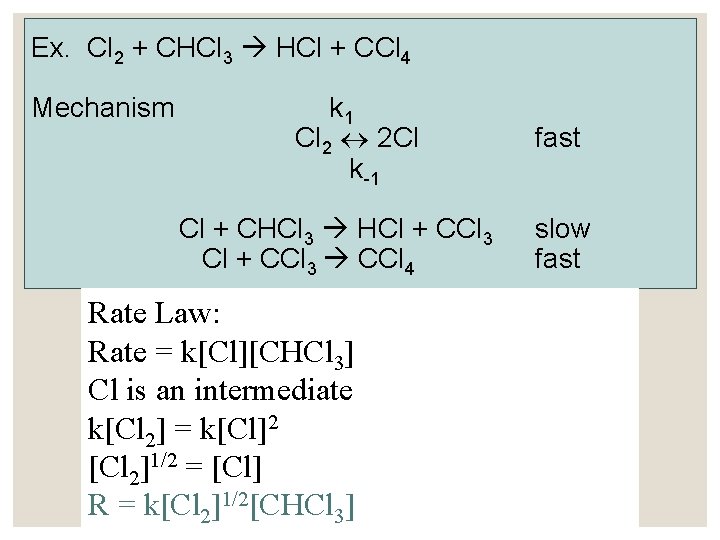
Ex. Cl 2 + CHCl 3 HCl + CCl 4 Mechanism k 1 Cl 2 2 Cl k -1 Cl + CHCl 3 HCl + CCl 3 CCl 4 Rate Law: Rate = k[Cl][CHCl 3] Cl is an intermediate k[Cl 2] = k[Cl]2 [Cl 2]1/2 = [Cl] R = k[Cl 2]1/2[CHCl 3] fast slow fast

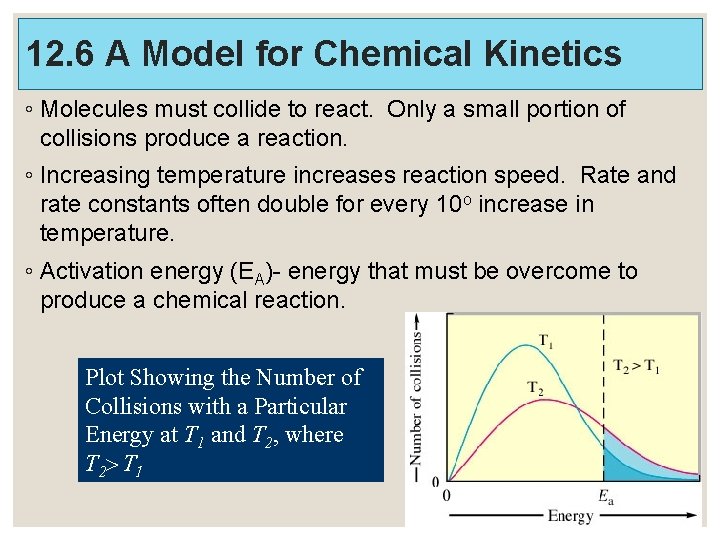
12. 6 A Model for Chemical Kinetics ◦ Molecules must collide to react. Only a small portion of collisions produce a reaction. ◦ Increasing temperature increases reaction speed. Rate and rate constants often double for every 10 o increase in temperature. ◦ Activation energy (EA)- energy that must be overcome to produce a chemical reaction. Plot Showing the Number of Collisions with a Particular Energy at T 1 and T 2, where T 2> T 1

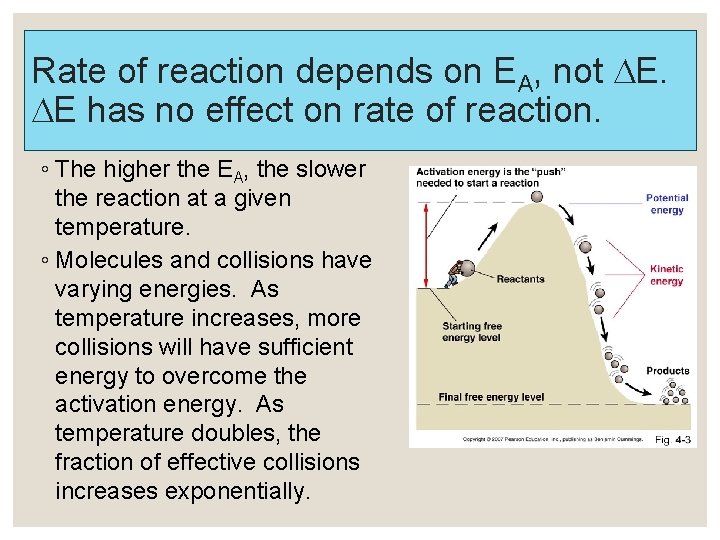
Rate of reaction depends on EA, not E. E has no effect on rate of reaction. ◦ The higher the EA, the slower the reaction at a given temperature. ◦ Molecules and collisions have varying energies. As temperature increases, more collisions will have sufficient energy to overcome the activation energy. As temperature doubles, the fraction of effective collisions increases exponentially.

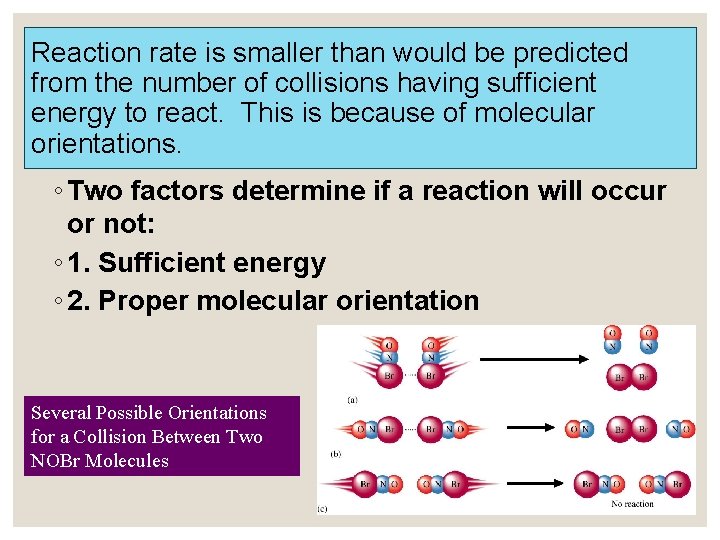
Reaction rate is smaller than would be predicted from the number of collisions having sufficient energy to react. This is because of molecular orientations. ◦ Two factors determine if a reaction will occur or not: ◦ 1. Sufficient energy ◦ 2. Proper molecular orientation Several Possible Orientations for a Collision Between Two NOBr Molecules

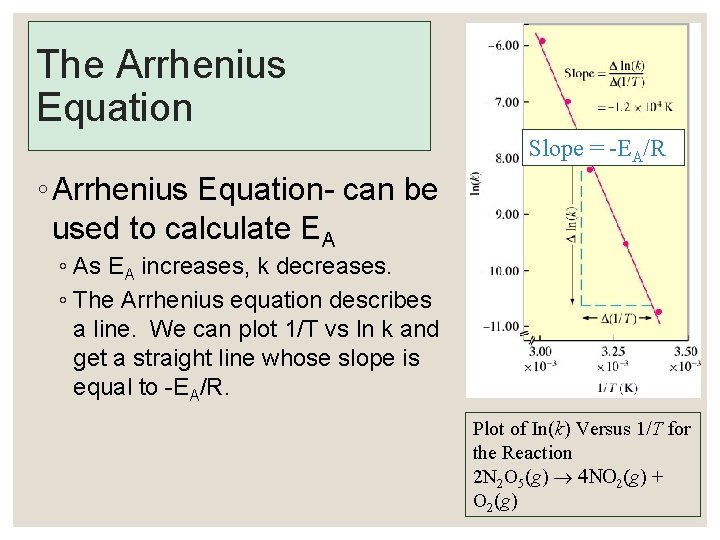
The Arrhenius Equation Slope = -EA/R ◦ Arrhenius Equation- can be used to calculate EA ◦ As EA increases, k decreases. ◦ The Arrhenius equation describes a line. We can plot 1/T vs ln k and get a straight line whose slope is equal to -EA/R. Plot of In(k) Versus 1/T for the Reaction 2 N 2 O 5(g) ® 4 NO 2(g) + O 2(g)

The Arrhenius Equation ln k = ln A - EA RT k = rate constant R = 8. 314 J/K. mol T = Kelvin temperature A = frequency factor (constant as temperature changes) EA = activation energy

The Arrhenius Equation ◦ A variation of the Arrhenius equation can be used to calculate EA or to find k at another temperature if EA is known:

Ex. The rate constant of a first order reaction is 3. 46 x 10 -2 s-1 at 298 K. What is the rate constant at 350 K if the activation energy for the reaction is 50. 2 k. J/mol? ln 3. 46 x 10 -2 s-1 = 50200 J/mol 1 - 1 k 2 8. 314 J/K. mol 350 K 298 K k 2 = 7. 02 x 10 -1 s-1

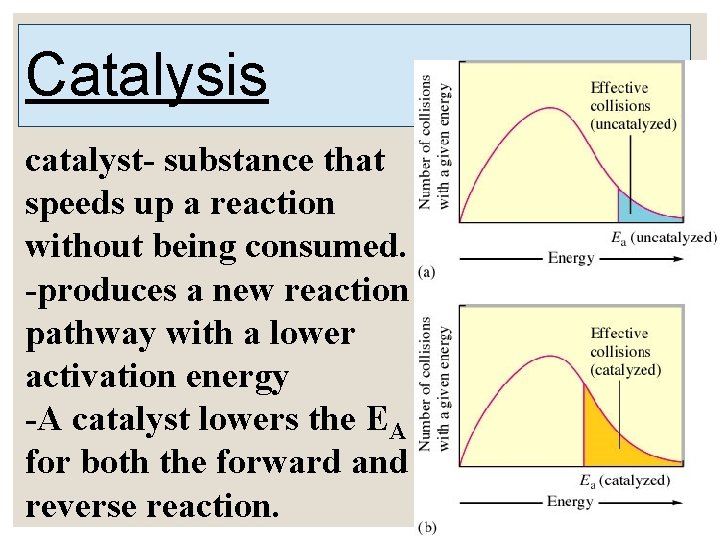
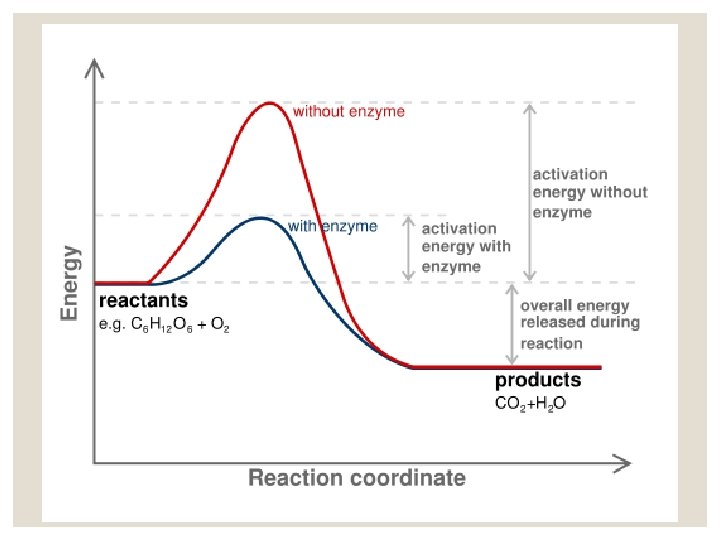
Catalysis catalyst- substance that speeds up a reaction without being consumed. -produces a new reaction pathway with a lower activation energy -A catalyst lowers the EA for both the forward and reverse reaction.

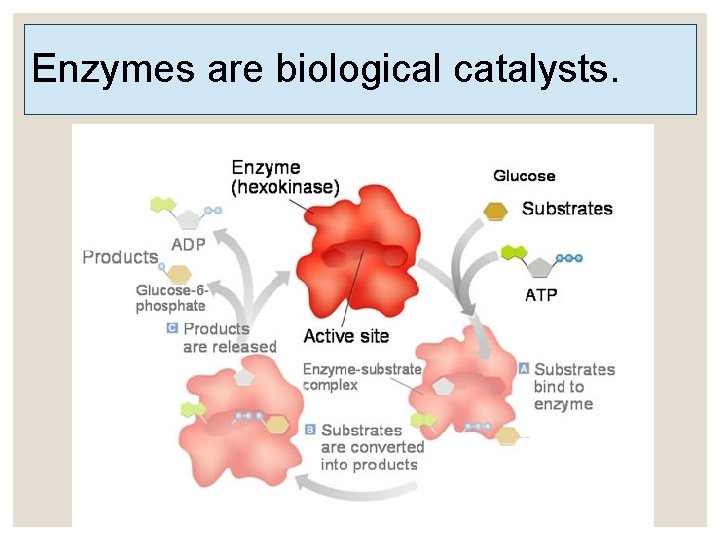
Enzymes are biological catalysts.

Types of Inorganic Catalysts ◦ homogeneous catalyst- present in the same phase as the reacting molecules (usually liquid phase) ◦ heterogeneous catalyst- exists in a different phase ◦ Usually involves gaseous reactants being adsorbed on the surface of a solid catalyst (such as a car’s catalytic converter) ◦ Absorption involves penetration. Heterogeneous Catalysis of the Hydrogenation of Ethylene