Kinetic Theory of Gases I Ideal Gas The

Ideal Gas The number of molecules is large The average separation between molecules is

The Ideal Gas Law in K n: the number of moles in the ideal

Pressure and Temperature Pressure: Results from collisions of molecules on the surface Force Pressure:

Only molecules moving toward the surface hit the surface. Assuming the surface is normal

Momentum in time dt: Force: Pressure: Not all molecules have the same

is the root-mean-square speed Pressure: Average Translational Kinetic Energy:

Pressure: From Temperature: Boltzmann constant: and

Pressure Density x Kinetic Energy Temperature Kinetic Energy

Internal Energy For monatomic gas: the internal energy = sum of the kinetic energy

HRW 16 P (5 th ed. ). Consider a given mass of an ideal

HRW 18 P (5 th ed. ). A sample of an ideal gas is

HRW 30 E (5 th ed. ). (a) Compute the root-mean-square speed of a

HRW 34 E (5 th ed. ). What is the average translational kinetic energy

Mean Free Path Molecules collide elastically with other molecules Mean Free Path l: average

Molar Specific Heat Definition: For constant volume: For constant pressure: The 1 st Law

1 st Law Adiabatic Process (Q=0) Divide by p. V: Ideal Gas Law

Equipartition of Energy The internal energy of non-monatomic molecules includes also vibrational and rotational

Monatomic Gases 3 translational degrees of freedom:

Diatomic Gases 3 translational degrees of freedom 2 rotational degrees of freedom 2 vibrational

HRW 63 P (5 th ed. ). Let 20. 9 J of heat be

HRW 81 P (5 th ed. ). An ideal gas experiences an adiabatic compression

Slides: 31

Download presentation

Kinetic Theory of Gases I

Ideal Gas The number of molecules is large The average separation between molecules is large Molecules moves randomly Molecules obeys Newton’s Law Molecules collide elastically with each other and with the wall Consists of identical molecules

The Ideal Gas Law in K n: the number of moles in the ideal gas total number of molecules Avogadro’s number: the number of atoms, molecules, etc, in a mole of a substance: NA=6. 02 x 1023/mol. R: the Gas Constant: R = 8. 31 J/mol · K

Pressure and Temperature Pressure: Results from collisions of molecules on the surface Force Pressure: Force: Area Rate of momentum given to the surface Momentum: momentum given by each collision times the number of collisions in time dt

Only molecules moving toward the surface hit the surface. Assuming the surface is normal to the x axis, half the molecules of speed vx move toward the surface. Only those close enough to the surface hit it in time dt, those within the distance vxdt The number of collisions hitting an area A in time dt is Average density The momentum given by each collision to the surface

Momentum in time dt: Force: Pressure: Not all molecules have the same

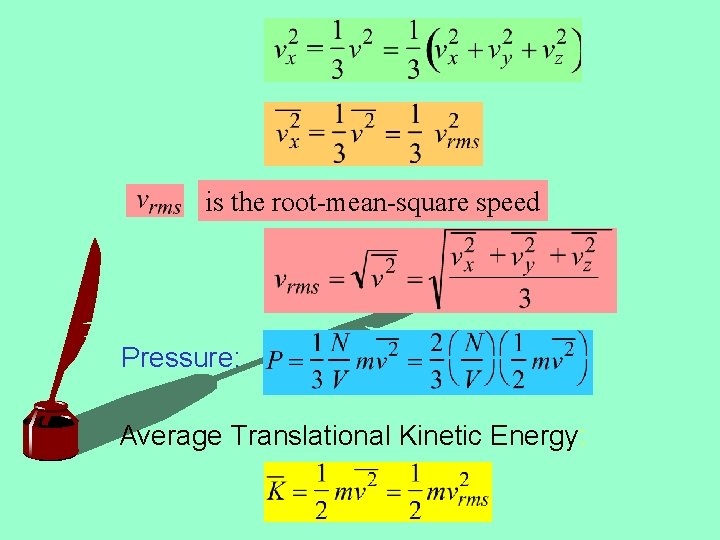
is the root-mean-square speed Pressure: Average Translational Kinetic Energy:

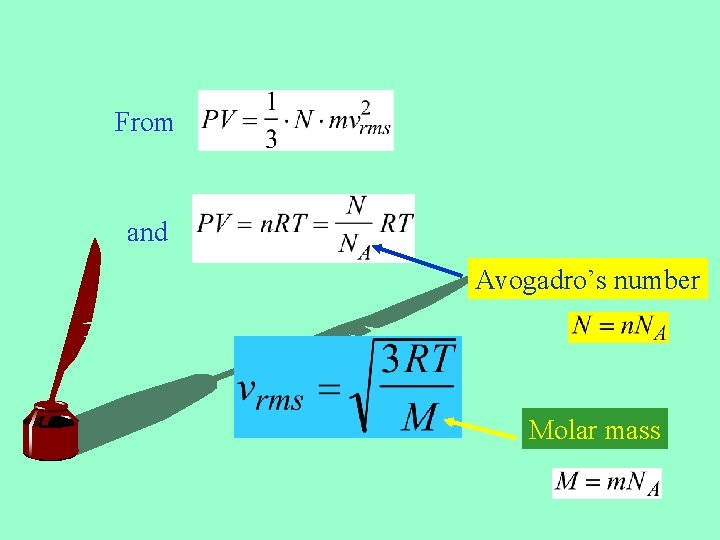
Pressure: From Temperature: Boltzmann constant: and

From and Avogadro’s number Molar mass

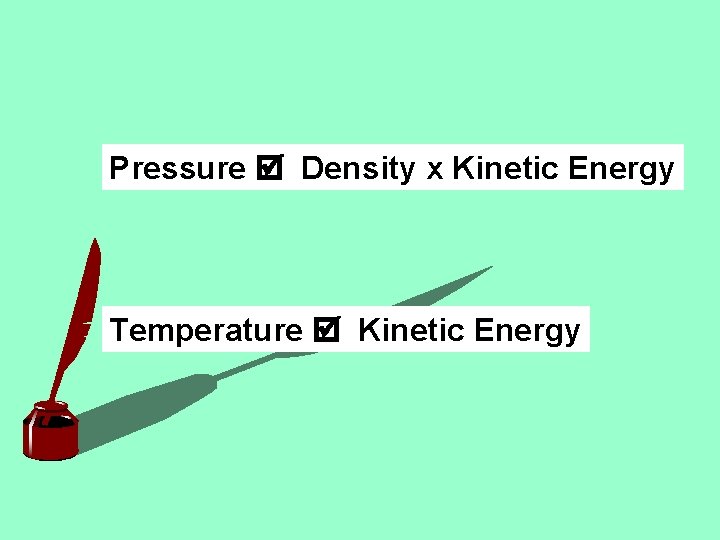
Pressure Density x Kinetic Energy Temperature Kinetic Energy

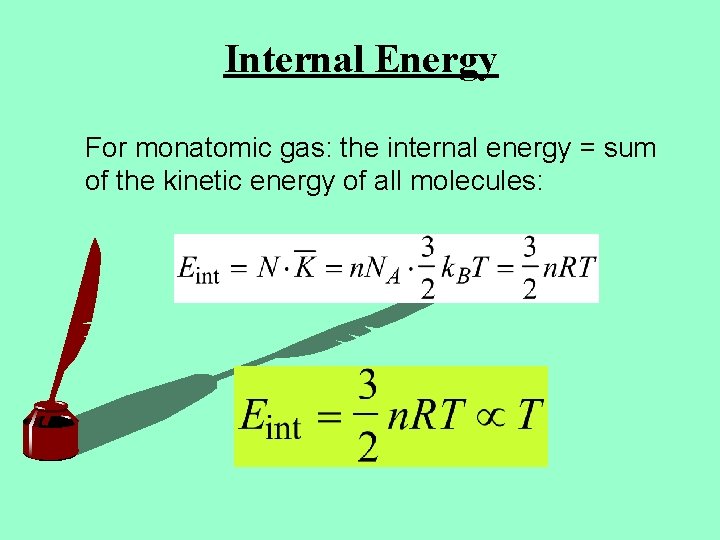
Internal Energy For monatomic gas: the internal energy = sum of the kinetic energy of all molecules:

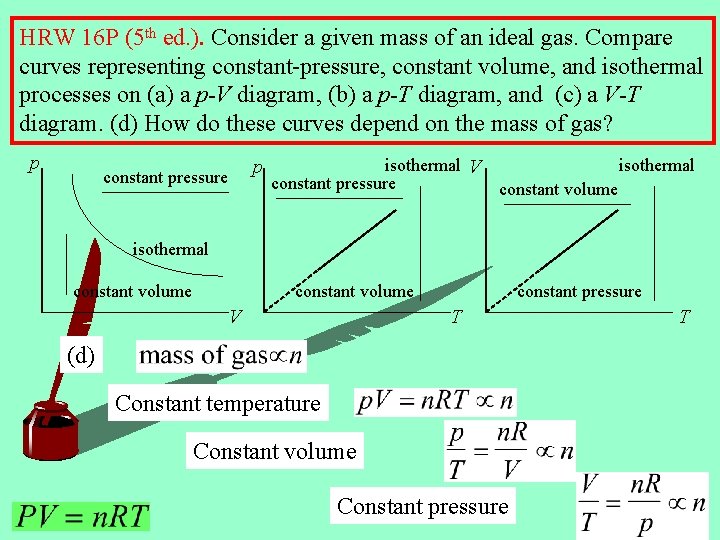
HRW 16 P (5 th ed. ). Consider a given mass of an ideal gas. Compare curves representing constant-pressure, constant volume, and isothermal processes on (a) a p-V diagram, (b) a p-T diagram, and (c) a V-T diagram. (d) How do these curves depend on the mass of gas? p p constant pressure isothermal V isothermal constant pressure constant volume isothermal constant volume V constant pressure T (d) Constant temperature Constant volume Constant pressure T

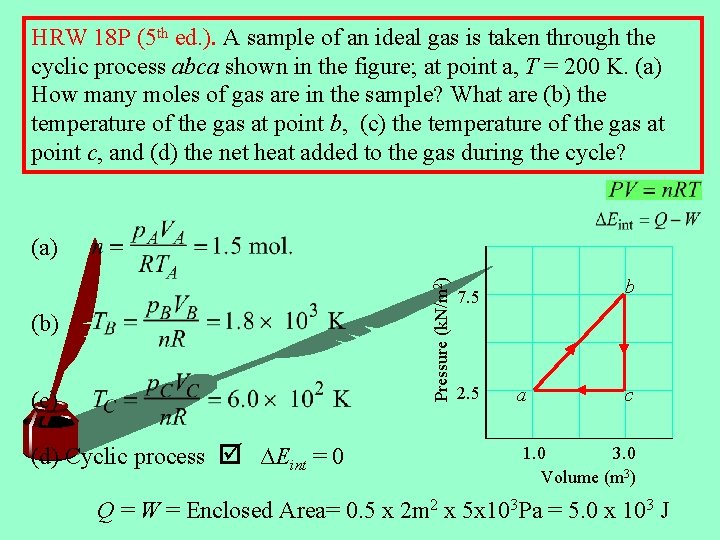
HRW 18 P (5 th ed. ). A sample of an ideal gas is taken through the cyclic process abca shown in the figure; at point a, T = 200 K. (a) How many moles of gas are in the sample? What are (b) the temperature of the gas at point b, (c) the temperature of the gas at point c, and (d) the net heat added to the gas during the cycle? Pressure (k. N/m 2) (a) (b) (c) (d) Cyclic process ∆Eint = 0 b 7. 5 2. 5 a c 1. 0 3. 0 Volume (m 3) Q = W = Enclosed Area= 0. 5 x 2 m 2 x 5 x 103 Pa = 5. 0 x 103 J

HRW 30 E (5 th ed. ). (a) Compute the root-mean-square speed of a nitrogen molecule at 20. 0 ˚C. At what temperatures will the rootmean-square speed be (b) half that value and (c) twice that value? (a) (b) Since for 0. 5 vrms for 2 vrms

HRW 34 E (5 th ed. ). What is the average translational kinetic energy of nitrogen molecules at 1600 K, (a) in joules and (b) in electronvolts? (a) (b) 1 e. V = 1. 60 x 10 -19 J

Kinetic Theory of Gases II

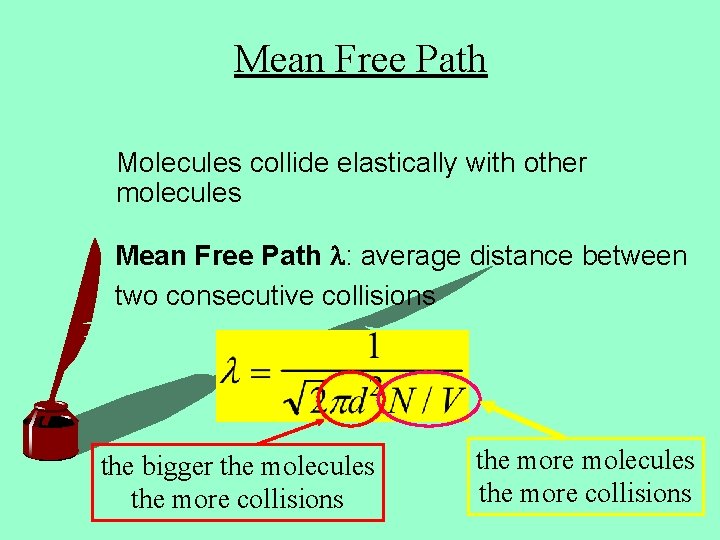
Mean Free Path Molecules collide elastically with other molecules Mean Free Path l: average distance between two consecutive collisions the bigger the molecules the more collisions the more molecules the more collisions

Molar Specific Heat Definition: For constant volume: For constant pressure: The 1 st Law of Thermodynamics: (Monatomic)

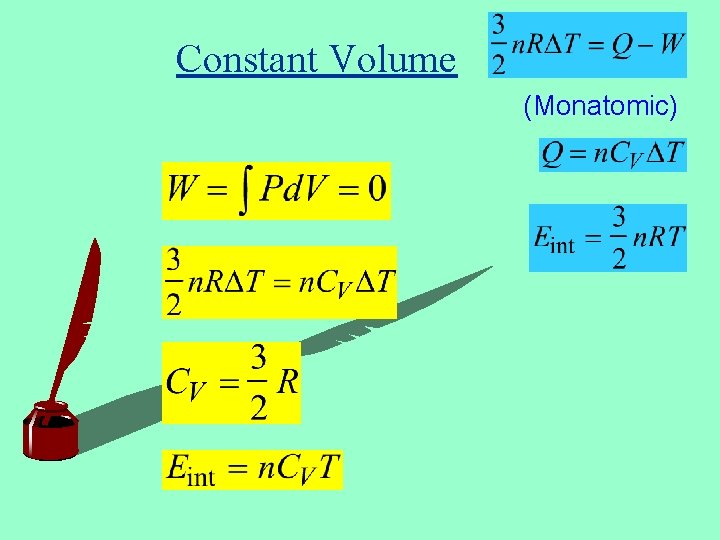
Constant Volume (Monatomic)

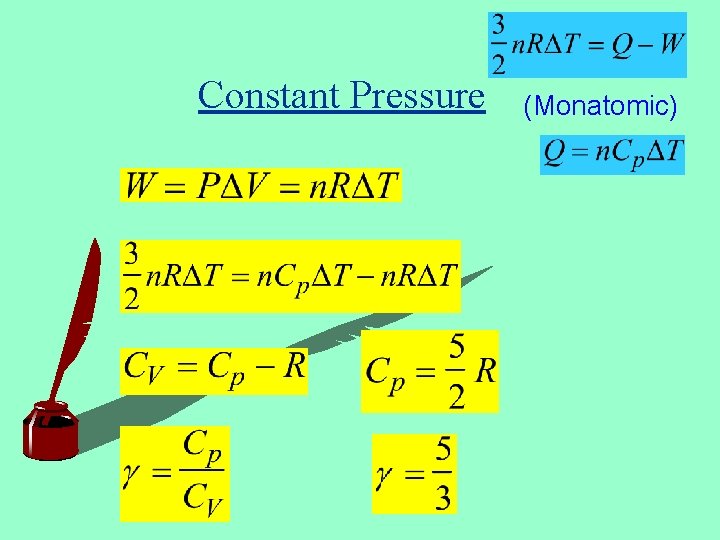
Constant Pressure (Monatomic)

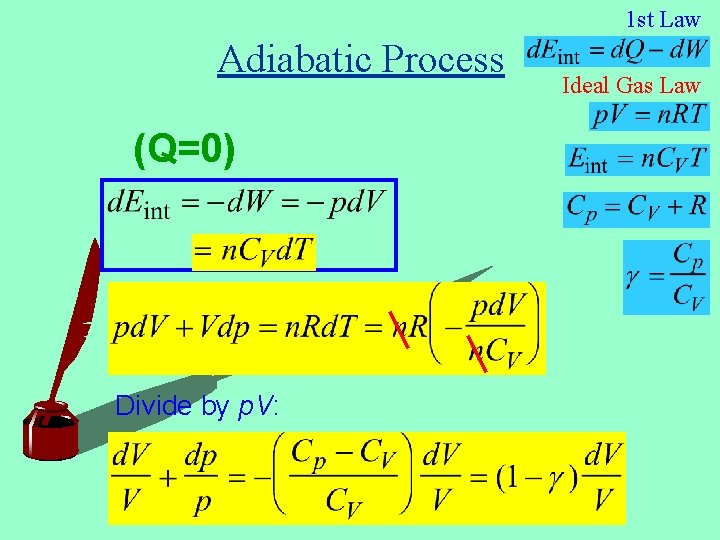
1 st Law Adiabatic Process (Q=0) Divide by p. V: Ideal Gas Law

Ideal Gas Law

Equipartition of Energy The internal energy of non-monatomic molecules includes also vibrational and rotational energies besides the translational energy. Each degree of freedom has associated with it an energy of per molecules.

Monatomic Gases 3 translational degrees of freedom:

Diatomic Gases 3 translational degrees of freedom 2 rotational degrees of freedom 2 vibrational degrees of freedom HOWEVER, different DOFs require different temperatures to excite. At room temperature, only the first two kinds are excited:

HRW 63 P (5 th ed. ). Let 20. 9 J of heat be added to a particular ideal gas. As a result, its volume changes from 50. 0 cm 3 to 100 cm 3 while the pressure remains constant at 1. 00 atm. (a) By how much did the internal energy of the gas change? If the quantity of gas present is 2. 00 x 10 -3 mol, find the molar specific heat at (b) constant pressure and (c) constant volume. (a) Constant pressure: W = p∆V

HRW 81 P (5 th ed. ). An ideal gas experiences an adiabatic compression from p =1. 0 atm, V =1. 0 x 106 L, T = 0. 0 ˚C to p =1. 0 x 105 atm, V =1. 0 x 103 L. (a) Is the gas monatomic, diatomic, or polyatomic? (b) What is its final temperature? (c) How many moles of gas are present? (d) What is the total translational kinetic energy per mole before and after the compression? (e) What is the ratio of the squares of the rms speeds before and after the compression? (a) Adiabatic Monatomic