Kinetic Molecular Theory Postulates of the Kinetic Molecular











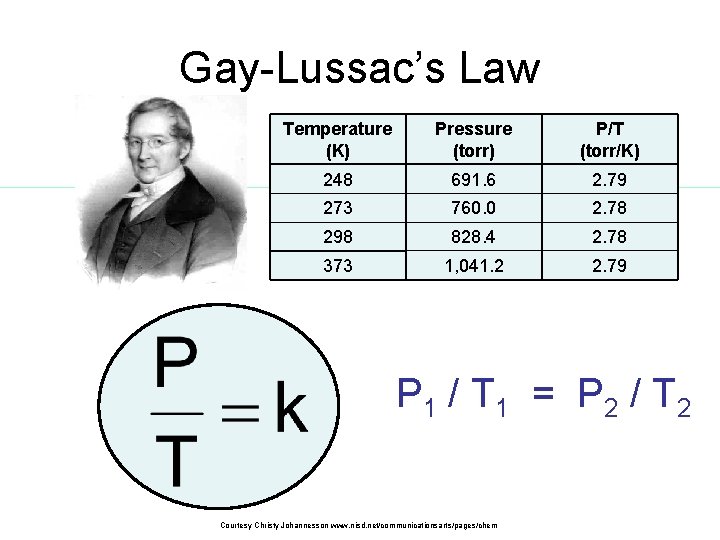


















- Slides: 39

Kinetic Molecular Theory Postulates of the Kinetic Molecular Theory of Gases 1. Gases consist of particles (atoms or molecules) in constant, straight-line motion. 2. Gas particles do not attract or repel each other (no interactions). Particles collide with each other and surfaces elastically. Collisions with walls of container define pressure (P = F/A). 3. Gas particles are small, compared with the distances between them. Hence, the volume (size) of the individual particles can be assumed to be negligible (zero). 4. The average kinetic energy of the gas particles is directly proportional to the Kelvin temperature of the gas

Properties of Gases expand to fill any container. – random motion, no attraction Gases are fluids (like liquids). – particles flow easily Gases have very low densities. – lots of empty space; particles spaced far apart Gases are easily compressible. – empty space reduced to smaller volume Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

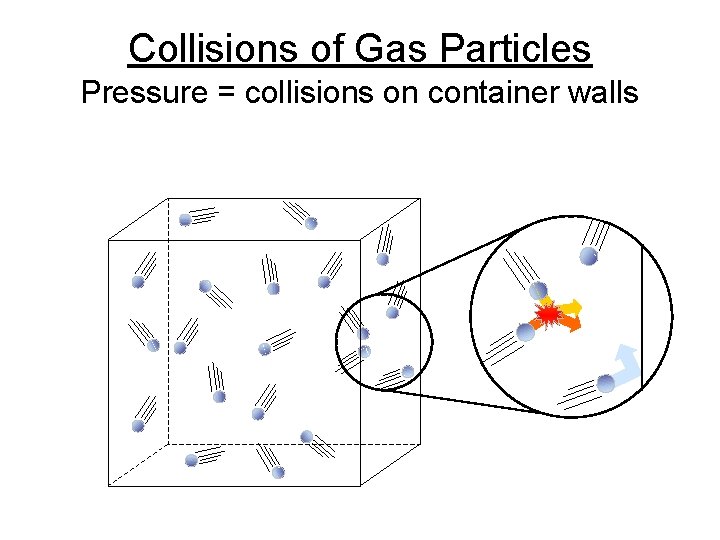
Collisions of Gas Particles Pressure = collisions on container walls

Changing the Size of the Container • In a smaller container - particles have less room to move. • Particles hit the sides of the container more often. • This causes an increase in pressure. • As volume decreases: pressure increases.

Pressure = Force/Area KEY UNITS AT SEA LEVEL (also known as standard pressure) 101. 325 k. Pa (kilopascal) 1 atm 760 mm Hg 760 torr 14. 7 psi Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem Sea level

Barometers Mount Everest Sea level On top of Mount Everest

Temperature Always use temperature in Kelvin when working with gases. Std temperature = 273 K ºF -459 ºC -273 K 0 32 212 0 100 273 373 K = ºC + 273 Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

STP Standard Temperature & Pressure 0°C 1 atm 273 K - OR - 101. 325 k. Pa Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

Boyle’s Law • As the pressure on a gas increases the volume decreases 1 atm 2 atm 4 Liters 2 • Pressure and volume are inversely related

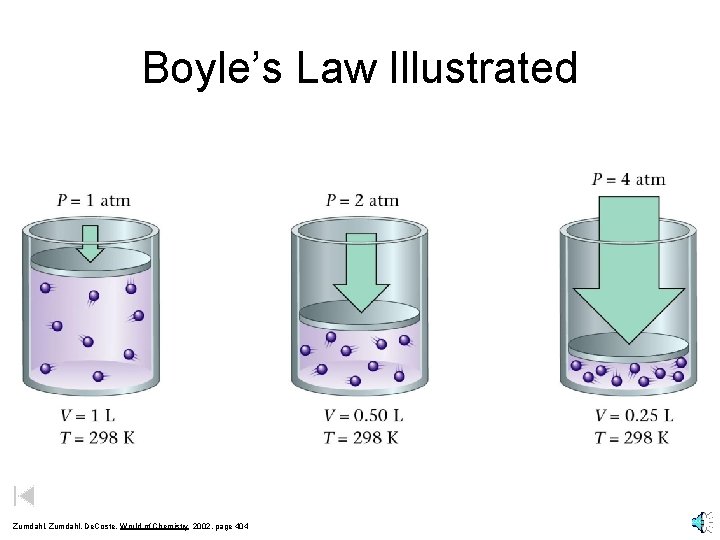
Boyle’s Law Illustrated Zumdahl, De. Coste, World of Chemistry 2002, page 404

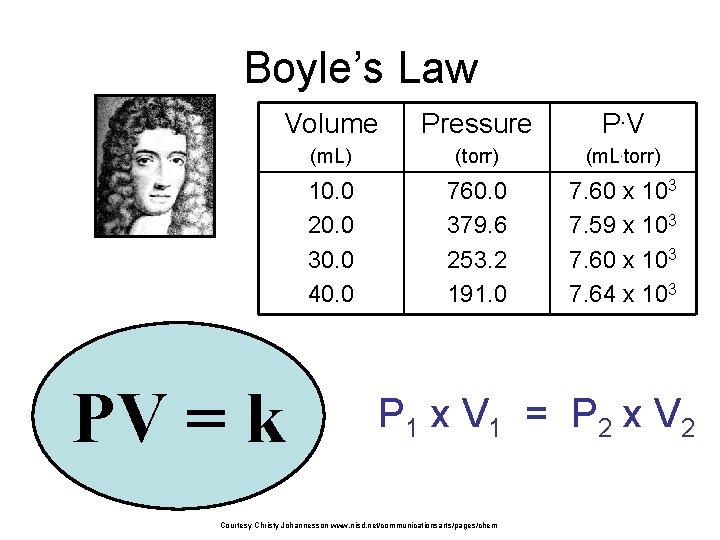
Boyle’s Law Volume b. The Pressure P. V pressure and volume (torr) (m. L. torr) of 10. 0 a gas are 760. 0 inversely 7. 60 x 103 related 20. 0 379. 6 7. 59 x 103 (m. L) • at constant 253. 2 mass & temp 30. 0 7. 60 x 103 40. 0 191. 0 7. 64 x 103 PV = k P 1 x V 1 = P 2 x V 2 Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

Boyle’s Law example A quantity of gas under a pressure of 106. 6 k. Pa has a volume of 380 cm 3. What is the volume of the gas at standard pressure, if the temperature is held constant? P 1 x V 1 = P 2 x V 2 (106. 6 k. Pa) x (380 cm 3) = (101. 3 k. Pa) x (V 2) V 2 = 400 cm 3

Charles’s Law Timberlake, Chemistry 7 th Edition, page 259

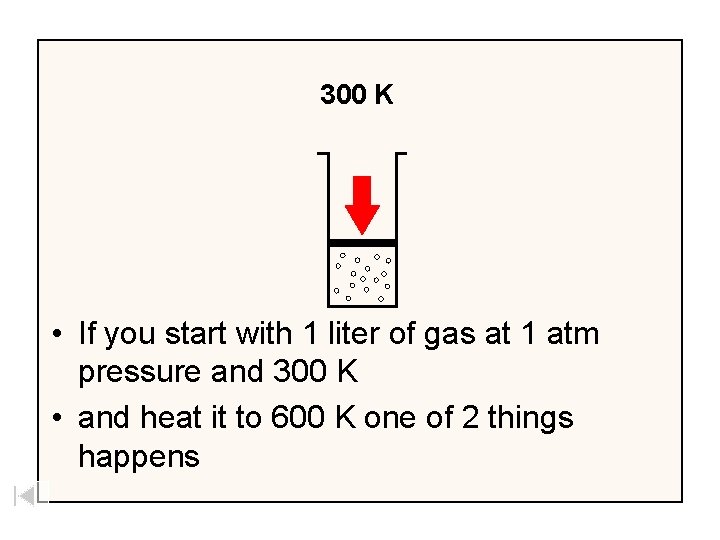
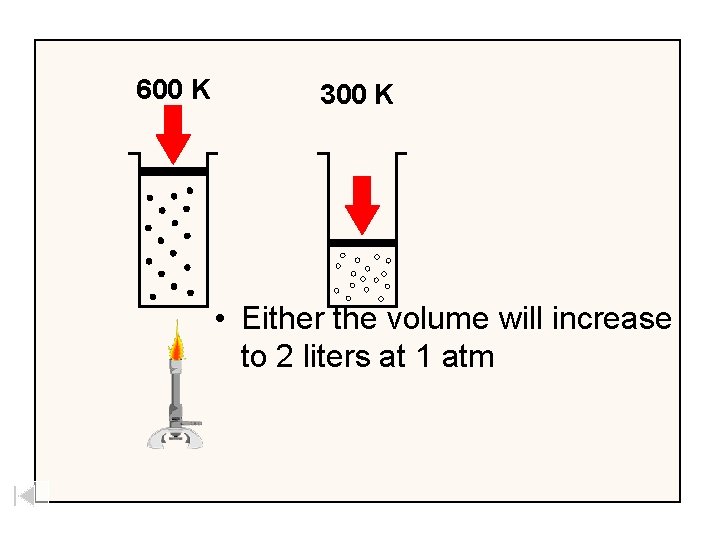
300 K • If you start with 1 liter of gas at 1 atm pressure and 300 K • and heat it to 600 K one of 2 things happens

600 K 300 K • Either the volume will increase to 2 liters at 1 atm

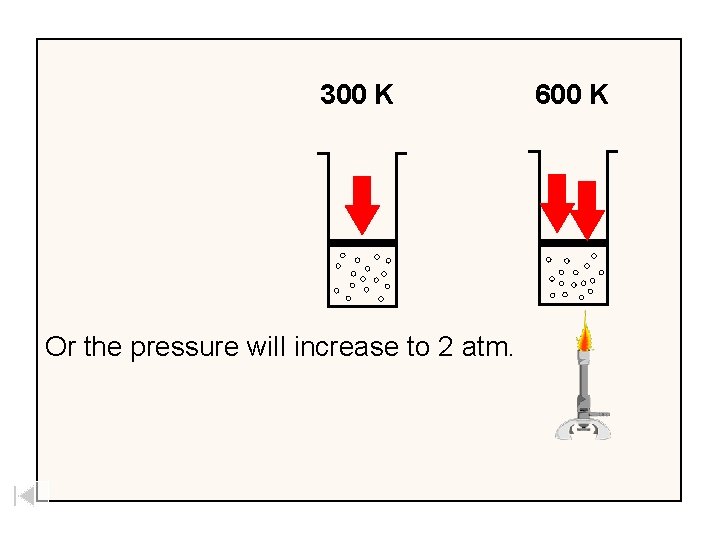
300 K Or the pressure will increase to 2 atm. 600 K

Charles’ Law Volume Temperature V/T The volume and absolute (m. L) (K) (m. L / K) temperature (K) of a gas are 40. 0 273. 2 0. 146 directly related 44. 0 298. 2 0. 148 –at constant mass & pressure 47. 7 323. 2 0. 148 51. 3 348. 2 0. 147 V 1 / T 1 = V 2 / T 2 Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem
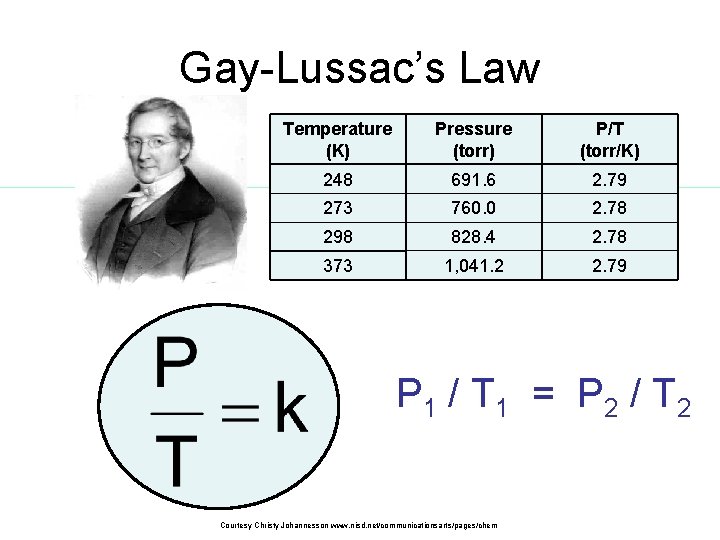
Gay-Lussac’s Law Temperature (K) Pressure (torr) P/T (torr/K) The pressure and absolute 248 691. 6 2. 79 are temperature (K) of a gas 273 760. 0 2. 78 directly related 298 828. 4 2. 78 – at 373 constant 1, 041. 2 mass & volume 2. 79 P 1 / T 1 = P 2 / T 2 Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

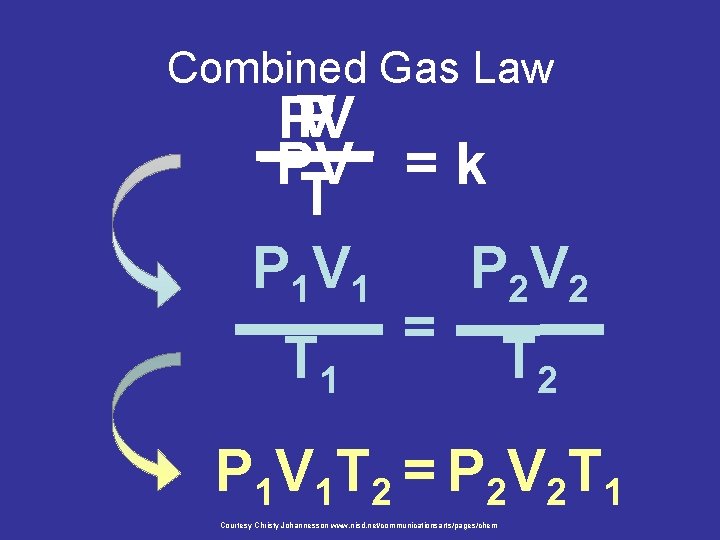
Combined Gas Law P V PV PV = k T P 1 V 1 P 2 V 2 = T 1 T 2 P 1 V 1 T 2 = P 2 V 2 T 1 Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

The Combined Gas Law A quantity of gas has a volume of 400 cm 3 at STP. What volume will it occupy at 35 o. C and 83. 3 k. Pa? (101. 325 k. Pa) x (400 cm 3) = (83. 3 k. Pa) x (V 2) 273 K P 1 = T 1 = V 1 = P 2 = T 2 = V 2 = 101. 325 k. Pa 273 K 400 cm 3 83. 3 k. Pa 35 o. C + 273 = 308 K ? cm 3 308 K V 2 = 548. 9 cm 3

The Combined Gas Law When measured at STP, a quantity of gas has a volume of 500 cm 3. What volume will it occupy at 20 o. C and 93. 3 k. Pa? (101. 325 k. Pa) x (500 cm 3) = (93. 3 k. Pa) x (V 2) 273 K P 1 = T 1 = V 1 = P 2 = T 2 = V 2 = 101. 325 k. Pa 273 K 500 cm 3 93. 3 k. Pa 20 o. C + 273 = 293 K ? cm 3 293 K V 2 = 582. 8 cm 3

Molar Volume (Avogadro) 1 mol of all gases @ STP have a volume of 22. 4 L Avogadro’s Law V 1/n 1 = V 2/n 2 Timberlake, Chemistry 7 th Edition, page 268

Ideal Gas Law PV = n. RT Brings together all gas properties. P = pressure V = volume (must be in liters) n = moles R = universal gas constant (0. 082 or 8. 314) T = temperature (must be in Kelvin) Can be derived from experiment and theory.

Ideal Gas Law What is the pressure of 0. 18 mol of a gas in a 1. 2 L flask at 298 K? PV = n. RT P x (1. 2 L) = (0. 18 mol) x (. 082) x (298 K) P = ? atm n = 0. 18 mol T = 298 K V = 1. 2 L R =. 082 (L x atm)/(mol x K) P = 3. 7 atm

Gas Density D = (MM)P/RT Larger particles are more dense. Gases are more dense at higher pressures and lower temperatures D = density P = pressure MM = molar mass R = universal gas constant T = temperature (must be in Kelvin) Can be derived from experiment and theory.

Gas Problems 1. The density of an unknown gas is 0. 010 g/ml. What is the molar mass of this gas measured at -11. 00 C and 3. 25 atm? Use proper sig figs. g/mol = (0. 010 g/ml) x (. 082 atm L/mol K) x (262 K) x (1/3. 25 atm) x (1000 ml/1 L) Molar mass = ? g/mol D = 0. 010 g/ml T = 262 K P = 3. 25 atm R =. 082 (L atm)/(mol K) P = 66 g/mol

Gas Problems 2. What is the volume of 3. 35 mol of gas which has a measured temperature of 47. 00 C and a pressure of 185 k. Pa? Use proper sig figs. (185 k. Pa) x (V) = (3. 35 mol) x (8. 314 L k. Pa/mol K) x (320 K) PV = n. RT V= ? L n = 3. 35 mol T = 320 K P = 185 k. Pa R = 8. 314 (L k. Pa)/(mol K) V = 48. 2 L

Dalton’s Law The total pressure of a mixture of gases equals the sum of the partial pressures of the individual gases. Ptotal = P 1 + P 2 +. . . In a gaseous mixture, a gas’s partial pressure is the one the gas would exert if it were by itself in the container. The mole ratio in a mixture of gases determines each gas’s partial pressure. Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

Gas Mixtures and Dalton’s Law

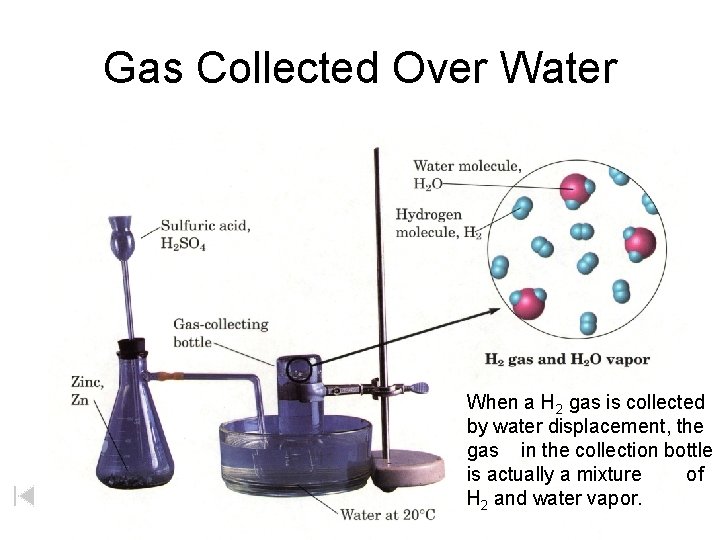
Gas Collected Over Water When a H 2 gas is collected by water displacement, the gas in the collection bottle is actually a mixture of H 2 and water vapor.

Dalton’s Law Hydrogen gas is collected over water at 22°C. Find the pressure of the dry gas if the atmospheric pressure is 94. 4 k. Pa. The total pressure in the collection bottle is equal to atmospheric pressure and is a mixture of H 2 and water vapor. GIVEN: P H 2 = ? Ptotal = 94. 4 k. Pa PH 2 O = 2. 6 k. Pa WORK: Ptotal = PH 2 + PH 2 O 94. 4 k. Pa = PH 2 + 2. 6 k. Pa PH 2 = 91. 8 k. Pa Look up water-vapor pressure on p. 10 for 22°C. Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

Dalton’s Law The total pressure of mixture (3. 0 mol He and 4. 0 mol Ne) is 97. 4 k. Pa. What is the partial pressure of each gas. PHe = 3 mol He (97. 4 k. Pa) = 41. 7 k. Pa 7 mol gas PNe = 4 mol Ne (97. 4 k. Pa) = 55. 7 k. Pa 7 mol gas

Dalton’s Law Suppose you are given four containers – three filled with noble gases. The first 1 L container is filled with argon and exerts a pressure of 2 atm. The second 3 liter container is filled with krypton and has a pressure of 380 mm Hg. The third 0. 5 L container is filled with xenon and has a pressure of 607. 8 k. Pa. If all these gases were transferred into an empty 2 L container…what would be the pressure in the “new” container? PKr = 380 mm Hg PAr = 2 atm V = 1 liter Pxe 607. 8 k. Pa V = 3 liters V = 0. 5 liter Ptotal = ? V = 2 liters

…just add them up PKr = 380 mm Hg PAr = 2 atm Ptotal = ? Pxe 607. 8 k. Pa V = 1 liter V = 3 liters V = 0. 5 liter V = 2 liters Dalton’s Law of Partial Pressures “Total Pressure = Sum of the Partial Pressures” PT = PAr + PKr + PXe + … P 1 x V 1 = P 2 x V 2 (0. 5 atm) (3 L) = (X atm) (2 L) PKr = 0. 75 atm P 1 x V 1 = P 2 x V 2 (6 atm) (0. 5 L) = (X atm) (2 L) Pxe = 1. 5 atm PT = 1 atm + 0. 75 atm + 1. 5 atm PT = 3. 25 atm

Partial Pressure A gas is collected over water at 649 torr and 26. 00 C. If its volume when collected is 2. 99 L, what is its volume at STP? Use proper sig figs. (83. 1 x 2. 99) / 299 = (101. 325 x V 2) / 273 P 1 V 1/T 1 = P 2 V 2/T 2 PT = P G + P w V 2 = ? L V 1 = 2. 99 L T 1 = 299 K T 2 = 273 K PT = 649 torr P 1 = 86. 5 k. Pa – 3. 4 k. Pa = 83. 1 k. Pa P 2 = 101. 325 k. Pa V 2 = 2. 24 L

Gas Stoichiometry Find the volume of hydrogen gas made when 38. 2 g zinc react with excess hydrochloric acid. Pressure =107. 3 k. Pa; temperature = 88 o. C. Zn (s) + 2 HCl (aq) Zn. Cl 2 (aq) + H 2 (g)

Gas Stoichiometry Find the volume of hydrogen gas made when 38. 2 g zinc react with excess hydrochloric acid. Pressure =107. 3 k. Pa; temperature = 88 o. C. Zn (s) + 2 HCl (aq) Zn. Cl 2 (aq) + H 2 (g) 38. 2 g excess At STP, we’d use 22. 4 L per mol, but we aren’t at STP. V = ? L H 2 P = 107. 3 k. Pa T = 88 o. C (361 K)

Pressure and Balloons B When balloon is being filled: PA > P B A When balloon is filled and tied: PA = P B When balloon deflates: PA < P B A = pressure exerted BY balloon B = pressure exerted ON balloon

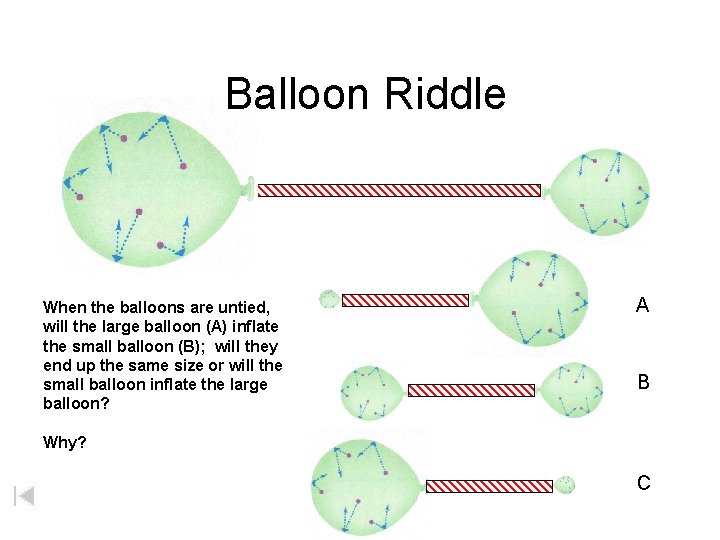
Balloon Riddle When the balloons are untied, will the large balloon (A) inflate the small balloon (B); will they end up the same size or will the small balloon inflate the large balloon? A B Why? C