KINETIC MOLECULAR THEORY AND THE GAS LAWS KINETIC

KINETIC MOLECULAR THEORY AND THE GAS LAWS

KINETIC MOLECULAR THEORY

Kinetic Molecular Theory Postulates of the Kinetic Molecular Theory of Gases 1. Gases consist of tiny particles (atoms or molecules) These particles are so small, compared with the distances between them, that the volume (size) of the individual particles can be assumed to be negligible (zero). 2. The particles are in constant random motion, colliding with the walls of the container. These collisions with the walls cause the pressure exerted by the gas. 3. Molecular collisions are elastic. This means that although individual molecules may gain or lose kinetic energy, there is no net (overall) gain or loss of kinetic energy from these collisions. 4. The average kinetic energy of the gas particles is directly proportional to the Kelvin temperature of the gas

KMT Postulate 1 Gases consist of tiny particles (atoms or molecules) These particles are so small, compared with the distances between them, that the volume (size) of the individual particles can be assumed to be negligible (zero). o o o

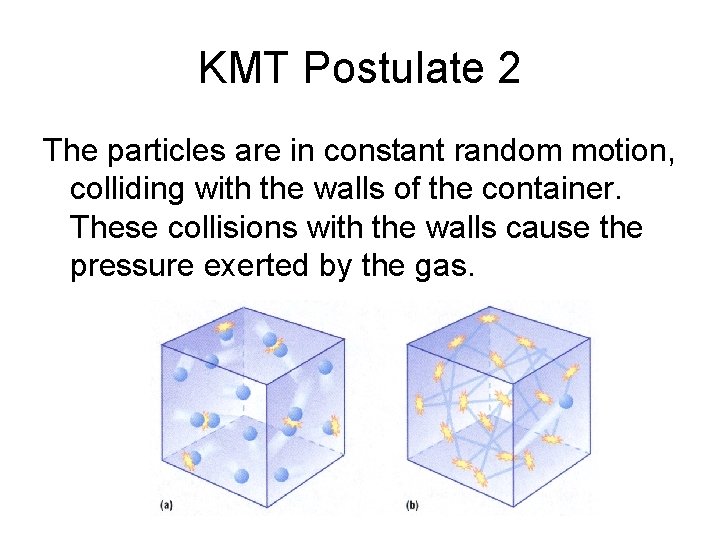
KMT Postulate 2 The particles are in constant random motion, colliding with the walls of the container. These collisions with the walls cause the pressure exerted by the gas.

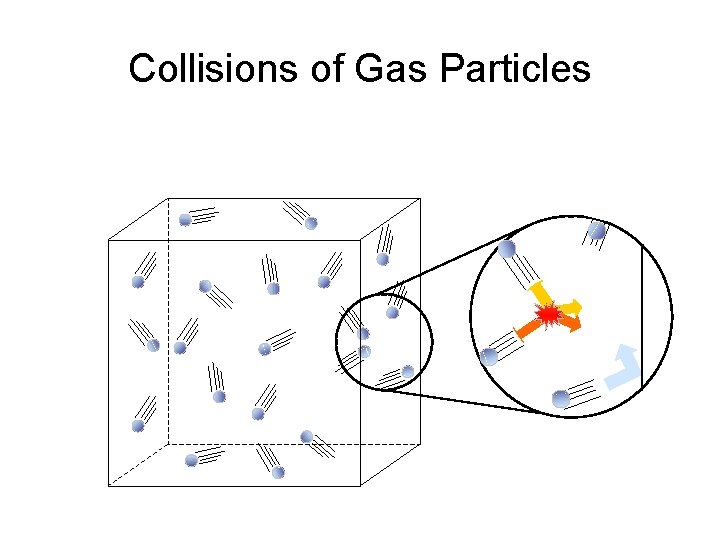
Collisions of Gas Particles

Kinetic Theory

KMT Postulate 3 Molecular collisions are elastic. This means that although individual molecules may gain or lose kinetic energy, there is no net (overall) gain or loss of kinetic energy from these collisions. - There are no attractive forces between molecules

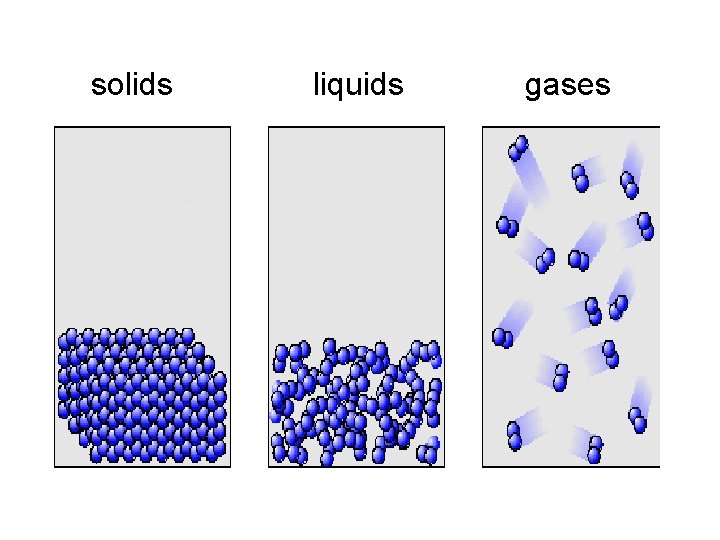
solids liquids gases

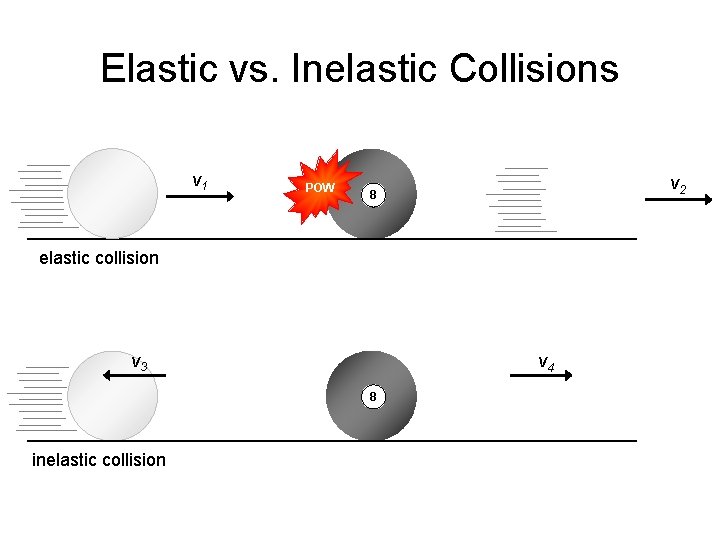
Elastic vs. Inelastic Collisions 8 3

Elastic vs. Inelastic Collisions v 1 POW v 2 8 elastic collision v 3 v 4 8 inelastic collision

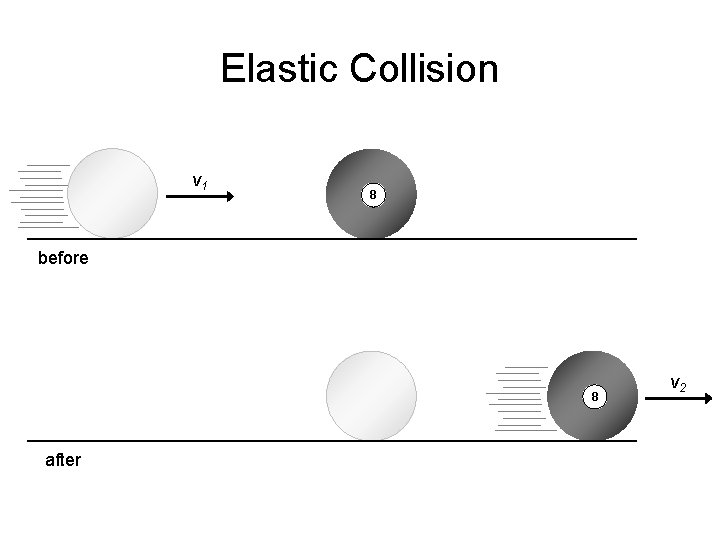
Elastic Collision v 1 8 before 8 after v 2

KMT Postulate 4 The average kinetic energy of the gas particles is directly proportional to the Kelvin temperature of the gas

Kinetic Molecular Theory (KMT) Ø explains why gases behave as they do Ø deals w/“ideal” gas particles… 1. …are so small that they are assumed to have zero volume 2. …are in constant, straight-line motion 3. …experience elastic collisions in which no energy is lost…have no attractive or repulsive forces toward each other 4. …have an average kinetic energy (KE) that is proportional to the absolute temp. of gas (i. e. , Kelvin temp. ) AS TEMP. , KE

VARIABLES OF GAS LAWS Volume Temperature Pressure Mole

VARIABLES OF GAS LAWS • Volume – three-dimensional space that matter occupies • Temperature - property of matter which reflects the quantity of kinetic energy of the component particles • Pressure – force exerted by particles on a specific area • Mole – the unit of counting molecules, atoms or any particle.

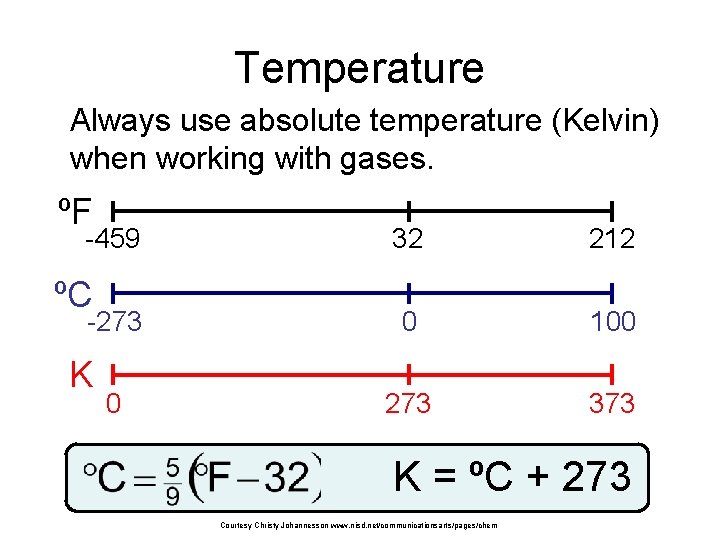
Temperature Always use absolute temperature (Kelvin) when working with gases. ºF -459 ºC -273 K 0 32 212 0 100 273 373 K = ºC + 273 Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

Pressure Which shoes create the most pressure? Courtesy Christy Johannesson www. nisd. net/communicationsarts/pages/chem

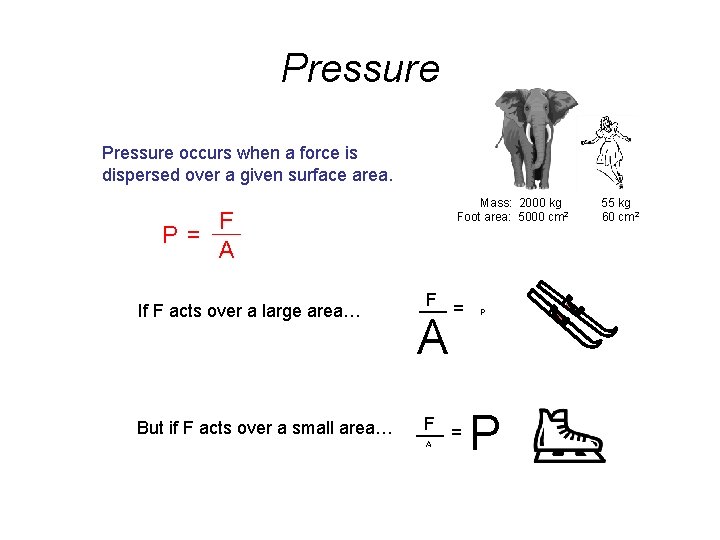
Pressure occurs when a force is dispersed over a given surface area. P= Mass: 2000 kg Foot area: 5000 cm 2 F A If F acts over a large area… But if F acts over a small area… F = A P P 55 kg 60 cm 2

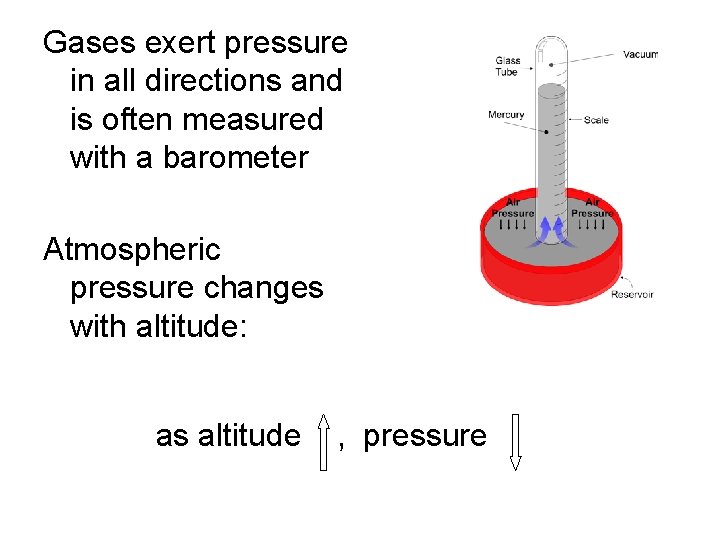
Gases exert pressure in all directions and is often measured with a barometer Atmospheric pressure changes with altitude: as altitude , pressure

Pressure and Temperature STP (Standard Temperature and Pressure) standard temperature 0 o. C 273 K standard pressure 1 atm 101. 3 k. Pa 760 mm Hg Equations / Conversion Factors: K = o. C + 273 o. C = K – 273 C = (5/9)*(F-32) F = (9/5)*C+32 1 atm = 101. 3 k. Pa = 760 mm Hg

Properties of Gases Gas properties can be modeled using math. Model depends on: V = volume of the gas (liters, L) T = temperature (Kelvin, K) P = pressure (atmospheres, atm, torr, k. Pa) n = amount (moles, mol)

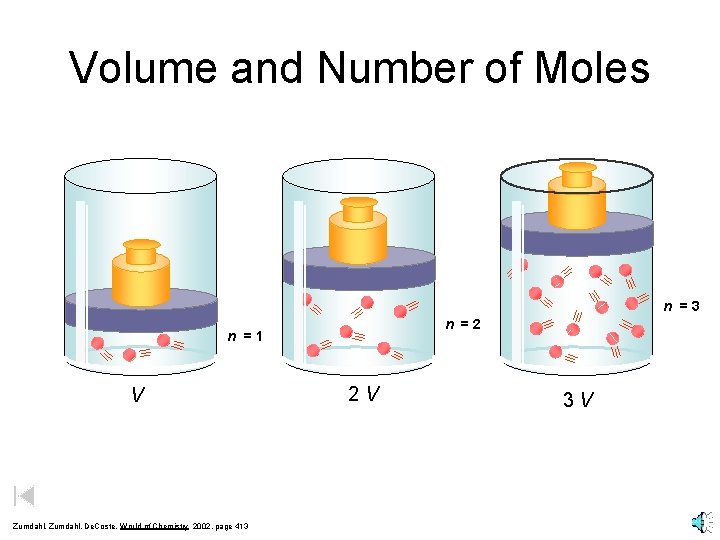
Volume and Number of Moles n =3 n =2 n =1 V Zumdahl, De. Coste, World of Chemistry 2002, page 413 2 V 3 V

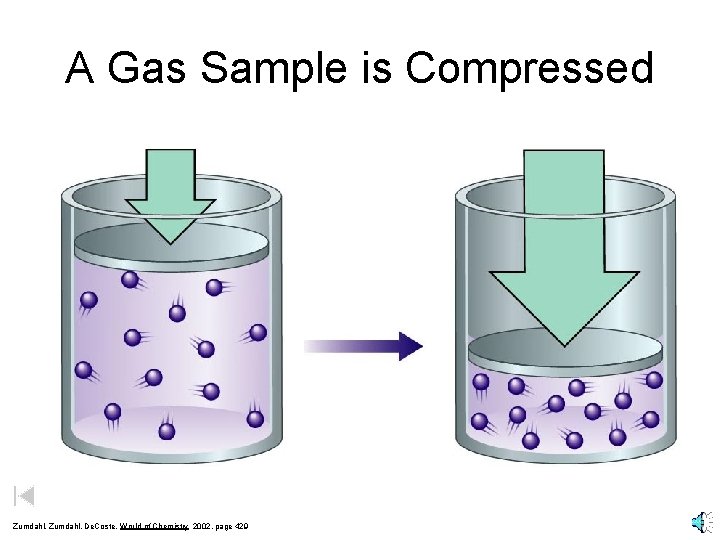
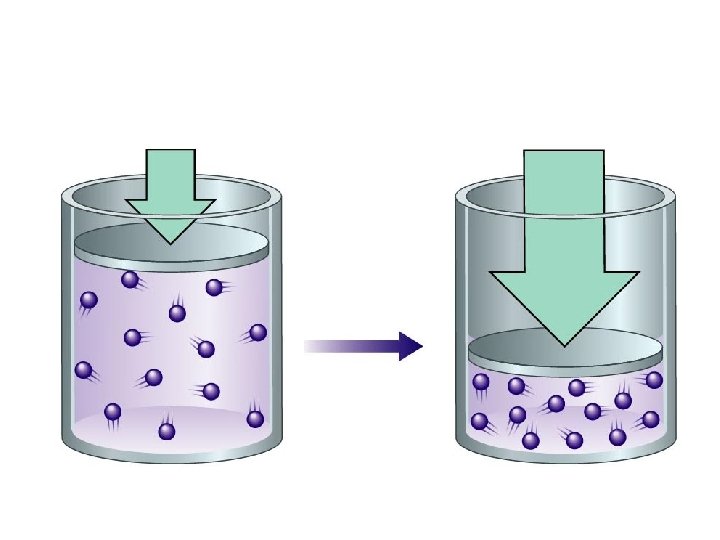
A Gas Sample is Compressed Zumdahl, De. Coste, World of Chemistry 2002, page 429

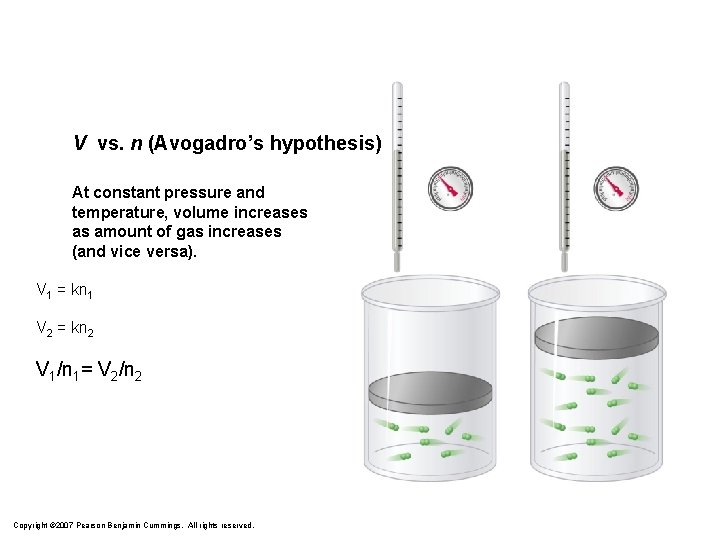
Avogadro's Hypothesis Equal volumes of gases at the same T and P have the same number of molecules. V = kn This means, for example, that number of moles goes up as volume goes up. V and n are directly related. *Amedeo Avogadro (1776 - 1856) twice as many molecules 1 mole = 6. 022 x 1023 *Lorenzo Romano Amedeo Carlo Avogadro, conte di Quaregna e Cerreto

Avogadro’s Hypothesis N 2 H 2 Ar CH 4 At the same temperature and pressure, equal volumes of different gases contain the same number of molecules. Each balloon holds 1. 0 L of gas at 20 o. C and 1 atm pressure. Each contains 0. 045 mol or 2. 69 x 1022 molecules of gas.

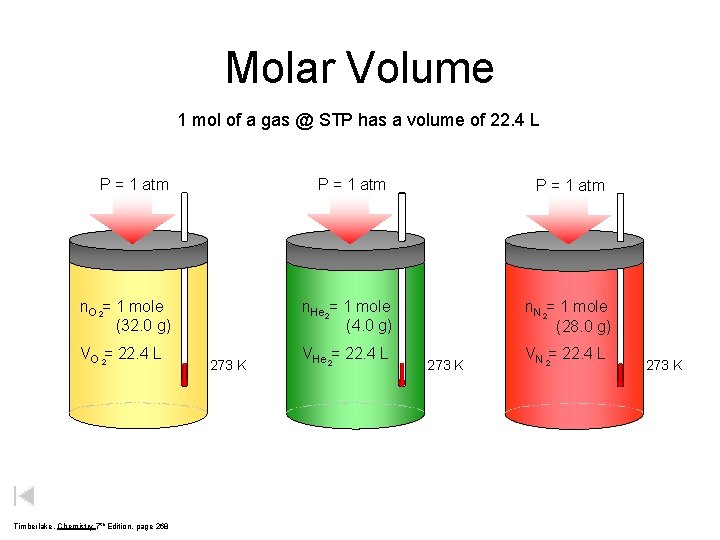
Molar Volume 1 mol of a gas @ STP has a volume of 22. 4 L P = 1 atm n. O 2= 1 mole (32. 0 g) VO 2= 22. 4 L Timberlake, Chemistry 7 th Edition, page 268 273 K P = 1 atm n. He 2= 1 mole (4. 0 g) n. N 2= 1 mole (28. 0 g) VHe 2= 22. 4 L 273 K VN 2= 22. 4 L 273 K

V vs. n (Avogadro’s hypothesis) At constant pressure and temperature, volume increases as amount of gas increases (and vice versa). V 1 = kn 1 V 2 = kn 2 V 1/n 1= V 2/n 2 Copyright © 2007 Pearson Benjamin Cummings. All rights reserved.

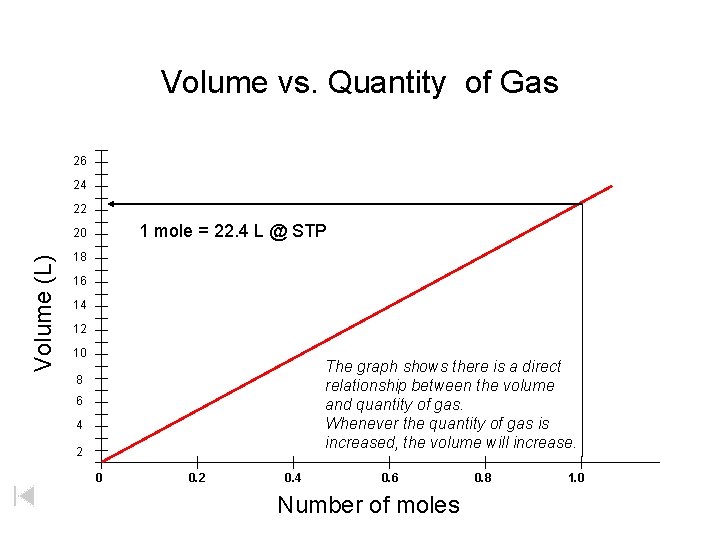
Volume vs. Quantity of Gas 26 24 22 1 mole = 22. 4 L @ STP Volume (L) 20 18 16 14 12 10 The graph shows there is a direct relationship between the volume and quantity of gas. Whenever the quantity of gas is increased, the volume will increase. 8 6 4 2 0 0. 2 0. 4 0. 6 Number of moles 0. 8 1. 0

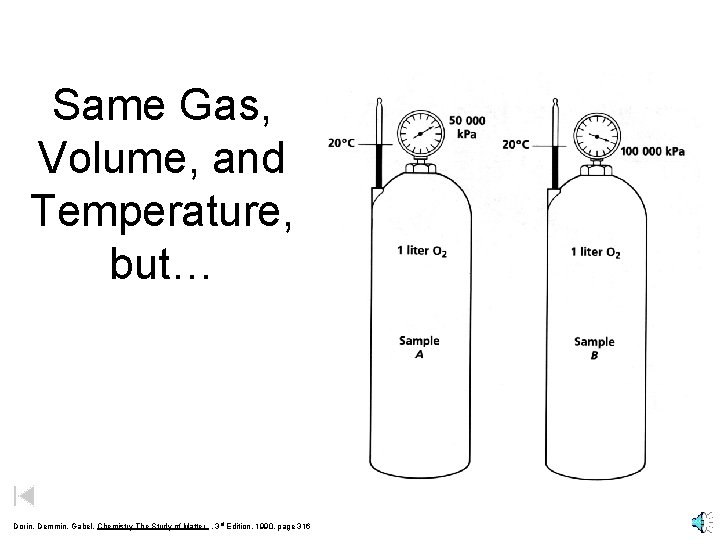
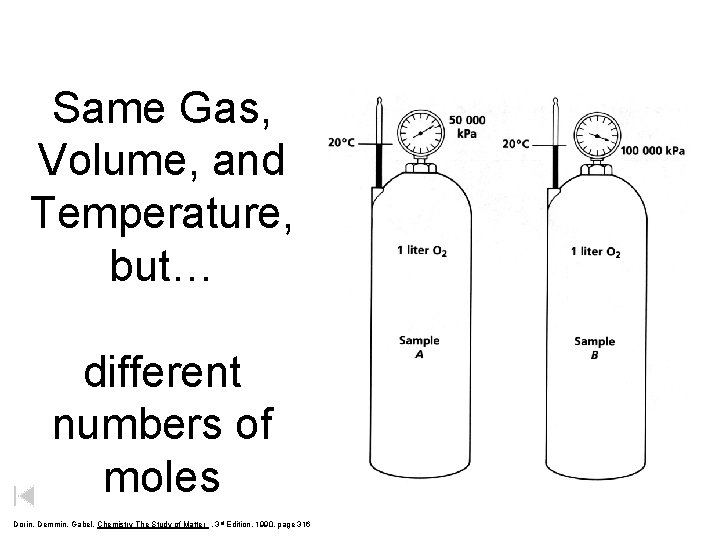
Same Gas, Volume, and Temperature, but… Dorin, Demmin, Gabel, Chemistry The Study of Matter , 3 rd Edition, 1990, page 316

Same Gas, Volume, and Temperature, but… different numbers of moles Dorin, Demmin, Gabel, Chemistry The Study of Matter , 3 rd Edition, 1990, page 316

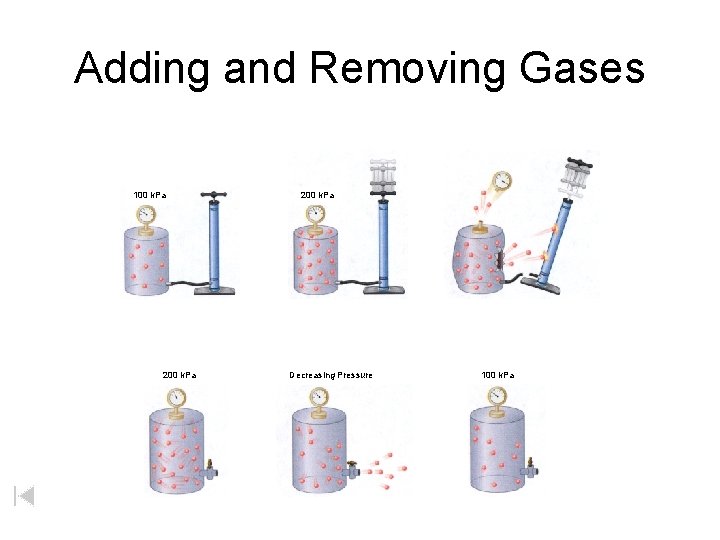
Adding and Removing Gases 100 k. Pa 200 k. Pa Decreasing Pressure 100 k. Pa

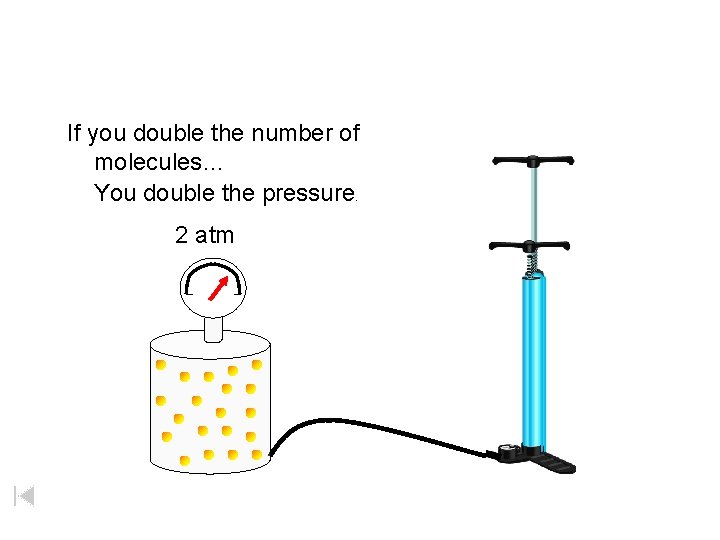
If you double the number of molecules 1 atm http: //www. tvgreen. com/chapt 14/Chapt 14. ppt#262, 8, Slide 8

If you double the number of molecules… You double the pressure. 2 atm

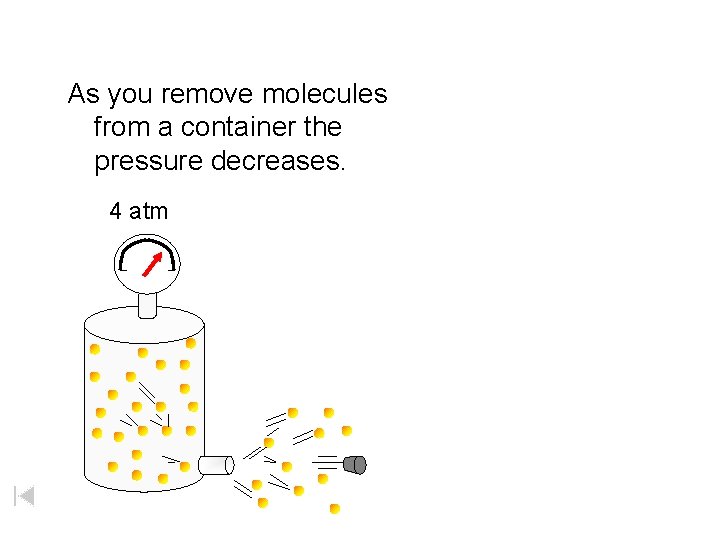
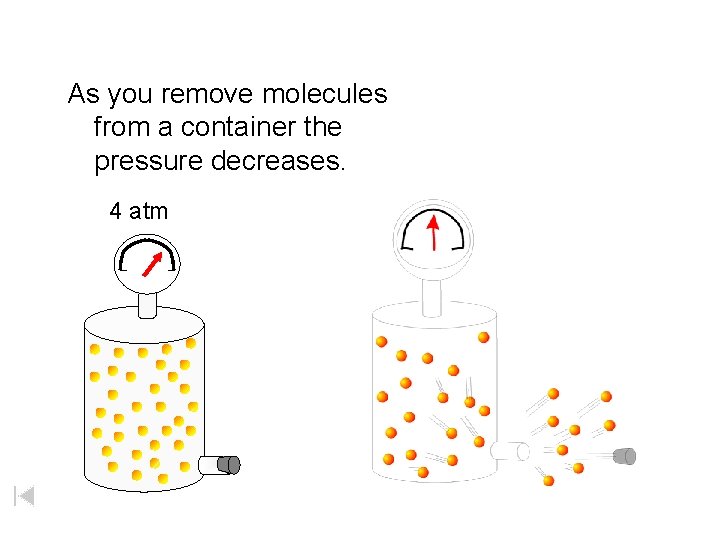
As you remove molecules from a container the pressure decreases. 4 atm

As you remove molecules from a container the pressure decreases. 4 atm

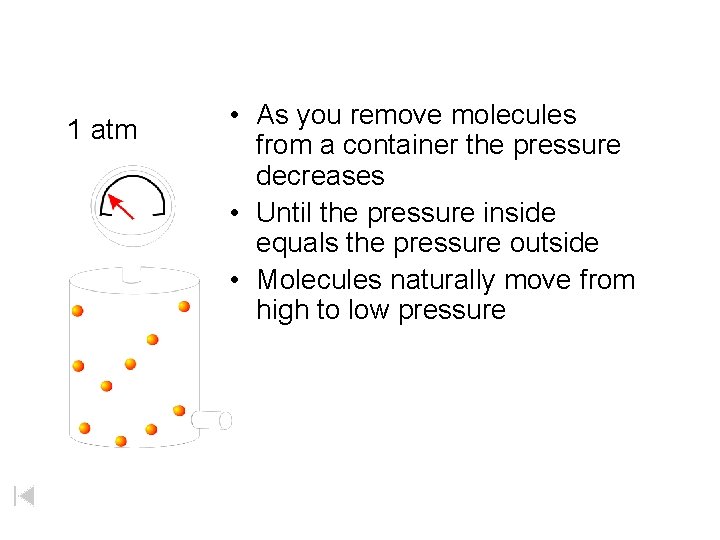
1 atm • As you remove molecules from a container the pressure decreases • Until the pressure inside equals the pressure outside • Molecules naturally move from high to low pressure

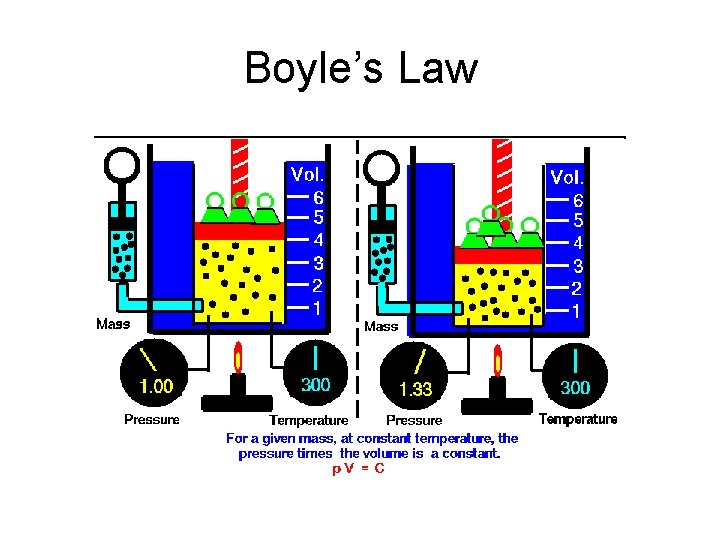
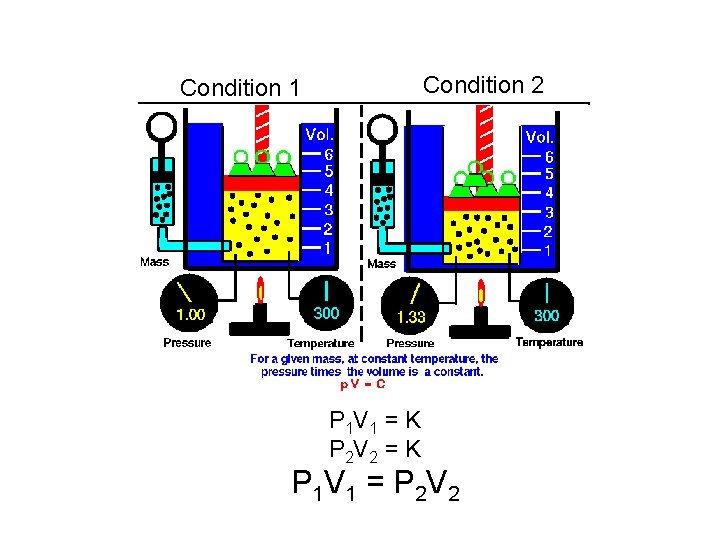
Boyle’s Law

Boyle’s Law At a constant temperature, the product of the pressure and the volume of a gas sample is a constant value.

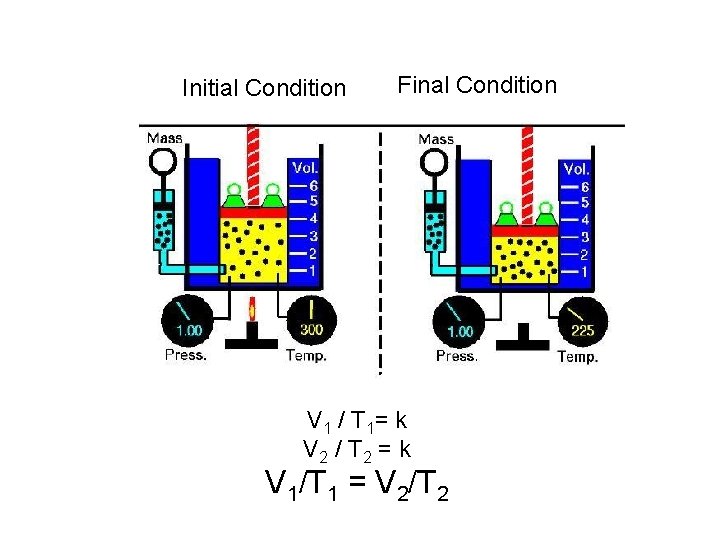
Condition 2 Condition 1 P 1 V 1 = K P 2 V 2 = K P 1 V 1 = P 2 V 2

Problem Solving If 35 m. L of oxygen gas is compressed from 1, 900 torr pressure to 1. 8 atm pressure, what is the new volume at constant temperature?

Step 1: Identify the variables (Given) Given: Initial Conditions P 1 = 1, 900 torr V 1 = 35 m. L Convert to uniform units 1. 8 atm x 760 torr = 1 atm Final Conditions P 2 = 1. 8 atm V 2 = ? 1368 torr

Step 2: Identify what is Required and state the appropriate equation Required: The volume at the final condition (V 2) Equation: From Boyle’s Law, P 1 V 1 = P 2 V 2 = P 1 V 1 P 2

Step 3: Substitute and do the Math Solution: V 2 = P 1 V 1 P 2 = 1900 torr (35 m. L) 1368 torr Answer: 49 m. L of oxygen = 48. 6111111 ml

Your Turn • Where is this principle applicable? Explain.

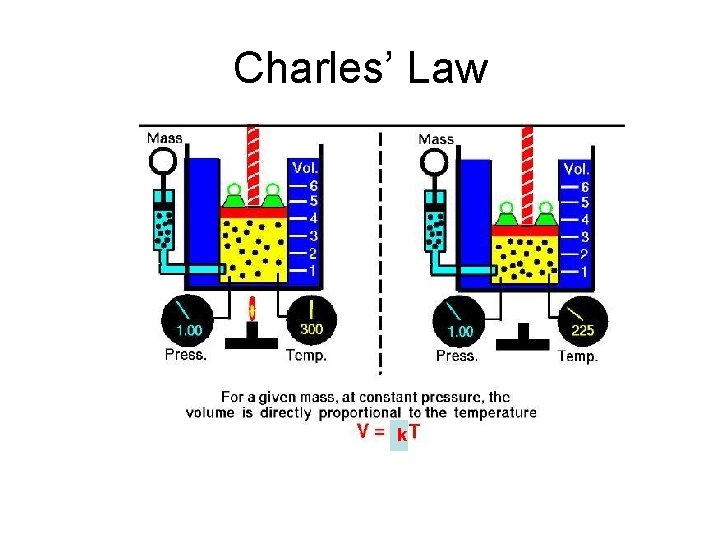
Charles’ Law k

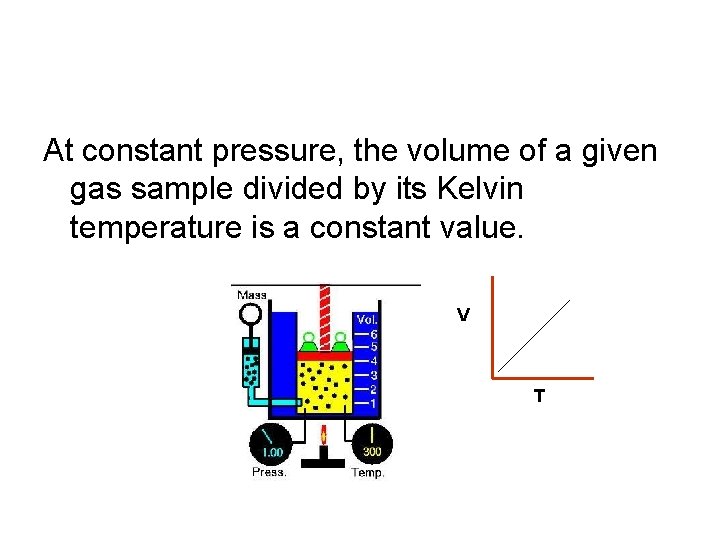
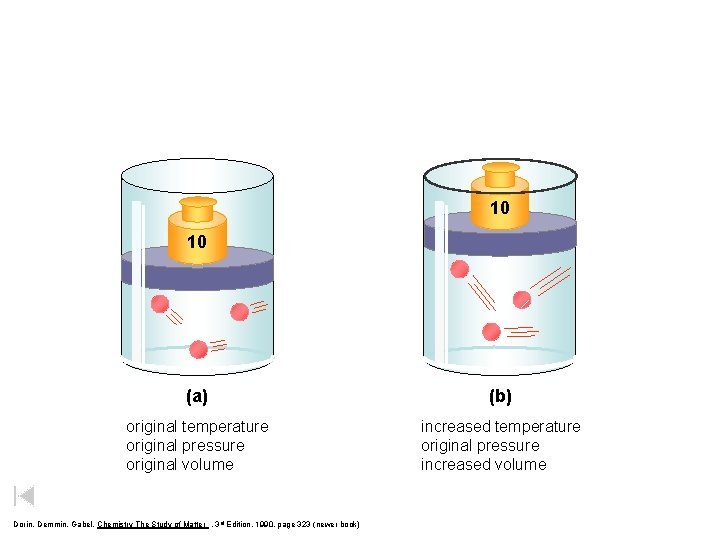
At constant pressure, the volume of a given gas sample divided by its Kelvin temperature is a constant value. V T

10 10 (a) (b) original temperature original pressure original volume increased temperature original pressure increased volume Dorin, Demmin, Gabel, Chemistry The Study of Matter , 3 rd Edition, 1990, page 323 (newer book)

Initial Condition Final Condition V 1 / T 1= k V 2 / T 2 = k V 1/T 1 = V 2/T 2

Problem Solving If the temperature of a 12 L gas sample increases from 32 C to 60 C, what will happen to the volume of the gas?

Step 1: Identify the variables (Given) Given: Initial Conditions T 1 = 32 C V 1 = 12 L Convert to standard units T 1 = 32 C + 273 = 305 K T 2 = 60 C + 273 = 333 K Final Conditions T 2 = 60 C V 2 = ?

Step 2: Identify what is Required and state the appropriate equation Required: The volume at the final condition (V 2) Equation: From Charles’ Law, V 1/T 1 = V 2/T 2 V 2 = T 2 V 1 T 1

Step 3: Substitute and do the Math Solution: V 2 = T 2 V 1 T 1 = 333 K (12 L) 305 K Answer: 13 L = 13. 1016393442 L

Your Turn • Where is this principle applicable? Explain.

Gay Lussac’s Law

• At constant volume, the pressure of a given gas sample divided by its Kelvin temperature is a constant value • V 1/T 1= k P • V 1/T 1= V 2/T 2 T

Problem Solving • 10. 0 L of a gas is found to exert 97. 0 k. Pa at 25. 0°C. What would be the required temperature (in celcius) to change the pressure to standard pressure?

Step 1: Identify the variables (Given) Given: Initial Conditions T 1 = 25. 0°C P 1 = 97. 0 k. Pa Convert to standard units T 1 = 25 C + 273 = 298 K Final Conditions T 2 = ? P 2 = 101. 3 k. Pa

Gas Stoich • Because 1 mol of any gas at STP occupies 22. 4 L we can now solve for the volume of a gas in a reaction using stoich. • Refer to pp 141 of packet.