Kinetic Model of Gases Section 1 9 1

Kinetic Model of Gases Section 1. 9, 1. 11

Assumptions l l l A gas consists of molecules in ceaseless random motion The size of the molecules is negligible in the sense that their diameters are much smaller than the average distance traveled between collisions The molecules do not interact, except during collisions

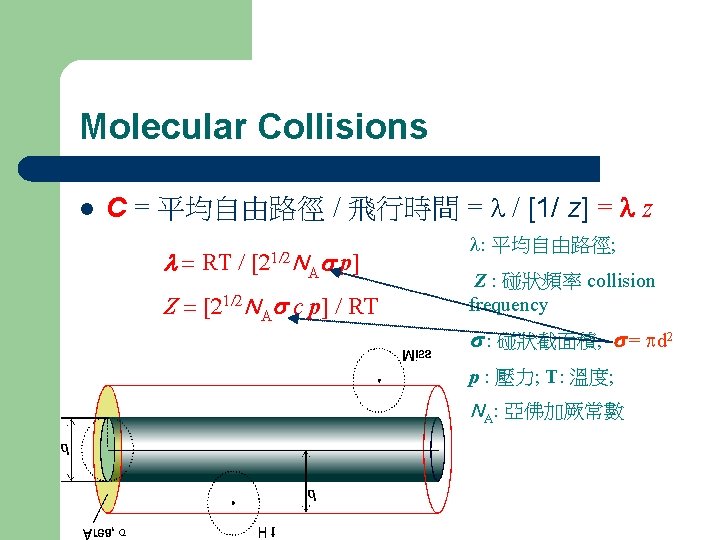
Pressure of a gas l l M molecular weight; V volume c root-mean-square speed (rms speed)

Speed of gases l r. m. s. speed l mean speed

Average speed of gas molecules • Effect of Molecular Weight • Temperature Effect

Kinetic Energy of Molecules l Ek = 3/2 RT Ek kinetic energy; T temperature; R gas constant l The average kinetic energy per molecule k. B Boltzmann constant = R/6. 02 1023

Partial Pressure l. Dalton’s Law The total pressure observed for a mixture of gases is equal to the sum of the pressures that each individual component gas would exert Ptotal = P 1+P 2+P 3+…+PJ PJ = x. J Ptotal pressure; PJ partial pressure of component J; c. J molar fraction of component J.

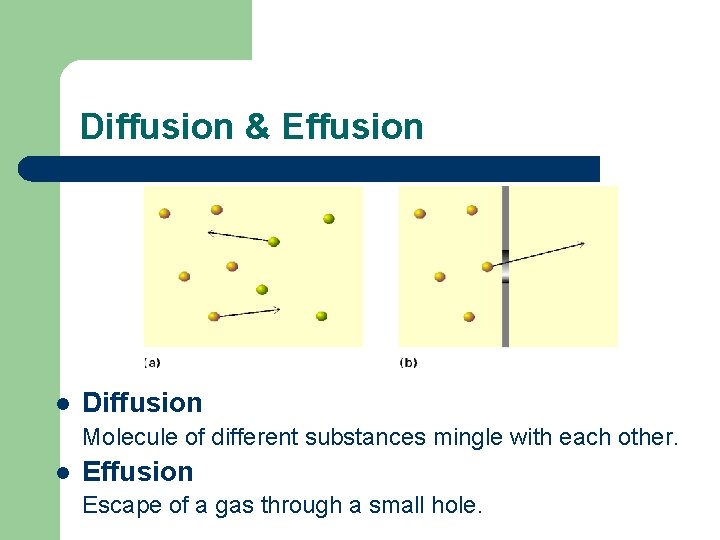
Diffusion & Effusion l Diffusion Molecule of different substances mingle with each other. l Effusion Escape of a gas through a small hole.

Diffusion & Effusion l Rates of diffusion and effusion of gases increase with increasing temperature. l For effusion the rate decreases with increasing molar mass.

Diffusion & Effusion l Graham’s Law At a given pressure and temperature, the rate of effusion of a gas is inversely proportional to the square root of its molar mass.

Diffusion & Effusion l The rate at which hydrogen and carbon dioxide effuse under the same conditions of pressure and temperature are in the ratio

Diffusion & Effusion l Separation of uranium-235 from uranium-238, in the form of volatile solids UF 6 http: //www. columbia. edu/itc/chemistry/chem-c 1403/text_chapters/nukes. html http: //www. uic. com. au/uicchem. htm http: //www. uilondon. org/index. htm

Effusion as a separation technique Use porous membranes to separate light gases from heavy ones l average speed of gas molecules depends on the masses of their molecules l heavy molecules in a mixture move slower on average than light ones l gases made of light molecules diffuse through pores in membranes faster than heavy molecules Differences from dialysis l membrane is permeable, not semipermeable: all gas molecules in the mixture can pass through it l size of molecules isn't usually important: pores in membrane are much larger than gas molecules l. . . molecular velocity (and so, molecular mass) is the basis for separation, not size Examples l separating helium from oxygen l separating uranium isotopes as volatile UF 6

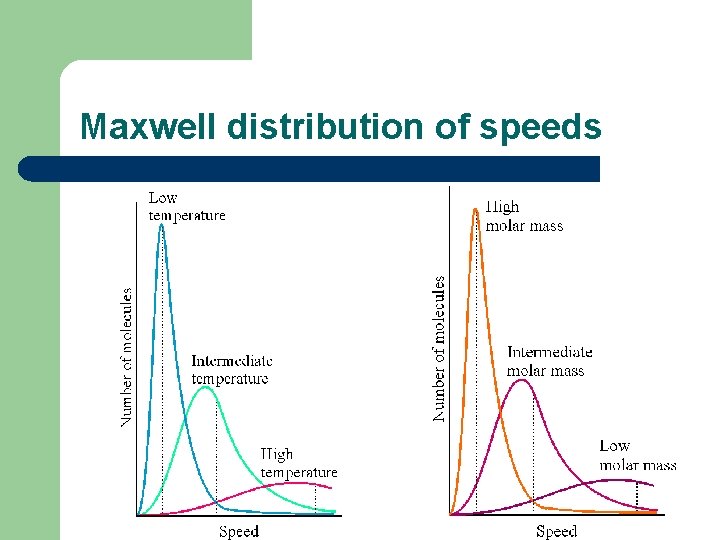
Maxwell distribution of speeds The Maxwell distribution of speeds f = F (s) DS F (s) = 4 p[m / 2 pk. B T](3/2) s 2 2/2 k. BT) -(ms e f : 運動速率在某個範圍內的分子之比例 s: 分子運動速率 speed; Ds : 速率的範圍 interval of speed KB : Boltzmann Constant

Maxwell distribution of speeds f = F (s) DS F (s) = 4 p[m/ 2 pk. B T](3/2) s 2 2/2 k. BT) -(ms e f DS 當設定的速率範圍增大時, 所含蓋的分子比例也隨之增加

Maxwell distribution of speeds f = F (s) DS F (s) = 4 p[m / 2 pk. B T](3/2) s 2 4 p[m / 2 pk. BT](3/2) 使分子比例的呈現在 0與1之間 2/2 k. BT) -(ms e

Maxwell distribution of speeds

Distribution of Translational Energy l Maxwell-Boltzmann Distribution Law f = F (e) De F (e) = 2 p / (pk. BT)(3/2) e 1/2 e-(e/k. BT) l e kinetic energy (=1/2 mu 2)